2025苏教版高中数学选择性必修第二册强化练习题(含解析)--6.1.1 空间向量的线性运算
文档属性
| 名称 | 2025苏教版高中数学选择性必修第二册强化练习题(含解析)--6.1.1 空间向量的线性运算 |

|
|
| 格式 | docx | ||
| 文件大小 | 391.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-15 16:27:05 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025苏教版高中数学选择性必修第二册
第6章 空间向量与立体几何
6.1 空间向量及其运算
6.1.1 空间向量的线性运算
基础过关练
题组一 空间向量的概念与表示
1.(2024河北邢台期末)在长方体ABCD-A1B1C1D1中,下列向量与是相等向量的是( )
A.
2.(2024黑龙江哈尔滨第一中学期中)下列关于空间向量的说法中正确的是( )
A.方向相反的两个向量是相反向量
B.空间中任意两个单位向量必相等
C.若||满足||,则
D.相等向量其方向必相同
题组二 空间向量的加减运算
3.(2024江苏扬州中学期中)在空间四边形OABC中,=( )
A.
4.(2023江苏徐州期中)如图,在平行六面体ABCD-A'B'C'D'中,设=a,=b,=c,则下列各式的运算结果为的是( )
A.-a+b+c B.a-b+c
C.a-b-c D.a+b-c
题组三 空间向量的数乘运算
5.(2023江苏南京第一中学期末)在三棱柱ABC-A1B1C1中,M为A1C1的中点,若=a,=b,=c,则=( )
A.-a+b+c B.a+b+c
C.-a-b+c D.a-b+c
6.(教材习题改编)如图,在平行六面体ABCD-A1B1C1D1中,点M在BB1上,点N在DD1上,且BM=D1D,若,则x+y+z=( )
A.
7.(2023江苏扬州宝应期中)已知在四面体OABC中,E为OA的中点,,若=a,=b,=c,则=( )
A.a-b-c B.-a-b+c
C.-a+b+c D.-a+b+c
题组四 共线向量定理
8.(2024江苏南京六校联合体期中)已知向量e1,e2是平面上两个不共线的单位向量,且=e1+2e2,=-3e1+2e2,=3e1-6e2,则( )
A.A,B,C三点共线 B.A,B,D三点共线
C.A,C,D三点共线 D.B,C,D三点共线
9.(2024贵州“三新”改革联盟联考)已知在三棱柱ABC-A1B1C1中,P为空间一点,且满足,λ,μ∈[0,1],则下列说法错误的是( )
A.当λ=0时,点P在棱BB1上
B.当λ=μ时,点P在线段B1C上
C.当μ=1时,点P在棱B1C1上
D.当λ+μ=1时,点P在线段B1C上
能力提升练
题组一 空间向量的线性运算
1.(2024河北邯郸五校二调)在四面体ABCD中,点E满足(λ∈R),F为BE的中点,且,则λ=( )
A.
2.(2024四川雅安联考)如图,在四面体ABCD中,E,F分别为BC,AE的中点,G为△ACD的重心,则=( )
A.-
B.-
C.
D.
3.(2023江苏盐城响水中学期中)如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,点E在侧棱PC上,且PE=EC,若=a,=b,=c,则=( )
A.-a-b-c B.a+b+c
C.a+b+c D.-a-b-c
题组二 共线向量的判定与应用
4.(2024江苏无锡市北高级中学期初)已知A,B,C三点共线,则对空间任一点O,存在3个均不为0的实数λ,m,n,使λ=0,那么λ+m+n的值为 .
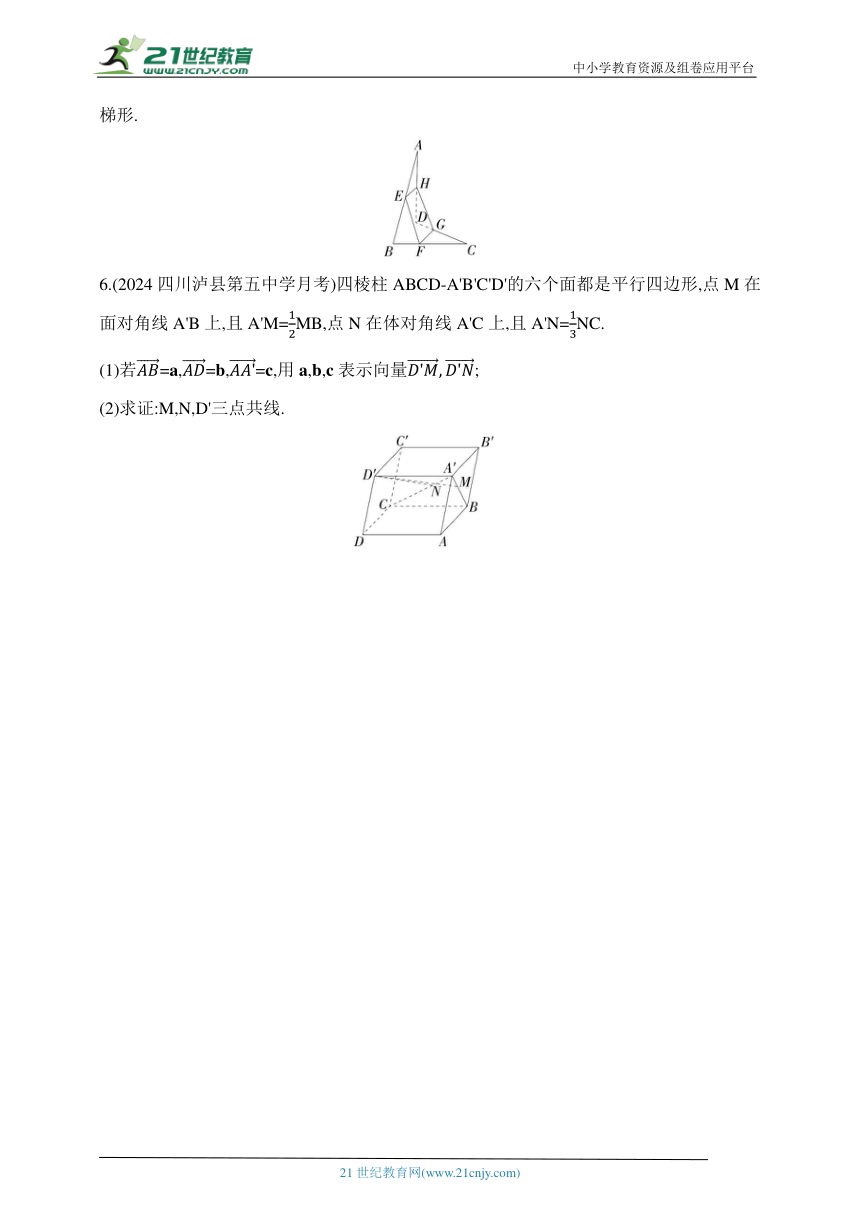
5.(2023河南洛阳新安第一高级中学月考)如图,已知空间四边形ABCD,E,H分别是AB,AD的中点,F,G分别是CB,CD上的点,且.用向量法求证:四边形EFGH是梯形.
6.(2024四川泸县第五中学月考)四棱柱ABCD-A'B'C'D'的六个面都是平行四边形,点M在面对角线A'B上,且A'M=MB,点N在体对角线A'C上,且A'N=NC.
(1)若=a,=b,=c,用a,b,c表示向量;
(2)求证:M,N,D'三点共线.
答案与分层梯度式解析
第6章 空间向量与立体几何
6.1 空间向量及其运算
6.1.1 空间向量的线性运算
基础过关练
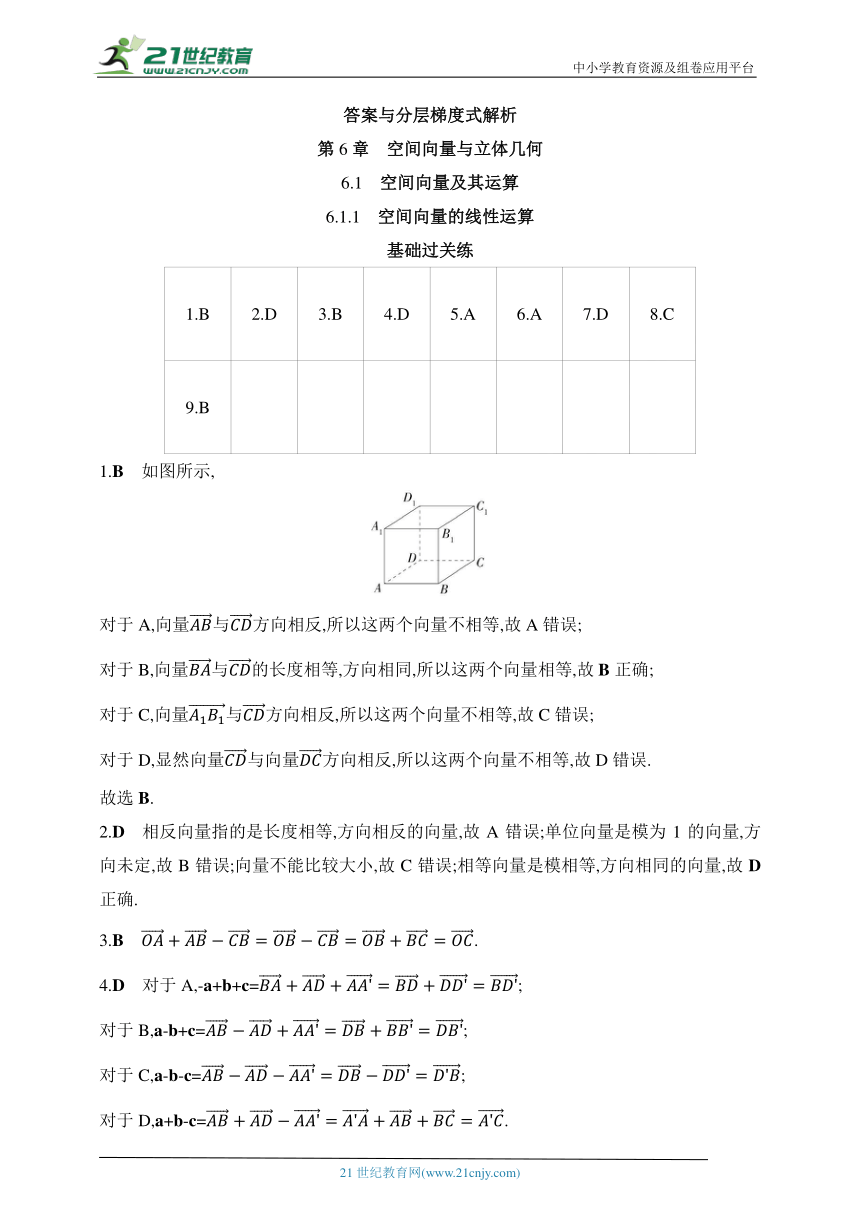
1.B 2.D 3.B 4.D 5.A 6.A 7.D 8.C
9.B
1.B 如图所示,
对于A,向量方向相反,所以这两个向量不相等,故A错误;
对于B,向量的长度相等,方向相同,所以这两个向量相等,故B正确;
对于C,向量方向相反,所以这两个向量不相等,故C错误;
对于D,显然向量方向相反,所以这两个向量不相等,故D错误.
故选B.
2.D 相反向量指的是长度相等,方向相反的向量,故A错误;单位向量是模为1的向量,方向未定,故B错误;向量不能比较大小,故C错误;相等向量是模相等,方向相同的向量,故D正确.
3.B .
4.D 对于A,-a+b+c=;
对于B,a-b+c=;
对于C,a-b-c=;
对于D,a+b-c=.
故选D.
5.A 如图,a+b+c.故选A.
6.A 由题意得,
又,所以x=-1,y=1,z=,所以x+y+z=.故选A.
7.D 如图所示,
解法一:由题意得=b+a=b+a=b+(c-b)-a=-a+b+c.故选D.
解法二:由题意得a+b+c.故选D.
方法总结 对于爪形图线段中的分点问题,常用的结论如下:如图,在△ABC中,D是线段BC上一点(不含端点),且,则.
8.C 对于A,若A,B,C三点共线,则存在唯一的实数λ,使得,即e1+2e2=λ(-3e1+2e2),则无解,所以A,B,C三点不共线,故A错误;
对于B,若A,B,D三点共线,则存在唯一的实数μ,使得,即e1+2e2=μ(3e1-6e2),则无解,所以A,B,D三点不共线,故B错误;
对于C,易得=(e1+2e2)+(-3e1+2e2)=-2e1+4e2=,且AC,AD有公共点A,所以A,C,D三点共线,故C正确;
对于D,易得=(3e1-6e2)+(e1+2e2)=4e1-4e2,若B,C,D三点共线,则存在唯一的实数k,使得,即4e1-4e2=k(-3e1+2e2),则无解,所以B,C,D三点不共线,故D错误.故选C.
9.B 对于A,当λ=0时,,所以,又μ∈[0,1],所以点P在棱BB1上,故A中说法正确;
对于B,当λ=μ时,),即,故,又λ∈[0,1],所以点P在线段BC1上,故B中说法错误;
对于C,当μ=1时,,所以λ,即,故,又λ∈[0,1],所以点P在棱B1C1上,故C中说法正确;
对于D,当λ+μ=1时,,即,即,故,又λ∈[0,1],所以点P在线段B1C上,故D中说法正确.
故选B.
能力提升练
1.D 2.B 3.B
1.D 因为F为BE的中点,所以,
又,所以.
由,得),即,所以λ=.故选D.
2.B 因为E,F分别为BC,AE的中点,所以).
因为G为△ACD的重心,所以),
所以.故选B.
知识总结 若G为△ABC的重心,则).
3.B 在△PAE中,,
∵PE=EC,
∴PE=PC,即,
又=a+b-c,
∴=c+(a+b-c)=a+b+c.
故选B.
4.答案 0
解析 因为A,B,C三点共线,所以存在唯一的实数k使,显然k≠0且k≠1,否则点A,B重合或点B,C重合,故),整理得(k-1)=0,又λ=0,所以λ=k-1,m=1,n=-k,显然实数λ,m,n均不为0,所以λ+m+n的值为0.
5.证明 连接BD.∵E,H分别是AB,AD的中点,且,
∴,
∴,且||≠||.
又F不在EH上,∴四边形EFGH是梯形.
6.解析 (1)∵A'M=,
∴a-b-c.
∵A'N=),
∴a-b-c.
(2)证明:∵,且,
∴,即M,N,D'三点共线.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025苏教版高中数学选择性必修第二册
第6章 空间向量与立体几何
6.1 空间向量及其运算
6.1.1 空间向量的线性运算
基础过关练
题组一 空间向量的概念与表示
1.(2024河北邢台期末)在长方体ABCD-A1B1C1D1中,下列向量与是相等向量的是( )
A.
2.(2024黑龙江哈尔滨第一中学期中)下列关于空间向量的说法中正确的是( )
A.方向相反的两个向量是相反向量
B.空间中任意两个单位向量必相等
C.若||满足||,则
D.相等向量其方向必相同
题组二 空间向量的加减运算
3.(2024江苏扬州中学期中)在空间四边形OABC中,=( )
A.
4.(2023江苏徐州期中)如图,在平行六面体ABCD-A'B'C'D'中,设=a,=b,=c,则下列各式的运算结果为的是( )
A.-a+b+c B.a-b+c
C.a-b-c D.a+b-c
题组三 空间向量的数乘运算
5.(2023江苏南京第一中学期末)在三棱柱ABC-A1B1C1中,M为A1C1的中点,若=a,=b,=c,则=( )
A.-a+b+c B.a+b+c
C.-a-b+c D.a-b+c
6.(教材习题改编)如图,在平行六面体ABCD-A1B1C1D1中,点M在BB1上,点N在DD1上,且BM=D1D,若,则x+y+z=( )
A.
7.(2023江苏扬州宝应期中)已知在四面体OABC中,E为OA的中点,,若=a,=b,=c,则=( )
A.a-b-c B.-a-b+c
C.-a+b+c D.-a+b+c
题组四 共线向量定理
8.(2024江苏南京六校联合体期中)已知向量e1,e2是平面上两个不共线的单位向量,且=e1+2e2,=-3e1+2e2,=3e1-6e2,则( )
A.A,B,C三点共线 B.A,B,D三点共线
C.A,C,D三点共线 D.B,C,D三点共线
9.(2024贵州“三新”改革联盟联考)已知在三棱柱ABC-A1B1C1中,P为空间一点,且满足,λ,μ∈[0,1],则下列说法错误的是( )
A.当λ=0时,点P在棱BB1上
B.当λ=μ时,点P在线段B1C上
C.当μ=1时,点P在棱B1C1上
D.当λ+μ=1时,点P在线段B1C上
能力提升练
题组一 空间向量的线性运算
1.(2024河北邯郸五校二调)在四面体ABCD中,点E满足(λ∈R),F为BE的中点,且,则λ=( )
A.
2.(2024四川雅安联考)如图,在四面体ABCD中,E,F分别为BC,AE的中点,G为△ACD的重心,则=( )
A.-
B.-
C.
D.
3.(2023江苏盐城响水中学期中)如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,点E在侧棱PC上,且PE=EC,若=a,=b,=c,则=( )
A.-a-b-c B.a+b+c
C.a+b+c D.-a-b-c
题组二 共线向量的判定与应用
4.(2024江苏无锡市北高级中学期初)已知A,B,C三点共线,则对空间任一点O,存在3个均不为0的实数λ,m,n,使λ=0,那么λ+m+n的值为 .
5.(2023河南洛阳新安第一高级中学月考)如图,已知空间四边形ABCD,E,H分别是AB,AD的中点,F,G分别是CB,CD上的点,且.用向量法求证:四边形EFGH是梯形.
6.(2024四川泸县第五中学月考)四棱柱ABCD-A'B'C'D'的六个面都是平行四边形,点M在面对角线A'B上,且A'M=MB,点N在体对角线A'C上,且A'N=NC.
(1)若=a,=b,=c,用a,b,c表示向量;
(2)求证:M,N,D'三点共线.
答案与分层梯度式解析
第6章 空间向量与立体几何
6.1 空间向量及其运算
6.1.1 空间向量的线性运算
基础过关练
1.B 2.D 3.B 4.D 5.A 6.A 7.D 8.C
9.B
1.B 如图所示,
对于A,向量方向相反,所以这两个向量不相等,故A错误;
对于B,向量的长度相等,方向相同,所以这两个向量相等,故B正确;
对于C,向量方向相反,所以这两个向量不相等,故C错误;
对于D,显然向量方向相反,所以这两个向量不相等,故D错误.
故选B.
2.D 相反向量指的是长度相等,方向相反的向量,故A错误;单位向量是模为1的向量,方向未定,故B错误;向量不能比较大小,故C错误;相等向量是模相等,方向相同的向量,故D正确.
3.B .
4.D 对于A,-a+b+c=;
对于B,a-b+c=;
对于C,a-b-c=;
对于D,a+b-c=.
故选D.
5.A 如图,a+b+c.故选A.
6.A 由题意得,
又,所以x=-1,y=1,z=,所以x+y+z=.故选A.
7.D 如图所示,
解法一:由题意得=b+a=b+a=b+(c-b)-a=-a+b+c.故选D.
解法二:由题意得a+b+c.故选D.
方法总结 对于爪形图线段中的分点问题,常用的结论如下:如图,在△ABC中,D是线段BC上一点(不含端点),且,则.
8.C 对于A,若A,B,C三点共线,则存在唯一的实数λ,使得,即e1+2e2=λ(-3e1+2e2),则无解,所以A,B,C三点不共线,故A错误;
对于B,若A,B,D三点共线,则存在唯一的实数μ,使得,即e1+2e2=μ(3e1-6e2),则无解,所以A,B,D三点不共线,故B错误;
对于C,易得=(e1+2e2)+(-3e1+2e2)=-2e1+4e2=,且AC,AD有公共点A,所以A,C,D三点共线,故C正确;
对于D,易得=(3e1-6e2)+(e1+2e2)=4e1-4e2,若B,C,D三点共线,则存在唯一的实数k,使得,即4e1-4e2=k(-3e1+2e2),则无解,所以B,C,D三点不共线,故D错误.故选C.
9.B 对于A,当λ=0时,,所以,又μ∈[0,1],所以点P在棱BB1上,故A中说法正确;
对于B,当λ=μ时,),即,故,又λ∈[0,1],所以点P在线段BC1上,故B中说法错误;
对于C,当μ=1时,,所以λ,即,故,又λ∈[0,1],所以点P在棱B1C1上,故C中说法正确;
对于D,当λ+μ=1时,,即,即,故,又λ∈[0,1],所以点P在线段B1C上,故D中说法正确.
故选B.
能力提升练
1.D 2.B 3.B
1.D 因为F为BE的中点,所以,
又,所以.
由,得),即,所以λ=.故选D.
2.B 因为E,F分别为BC,AE的中点,所以).
因为G为△ACD的重心,所以),
所以.故选B.
知识总结 若G为△ABC的重心,则).
3.B 在△PAE中,,
∵PE=EC,
∴PE=PC,即,
又=a+b-c,
∴=c+(a+b-c)=a+b+c.
故选B.
4.答案 0
解析 因为A,B,C三点共线,所以存在唯一的实数k使,显然k≠0且k≠1,否则点A,B重合或点B,C重合,故),整理得(k-1)=0,又λ=0,所以λ=k-1,m=1,n=-k,显然实数λ,m,n均不为0,所以λ+m+n的值为0.
5.证明 连接BD.∵E,H分别是AB,AD的中点,且,
∴,
∴,且||≠||.
又F不在EH上,∴四边形EFGH是梯形.
6.解析 (1)∵A'M=,
∴a-b-c.
∵A'N=),
∴a-b-c.
(2)证明:∵,且,
∴,即M,N,D'三点共线.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
