2025苏教版高中数学选择性必修第二册强化练习题(含解析)--6.2.2 空间向量的坐标表示
文档属性
| 名称 | 2025苏教版高中数学选择性必修第二册强化练习题(含解析)--6.2.2 空间向量的坐标表示 |

|
|
| 格式 | docx | ||
| 文件大小 | 466.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-15 16:29:07 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025苏教版高中数学选择性必修第二册
6.2.2 空间向量的坐标表示
基础过关练
题组一 空间向量的坐标表示与运算
1.(2024湖北武汉外国语学校期末)已知a=(1,2,3),a+b=(-1,3,5),则b=( )
A.(2,-2,2) B.(-2,1,2)
C.(-2,-1,2) D.(2,-1,2)
2.(2024江苏南通崇川、通州联考)在空间直角坐标系中,点A(9,8,5)关于xOz平面对称的点的坐标为( )
A.(9,8,-5) B.(9,-8,5)
C.(-9,8,5) D.(-9,8,-5)
3.(2023江苏连云港海州高级中学调研)已知空间直角坐标系中,A(4,1,3),B(2,-5,1),点C满足,则点C的坐标为( )
A.(3,-2,2) B.(-2,-6,-2)
C.(6,-4,4) D.(0,-11,-1)
4.(2024江苏连云港期中)已知{a,b,c}是空间的一个基底,{a+b,a-b,c}是空间的另一个基底,向量p在基底{a,b,c}下的坐标为(4,2,3),则向量p在基底{a+b,a-b,c}下的坐标是( )
A.(4,0,3) B.(3,1,3)
C.(1,2,3) D.(2,1,3)
5.(多选题)(2024江苏盐城期末)在空间直角坐标系中,已知某平行四边形的三个顶点的坐标分别为(1,2,3),(3,4,2),(-1,4,6),则第四个顶点的坐标可能为( )
A.(5,2,-1) B.(-3,2,7)
C.(5,2,7) D.(1,6,5)
6.已知O是坐标原点,且A,B,C三点的坐标分别是(2,-1,2),(4,5,-1),(-2,2,3),若),则点P的坐标为 ;若),则点P的坐标为 .
题组二 空间向量平行(共线)的坐标表示
7.(2023江苏淮安高中校协作体期中)如果三点A(1,5,-2),B(2,4,1),C(a,3,b+2)在同一条直线上,则( )
A.a=3,b=2 B.a=6,b=-1
C.a=3,b=-3 D.a=-2,b=1
8.(2024江苏盐城三校联考)已知向量a=(-1,1,0),b=(1,0,m),且ka+b与a-2b平行,则k= .
题组三 空间向量数量积的坐标表示及应用
9.(2023江苏连云港海头高级中学期中)已知a=(1,n,2),b=(-2,1,2),若2a-b与b垂直,则|a|=( )
A.
10.(多选题)(2024江苏睢宁高级中学学情检测)已知a=(-2,-1,1),b=(3,4,5),则下列结论正确的是( )
A.(2a+b)∥a
B.5|a|=|b|
C.a⊥(5a+6b)
D.a与b夹角的余弦值为-
11.(2024山东枣庄辅仁高级中学月考)若a=(2,3,-1),b=(-1,0,3),c=(0,1,2),则a·(2b-3c)= ;(a+b)·(c+b)= .
12.(2024北京通州期中)在空间直角坐标系O-xyz中,已知=(0,0,2),则的夹角的余弦值为 ;上的投影向量为 .
13.(2024江苏扬州丁沟中学月考)已知向量a=(x,1,2),b=(1,y,-2),c=(3,1,z),且a∥b,b⊥c.
(1)求向量a,b,c的坐标;
(2)求a+c与b+c所成角的余弦值.
题组四 空间直角坐标系的应用
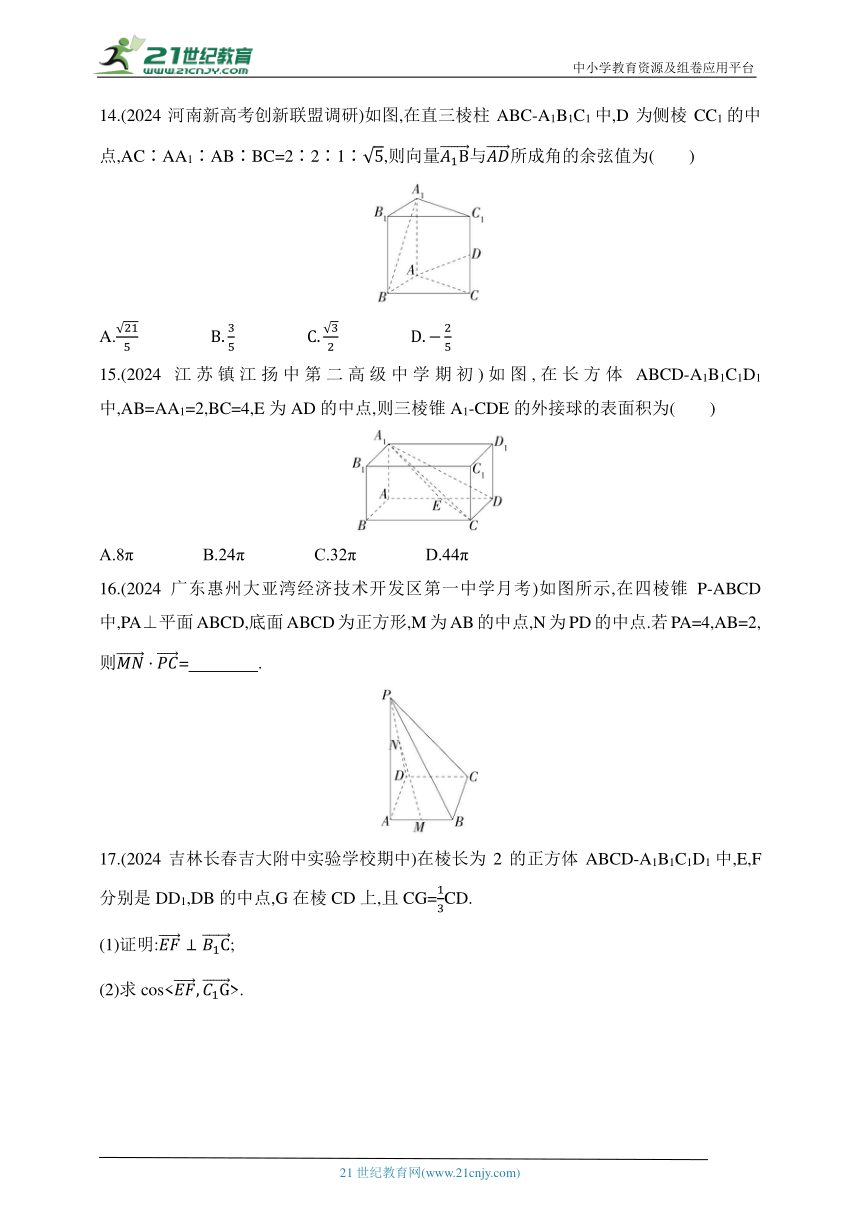
14.(2024河南新高考创新联盟调研)如图,在直三棱柱ABC-A1B1C1中,D为侧棱CC1的中点,AC∶AA1∶AB∶BC=2∶2∶1∶,则向量所成角的余弦值为( )
A.
15.(2024江苏镇江扬中第二高级中学期初)如图,在长方体ABCD-A1B1C1D1中,AB=AA1=2,BC=4,E为AD的中点,则三棱锥A1-CDE的外接球的表面积为( )
A.8π B.24π C.32π D.44π
16.(2024广东惠州大亚湾经济技术开发区第一中学月考)如图所示,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为正方形,M为AB的中点,N为PD的中点.若PA=4,AB=2,则= .
17.(2024吉林长春吉大附中实验学校期中)在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是DD1,DB的中点,G在棱CD上,且CG=CD.
(1)证明:;
(2)求cos<>.
能力提升练
题组一 空间向量的坐标运算
1.(2024江苏南京第九中学期末)在空间直角坐标系中,已知a=(1,-2,-1),b=(-1,x-1,1),且a与b的夹角为钝角,则x的取值范围是( )
A.(0,+∞) B.(0,3)
C.(3,+∞) D.(0,3)∪(3,+∞)
2.(2024山东泰安一中诊断)在空间直角坐标系O-xyz中,=(1,1,2),点Q在直线OP上运动,则当取得最小值时,点Q的坐标为( )
A. B.
C. D.
3.在空间直角坐标系O-xyz中,O(0,0,0),E(2,0),B为EF的中点,C为空间中一点,且满足||=3,若cos<,则=( )
A.9 B.7 C.5 D.3
4.(2024江苏扬州江都中学联考)已知空间三点A(0,2,3),B(-2,1,6),C(1,-1,5).
(1)求以AB和AC为邻边的平行四边形的面积;
(2)试判断点P(-3,-3,11)与点A,B,C是否共面,并说明理由.
题组二 空间直角坐标系的应用
5.(2024江苏常熟抽测)如图,圆台OO1的轴截面为等腰梯形ABCD,AB=2CD,E在上底面的圆周上,且∠CO1E=45°,则上的投影向量为( )
A. B.
C. D.
6.(2023江苏南通如东、海安期中)已知正六棱柱ABCDEF-A1B1C1D1E1F1的底面边长为1,P是正六棱柱内(不含表面)的一点,则的取值范围是 .
7.(2024江苏南京金陵中学检测)在正三棱柱ABC-A1B1C1中,AB=2,AA1=,O为BC的中点,M为棱B1C1上的动点,N为棱AM上的动点,且,则线段MN的长度的取值范围为 .
8.(2024福建泉州实验中学月考)在正四棱柱ABCD-A1B1C1D1中,底面ABCD是边长为4的正方形,A1C1与B1D1交于点N,BC1与B1C交于点M,连接AM,BN,且.
(1)用向量法求AA1的长;
(2)对于n个向量a1,a2,…,an,如果存在不全为零的n个实数λ1,λ2,…,λn,使得λ1a1+λ2a2+…+λnan=0,则称n个向量a1,a2,…,an线性相关,否则称为线性无关.试判断是否线性相关.
答案与分层梯度式解析
6.2.2 空间向量的坐标表示
基础过关练
1.B 2.B 3.A 4.B 5.ABD 7.A 9.B 10.BCD
14.D 15.D
1.B 由题意,得b=(a+b)-a=(-1,3,5)-(1,2,3)=(-2,1,2).故选B.
2.B 点A(9,8,5)关于xOz平面对称的点的坐标为(9,-8,5).故选B.
方法技巧 空间中点的对称规律:关于谁对称谁不变,其余坐标均相反.
3.A 由,可得C为AB的中点,因为A(4,1,3),B(2,-5,1),所以C(3,-2,2),故选A.
4.B 设向量p在基底{a+b,a-b,c}下的坐标为(x,y,z),则p=x(a+b)+y(a-b)+zc,
因为向量p在基底{a,b,c}下的坐标为(4,2,3),所以p=4a+2b+3c,
所以4a+2b+3c=x(a+b)+y(a-b)+zc,即4a+2b+3c=(x+y)a+(x-y)b+zc,
所以所以向量p在基底{a+b,a-b,c}下的坐标为(3,1,3).故选B.
5.ABD 记点A的坐标为(1,2,3),点B的坐标为(3,4,2),点C的坐标为(-1,4,6),设该平行四边形的第四个顶点为D(x,y,z),
易知对角线互相平分的四边形是平行四边形,所以可分三种情况:
①若AD与BC的中点重合,
则
②若BD与AC的中点重合,
则
③若CD与AB的中点重合,
则
所以第四个顶点的坐标可能为(1,6,5)或(-3,2,7)或(5,2,-1).故选ABD.
6.答案
解析 由题得=(-4,3,1).
若,则P.
若,
则.
7.A ∵A,B,C三点共线,
∴为共线向量,又=(a-1,-2,b+4),
∴,解得a=3,b=2.
8.答案 -
解析 根据题意,得ka+b=(1-k,k,m),a-2b=(-3,1,-2m).
因为ka+b与a-2b平行,
所以当m=0时,,解得k=-;
当m≠0时,,解得k=-.
综上,k=-.
9.B 由题意得2a-b=(4,2n-1,2),
因为2a-b与b垂直,
所以(2a-b)·b=(4,2n-1,2)·(-2,1,2)=4×(-2)+(2n-1)×1+2×2=0,解得n=,
所以a=,所以|a|=.故选B.
10.BCD 因为2a+b=2(-2,-1,1)+(3,4,5)=(-1,2,7),a=(-2,-1,1),且,所以2a+b与a不平行,故A中结论错误;
由题知,|a|=,|b|=,所以5|a|=|b|,故B中结论正确;
易得5a+6b=(8,19,35),则a·(5a+6b)=(-2)×8-1×19+1×35=0,所以a⊥(5a+6b),故C中结论正确;
由a=(-2,-1,1),b=(3,4,5),得cos=,故D中结论正确.
故选BCD.
11.答案 -13;12
解析 因为b=(-1,0,3),c=(0,1,2),所以2b=(-2,0,6),3c=(0,3,6),所以2b-3c=(-2,-3,0),
故a·(2b-3c)=(2,3,-1)·(-2,-3,0)=-4-9+0=-13.
由a=(2,3,-1),b=(-1,0,3),c=(0,1,2),可得a+b=(1,3,2),b+c=(-1,1,5),
故(a+b)·(c+b)=-1+3+10=12.
12.答案 ;(1,-1,0)
解析 因为=(0,0,2),所以=(2,-2,0),
所以cos<,
则上的投影向量为|>·=(1,-1,0).
13.解析 (1)易知y≠0,∵a=(x,1,2),b=(1,y,-2),c=(3,1,z),且a∥b,b⊥c,
∴
∴a=(-1,1,2),b=(1,-1,-2),c=(3,1,1).
(2)由(1)知,a+c=(2,2,3),b+c=(4,0,-1),
∴(a+c)·(b+c)=2×4+2×0+3×(-1)=5,
|a+c|=,
|b+c|=,
设a+c与b+c所成的角为θ,
则cos θ=,
故a+c与b+c所成角的余弦值为.
14.D 不妨设AC=AA1=2,AB=1,BC=,则AB2+AC2=BC2,所以∠BAC=90°,即AB⊥AC,
在直三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AC,AB 平面ABC,所以AA1⊥AC,AA1⊥AB.
以A为坐标原点建立空间直角坐标系A-xyz,如图所示,
则A(0,0,0),A1(0,0,2),B(1,0,0),D(0,2,1),
所以=(0,2,1),
所以cos<,
故所成角的余弦值为-.故选D.
15.D 以A为原点建立如图所示的空间直角坐标系A-xyz,
则A1(0,0,2),C(2,4,0),D(0,4,0),E(0,2,0),
设三棱锥A1-CDE的外接球的球心为O(x,y,z),
则OA1=OC=OD=OE,
由OD=OE,得,解得y=3,
由OC=OD,得,解得x=1,
由OA1=OC,得,即,解得z=3,
所以O(1,3,3),因此三棱锥A1-CDE的外接球的半径为,
故该外接球的表面积为4π·()2=44π.故选D.
16.答案 -8
解析 以A为坐标原点,的方向分别为x轴,y轴,z轴的正方向建立空间直角坐标系,如图,
则A(0,0,0),B(2,0,0),D(0,2,0),P(0,0,4),C(2,2,0),所以=(2,2,-4),
因为M为AB的中点,N为PD的中点,
所以M(1,0,0),N(0,1,2),
所以=(-1,1,2),所以=-2+2-8=-8.
17.解析 (1)证明:以D为原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系,
则D(0,0,0),E(0,0,1),F(1,1,0),C(0,2,0),C1(0,2,2),B1(2,2,2),G,
所以=(-2,0,-2),
所以=1×(-2)+1×0+(-1)×(-2)=0,
所以.
(2)由(1)知,=(1,1,-1),
所以|,
所以cos<.
能力提升练
1.D 2.C 3.D 5.B
1.D 因为a与b的夹角为钝角,所以a·b<0,且a与b不共线,
又a=(1,-2,-1),b=(-1,x-1,1),所以a·b=1×(-1)-2×(x-1)-1×1=-2x<0,解得x>0,
若a与b共线,则,即x=3,
所以x的取值范围为x>0且x≠3,即x∈(0,3)∪(3,+∞).故选D.
2.C 设Q(x,y,z),由点Q在直线OP上,可得存在实数λ,使得,即(x,y,z)=λ(1,1,2),所以Q(λ,λ,2λ),所以=(2-λ,1-λ,2-2λ),则=(1-λ)(2-λ)+(2-λ)·(1-λ)+(3-2λ)(2-2λ)=2(3λ2-8λ+5),根据二次函数的性质,可得当λ=时,取得最小值,为-,此时Q.故选C.
3.D 易得B(,0),设C(x,y,z),则,z),
由cos<
=,
得x-y=-①.
由||=3,得,化简,得x+y=②.
联立①②,解得x=,所以,易得,0),所以·(0,2,0)=3.故选D.
4.解析 (1)由已知可得,=(1,-3,2),
∴cos A=cos<,又0故以AB,AC为邻边的平行四边形的面积为||·||·sin A=.
(2)点P与点A,B,C共面,理由如下:
由题得=(1,-3,2),
假设存在实数λ,μ,使得,
则
∴,即是共面向量,
∴点P与点A,B,C共面.
5.B 连接OO1,则OO1⊥底面圆O,以点O为坐标原点建立空间直角坐标系O-xyz,如图所示,
不妨设圆台OO1的高为h,CD=4a,则AB=8a,
故A(0,-4a,0),B(0,4a,0),E(-a,h),
则)a,h),
所以)a2,
所以.故选B.
6.答案
解析 以A为坐标原点,建立如图所示的空间直角坐标系A-xyz,且AB=BC=CD=DE=EF=AF=1,
由正六边形的性质可得,A(0,0,0),B(1,0,0),F,所以=(1,0,0),
设P(x,y,z),其中-,
则=(x,y,z),
所以=x,故.
7.答案
解析 取B1C1的中点Q,连接OQ,OA,易得OQ,OA,OC互相垂直.
以O为坐标原点,OC,OA,OQ所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,如图,
则O(0,0,0),A(0,),
因为M是棱B1C1上一动点,所以设M(a,0,),且a∈[-1,1],
因为,所以MN=,
令t=,a∈[-1,1],则,t∈[],
又函数y=t-在t∈[]上单调递增,
所以当t=时,,当t=时,,
所以线段MN的长度的取值范围为.
8.解析 (1)以D为坐标原点,的方向分别为x轴,y轴,z轴的正方向,建立如图所示的空间直角坐标系,
则A(4,0,0),B(4,4,0),
设AA1=t(t>0),则M,N(2,2,t),
所以=(-2,-2,t),
由,得=0,即-2×(-2)+4×(-2)+t2=0,解得t=2(负值舍去),
故AA1=2.
(2)由(1)知=(0,-4,0),
设存在实数λ1,λ2,λ3,使得λ1=0成立,
则
即当且仅当λ1=λ2=λ3=0时,λ1=0,
∴线性无关.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025苏教版高中数学选择性必修第二册
6.2.2 空间向量的坐标表示
基础过关练
题组一 空间向量的坐标表示与运算
1.(2024湖北武汉外国语学校期末)已知a=(1,2,3),a+b=(-1,3,5),则b=( )
A.(2,-2,2) B.(-2,1,2)
C.(-2,-1,2) D.(2,-1,2)
2.(2024江苏南通崇川、通州联考)在空间直角坐标系中,点A(9,8,5)关于xOz平面对称的点的坐标为( )
A.(9,8,-5) B.(9,-8,5)
C.(-9,8,5) D.(-9,8,-5)
3.(2023江苏连云港海州高级中学调研)已知空间直角坐标系中,A(4,1,3),B(2,-5,1),点C满足,则点C的坐标为( )
A.(3,-2,2) B.(-2,-6,-2)
C.(6,-4,4) D.(0,-11,-1)
4.(2024江苏连云港期中)已知{a,b,c}是空间的一个基底,{a+b,a-b,c}是空间的另一个基底,向量p在基底{a,b,c}下的坐标为(4,2,3),则向量p在基底{a+b,a-b,c}下的坐标是( )
A.(4,0,3) B.(3,1,3)
C.(1,2,3) D.(2,1,3)
5.(多选题)(2024江苏盐城期末)在空间直角坐标系中,已知某平行四边形的三个顶点的坐标分别为(1,2,3),(3,4,2),(-1,4,6),则第四个顶点的坐标可能为( )
A.(5,2,-1) B.(-3,2,7)
C.(5,2,7) D.(1,6,5)
6.已知O是坐标原点,且A,B,C三点的坐标分别是(2,-1,2),(4,5,-1),(-2,2,3),若),则点P的坐标为 ;若),则点P的坐标为 .
题组二 空间向量平行(共线)的坐标表示
7.(2023江苏淮安高中校协作体期中)如果三点A(1,5,-2),B(2,4,1),C(a,3,b+2)在同一条直线上,则( )
A.a=3,b=2 B.a=6,b=-1
C.a=3,b=-3 D.a=-2,b=1
8.(2024江苏盐城三校联考)已知向量a=(-1,1,0),b=(1,0,m),且ka+b与a-2b平行,则k= .
题组三 空间向量数量积的坐标表示及应用
9.(2023江苏连云港海头高级中学期中)已知a=(1,n,2),b=(-2,1,2),若2a-b与b垂直,则|a|=( )
A.
10.(多选题)(2024江苏睢宁高级中学学情检测)已知a=(-2,-1,1),b=(3,4,5),则下列结论正确的是( )
A.(2a+b)∥a
B.5|a|=|b|
C.a⊥(5a+6b)
D.a与b夹角的余弦值为-
11.(2024山东枣庄辅仁高级中学月考)若a=(2,3,-1),b=(-1,0,3),c=(0,1,2),则a·(2b-3c)= ;(a+b)·(c+b)= .
12.(2024北京通州期中)在空间直角坐标系O-xyz中,已知=(0,0,2),则的夹角的余弦值为 ;上的投影向量为 .
13.(2024江苏扬州丁沟中学月考)已知向量a=(x,1,2),b=(1,y,-2),c=(3,1,z),且a∥b,b⊥c.
(1)求向量a,b,c的坐标;
(2)求a+c与b+c所成角的余弦值.
题组四 空间直角坐标系的应用
14.(2024河南新高考创新联盟调研)如图,在直三棱柱ABC-A1B1C1中,D为侧棱CC1的中点,AC∶AA1∶AB∶BC=2∶2∶1∶,则向量所成角的余弦值为( )
A.
15.(2024江苏镇江扬中第二高级中学期初)如图,在长方体ABCD-A1B1C1D1中,AB=AA1=2,BC=4,E为AD的中点,则三棱锥A1-CDE的外接球的表面积为( )
A.8π B.24π C.32π D.44π
16.(2024广东惠州大亚湾经济技术开发区第一中学月考)如图所示,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为正方形,M为AB的中点,N为PD的中点.若PA=4,AB=2,则= .
17.(2024吉林长春吉大附中实验学校期中)在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是DD1,DB的中点,G在棱CD上,且CG=CD.
(1)证明:;
(2)求cos<>.
能力提升练
题组一 空间向量的坐标运算
1.(2024江苏南京第九中学期末)在空间直角坐标系中,已知a=(1,-2,-1),b=(-1,x-1,1),且a与b的夹角为钝角,则x的取值范围是( )
A.(0,+∞) B.(0,3)
C.(3,+∞) D.(0,3)∪(3,+∞)
2.(2024山东泰安一中诊断)在空间直角坐标系O-xyz中,=(1,1,2),点Q在直线OP上运动,则当取得最小值时,点Q的坐标为( )
A. B.
C. D.
3.在空间直角坐标系O-xyz中,O(0,0,0),E(2,0),B为EF的中点,C为空间中一点,且满足||=3,若cos<,则=( )
A.9 B.7 C.5 D.3
4.(2024江苏扬州江都中学联考)已知空间三点A(0,2,3),B(-2,1,6),C(1,-1,5).
(1)求以AB和AC为邻边的平行四边形的面积;
(2)试判断点P(-3,-3,11)与点A,B,C是否共面,并说明理由.
题组二 空间直角坐标系的应用
5.(2024江苏常熟抽测)如图,圆台OO1的轴截面为等腰梯形ABCD,AB=2CD,E在上底面的圆周上,且∠CO1E=45°,则上的投影向量为( )
A. B.
C. D.
6.(2023江苏南通如东、海安期中)已知正六棱柱ABCDEF-A1B1C1D1E1F1的底面边长为1,P是正六棱柱内(不含表面)的一点,则的取值范围是 .
7.(2024江苏南京金陵中学检测)在正三棱柱ABC-A1B1C1中,AB=2,AA1=,O为BC的中点,M为棱B1C1上的动点,N为棱AM上的动点,且,则线段MN的长度的取值范围为 .
8.(2024福建泉州实验中学月考)在正四棱柱ABCD-A1B1C1D1中,底面ABCD是边长为4的正方形,A1C1与B1D1交于点N,BC1与B1C交于点M,连接AM,BN,且.
(1)用向量法求AA1的长;
(2)对于n个向量a1,a2,…,an,如果存在不全为零的n个实数λ1,λ2,…,λn,使得λ1a1+λ2a2+…+λnan=0,则称n个向量a1,a2,…,an线性相关,否则称为线性无关.试判断是否线性相关.
答案与分层梯度式解析
6.2.2 空间向量的坐标表示
基础过关练
1.B 2.B 3.A 4.B 5.ABD 7.A 9.B 10.BCD
14.D 15.D
1.B 由题意,得b=(a+b)-a=(-1,3,5)-(1,2,3)=(-2,1,2).故选B.
2.B 点A(9,8,5)关于xOz平面对称的点的坐标为(9,-8,5).故选B.
方法技巧 空间中点的对称规律:关于谁对称谁不变,其余坐标均相反.
3.A 由,可得C为AB的中点,因为A(4,1,3),B(2,-5,1),所以C(3,-2,2),故选A.
4.B 设向量p在基底{a+b,a-b,c}下的坐标为(x,y,z),则p=x(a+b)+y(a-b)+zc,
因为向量p在基底{a,b,c}下的坐标为(4,2,3),所以p=4a+2b+3c,
所以4a+2b+3c=x(a+b)+y(a-b)+zc,即4a+2b+3c=(x+y)a+(x-y)b+zc,
所以所以向量p在基底{a+b,a-b,c}下的坐标为(3,1,3).故选B.
5.ABD 记点A的坐标为(1,2,3),点B的坐标为(3,4,2),点C的坐标为(-1,4,6),设该平行四边形的第四个顶点为D(x,y,z),
易知对角线互相平分的四边形是平行四边形,所以可分三种情况:
①若AD与BC的中点重合,
则
②若BD与AC的中点重合,
则
③若CD与AB的中点重合,
则
所以第四个顶点的坐标可能为(1,6,5)或(-3,2,7)或(5,2,-1).故选ABD.
6.答案
解析 由题得=(-4,3,1).
若,则P.
若,
则.
7.A ∵A,B,C三点共线,
∴为共线向量,又=(a-1,-2,b+4),
∴,解得a=3,b=2.
8.答案 -
解析 根据题意,得ka+b=(1-k,k,m),a-2b=(-3,1,-2m).
因为ka+b与a-2b平行,
所以当m=0时,,解得k=-;
当m≠0时,,解得k=-.
综上,k=-.
9.B 由题意得2a-b=(4,2n-1,2),
因为2a-b与b垂直,
所以(2a-b)·b=(4,2n-1,2)·(-2,1,2)=4×(-2)+(2n-1)×1+2×2=0,解得n=,
所以a=,所以|a|=.故选B.
10.BCD 因为2a+b=2(-2,-1,1)+(3,4,5)=(-1,2,7),a=(-2,-1,1),且,所以2a+b与a不平行,故A中结论错误;
由题知,|a|=,|b|=,所以5|a|=|b|,故B中结论正确;
易得5a+6b=(8,19,35),则a·(5a+6b)=(-2)×8-1×19+1×35=0,所以a⊥(5a+6b),故C中结论正确;
由a=(-2,-1,1),b=(3,4,5),得cos
故选BCD.
11.答案 -13;12
解析 因为b=(-1,0,3),c=(0,1,2),所以2b=(-2,0,6),3c=(0,3,6),所以2b-3c=(-2,-3,0),
故a·(2b-3c)=(2,3,-1)·(-2,-3,0)=-4-9+0=-13.
由a=(2,3,-1),b=(-1,0,3),c=(0,1,2),可得a+b=(1,3,2),b+c=(-1,1,5),
故(a+b)·(c+b)=-1+3+10=12.
12.答案 ;(1,-1,0)
解析 因为=(0,0,2),所以=(2,-2,0),
所以cos<,
则上的投影向量为|>·=(1,-1,0).
13.解析 (1)易知y≠0,∵a=(x,1,2),b=(1,y,-2),c=(3,1,z),且a∥b,b⊥c,
∴
∴a=(-1,1,2),b=(1,-1,-2),c=(3,1,1).
(2)由(1)知,a+c=(2,2,3),b+c=(4,0,-1),
∴(a+c)·(b+c)=2×4+2×0+3×(-1)=5,
|a+c|=,
|b+c|=,
设a+c与b+c所成的角为θ,
则cos θ=,
故a+c与b+c所成角的余弦值为.
14.D 不妨设AC=AA1=2,AB=1,BC=,则AB2+AC2=BC2,所以∠BAC=90°,即AB⊥AC,
在直三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AC,AB 平面ABC,所以AA1⊥AC,AA1⊥AB.
以A为坐标原点建立空间直角坐标系A-xyz,如图所示,
则A(0,0,0),A1(0,0,2),B(1,0,0),D(0,2,1),
所以=(0,2,1),
所以cos<,
故所成角的余弦值为-.故选D.
15.D 以A为原点建立如图所示的空间直角坐标系A-xyz,
则A1(0,0,2),C(2,4,0),D(0,4,0),E(0,2,0),
设三棱锥A1-CDE的外接球的球心为O(x,y,z),
则OA1=OC=OD=OE,
由OD=OE,得,解得y=3,
由OC=OD,得,解得x=1,
由OA1=OC,得,即,解得z=3,
所以O(1,3,3),因此三棱锥A1-CDE的外接球的半径为,
故该外接球的表面积为4π·()2=44π.故选D.
16.答案 -8
解析 以A为坐标原点,的方向分别为x轴,y轴,z轴的正方向建立空间直角坐标系,如图,
则A(0,0,0),B(2,0,0),D(0,2,0),P(0,0,4),C(2,2,0),所以=(2,2,-4),
因为M为AB的中点,N为PD的中点,
所以M(1,0,0),N(0,1,2),
所以=(-1,1,2),所以=-2+2-8=-8.
17.解析 (1)证明:以D为原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系,
则D(0,0,0),E(0,0,1),F(1,1,0),C(0,2,0),C1(0,2,2),B1(2,2,2),G,
所以=(-2,0,-2),
所以=1×(-2)+1×0+(-1)×(-2)=0,
所以.
(2)由(1)知,=(1,1,-1),
所以|,
所以cos<.
能力提升练
1.D 2.C 3.D 5.B
1.D 因为a与b的夹角为钝角,所以a·b<0,且a与b不共线,
又a=(1,-2,-1),b=(-1,x-1,1),所以a·b=1×(-1)-2×(x-1)-1×1=-2x<0,解得x>0,
若a与b共线,则,即x=3,
所以x的取值范围为x>0且x≠3,即x∈(0,3)∪(3,+∞).故选D.
2.C 设Q(x,y,z),由点Q在直线OP上,可得存在实数λ,使得,即(x,y,z)=λ(1,1,2),所以Q(λ,λ,2λ),所以=(2-λ,1-λ,2-2λ),则=(1-λ)(2-λ)+(2-λ)·(1-λ)+(3-2λ)(2-2λ)=2(3λ2-8λ+5),根据二次函数的性质,可得当λ=时,取得最小值,为-,此时Q.故选C.
3.D 易得B(,0),设C(x,y,z),则,z),
由cos<
=,
得x-y=-①.
由||=3,得,化简,得x+y=②.
联立①②,解得x=,所以,易得,0),所以·(0,2,0)=3.故选D.
4.解析 (1)由已知可得,=(1,-3,2),
∴cos A=cos<,又0
(2)点P与点A,B,C共面,理由如下:
由题得=(1,-3,2),
假设存在实数λ,μ,使得,
则
∴,即是共面向量,
∴点P与点A,B,C共面.
5.B 连接OO1,则OO1⊥底面圆O,以点O为坐标原点建立空间直角坐标系O-xyz,如图所示,
不妨设圆台OO1的高为h,CD=4a,则AB=8a,
故A(0,-4a,0),B(0,4a,0),E(-a,h),
则)a,h),
所以)a2,
所以.故选B.
6.答案
解析 以A为坐标原点,建立如图所示的空间直角坐标系A-xyz,且AB=BC=CD=DE=EF=AF=1,
由正六边形的性质可得,A(0,0,0),B(1,0,0),F,所以=(1,0,0),
设P(x,y,z),其中-,
则=(x,y,z),
所以=x,故.
7.答案
解析 取B1C1的中点Q,连接OQ,OA,易得OQ,OA,OC互相垂直.
以O为坐标原点,OC,OA,OQ所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,如图,
则O(0,0,0),A(0,),
因为M是棱B1C1上一动点,所以设M(a,0,),且a∈[-1,1],
因为,所以MN=,
令t=,a∈[-1,1],则,t∈[],
又函数y=t-在t∈[]上单调递增,
所以当t=时,,当t=时,,
所以线段MN的长度的取值范围为.
8.解析 (1)以D为坐标原点,的方向分别为x轴,y轴,z轴的正方向,建立如图所示的空间直角坐标系,
则A(4,0,0),B(4,4,0),
设AA1=t(t>0),则M,N(2,2,t),
所以=(-2,-2,t),
由,得=0,即-2×(-2)+4×(-2)+t2=0,解得t=2(负值舍去),
故AA1=2.
(2)由(1)知=(0,-4,0),
设存在实数λ1,λ2,λ3,使得λ1=0成立,
则
即当且仅当λ1=λ2=λ3=0时,λ1=0,
∴线性无关.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
