2025苏教版高中数学选择性必修第二册强化练习题(含解析)--6.3.4 空间距离的计算
文档属性
| 名称 | 2025苏教版高中数学选择性必修第二册强化练习题(含解析)--6.3.4 空间距离的计算 |

|
|
| 格式 | docx | ||
| 文件大小 | 599.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-15 16:29:34 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025苏教版高中数学选择性必修第二册
6.3.4 空间距离的计算
基础过关练
题组一 点到直线的距离的计算
1.(2024江苏南通质量监测)在空间直角坐标系中,已知点A(1,1,1),B(0,1,0),C(1,2,3),则点C到直线AB的距离为( )
A. D.3
2.(2024安徽六安新安中学期中)如图,几何体ABCD-EFGH是棱长为6的正方体,若,则点P到直线CH的距离为( )
A.4 B.3 C.2 D.1
3.(2024江苏南京金陵中学检测)四面体OABC满足∠AOB=∠BOC=∠COA=90°,OA=1,OB=2,OC=3,点D在棱OC上,且OC=3OD,点G为△ABC的重心,则点G到直线AD的距离为( )
A.
题组二 点到平面的距离的计算
4.(2024江苏无锡太湖高级中学月考)已知平面α的一个法向量为n=(1,2,1),A(1,0,-1),B(0,-1,1),且A α,B∈α,则点A到平面α的距离为( )
A. D.1
5.(2023江苏常州武进检测)已知正方体ABCD-A1B1C1D1的棱长为2,E,F分别为上底面A1B1C1D1和侧面CDD1C1的中心,则点C到平面AEF的距离为( )
A.
题组三 直线与直线、直线与平面、平面与平面间的距离的计算
6.(2023湖北荆门月考)在棱长为1的正方体ABCD-A1B1C1D1中,M,N分别为棱A1B1,BB1的中点,则异面直线AM与CN间的距离为 .
7.(2024江苏无锡辅仁高级中学期中)在棱长为3的正方体ABCD-A1B1C1D1中,E为线段DD1靠近D1的三等分点,F为线段BB1靠近B的三等分点,则直线FC1到平面AB1E的距离为 .
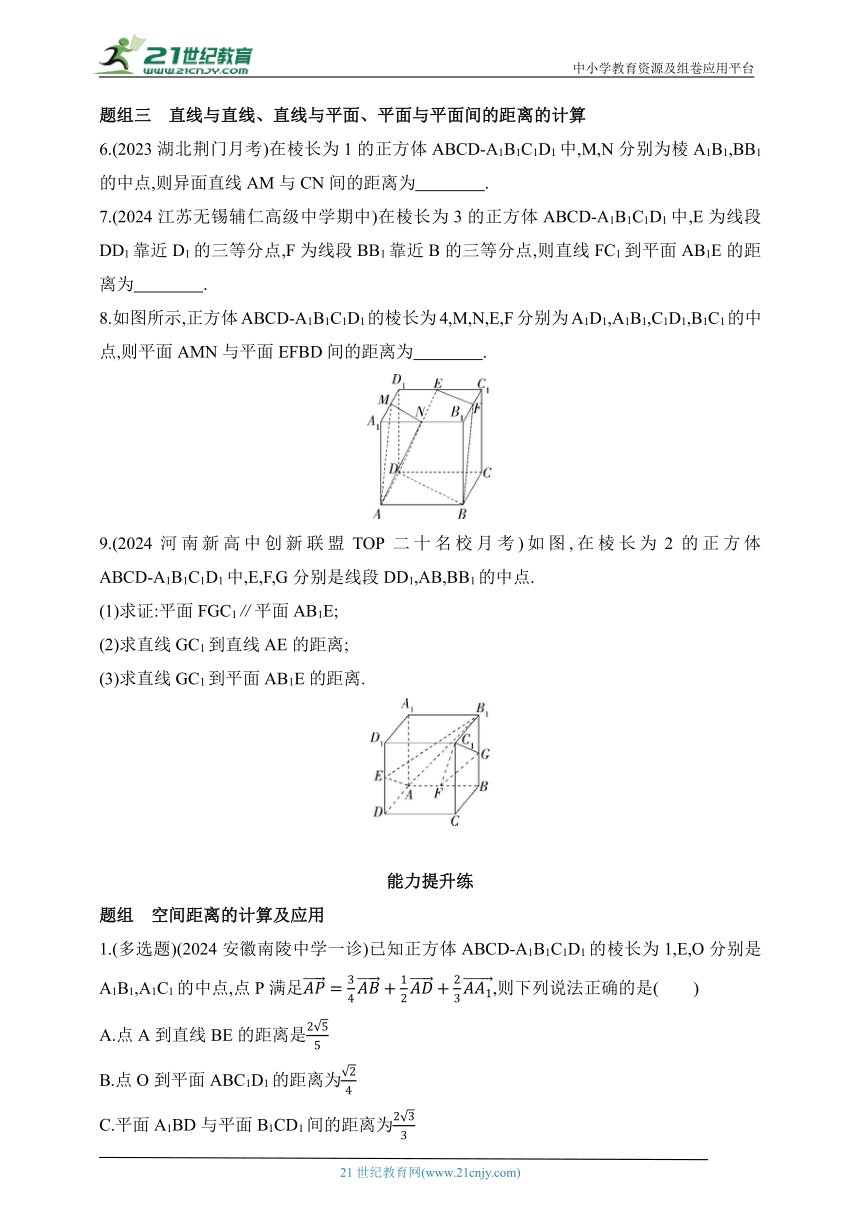
8.如图所示,正方体ABCD-A1B1C1D1的棱长为4,M,N,E,F分别为A1D1,A1B1,C1D1,B1C1的中点,则平面AMN与平面EFBD间的距离为 .
9.(2024河南新高中创新联盟TOP二十名校月考)如图,在棱长为2的正方体ABCD-A1B1C1D1中,E,F,G分别是线段DD1,AB,BB1的中点.
(1)求证:平面FGC1∥平面AB1E;
(2)求直线GC1到直线AE的距离;
(3)求直线GC1到平面AB1E的距离.
能力提升练
题组 空间距离的计算及应用
1.(多选题)(2024安徽南陵中学一诊)已知正方体ABCD-A1B1C1D1的棱长为1,E,O分别是A1B1,A1C1的中点,点P满足,则下列说法正确的是( )
A.点A到直线BE的距离是
B.点O到平面ABC1D1的距离为
C.平面A1BD与平面B1CD1间的距离为
D.点P到直线AB的距离为
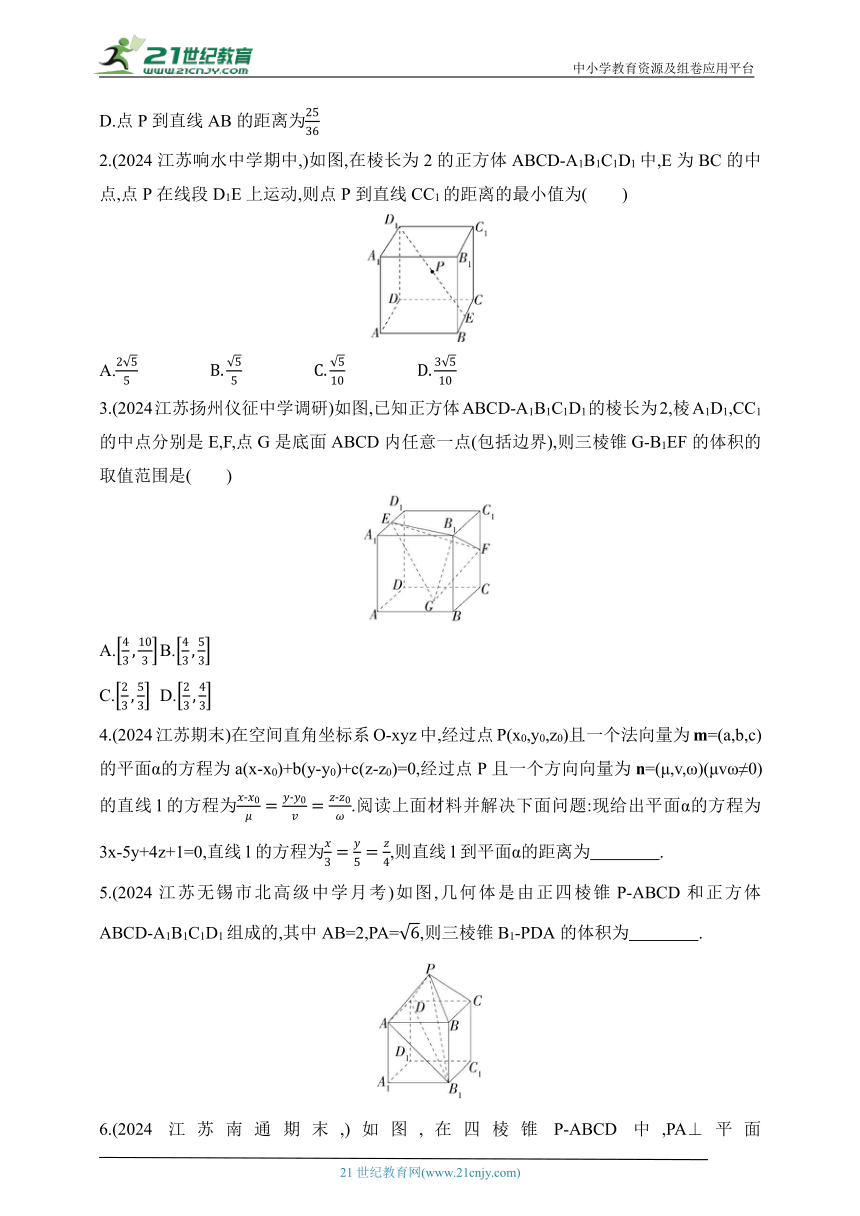
2.(2024江苏响水中学期中,)如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在线段D1E上运动,则点P到直线CC1的距离的最小值为( )
A.
3.(2024江苏扬州仪征中学调研)如图,已知正方体ABCD-A1B1C1D1的棱长为2,棱A1D1,CC1的中点分别是E,F,点G是底面ABCD内任意一点(包括边界),则三棱锥G-B1EF的体积的取值范围是( )
A. B.
C. D.
4.(2024江苏期末)在空间直角坐标系O-xyz中,经过点P(x0,y0,z0)且一个法向量为m=(a,b,c)的平面α的方程为a(x-x0)+b(y-y0)+c(z-z0)=0,经过点P且一个方向向量为n=(μ,v,ω)(μvω≠0)的直线l的方程为.阅读上面材料并解决下面问题:现给出平面α的方程为3x-5y+4z+1=0,直线l的方程为,则直线l到平面α的距离为 .
5.(2024江苏无锡市北高级中学月考)如图,几何体是由正四棱锥P-ABCD和正方体ABCD-A1B1C1D1组成的,其中AB=2,PA=,则三棱锥B1-PDA的体积为 .
6.(2024江苏南通期末,)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥AD,AD∥BC,AP=AB=AD=1,BC=2.
(1)求二面角B-PD-C的正弦值;
(2)在棱PC上确定一点E,使异面直线PD与BE所成角的大小为60°,并求此时点E到平面PBD的距离.
答案与分层梯度式解析
6.3.4 空间距离的计算
基础过关练
1.A 2.A 3.A 4.B 5.A
1.A 由题意可得=(0,1,2),
则|,
设向量u是直线AB的单位方向向量,则u=,
·u=(0,1,2)·,
则点C到直线AB的距离为.故选A.
2.A 如图所示,以A为坐标原点,AB,AD,AE所在直线分别为x轴、y轴、z轴建立空间直角坐标系,
则A(0,0,0),C(6,6,0),H(0,6,6),B(6,0,0),D(0,6,0),E(0,0,6),
所以=(-6,0,6),
因为=(1,2,5),所以P(1,2,5),所以=(-5,-4,5),
所以,
所以点P到直线CH的距离为=4.
故选A.
3.A 连接AG,由题意得OA,OB,OC互相垂直,以点O为原点,OA,OB,OC所在直线分别为x轴,y轴,z轴建立空间直角坐标系,如图,
则A(1,0,0),B(0,2,0),C(0,0,3),D(0,0,1),
由点G为△ABC的重心,得G,
所以=(-1,0,1),
所以|,
所以点G到直线AD的距离d=.故选A.
4.B ∵A(1,0,-1),B(0,-1,1),∴=(-1,-1,2),
又平面α的一个法向量为n=(1,2,1),
∴点A到平面α的距离为.故选B.
5.A 如图,以A为原点,AB,AD,AA1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,
则A(0,0,0),E(1,1,2),F(1,2,1),C(2,2,0),
所以=(2,2,0).
设平面AEF的一个法向量为n=(x,y,z),
则
令y=-1,得x=3,z=-1,所以n=(3,-1,-1),
故点C到平面AEF的距离为.故选A.
6.答案
解析 如图,以A为坐标原点,AB,AD,AA1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,
则A(0,0,0),C(1,1,0),N,
∴=(1,1,0),
设异面直线AM与CN的公垂线的方向向量为n=(x,y,z),则n⊥,n⊥,
∴n·x+z=0,n·z=0,
∴x=-2z,y=z,
取z=2,则x=-4,y=1,∴n=(-4,1,2),
∴异面直线AM与CN间的距离d=.
7.答案
解析 如图,以D为坐标原点建立空间直角坐标系,
则A(3,0,0),E(0,0,2),F(3,3,1),C1(0,3,3),B1(3,3,3),
所以=(-3,0,2),所以,
又因为AE 平面AB1E,FC1 平面AB1E,
所以FC1∥平面AB1E,
所以直线FC1到平面AB1E的距离即为点F到平面AB1E的距离.
设平面AB1E的一个法向量为n=(x,y,z),
则
令z=3,得x=2,y=-3,则n=(2,-3,3),
所以点F到平面AB1E的距离d=,故直线FC1到平面AB1E的距离为.
8.答案
解析 以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,
则A(4,0,0),M(2,0,4),B(4,4,0),E(0,2,4),F(2,4,4),N(4,2,4),∴=(0,4,0),
∴,∴EF∥MN,BF∥AM,
又EF 平面AMN,MN 平面AMN,∴EF∥平面AMN,同理得,BF∥平面AMN,又EF∩BF=F,EF,BF 平面EFBD,∴平面AMN∥平面EFBD.
∴平面AMN与平面EFBD间的距离即为点B到平面AMN的距离,
设平面AMN的一个法向量是n=(x,y,z),
则令z=1,则x=2,y=-2,
∴n=(2,-2,1).
∴平面AMN与平面EFBD间的距离d=.
9.解析 (1)证明:以A为原点,AD,AB,AA1所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,
则F(0,1,0),G(0,2,1),C1(2,2,2),A(0,0,0),B1(0,2,2),E(2,0,1),
则=(2,0,1),
设平面FGC1的一个法向量为m=(x,y,z),
则令z=2,则y=-2,x=-1,
所以m=(-1,-2,2).
设平面AB1E的一个法向量为n=(a,b,c),
则令c=2,则a=-1,b=-2,
所以n=(-1,-2,2).
所以m=n,所以平面FGC1∥平面AB1E.
(2)由(1)得=(2,0,1),
所以,即GC1∥AE,所以点C1到直线AE的距离即为直线GC1到直线AE的距离,
易知=(2,2,2),所以,所以直线GC1到直线AE的距离为.
(3)因为平面FGC1∥平面AB1E,GC1 平面FGC1,
所以GC1∥平面AB1E,
所以直线GC1到平面AB1E的距离等于点C1到平面AB1E的距离.
由(1)知=(-2,0,0),平面AB1E的一个法向量为n=(-1,-2,2),
所以点C1到平面AB1E的距离为,
所以直线GC1到平面AB1E的距离为.
能力提升练
1.AB 2.A 3.C
1.AB 以A为坐标原点建立空间直角坐标系,如图,
则A(0,0,0),B(1,0,0),D(0,1,0),A1(0,0,1),C1(1,1,1),D1(0,1,1),E,
所以=(0,1,-1),
设∠ABE=θ,则cos θ=,故sin θ =,
所以点A到直线BE的距离d1=||sin θ=1×,故A正确.
易知,平面ABC1D1的一个法向量为=(0,-1,1),
则点O到平面ABC1D1的距离d2=,故B正确.
设平面A1BD的一个法向量为n=(x,y,z),
则
令z=1,得x=1,y=1,则n=(1,1,1).
所以点D1到平面A1BD的距离d3=.
易知平面A1BD∥平面B1CD1,
所以平面A1BD与平面B1CD1间的距离等于点D1到平面A1BD的距离,
所以平面A1BD与平面B1CD1间的距离为,故C错误.
因为,所以,
易知=(1,0,0),
所以点P到直线AB的距离d4=,故D错误.故选AB.
2.A 以D为原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,
则E(1,2,0),D1(0,0,2),C(0,2,0),C1(0,2,2),
∴=(1,0,0).
解法一:设异面直线CC1与ED1的公垂线的方向向量为u=(x,y,z),则u⊥,u⊥,
则
令x=1,则y=-,z=0,∴u=,
∴异面直线D1E与CC1之间的距离d=,
∵点P在线段D1E上运动,
∴点P到直线CC1的距离的最小值为.
解法二:设P(x,y,z),,λ∈[0,1],则=(-λ,-2λ,2λ),则(x-1,y-2,z)=(-λ,-2λ,2λ),
所以
所以P(1-λ,2-2λ,2λ),
又C(0,2,0),∴=(1-λ,-2λ,2λ),
∴点P到直线CC1的距离d1=
=,
当且仅当λ=时,d1取最小值,为,∴点P到直线CC1的距离的最小值为.故选A.
3.C 以D为原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,如图所示,
则B1(2,2,2),E(1,0,2),F(0,2,1),
所以=(-1,-2,0),
则|,
取EF的中点M,连接B1M,则M,
所以,所以|,
易得B1E=B1F,则B1M⊥EF,
所以△B1EF的面积S=·EF·B1M=,
设平面B1EF的一个法向量为n=(x,y,z),
则
令x=2,得y=-1,z=-4,则n=(2,-1,-4),
设G(m,n,0)(0≤m≤2,0≤n≤2),
则=(2-m,2-n,2),
所以点G到平面B1EF的距离d=,
所以S·d=,
又-2≤2m-n≤4,所以,即.故选C.
4.答案
解析 由题可知点O(0,0,0)在直线l上,取平面α内一点P,则,由题意可得平面α的一个法向量为m=(3,-5,4),
所以cos<,m>=,
所以直线l到平面α的距离为|,m>|=.
5.答案 2
解析 连接AC,BD,且AC,BD相交于点O,连接PO,
易知PO⊥平面ABCD,
又AO 平面ABCD,所以PO⊥AO,
易得AO=,又PA=,所以PO==2.
以D1为坐标原点,的方向分别为x轴,y轴,z轴的正方向建立空间直角坐标系,如图所示,
则A(2,0,2),D(0,0,2),B1(2,2,0),P(1,1,4),
所以=(0,2,-2),
设平面PDA的一个法向量为n=(x,y,z),
则
令z=1,得x=0,y=-2,则n=(0,-2,1).
设B1到平面PDA的距离为d,
则d=.
在△PDA中,PA=PD=,AD=2,所以S△PDA=,
所以三棱锥B1-PDA的体积V=S△PDA·d==2.
6.解析 (1)以{}为单位正交基底,建立如图所示的空间直角坐标系,
则B(1,0,0),P(0,0,1),D(0,1,0),C(1,2,0),
所以=(1,1,0).
设平面PBD的一个法向量为n1=(x1,y1,z1),
则取x1=1,得n1=(1,1,1),
设平面PCD的一个法向量为n2=(x2,y2,z2),
则取x2=1,得n2=(1,-1,-1),
设二面角B-PD-C的平面角的大小为θ,
则|cos θ|=|cos|=,
所以sin θ=.
(2)由(1)知,=(1,2,-1),设(0<λ≤1),则=(λ,2λ,-λ),则=(λ-1,2λ,-λ+1).
因为异面直线PD与BE所成角的大小为60°,
所以cos 60°=|cos<,解得λ=或λ=0(舍去),
故,
由(1)知平面PBD的一个法向量为n1=(1,1,1),
所以点E到平面PBD的距离d=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025苏教版高中数学选择性必修第二册
6.3.4 空间距离的计算
基础过关练
题组一 点到直线的距离的计算
1.(2024江苏南通质量监测)在空间直角坐标系中,已知点A(1,1,1),B(0,1,0),C(1,2,3),则点C到直线AB的距离为( )
A. D.3
2.(2024安徽六安新安中学期中)如图,几何体ABCD-EFGH是棱长为6的正方体,若,则点P到直线CH的距离为( )
A.4 B.3 C.2 D.1
3.(2024江苏南京金陵中学检测)四面体OABC满足∠AOB=∠BOC=∠COA=90°,OA=1,OB=2,OC=3,点D在棱OC上,且OC=3OD,点G为△ABC的重心,则点G到直线AD的距离为( )
A.
题组二 点到平面的距离的计算
4.(2024江苏无锡太湖高级中学月考)已知平面α的一个法向量为n=(1,2,1),A(1,0,-1),B(0,-1,1),且A α,B∈α,则点A到平面α的距离为( )
A. D.1
5.(2023江苏常州武进检测)已知正方体ABCD-A1B1C1D1的棱长为2,E,F分别为上底面A1B1C1D1和侧面CDD1C1的中心,则点C到平面AEF的距离为( )
A.
题组三 直线与直线、直线与平面、平面与平面间的距离的计算
6.(2023湖北荆门月考)在棱长为1的正方体ABCD-A1B1C1D1中,M,N分别为棱A1B1,BB1的中点,则异面直线AM与CN间的距离为 .
7.(2024江苏无锡辅仁高级中学期中)在棱长为3的正方体ABCD-A1B1C1D1中,E为线段DD1靠近D1的三等分点,F为线段BB1靠近B的三等分点,则直线FC1到平面AB1E的距离为 .
8.如图所示,正方体ABCD-A1B1C1D1的棱长为4,M,N,E,F分别为A1D1,A1B1,C1D1,B1C1的中点,则平面AMN与平面EFBD间的距离为 .
9.(2024河南新高中创新联盟TOP二十名校月考)如图,在棱长为2的正方体ABCD-A1B1C1D1中,E,F,G分别是线段DD1,AB,BB1的中点.
(1)求证:平面FGC1∥平面AB1E;
(2)求直线GC1到直线AE的距离;
(3)求直线GC1到平面AB1E的距离.
能力提升练
题组 空间距离的计算及应用
1.(多选题)(2024安徽南陵中学一诊)已知正方体ABCD-A1B1C1D1的棱长为1,E,O分别是A1B1,A1C1的中点,点P满足,则下列说法正确的是( )
A.点A到直线BE的距离是
B.点O到平面ABC1D1的距离为
C.平面A1BD与平面B1CD1间的距离为
D.点P到直线AB的距离为
2.(2024江苏响水中学期中,)如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在线段D1E上运动,则点P到直线CC1的距离的最小值为( )
A.
3.(2024江苏扬州仪征中学调研)如图,已知正方体ABCD-A1B1C1D1的棱长为2,棱A1D1,CC1的中点分别是E,F,点G是底面ABCD内任意一点(包括边界),则三棱锥G-B1EF的体积的取值范围是( )
A. B.
C. D.
4.(2024江苏期末)在空间直角坐标系O-xyz中,经过点P(x0,y0,z0)且一个法向量为m=(a,b,c)的平面α的方程为a(x-x0)+b(y-y0)+c(z-z0)=0,经过点P且一个方向向量为n=(μ,v,ω)(μvω≠0)的直线l的方程为.阅读上面材料并解决下面问题:现给出平面α的方程为3x-5y+4z+1=0,直线l的方程为,则直线l到平面α的距离为 .
5.(2024江苏无锡市北高级中学月考)如图,几何体是由正四棱锥P-ABCD和正方体ABCD-A1B1C1D1组成的,其中AB=2,PA=,则三棱锥B1-PDA的体积为 .
6.(2024江苏南通期末,)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥AD,AD∥BC,AP=AB=AD=1,BC=2.
(1)求二面角B-PD-C的正弦值;
(2)在棱PC上确定一点E,使异面直线PD与BE所成角的大小为60°,并求此时点E到平面PBD的距离.
答案与分层梯度式解析
6.3.4 空间距离的计算
基础过关练
1.A 2.A 3.A 4.B 5.A
1.A 由题意可得=(0,1,2),
则|,
设向量u是直线AB的单位方向向量,则u=,
·u=(0,1,2)·,
则点C到直线AB的距离为.故选A.
2.A 如图所示,以A为坐标原点,AB,AD,AE所在直线分别为x轴、y轴、z轴建立空间直角坐标系,
则A(0,0,0),C(6,6,0),H(0,6,6),B(6,0,0),D(0,6,0),E(0,0,6),
所以=(-6,0,6),
因为=(1,2,5),所以P(1,2,5),所以=(-5,-4,5),
所以,
所以点P到直线CH的距离为=4.
故选A.
3.A 连接AG,由题意得OA,OB,OC互相垂直,以点O为原点,OA,OB,OC所在直线分别为x轴,y轴,z轴建立空间直角坐标系,如图,
则A(1,0,0),B(0,2,0),C(0,0,3),D(0,0,1),
由点G为△ABC的重心,得G,
所以=(-1,0,1),
所以|,
所以点G到直线AD的距离d=.故选A.
4.B ∵A(1,0,-1),B(0,-1,1),∴=(-1,-1,2),
又平面α的一个法向量为n=(1,2,1),
∴点A到平面α的距离为.故选B.
5.A 如图,以A为原点,AB,AD,AA1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,
则A(0,0,0),E(1,1,2),F(1,2,1),C(2,2,0),
所以=(2,2,0).
设平面AEF的一个法向量为n=(x,y,z),
则
令y=-1,得x=3,z=-1,所以n=(3,-1,-1),
故点C到平面AEF的距离为.故选A.
6.答案
解析 如图,以A为坐标原点,AB,AD,AA1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,
则A(0,0,0),C(1,1,0),N,
∴=(1,1,0),
设异面直线AM与CN的公垂线的方向向量为n=(x,y,z),则n⊥,n⊥,
∴n·x+z=0,n·z=0,
∴x=-2z,y=z,
取z=2,则x=-4,y=1,∴n=(-4,1,2),
∴异面直线AM与CN间的距离d=.
7.答案
解析 如图,以D为坐标原点建立空间直角坐标系,
则A(3,0,0),E(0,0,2),F(3,3,1),C1(0,3,3),B1(3,3,3),
所以=(-3,0,2),所以,
又因为AE 平面AB1E,FC1 平面AB1E,
所以FC1∥平面AB1E,
所以直线FC1到平面AB1E的距离即为点F到平面AB1E的距离.
设平面AB1E的一个法向量为n=(x,y,z),
则
令z=3,得x=2,y=-3,则n=(2,-3,3),
所以点F到平面AB1E的距离d=,故直线FC1到平面AB1E的距离为.
8.答案
解析 以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,
则A(4,0,0),M(2,0,4),B(4,4,0),E(0,2,4),F(2,4,4),N(4,2,4),∴=(0,4,0),
∴,∴EF∥MN,BF∥AM,
又EF 平面AMN,MN 平面AMN,∴EF∥平面AMN,同理得,BF∥平面AMN,又EF∩BF=F,EF,BF 平面EFBD,∴平面AMN∥平面EFBD.
∴平面AMN与平面EFBD间的距离即为点B到平面AMN的距离,
设平面AMN的一个法向量是n=(x,y,z),
则令z=1,则x=2,y=-2,
∴n=(2,-2,1).
∴平面AMN与平面EFBD间的距离d=.
9.解析 (1)证明:以A为原点,AD,AB,AA1所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,
则F(0,1,0),G(0,2,1),C1(2,2,2),A(0,0,0),B1(0,2,2),E(2,0,1),
则=(2,0,1),
设平面FGC1的一个法向量为m=(x,y,z),
则令z=2,则y=-2,x=-1,
所以m=(-1,-2,2).
设平面AB1E的一个法向量为n=(a,b,c),
则令c=2,则a=-1,b=-2,
所以n=(-1,-2,2).
所以m=n,所以平面FGC1∥平面AB1E.
(2)由(1)得=(2,0,1),
所以,即GC1∥AE,所以点C1到直线AE的距离即为直线GC1到直线AE的距离,
易知=(2,2,2),所以,所以直线GC1到直线AE的距离为.
(3)因为平面FGC1∥平面AB1E,GC1 平面FGC1,
所以GC1∥平面AB1E,
所以直线GC1到平面AB1E的距离等于点C1到平面AB1E的距离.
由(1)知=(-2,0,0),平面AB1E的一个法向量为n=(-1,-2,2),
所以点C1到平面AB1E的距离为,
所以直线GC1到平面AB1E的距离为.
能力提升练
1.AB 2.A 3.C
1.AB 以A为坐标原点建立空间直角坐标系,如图,
则A(0,0,0),B(1,0,0),D(0,1,0),A1(0,0,1),C1(1,1,1),D1(0,1,1),E,
所以=(0,1,-1),
设∠ABE=θ,则cos θ=,故sin θ =,
所以点A到直线BE的距离d1=||sin θ=1×,故A正确.
易知,平面ABC1D1的一个法向量为=(0,-1,1),
则点O到平面ABC1D1的距离d2=,故B正确.
设平面A1BD的一个法向量为n=(x,y,z),
则
令z=1,得x=1,y=1,则n=(1,1,1).
所以点D1到平面A1BD的距离d3=.
易知平面A1BD∥平面B1CD1,
所以平面A1BD与平面B1CD1间的距离等于点D1到平面A1BD的距离,
所以平面A1BD与平面B1CD1间的距离为,故C错误.
因为,所以,
易知=(1,0,0),
所以点P到直线AB的距离d4=,故D错误.故选AB.
2.A 以D为原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,
则E(1,2,0),D1(0,0,2),C(0,2,0),C1(0,2,2),
∴=(1,0,0).
解法一:设异面直线CC1与ED1的公垂线的方向向量为u=(x,y,z),则u⊥,u⊥,
则
令x=1,则y=-,z=0,∴u=,
∴异面直线D1E与CC1之间的距离d=,
∵点P在线段D1E上运动,
∴点P到直线CC1的距离的最小值为.
解法二:设P(x,y,z),,λ∈[0,1],则=(-λ,-2λ,2λ),则(x-1,y-2,z)=(-λ,-2λ,2λ),
所以
所以P(1-λ,2-2λ,2λ),
又C(0,2,0),∴=(1-λ,-2λ,2λ),
∴点P到直线CC1的距离d1=
=,
当且仅当λ=时,d1取最小值,为,∴点P到直线CC1的距离的最小值为.故选A.
3.C 以D为原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,如图所示,
则B1(2,2,2),E(1,0,2),F(0,2,1),
所以=(-1,-2,0),
则|,
取EF的中点M,连接B1M,则M,
所以,所以|,
易得B1E=B1F,则B1M⊥EF,
所以△B1EF的面积S=·EF·B1M=,
设平面B1EF的一个法向量为n=(x,y,z),
则
令x=2,得y=-1,z=-4,则n=(2,-1,-4),
设G(m,n,0)(0≤m≤2,0≤n≤2),
则=(2-m,2-n,2),
所以点G到平面B1EF的距离d=,
所以S·d=,
又-2≤2m-n≤4,所以,即.故选C.
4.答案
解析 由题可知点O(0,0,0)在直线l上,取平面α内一点P,则,由题意可得平面α的一个法向量为m=(3,-5,4),
所以cos<,m>=,
所以直线l到平面α的距离为|,m>|=.
5.答案 2
解析 连接AC,BD,且AC,BD相交于点O,连接PO,
易知PO⊥平面ABCD,
又AO 平面ABCD,所以PO⊥AO,
易得AO=,又PA=,所以PO==2.
以D1为坐标原点,的方向分别为x轴,y轴,z轴的正方向建立空间直角坐标系,如图所示,
则A(2,0,2),D(0,0,2),B1(2,2,0),P(1,1,4),
所以=(0,2,-2),
设平面PDA的一个法向量为n=(x,y,z),
则
令z=1,得x=0,y=-2,则n=(0,-2,1).
设B1到平面PDA的距离为d,
则d=.
在△PDA中,PA=PD=,AD=2,所以S△PDA=,
所以三棱锥B1-PDA的体积V=S△PDA·d==2.
6.解析 (1)以{}为单位正交基底,建立如图所示的空间直角坐标系,
则B(1,0,0),P(0,0,1),D(0,1,0),C(1,2,0),
所以=(1,1,0).
设平面PBD的一个法向量为n1=(x1,y1,z1),
则取x1=1,得n1=(1,1,1),
设平面PCD的一个法向量为n2=(x2,y2,z2),
则取x2=1,得n2=(1,-1,-1),
设二面角B-PD-C的平面角的大小为θ,
则|cos θ|=|cos
所以sin θ=.
(2)由(1)知,=(1,2,-1),设(0<λ≤1),则=(λ,2λ,-λ),则=(λ-1,2λ,-λ+1).
因为异面直线PD与BE所成角的大小为60°,
所以cos 60°=|cos<,解得λ=或λ=0(舍去),
故,
由(1)知平面PBD的一个法向量为n1=(1,1,1),
所以点E到平面PBD的距离d=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
