2025苏教版高中数学选择性必修第二册强化练习题(含解析)--第6章 空间向量与立体几何拔高练
文档属性
| 名称 | 2025苏教版高中数学选择性必修第二册强化练习题(含解析)--第6章 空间向量与立体几何拔高练 |

|
|
| 格式 | docx | ||
| 文件大小 | 837.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-15 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025苏教版高中数学选择性必修第二册
综合拔高练
五年高考练
考点1 用空间向量判定、证明平行与垂直
1.(2022全国乙理,7)在正方体ABCD-A1B1C1D1中,E,F分别为AB,BC的中点,则( )
A.平面B1EF⊥平面BDD1
B.平面B1EF⊥平面A1BD
C.平面B1EF∥平面A1AC
D.平面B1EF∥平面A1C1D
2.(2023全国乙理,19)如图,在三棱锥P-ABC中,AB⊥BC,AB=2,BC=2,BP,AP,BC的中点分别为D,E,O,AD=DO,点F在AC上,BF⊥AO.
(1)证明:EF∥平面ADO;
(2)证明:平面ADO⊥平面BEF;
(3)求二面角D-AO-C的正弦值.
考点2 用空间向量求解空间角问题
3.(2022全国甲理,18)在四棱锥P-ABCD中,PD⊥底面ABCD,CD∥AB,AD=DC=CB=1,AB=2,DP=.
(1)证明:BD⊥PA;
(2)求PD与平面PAB所成的角的正弦值.
4.(2024新课标Ⅰ,17)如图,四棱锥P-ABCD中,PA⊥底面ABCD,PA=AC=2,BC=1,AB=.
(1)若AD⊥PB,证明:AD∥平面PBC;
(2)若AD⊥DC,且二面角A-CP-D的正弦值为,求AD.
5.(2024新课标Ⅱ,17)如图,平面四边形ABCD中,AB=8,CD=3,AD=5,∠ADC=90°,∠BAD=30°,点E,F满足.将△AEF沿EF翻折至△PEF,使得PC=4.
(1)证明:EF⊥PD;
(2)求面PCD与面PBF所成的二面角的正弦值.
考点3 用空间向量求解空间距离
6.(2023全国甲理,18)如图,在三棱柱ABC-A1B1C1中,A1C⊥平面ABC,∠ACB=90°,AA1=2,A1到平面BCC1B1的距离为1.
(1)证明:A1C=AC;
(2)已知AA1与BB1的距离为2,求AB1与平面BCC1B1所成角的正弦值.
7.(2024天津,17)已知四棱柱ABCD-A1B1C1D1中,底面ABCD为梯形,AB∥CD,A1A⊥平面ABCD,AD⊥AB,其中AB=AA1=2,AD=DC=1.N是B1C1的中点,M是DD1的中点.
(1)求证:D1N∥平面CB1M;
(2)求平面CB1M与平面BB1C1C的夹角余弦值;
(3)求点B到平面CB1M的距离.
考点4 用空间向量解决立体几何中的最值问题
8.(2021全国甲理,19)已知直三棱柱ABC-A1B1C1中,侧面AA1B1B为正方形,AB=BC=2,E,F分别为AC和CC1的中点,D为棱A1B1上的点,BF⊥A1B1.
(1)证明:BF⊥DE;
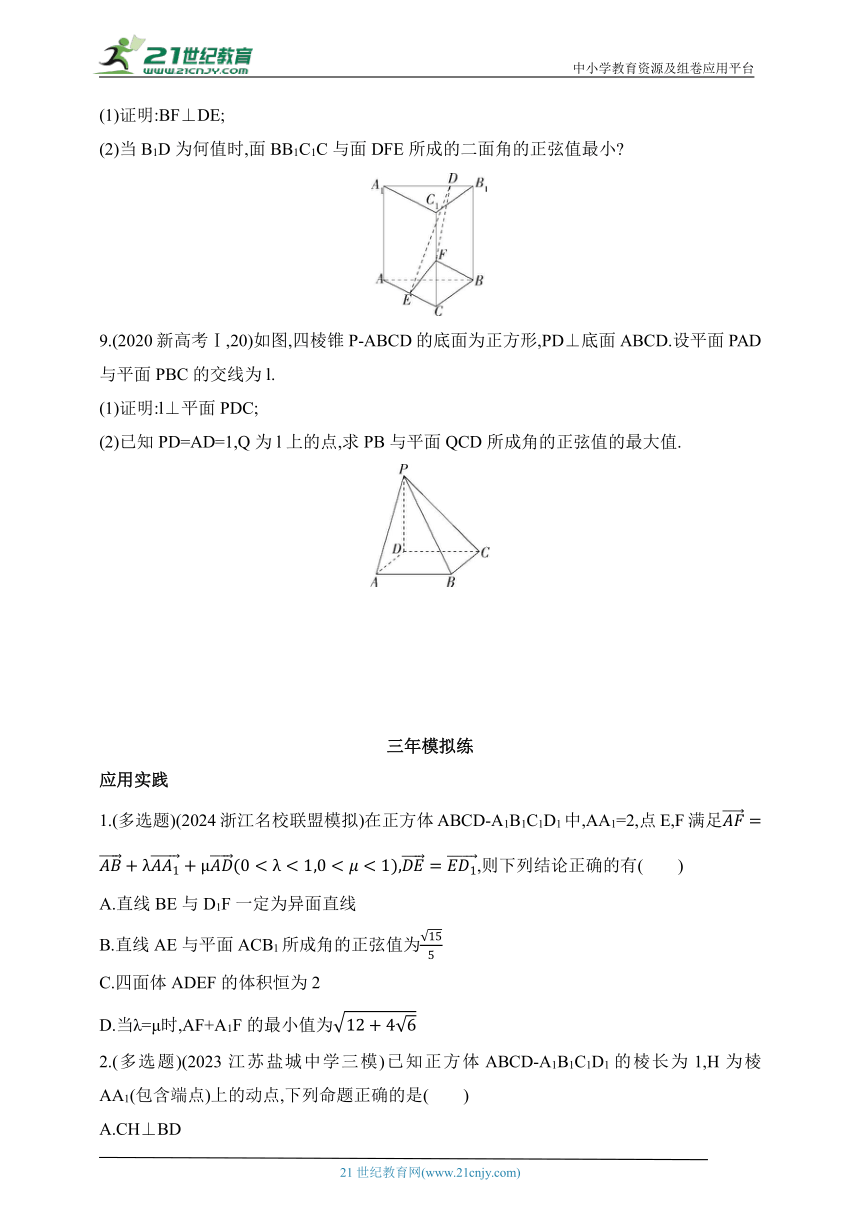
(2)当B1D为何值时,面BB1C1C与面DFE所成的二面角的正弦值最小
9.(2020新高考Ⅰ,20)如图,四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD.设平面PAD与平面PBC的交线为l.
(1)证明:l⊥平面PDC;
(2)已知PD=AD=1,Q为l上的点,求PB与平面QCD所成角的正弦值的最大值.
三年模拟练
应用实践
1.(多选题)(2024浙江名校联盟模拟)在正方体ABCD-A1B1C1D1中,AA1=2,点E,F满足,则下列结论正确的有( )
A.直线BE与D1F一定为异面直线
B.直线AE与平面ACB1所成角的正弦值为
C.四面体ADEF的体积恒为2
D.当λ=μ时,AF+A1F的最小值为
2.(多选题)(2023江苏盐城中学三模)已知正方体ABCD-A1B1C1D1的棱长为1,H为棱AA1(包含端点)上的动点,下列命题正确的是( )
A.CH⊥BD
B.二面角D1-AB1-C的平面角的大小为
C.点H到平面CB1D1的距离的取值范围是
D.若CH⊥平面β,则直线CD与平面β所成角的正弦值的取值范围为
3.(多选题)(2023江苏扬州期末)如图,正方体ABCD-A1B1C1D1的棱长为2,E为线段A1D1的中点,F为线段CC1上的一个动点,则下列说法正确的是( )
A.当F为CC1的中点时,点B1到平面AEF的距离为
B.当F为CC1的中点时,记DB1与平面AEF的交点为M,则DM=DB1
C.存在点F,使得异面直线DB1与BF所成的角为45°
D.存在点F,使得点F到直线AE的距离为
4.(2023江苏镇江中学三模)如图,四边形ABCD是边长为2的菱形,∠ABC=60°,四边形PACQ为矩形,PA=1,从下列三个条件中任选一个作为已知条件,并解答问题.
①BP,DP与平面ABCD所成的角相等;②三棱锥P-ABD的体积为;③cos∠BPA=.
(1)证明:平面PACQ⊥平面ABCD;
(2)求二面角B-PQ-D的大小;
(3)求点C到平面BPQ的距离.
5.(2024江苏镇江中学检测)如图,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,O为BD的中点,△OCD是边长为1的等边三角形,且VA-BCD=.
(1)证明:OA⊥CD;
(2)求直线CD与平面ABC所成角的正弦值;
(3)在棱AD上是否存在点E,使得二面角E-BC-D的大小为45° 若存在,求出的值;若不存在,请说明理由.
迁移创新
6.(2023上海南洋模范中学期末)《瀑布》(图1)是为人所熟知的作品之一,图中的瀑布会源源不断地落下,落下的水又逆流而上,荒唐至极,但又会让你百看不腻,画面下方还有一位饶有兴致的观察者,似乎她没发现什么不对劲.画面两座高塔上各有一个几何体,左塔上方是著名的“三立方体合体”,它由三个正方体构成,右塔上的几何体是首次出现,后称“埃舍尔多面体”.
图1
埃舍尔多面体可以用两两垂直且中心重合的三个正方形构造,设边长均为2,定义正方形AnBnCnDn,n=1,2,3的顶点为“框架点”,定义两正方形交线为“极轴”,其端点为“极点”,记为Pn,Qn,将极点P1,Q1分别与正方形A2B2C2D2的顶点连线,取其中点记为Em,Fm,m=1,2,3,4(如图2).埃舍尔多面体可视部分是由12个四棱锥构成的,这些四棱锥顶点均为“框架点”,底面四边形由两个“极点”与两个“中点”构成,为了便于理解,图3中我们构造了其中两个四棱锥A1-P1E1P2E2和A2-P2E1P3F1.
(1)求异面直线P1A2与Q1B2所成角的余弦值;
(2)求平面P1A1E1与平面A1E2P2所成的锐二面角的正弦值;
(3)求埃舍尔多面体的表面积与体积(直接写出答案).
图2
图3
答案与分层梯度式解析
综合拔高练
五年高考练
1.A 如图,以D为坐标原点,建立空间直角坐标系D-xyz,设AB=2,
则B1(2,2,2),E(2,1,0),D(0,0,0),F(1,2,0),B(2,2,0),A1(2,0,2),A(2,0,0),C(0,2,0),C1(0,2,2),
所以=(-2,2,0),
设平面B1EF的一个法向量为m=(x,y,z),
则
令x=2,则y=2,z=-1,
所以m=(2,2,-1),
因为平面BDD1的一个法向量为=(-2,2,0),
且·m=-2×2+2×2+(-1)×0=0,
所以⊥m,所以平面B1EF⊥平面BDD1,故A正确;
同理可得,平面A1BD的一个法向量为n1=(1,-1,-1),平面A1AC的一个法向量为n2=(1,1,0),平面A1C1D的一个法向量为n3=(1,1,-1),
因为m·n1=2-2+1=1≠0,所以平面B1EF与平面A1BD不垂直,故B错误;
因为m与n2不平行,所以平面B1EF与平面A1AC不平行,
故C错误;
因为m与n3不平行,所以平面B1EF与平面A1C1D不平行,故D错误.
故选A.
高考风向 空间直线、平面的位置关系是高考的高频考点,证明平行与垂直的常用方法是几何法和坐标法,利用几何法解题的关键是熟练掌握三种平行关系、三种垂直关系的转化和作出恰当的辅助线;利用坐标法解题的关键是直线的方向向量、平面的法向量间的位置关系,即向量运算.要注意结合图形灵活选择恰当的方法,利用坐标法证明或求解时,要避免运算错误.本题以正方体为载体,证明面面平行、面面垂直,体现了试题的基础性和综合性.
2.解析 以BA,BC所在直线分别为x轴,y轴,垂直于平面ABC的直线为z轴,建立如图2所示的空间直角坐标系,
则B(0,0,0),A(2,0,0),O(0,,0).
(1)证明:设AF=λAC,0<λ<1.
由得F(2-2λ,2λ,0),
∴λ,0),
又,0),BF⊥AO,
∴=0,即-2(2-2λ)+4λ=0,解得λ=,
故F为AC的中点.
又D,E,O分别为PB,PA,BC的中点,
∴DO∥PC,EF∥PC,
∴DO∥EF,
又EF 平面ADO,DO 平面ADO,
∴EF∥平面ADO.
(2)证明:∵D,O分别是PB,BC的中点,且PC=,
∴DO=,又AD=.
由cos∠ABD=,得PA=.
设P(x,y,z),z>0,则由PB=PC=(z>0),
解得故P(-1,),
又∵D,E分别是PB,PA的中点,
∴D,
∴,
又,0),
∴=0,
∴,即AO⊥BE,
又AO⊥BF,BE∩BF=B,BE、BF 平面BEF,
∴AO⊥平面BEF,又AO 平面ADO,
∴平面ADO⊥平面BEF.
(3)易知平面AOC的一个法向量为m1=(0,0,1),
由(2)知,
设平面AOD的一个法向量为m2=(x1,y1,z1),则
即
取x1=1,则y1=,
则m2=(1,),
设二面角D-AO-C的平面角的大小为θ,则|cos θ|=
|cos|=.
∴sin θ=,
即二面角D-AO-C的正弦值为.
3.解析 以D为原点,DC,DP所在直线分别为y轴,z轴,过D点且垂直于AB的直线为x轴,建立空间直角坐标系,如图.
(1)证明:结合题意知D(0,0,0),B,
则,
∴+0=0,
∴,∴BD⊥PA.
(2)设平面PAB的一个法向量为m=(x,y,z),
由(1)知=(0,2,0),
∴
则y=0,令z=1,则x=2,故m=(2,0,1).
又∵),
∴PD与平面PAB所成的角的正弦值等于|cos<,m>|=.
高考风向 求直线与平面所成的角是高考中常见的一种问题.线面角求解的常用方法是坐标法和几何法.利用坐标法解题的关键是求出平面法向量及直线的方向向量的坐标,本题的条件中含有线面垂直,有利于建立空间直角坐标系,进而通过坐标法求线面角的正弦值.利用坐标法求线面角,本质是把几何关系转化为向量运算.利用坐标法解决问题时,要防止运算错误.
4.解析 (1)证明:在△ABC中,AB=,BC=1,AC=2,
故有AB2+BC2=AC2,所以AB⊥BC.
因为PA⊥底面ABCD,AD 平面ABCD,
所以PA⊥AD,
又因为AD⊥PB,PB∩PA=P,PB,PA 平面PAB,
所以AD⊥平面PAB,又AB 平面PAB,
所以AD⊥AB,
又因为AB⊥BC,A,B,C,D在同一平面内,
所以AD∥BC.
又因为BC 平面PBC,AD 平面PBC,
所以AD∥平面PBC.
(2)因为AD⊥DC,所以以DA,DC所在直线分别为x轴,y轴,过D作与PA平行的直线为z轴,建立空间直角坐标系,如图,
则D(0,0,0),
设AD=m(m>0),则DC=,0).
,0),
设平面ACP的一个法向量为n1=(x1,y1,z1),
则
即不妨取x1=,
则n1=(,m,0).
设平面DCP的一个法向量为n2=(x2,y2,z2),
则
易知y2=0,不妨取z2=m,
则x2=-2,故n2=(-2,0,m).
因为二面角A-CP-D的正弦值为,
所以|cos|=,
解得m=(舍负),
所以AD=.
5.解析 (1)证明:由题知AE=AB=4,∠FAE=30°,
∴EF==2,
∴EF2+AE2=AF2,∴AE⊥EF,
∴EF⊥PE,又PE∩AE=E,PE,AE 平面PED,∴EF⊥平面PED,又PD 平面PED,∴EF⊥PD.
(2)连接EC,∵CD=3,DE=AD-AE=3,∠ADC=90°,∴EC==6,
又PE=AE=2,∴EC2+PE2=PC2,∴PE⊥EC,又PE⊥EF,EC∩EF=E,EC,EF 平面ABCD,
∴PE⊥平面ABCD,
又ED 平面ABCD,∴PE⊥ED,又PE⊥EF,EF⊥ED,
∴PE,EF,ED两两垂直,
∴以E为原点,EF,ED,EP所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,如图,
则A(0,-2),
∴,0),
=(3,0,0).
设m=(x1,y1,z1),n=(x2,y2,z2)分别为平面PBF,平面PCD的一个法向量,
∴
令x1=,则m=(,-1,1),令y2=2,则n=(0,2,3).
∴cos=,
∴sin=,
∴所求正弦值为.
6.解析 (1)证明:∵A1C⊥平面ABC,BC 平面ABC,∴A1C⊥BC.
∵∠ACB=90°,∴AC⊥BC.
又AC∩A1C=C,AC,A1C 平面AA1C1C,
∴BC⊥平面AA1C1C.
又∵BC 平面BCC1B1,
∴平面BCC1B1⊥平面AA1C1C.
过A1作A1H⊥CC1,垂足为H,又平面BCC1B1⊥平面AA1C1C,平面BCC1B1∩平面AA1C1C=CC1,A1H 平面AA1C1C,
∴A1H⊥平面BCC1B1,
∴A1H=1.
易知∠CA1C1=90°,在Rt△A1CC1中,CC1=2=2A1H,
∴H为CC1的中点,
∴△A1CC1为等腰直角三角形,
∴A1C=A1C1.
易知AC A1C1,∴A1C=AC.
(2)以C为坐标原点,CA,CB,CA1所在直线分别为x轴,y轴,z轴建立空间直角坐标系.在平面BCC1B1内,过H作HQ∥BC,交BB1于点Q,连接A1Q,如图.
易知CC1⊥A1H,CC1⊥HQ,CC1 BB1,又A1H∩HQ=H,A1H,HQ 平面A1HQ,∴CC1⊥平面A1HQ,BB1⊥平面A1HQ,又A1Q 平面A1HQ,∴BB1⊥A1Q,∴A1Q=2,∴在Rt△A1HQ中,HQ=.
易知A1C=AC=,则A().
设平面BCC1B1的一个法向量为n=(x,y,z),
则取x=1,得n=(1,0,1).
设直线AB1与平面BCC1B1所成的角为θ,
则sin θ=|cos<,n>|==
.
∴AB1与平面BCC1B1所成角的正弦值为.
7.解析 (1)证明:取B1C的中点P,连接NP,MP,
又N为B1C1的中点,
所以在△B1CC1中,NP∥CC1,NP=CC1,
因为M是DD1的中点,DD1∥CC1,
所以D1M=CC1,且D1M∥CC1,
则有D1M∥NP,D1M=NP,故四边形D1MPN是平行四边形,
所以D1N∥MP,又MP 平面CB1M,D1N 平面CB1M,
所以D1N∥平面CB1M.
(2)已知A1A⊥平面ABCD,AD⊥AB,所以以A为原点,建立如图所示的空间直角坐标系,
易知AB=AA1=2,AD=DC=1,
则B(2,0,0),C(1,1,0),B1(2,0,2),M(0,1,1),
所以=(0,0,2).
设平面CB1M与平面BB1C1C的一个法向量分别为m=(x1,y1,z1),n=(x2,y2,z2).
则
则z2=0.分别取x1=1,x2=1,得y1=3,z1=1,y2=1,
所以m=(1,3,1),n=(1,1,0),
则|cos|=,
故平面CB1M与平面BB1C1C夹角的余弦值为.
(3)由(2)知=(0,0,2),平面CB1M的一个法向量为m=(1,3,1),
则,
即点B到平面CB1M的距离为.
8.解析 ∵BF⊥A1B1,B1B⊥A1B1,BF∩B1B=B,BF 平面B1C1CB,BB1 平面B1C1CB,∴A1B1⊥平面B1C1CB.
∵AB∥A1B1,∴AB⊥平面B1C1CB,
又∵BC 平面B1C1CB,∴AB⊥BC.
以B为坐标原点,BA,BC,BB1所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系,
则B(0,0,0),F(0,2,1),E(1,1,0),
∴=(0,2,1),设B1D=a(0≤a≤2),则D(a,0,2),
∴=(1-a,1,-2).
(1)证明:∵=(0,2,1)·(1-a,1,-2)=0×(1-a)+2×1+1×(-2)=0,
∴BF⊥DE.
(2)=(a,-2,1),
设平面DFE的一个法向量为n=(x,y,z),
则
不妨设x=1,则y=,
∴n=.
易知m=(1,0,0)是平面BB1C1C的一个法向量.
设平面BB1C1C与平面DEF所成的锐二面角的大小为θ,
则cos θ=|cos|=
=
=,∴sin θ=,
故当a=,即B1D=时,平面BB1C1C与平面DFE所成的二面角的正弦值最小,最小值为.
解题反思 (1)证明线线垂直常用的方法是先证明线面垂直,也可以通过计算两直线的方向向量的数量积为0证明,即“以算代证”.
(2)求解最大值、最小值以及取值范围问题时,通常建立目标函数,通过求函数的最值或值域解决,本题建立空间直角坐标系,在题中设出B1D=a(0≤a≤2),得D(a,0,2),通过平面与平面所成的锐二面角的余弦值最大,求得正弦值最小是关键一步.
9.解析 (1)证明:因为PD⊥底面ABCD,所以PD⊥AD.因为底面ABCD为正方形,所以AD⊥DC.又DC∩PD=D,DC,PD 平面PDC,所以AD⊥平面PDC.
因为AD∥BC,AD 平面PBC,所以AD∥平面PBC.
由已知得l∥AD,
因此l⊥平面PDC.
(2)以D为坐标原点,的方向分别为x轴,y轴,z轴的正方向,建立空间直角坐标系D-xyz(图略),则D(0,0,0),C(0,1,0),B(1,1,0),P(0,0,1),
所以=(1,1,-1).
由(1)可设Q(a,0,1),则=(a,0,1).
设平面QCD的一个法向量是n=(x,y,z),
则
取x=-1,
则n=(-1,0,a).
所以cos设PB与平面QCD所成的角为θ,
则sin θ=.
因为,当且仅当a=1时等号成立,所以PB与平面QCD所成角的正弦值的最大值为.
三年模拟练
1.ABD 2.ACD 3.ABD
1.ABD 以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,如图1,
则A(2,0,0),B(2,2,0),C(0,2,0),D(0,0,0),A1(2,0,2),B1(2,2,2),E(0,0,1),
所以=(-2,0,0).
由(0<λ<1,0<μ<1)得=(-2μ,2,2λ),所以F(2-2μ,2,2λ).
由于0<λ<1,0<μ<1,所以0<2-2μ<2,0<2λ<2,所以点F在平面BCC1B1内(不包括边界),连接BD,B1D1,又D1在平面BB1D1D内,所以D1F和平面BB1D1D相交,
又BE 平面BB1D1D,D1 直线BE,所以直线BE与D1F一定为异面直线,故A正确.
易得=(-2,0,1).
设平面ACB1的一个法向量为m=(x,y,z),
则
令y=1,得x=1,z=-1,则m=(1,1,-1),
所以cos<,m>=,
设直线AE与平面ACB1所成的角为θ,θ∈,
则sin θ=|cos<,m>|=,故B正确.
因为点F在平面BCC1B1内(不包括边界),所以点F到平面ADE的距离为2,所以V四面体ADEF=,故C错误.
当λ=μ时,F(2-2λ,2,2λ),连接BC1,则点F在BC1上(不含端点).
连接A1B,A1C1,将平面A1BC1绕BC1翻折到与平面ABC1D1在同一平面内,如图2,
连接AA1,此时AA1与BC1的交点即为当λ=μ时,使AF+A1F取最小值的点F.
由题意可知AB=2,A1B=2,∠ABA1=,
所以A=AB2+A1B2-2AB·A1Bcos∠ABA1=22+(2×cos ,
所以AA1=,
所以AF+A1F的最小值为,故D正确.
故选ABD.
2.ACD 以D为坐标原点建立如图所示的空间直角坐标系,
则D(0,0,0),B(1,1,0),C(0,1,0),A(1,0,0),D1(0,0,1),C1(0,1,1),B1(1,1,1),
设H(1,0,h),0≤h≤1.
对于A,=(1,1,0),则=0,即CH⊥BD,故A正确.
对于B,=(-1,1,0),
设平面AB1D1的一个法向量为m=(x,y,z),
则
令z=1,得x=1,y=-1,则m=(1,-1,1).
设平面AB1C的一个法向量为n=(a,b,c),
则
令b=1,得a=1,c=-1,则n=(1,1,-1).
故cos=,
由图可知,二面角D1-AB1-C为锐二面角,故其余弦值为,故二面角D1-AB1-C的平面角的大小不是,故B错误.
对于C,=(0,1,-1),
设平面CB1D1的一个法向量为k=(p,q,r),
则
令q=1,得p=-1,r=1,则k=(-1,1,1).
又=(0,-1,h-1),
∴点H到平面CB1D1的距离为||·,故C正确.
对于D,设直线CD与平面β所成的角为θ.
∵CH⊥平面β,∴=(1,-1,h)为平面β的一个法向量,
又=(0,1,0),∴sin θ=|cos<,
又h∈[0,1],∴,故D正确.
故选ACD.
方法总结 对于空间中位置关系的判断、角的计算或取值范围的求解问题,可结合几何体的结构特征建立合适的空间直角坐标系,通过向量的共线、向量的数量积等来判断位置关系,通过平面的法向量、直线的方向向量等来处理相关角的计算或取值范围的求解问题.
3.ABD 如图,以D为坐标原点建立空间直角坐标系,
则D(0,0,0),A(2,0,0),E(1,0,2),B1(2,2,2),B(2,2,0),
当F为CC1的中点时,F(0,2,1),
对于A,易得=(-2,2,1),
设平面AEF的一个法向量为m=(x,y,z),则
令z=1,得x=2,y=,则m=,
又=(0,2,2),
所以点B1到平面AEF的距离为,故A正确;
对于B,设(0≤λ≤1),则M(2λ,2λ,2λ),
又点M在平面AEF内,则,即(2λ-2,2λ,2λ)=a(-1,0,2)+b(-2,2,1),
所以
所以,
所以DM=DB1,故B正确;
对于C,设F(0,2,t),0≤t≤2,则=(-2,0,t),
易得=(2,2,2),
若异面直线DB1与BF所成的角为45°,
则|cos<,
化简,得t2+8t+4=0,解得t=-4+2或t=-4-2,
又0≤t≤2,所以方程无解,
故点F不存在,故C错误;
对于D,由选项C的分析知,=(-2,2,t),0≤t≤2,易得=(-1,0,2),
所以,
若存在点F,使得点F到直线AE的距离为,
则,化简,得5t2-40t+36=0,
解得t=4+或t=4-,
又0≤t≤2,所以t=4-,故点F存在,故D正确.
故选ABD.
4.解析 (1)证明:若选条件①,连接BD,作PA'⊥平面ABCD,垂足为A'.
∵BP,DP与平面ABCD所成的角相等,∴A'B=A'D,
∴A'在BD的中垂线AC上,
∵在平面PACQ内,PA'⊥AC,PA⊥AC,
∴A'和A重合,∴PA⊥平面ABCD,
又PA 平面PACQ,∴平面PACQ⊥平面ABCD.
若选条件②,设P到平面ABD的距离为h,
∵VP-ABD=S△ABD·h=·h=,∴h=1,
又PA=1,∴PA的长即为点P到平面ABD的距离,即PA⊥平面ABCD,
又PA 平面PACQ,∴平面PACQ⊥平面ABCD.
若选条件③,在△PAB中,由余弦定理得,cos∠BPA=,
∴PB=,∴PB2=PA2+AB2,
∴PA⊥AB,
又PA⊥AC,AC∩AB=A,AC,AB 平面ABCD,
∴PA⊥平面ABCD,
又PA 平面PACQ,∴平面PACQ⊥平面ABCD.
(2)记AC∩BD=O,则OB⊥OC,∵PA⊥平面ABCD,OB,OC 平面ABCD,
∴PA⊥OB,PA⊥OC,取PQ的中点G,连接OG,则OG∥PA,
∴OG⊥OB,OG⊥OC,故OG,OB,OC互相垂直,
以O为坐标原点建立如图所示的空间直角坐标系,
则B(,0,0),Q(0,1,1),
∴,-1,1),
设平面BPQ的一个法向量为m=(x,y,z),
则
令x=,则m=(,0,3),
设平面DPQ的一个法向量为n=(x1,y1,z1),
则
令x1=,则n=(,0,-3),
∴cos=,
又∵∈[0,π],∴=,
由图可知,二面角B-PQ-D是钝二面角,
∴二面角B-PQ-D的大小为.
(3)由(2)知,平面BPQ的一个法向量为m=(,0,3),易知=(0,0,1),
∴点C到平面BPQ的距离d=.
5.解析 (1)证明:∵AB=AD,O为BD的中点,
∴OA⊥BD.
又∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,OA 平面ABD,
∴OA⊥平面BCD,
又∵CD 平面BCD,
∴OA⊥CD.
(2)由题意得OB=OD=OC,
∴△BCD是直角三角形,∠BCD=90°,又BD=2OD=2,CD=1,∴BC=,
由(1)可得,AO是三棱锥A-BCD底面BCD上的高,
∴VA-BCD=×AO×S△BCD=,
∴AO=1,
分别取CB,CD的中点F,G,连接OF,OG,
∵O为BD的中点,∴OF,OG是△BCD的中位线,∴OF∥CD,OG∥BC,又CD⊥BC,∴OF⊥OG,
以O为坐标原点,OF,OG,OA所在直线分别为x轴,y轴,z轴建立空间直角坐标系,如图,
则O(0,0,0),A(0,0,1),B,C,0,D,
∴,
设平面ABC的一个法向量是n1=(x1,y1,z1),
则
则y1=0,令z1=1,得x1=2,则n1=(2,0,1),
故|n1|=,易得||=1,
∴cos∴直线CD和平面ABC所成角的正弦值为.
(3)假设在棱AD上存在点E,使得二面角E-BC-D的大小为45°,
设(0≤λ≤1),
由(2)知,,
易得,
∴,
∴-,-1=,
易知=(0,0,1)是平面BCD的一个法向量,
设平面BCE的一个法向量是n2=(x2,y2,z2),则
即
则y2=0,令x2=2(λ-1),得z2=-λ-1,则n2=(2λ-2,0,-λ-1),
∵二面角E-BC-D的大小为45°,
∴|cos整理得,3λ2-10λ+3=0,解得λ=或λ=3(舍去),
∴,即AE=AD,
∴在棱AD上存在点E,使得二面角E-BC-D的大小为45°,且.
6.解析 (1)由题意知,OP2,OQ3,OP1互相垂直,且OP2=OQ3=OP1=1.
以O为坐标原点,的方向分别为x轴,y轴,z轴的正方向,建立如图所示的空间直角坐标系,
则O(0,0,0),P2(1,0,0),Q3(0,1,0),P1(0,0,1),B2(1,1,0),A1(1,0,1),A2(1,-1,0),Q1(0,0,-1).
所以=(1,1,1),
则cos<,
故异面直线P1A2与Q1B2所成角的余弦值为.
(2)因为E1,E2分别是P1A2,P1B2的中点,
所以E1,
易得.
设平面P1A1E1的一个法向量是n1=(x1,y1,z1),
则
则x1=0,令y1=1,则z1=-1,
所以n1=(0,1,-1),
设平面A1E2P2的一个法向量是n2=(x2,y2,z2),
则
则z2=0,令x2=1,则y2=1,
所以n2=(1,1,0),
则cos=,
所以平面P1A1E1与平面A1E2P2所成的锐二面角的正弦值为.
(3)易得,由(2)知=(-1,0,0),
所以,
所以P2E2∥P1E1,且P2E2=P1E1,
所以四边形P1E1P2E2为平行四边形.
易得=0,
所以,
即P1P2⊥E1E2,
所以四边形P1E1P2E2为菱形,
易得||=1,
所以.
设平面P1E1P2E2的一个法向量是n3=(x3,y3,z3),
则
即
令x3=1,则y3=0,z3=1,
所以n3=(1,0,1).
又=(-1,0,0),所以点A1到平面P1E1P2E2的距离d=,
所以四棱锥A1-P1E1P2E2的体积V1=.
因为,
所以,
所以点A1到直线P1E2的距离h1=.
同理可得,点A1到直线P1E1的距离h2=.
所以四棱锥A1-P1E1P2E2的侧面积S1=.
所以埃舍尔多面体的表面积为12S1=12,体积为12V1=2.
素养点评 本题以“埃舍尔多面体”为背景考查异面直线所成的角、平面与平面所成的锐二面角、几何体的表面积与体积等知识,通过建立空间直角坐标系,实现了点与向量的“坐标化”,将复杂的空间几何体中的位置关系转化为代数运算.本题考查了直观想象、数学建模以及数学运算等核心素养.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025苏教版高中数学选择性必修第二册
综合拔高练
五年高考练
考点1 用空间向量判定、证明平行与垂直
1.(2022全国乙理,7)在正方体ABCD-A1B1C1D1中,E,F分别为AB,BC的中点,则( )
A.平面B1EF⊥平面BDD1
B.平面B1EF⊥平面A1BD
C.平面B1EF∥平面A1AC
D.平面B1EF∥平面A1C1D
2.(2023全国乙理,19)如图,在三棱锥P-ABC中,AB⊥BC,AB=2,BC=2,BP,AP,BC的中点分别为D,E,O,AD=DO,点F在AC上,BF⊥AO.
(1)证明:EF∥平面ADO;
(2)证明:平面ADO⊥平面BEF;
(3)求二面角D-AO-C的正弦值.
考点2 用空间向量求解空间角问题
3.(2022全国甲理,18)在四棱锥P-ABCD中,PD⊥底面ABCD,CD∥AB,AD=DC=CB=1,AB=2,DP=.
(1)证明:BD⊥PA;
(2)求PD与平面PAB所成的角的正弦值.
4.(2024新课标Ⅰ,17)如图,四棱锥P-ABCD中,PA⊥底面ABCD,PA=AC=2,BC=1,AB=.
(1)若AD⊥PB,证明:AD∥平面PBC;
(2)若AD⊥DC,且二面角A-CP-D的正弦值为,求AD.
5.(2024新课标Ⅱ,17)如图,平面四边形ABCD中,AB=8,CD=3,AD=5,∠ADC=90°,∠BAD=30°,点E,F满足.将△AEF沿EF翻折至△PEF,使得PC=4.
(1)证明:EF⊥PD;
(2)求面PCD与面PBF所成的二面角的正弦值.
考点3 用空间向量求解空间距离
6.(2023全国甲理,18)如图,在三棱柱ABC-A1B1C1中,A1C⊥平面ABC,∠ACB=90°,AA1=2,A1到平面BCC1B1的距离为1.
(1)证明:A1C=AC;
(2)已知AA1与BB1的距离为2,求AB1与平面BCC1B1所成角的正弦值.
7.(2024天津,17)已知四棱柱ABCD-A1B1C1D1中,底面ABCD为梯形,AB∥CD,A1A⊥平面ABCD,AD⊥AB,其中AB=AA1=2,AD=DC=1.N是B1C1的中点,M是DD1的中点.
(1)求证:D1N∥平面CB1M;
(2)求平面CB1M与平面BB1C1C的夹角余弦值;
(3)求点B到平面CB1M的距离.
考点4 用空间向量解决立体几何中的最值问题
8.(2021全国甲理,19)已知直三棱柱ABC-A1B1C1中,侧面AA1B1B为正方形,AB=BC=2,E,F分别为AC和CC1的中点,D为棱A1B1上的点,BF⊥A1B1.
(1)证明:BF⊥DE;
(2)当B1D为何值时,面BB1C1C与面DFE所成的二面角的正弦值最小
9.(2020新高考Ⅰ,20)如图,四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD.设平面PAD与平面PBC的交线为l.
(1)证明:l⊥平面PDC;
(2)已知PD=AD=1,Q为l上的点,求PB与平面QCD所成角的正弦值的最大值.
三年模拟练
应用实践
1.(多选题)(2024浙江名校联盟模拟)在正方体ABCD-A1B1C1D1中,AA1=2,点E,F满足,则下列结论正确的有( )
A.直线BE与D1F一定为异面直线
B.直线AE与平面ACB1所成角的正弦值为
C.四面体ADEF的体积恒为2
D.当λ=μ时,AF+A1F的最小值为
2.(多选题)(2023江苏盐城中学三模)已知正方体ABCD-A1B1C1D1的棱长为1,H为棱AA1(包含端点)上的动点,下列命题正确的是( )
A.CH⊥BD
B.二面角D1-AB1-C的平面角的大小为
C.点H到平面CB1D1的距离的取值范围是
D.若CH⊥平面β,则直线CD与平面β所成角的正弦值的取值范围为
3.(多选题)(2023江苏扬州期末)如图,正方体ABCD-A1B1C1D1的棱长为2,E为线段A1D1的中点,F为线段CC1上的一个动点,则下列说法正确的是( )
A.当F为CC1的中点时,点B1到平面AEF的距离为
B.当F为CC1的中点时,记DB1与平面AEF的交点为M,则DM=DB1
C.存在点F,使得异面直线DB1与BF所成的角为45°
D.存在点F,使得点F到直线AE的距离为
4.(2023江苏镇江中学三模)如图,四边形ABCD是边长为2的菱形,∠ABC=60°,四边形PACQ为矩形,PA=1,从下列三个条件中任选一个作为已知条件,并解答问题.
①BP,DP与平面ABCD所成的角相等;②三棱锥P-ABD的体积为;③cos∠BPA=.
(1)证明:平面PACQ⊥平面ABCD;
(2)求二面角B-PQ-D的大小;
(3)求点C到平面BPQ的距离.
5.(2024江苏镇江中学检测)如图,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,O为BD的中点,△OCD是边长为1的等边三角形,且VA-BCD=.
(1)证明:OA⊥CD;
(2)求直线CD与平面ABC所成角的正弦值;
(3)在棱AD上是否存在点E,使得二面角E-BC-D的大小为45° 若存在,求出的值;若不存在,请说明理由.
迁移创新
6.(2023上海南洋模范中学期末)《瀑布》(图1)是为人所熟知的作品之一,图中的瀑布会源源不断地落下,落下的水又逆流而上,荒唐至极,但又会让你百看不腻,画面下方还有一位饶有兴致的观察者,似乎她没发现什么不对劲.画面两座高塔上各有一个几何体,左塔上方是著名的“三立方体合体”,它由三个正方体构成,右塔上的几何体是首次出现,后称“埃舍尔多面体”.
图1
埃舍尔多面体可以用两两垂直且中心重合的三个正方形构造,设边长均为2,定义正方形AnBnCnDn,n=1,2,3的顶点为“框架点”,定义两正方形交线为“极轴”,其端点为“极点”,记为Pn,Qn,将极点P1,Q1分别与正方形A2B2C2D2的顶点连线,取其中点记为Em,Fm,m=1,2,3,4(如图2).埃舍尔多面体可视部分是由12个四棱锥构成的,这些四棱锥顶点均为“框架点”,底面四边形由两个“极点”与两个“中点”构成,为了便于理解,图3中我们构造了其中两个四棱锥A1-P1E1P2E2和A2-P2E1P3F1.
(1)求异面直线P1A2与Q1B2所成角的余弦值;
(2)求平面P1A1E1与平面A1E2P2所成的锐二面角的正弦值;
(3)求埃舍尔多面体的表面积与体积(直接写出答案).
图2
图3
答案与分层梯度式解析
综合拔高练
五年高考练
1.A 如图,以D为坐标原点,建立空间直角坐标系D-xyz,设AB=2,
则B1(2,2,2),E(2,1,0),D(0,0,0),F(1,2,0),B(2,2,0),A1(2,0,2),A(2,0,0),C(0,2,0),C1(0,2,2),
所以=(-2,2,0),
设平面B1EF的一个法向量为m=(x,y,z),
则
令x=2,则y=2,z=-1,
所以m=(2,2,-1),
因为平面BDD1的一个法向量为=(-2,2,0),
且·m=-2×2+2×2+(-1)×0=0,
所以⊥m,所以平面B1EF⊥平面BDD1,故A正确;
同理可得,平面A1BD的一个法向量为n1=(1,-1,-1),平面A1AC的一个法向量为n2=(1,1,0),平面A1C1D的一个法向量为n3=(1,1,-1),
因为m·n1=2-2+1=1≠0,所以平面B1EF与平面A1BD不垂直,故B错误;
因为m与n2不平行,所以平面B1EF与平面A1AC不平行,
故C错误;
因为m与n3不平行,所以平面B1EF与平面A1C1D不平行,故D错误.
故选A.
高考风向 空间直线、平面的位置关系是高考的高频考点,证明平行与垂直的常用方法是几何法和坐标法,利用几何法解题的关键是熟练掌握三种平行关系、三种垂直关系的转化和作出恰当的辅助线;利用坐标法解题的关键是直线的方向向量、平面的法向量间的位置关系,即向量运算.要注意结合图形灵活选择恰当的方法,利用坐标法证明或求解时,要避免运算错误.本题以正方体为载体,证明面面平行、面面垂直,体现了试题的基础性和综合性.
2.解析 以BA,BC所在直线分别为x轴,y轴,垂直于平面ABC的直线为z轴,建立如图2所示的空间直角坐标系,
则B(0,0,0),A(2,0,0),O(0,,0).
(1)证明:设AF=λAC,0<λ<1.
由得F(2-2λ,2λ,0),
∴λ,0),
又,0),BF⊥AO,
∴=0,即-2(2-2λ)+4λ=0,解得λ=,
故F为AC的中点.
又D,E,O分别为PB,PA,BC的中点,
∴DO∥PC,EF∥PC,
∴DO∥EF,
又EF 平面ADO,DO 平面ADO,
∴EF∥平面ADO.
(2)证明:∵D,O分别是PB,BC的中点,且PC=,
∴DO=,又AD=.
由cos∠ABD=,得PA=.
设P(x,y,z),z>0,则由PB=PC=(z>0),
解得故P(-1,),
又∵D,E分别是PB,PA的中点,
∴D,
∴,
又,0),
∴=0,
∴,即AO⊥BE,
又AO⊥BF,BE∩BF=B,BE、BF 平面BEF,
∴AO⊥平面BEF,又AO 平面ADO,
∴平面ADO⊥平面BEF.
(3)易知平面AOC的一个法向量为m1=(0,0,1),
由(2)知,
设平面AOD的一个法向量为m2=(x1,y1,z1),则
即
取x1=1,则y1=,
则m2=(1,),
设二面角D-AO-C的平面角的大小为θ,则|cos θ|=
|cos
∴sin θ=,
即二面角D-AO-C的正弦值为.
3.解析 以D为原点,DC,DP所在直线分别为y轴,z轴,过D点且垂直于AB的直线为x轴,建立空间直角坐标系,如图.
(1)证明:结合题意知D(0,0,0),B,
则,
∴+0=0,
∴,∴BD⊥PA.
(2)设平面PAB的一个法向量为m=(x,y,z),
由(1)知=(0,2,0),
∴
则y=0,令z=1,则x=2,故m=(2,0,1).
又∵),
∴PD与平面PAB所成的角的正弦值等于|cos<,m>|=.
高考风向 求直线与平面所成的角是高考中常见的一种问题.线面角求解的常用方法是坐标法和几何法.利用坐标法解题的关键是求出平面法向量及直线的方向向量的坐标,本题的条件中含有线面垂直,有利于建立空间直角坐标系,进而通过坐标法求线面角的正弦值.利用坐标法求线面角,本质是把几何关系转化为向量运算.利用坐标法解决问题时,要防止运算错误.
4.解析 (1)证明:在△ABC中,AB=,BC=1,AC=2,
故有AB2+BC2=AC2,所以AB⊥BC.
因为PA⊥底面ABCD,AD 平面ABCD,
所以PA⊥AD,
又因为AD⊥PB,PB∩PA=P,PB,PA 平面PAB,
所以AD⊥平面PAB,又AB 平面PAB,
所以AD⊥AB,
又因为AB⊥BC,A,B,C,D在同一平面内,
所以AD∥BC.
又因为BC 平面PBC,AD 平面PBC,
所以AD∥平面PBC.
(2)因为AD⊥DC,所以以DA,DC所在直线分别为x轴,y轴,过D作与PA平行的直线为z轴,建立空间直角坐标系,如图,
则D(0,0,0),
设AD=m(m>0),则DC=,0).
,0),
设平面ACP的一个法向量为n1=(x1,y1,z1),
则
即不妨取x1=,
则n1=(,m,0).
设平面DCP的一个法向量为n2=(x2,y2,z2),
则
易知y2=0,不妨取z2=m,
则x2=-2,故n2=(-2,0,m).
因为二面角A-CP-D的正弦值为,
所以|cos
解得m=(舍负),
所以AD=.
5.解析 (1)证明:由题知AE=AB=4,∠FAE=30°,
∴EF==2,
∴EF2+AE2=AF2,∴AE⊥EF,
∴EF⊥PE,又PE∩AE=E,PE,AE 平面PED,∴EF⊥平面PED,又PD 平面PED,∴EF⊥PD.
(2)连接EC,∵CD=3,DE=AD-AE=3,∠ADC=90°,∴EC==6,
又PE=AE=2,∴EC2+PE2=PC2,∴PE⊥EC,又PE⊥EF,EC∩EF=E,EC,EF 平面ABCD,
∴PE⊥平面ABCD,
又ED 平面ABCD,∴PE⊥ED,又PE⊥EF,EF⊥ED,
∴PE,EF,ED两两垂直,
∴以E为原点,EF,ED,EP所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,如图,
则A(0,-2),
∴,0),
=(3,0,0).
设m=(x1,y1,z1),n=(x2,y2,z2)分别为平面PBF,平面PCD的一个法向量,
∴
令x1=,则m=(,-1,1),令y2=2,则n=(0,2,3).
∴cos
∴sin
∴所求正弦值为.
6.解析 (1)证明:∵A1C⊥平面ABC,BC 平面ABC,∴A1C⊥BC.
∵∠ACB=90°,∴AC⊥BC.
又AC∩A1C=C,AC,A1C 平面AA1C1C,
∴BC⊥平面AA1C1C.
又∵BC 平面BCC1B1,
∴平面BCC1B1⊥平面AA1C1C.
过A1作A1H⊥CC1,垂足为H,又平面BCC1B1⊥平面AA1C1C,平面BCC1B1∩平面AA1C1C=CC1,A1H 平面AA1C1C,
∴A1H⊥平面BCC1B1,
∴A1H=1.
易知∠CA1C1=90°,在Rt△A1CC1中,CC1=2=2A1H,
∴H为CC1的中点,
∴△A1CC1为等腰直角三角形,
∴A1C=A1C1.
易知AC A1C1,∴A1C=AC.
(2)以C为坐标原点,CA,CB,CA1所在直线分别为x轴,y轴,z轴建立空间直角坐标系.在平面BCC1B1内,过H作HQ∥BC,交BB1于点Q,连接A1Q,如图.
易知CC1⊥A1H,CC1⊥HQ,CC1 BB1,又A1H∩HQ=H,A1H,HQ 平面A1HQ,∴CC1⊥平面A1HQ,BB1⊥平面A1HQ,又A1Q 平面A1HQ,∴BB1⊥A1Q,∴A1Q=2,∴在Rt△A1HQ中,HQ=.
易知A1C=AC=,则A().
设平面BCC1B1的一个法向量为n=(x,y,z),
则取x=1,得n=(1,0,1).
设直线AB1与平面BCC1B1所成的角为θ,
则sin θ=|cos<,n>|==
.
∴AB1与平面BCC1B1所成角的正弦值为.
7.解析 (1)证明:取B1C的中点P,连接NP,MP,
又N为B1C1的中点,
所以在△B1CC1中,NP∥CC1,NP=CC1,
因为M是DD1的中点,DD1∥CC1,
所以D1M=CC1,且D1M∥CC1,
则有D1M∥NP,D1M=NP,故四边形D1MPN是平行四边形,
所以D1N∥MP,又MP 平面CB1M,D1N 平面CB1M,
所以D1N∥平面CB1M.
(2)已知A1A⊥平面ABCD,AD⊥AB,所以以A为原点,建立如图所示的空间直角坐标系,
易知AB=AA1=2,AD=DC=1,
则B(2,0,0),C(1,1,0),B1(2,0,2),M(0,1,1),
所以=(0,0,2).
设平面CB1M与平面BB1C1C的一个法向量分别为m=(x1,y1,z1),n=(x2,y2,z2).
则
则z2=0.分别取x1=1,x2=1,得y1=3,z1=1,y2=1,
所以m=(1,3,1),n=(1,1,0),
则|cos
故平面CB1M与平面BB1C1C夹角的余弦值为.
(3)由(2)知=(0,0,2),平面CB1M的一个法向量为m=(1,3,1),
则,
即点B到平面CB1M的距离为.
8.解析 ∵BF⊥A1B1,B1B⊥A1B1,BF∩B1B=B,BF 平面B1C1CB,BB1 平面B1C1CB,∴A1B1⊥平面B1C1CB.
∵AB∥A1B1,∴AB⊥平面B1C1CB,
又∵BC 平面B1C1CB,∴AB⊥BC.
以B为坐标原点,BA,BC,BB1所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系,
则B(0,0,0),F(0,2,1),E(1,1,0),
∴=(0,2,1),设B1D=a(0≤a≤2),则D(a,0,2),
∴=(1-a,1,-2).
(1)证明:∵=(0,2,1)·(1-a,1,-2)=0×(1-a)+2×1+1×(-2)=0,
∴BF⊥DE.
(2)=(a,-2,1),
设平面DFE的一个法向量为n=(x,y,z),
则
不妨设x=1,则y=,
∴n=.
易知m=(1,0,0)是平面BB1C1C的一个法向量.
设平面BB1C1C与平面DEF所成的锐二面角的大小为θ,
则cos θ=|cos
=
=,∴sin θ=,
故当a=,即B1D=时,平面BB1C1C与平面DFE所成的二面角的正弦值最小,最小值为.
解题反思 (1)证明线线垂直常用的方法是先证明线面垂直,也可以通过计算两直线的方向向量的数量积为0证明,即“以算代证”.
(2)求解最大值、最小值以及取值范围问题时,通常建立目标函数,通过求函数的最值或值域解决,本题建立空间直角坐标系,在题中设出B1D=a(0≤a≤2),得D(a,0,2),通过平面与平面所成的锐二面角的余弦值最大,求得正弦值最小是关键一步.
9.解析 (1)证明:因为PD⊥底面ABCD,所以PD⊥AD.因为底面ABCD为正方形,所以AD⊥DC.又DC∩PD=D,DC,PD 平面PDC,所以AD⊥平面PDC.
因为AD∥BC,AD 平面PBC,所以AD∥平面PBC.
由已知得l∥AD,
因此l⊥平面PDC.
(2)以D为坐标原点,的方向分别为x轴,y轴,z轴的正方向,建立空间直角坐标系D-xyz(图略),则D(0,0,0),C(0,1,0),B(1,1,0),P(0,0,1),
所以=(1,1,-1).
由(1)可设Q(a,0,1),则=(a,0,1).
设平面QCD的一个法向量是n=(x,y,z),
则
取x=-1,
则n=(-1,0,a).
所以cos
则sin θ=.
因为,当且仅当a=1时等号成立,所以PB与平面QCD所成角的正弦值的最大值为.
三年模拟练
1.ABD 2.ACD 3.ABD
1.ABD 以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,如图1,
则A(2,0,0),B(2,2,0),C(0,2,0),D(0,0,0),A1(2,0,2),B1(2,2,2),E(0,0,1),
所以=(-2,0,0).
由(0<λ<1,0<μ<1)得=(-2μ,2,2λ),所以F(2-2μ,2,2λ).
由于0<λ<1,0<μ<1,所以0<2-2μ<2,0<2λ<2,所以点F在平面BCC1B1内(不包括边界),连接BD,B1D1,又D1在平面BB1D1D内,所以D1F和平面BB1D1D相交,
又BE 平面BB1D1D,D1 直线BE,所以直线BE与D1F一定为异面直线,故A正确.
易得=(-2,0,1).
设平面ACB1的一个法向量为m=(x,y,z),
则
令y=1,得x=1,z=-1,则m=(1,1,-1),
所以cos<,m>=,
设直线AE与平面ACB1所成的角为θ,θ∈,
则sin θ=|cos<,m>|=,故B正确.
因为点F在平面BCC1B1内(不包括边界),所以点F到平面ADE的距离为2,所以V四面体ADEF=,故C错误.
当λ=μ时,F(2-2λ,2,2λ),连接BC1,则点F在BC1上(不含端点).
连接A1B,A1C1,将平面A1BC1绕BC1翻折到与平面ABC1D1在同一平面内,如图2,
连接AA1,此时AA1与BC1的交点即为当λ=μ时,使AF+A1F取最小值的点F.
由题意可知AB=2,A1B=2,∠ABA1=,
所以A=AB2+A1B2-2AB·A1Bcos∠ABA1=22+(2×cos ,
所以AA1=,
所以AF+A1F的最小值为,故D正确.
故选ABD.
2.ACD 以D为坐标原点建立如图所示的空间直角坐标系,
则D(0,0,0),B(1,1,0),C(0,1,0),A(1,0,0),D1(0,0,1),C1(0,1,1),B1(1,1,1),
设H(1,0,h),0≤h≤1.
对于A,=(1,1,0),则=0,即CH⊥BD,故A正确.
对于B,=(-1,1,0),
设平面AB1D1的一个法向量为m=(x,y,z),
则
令z=1,得x=1,y=-1,则m=(1,-1,1).
设平面AB1C的一个法向量为n=(a,b,c),
则
令b=1,得a=1,c=-1,则n=(1,1,-1).
故cos
由图可知,二面角D1-AB1-C为锐二面角,故其余弦值为,故二面角D1-AB1-C的平面角的大小不是,故B错误.
对于C,=(0,1,-1),
设平面CB1D1的一个法向量为k=(p,q,r),
则
令q=1,得p=-1,r=1,则k=(-1,1,1).
又=(0,-1,h-1),
∴点H到平面CB1D1的距离为||·,故C正确.
对于D,设直线CD与平面β所成的角为θ.
∵CH⊥平面β,∴=(1,-1,h)为平面β的一个法向量,
又=(0,1,0),∴sin θ=|cos<,
又h∈[0,1],∴,故D正确.
故选ACD.
方法总结 对于空间中位置关系的判断、角的计算或取值范围的求解问题,可结合几何体的结构特征建立合适的空间直角坐标系,通过向量的共线、向量的数量积等来判断位置关系,通过平面的法向量、直线的方向向量等来处理相关角的计算或取值范围的求解问题.
3.ABD 如图,以D为坐标原点建立空间直角坐标系,
则D(0,0,0),A(2,0,0),E(1,0,2),B1(2,2,2),B(2,2,0),
当F为CC1的中点时,F(0,2,1),
对于A,易得=(-2,2,1),
设平面AEF的一个法向量为m=(x,y,z),则
令z=1,得x=2,y=,则m=,
又=(0,2,2),
所以点B1到平面AEF的距离为,故A正确;
对于B,设(0≤λ≤1),则M(2λ,2λ,2λ),
又点M在平面AEF内,则,即(2λ-2,2λ,2λ)=a(-1,0,2)+b(-2,2,1),
所以
所以,
所以DM=DB1,故B正确;
对于C,设F(0,2,t),0≤t≤2,则=(-2,0,t),
易得=(2,2,2),
若异面直线DB1与BF所成的角为45°,
则|cos<,
化简,得t2+8t+4=0,解得t=-4+2或t=-4-2,
又0≤t≤2,所以方程无解,
故点F不存在,故C错误;
对于D,由选项C的分析知,=(-2,2,t),0≤t≤2,易得=(-1,0,2),
所以,
若存在点F,使得点F到直线AE的距离为,
则,化简,得5t2-40t+36=0,
解得t=4+或t=4-,
又0≤t≤2,所以t=4-,故点F存在,故D正确.
故选ABD.
4.解析 (1)证明:若选条件①,连接BD,作PA'⊥平面ABCD,垂足为A'.
∵BP,DP与平面ABCD所成的角相等,∴A'B=A'D,
∴A'在BD的中垂线AC上,
∵在平面PACQ内,PA'⊥AC,PA⊥AC,
∴A'和A重合,∴PA⊥平面ABCD,
又PA 平面PACQ,∴平面PACQ⊥平面ABCD.
若选条件②,设P到平面ABD的距离为h,
∵VP-ABD=S△ABD·h=·h=,∴h=1,
又PA=1,∴PA的长即为点P到平面ABD的距离,即PA⊥平面ABCD,
又PA 平面PACQ,∴平面PACQ⊥平面ABCD.
若选条件③,在△PAB中,由余弦定理得,cos∠BPA=,
∴PB=,∴PB2=PA2+AB2,
∴PA⊥AB,
又PA⊥AC,AC∩AB=A,AC,AB 平面ABCD,
∴PA⊥平面ABCD,
又PA 平面PACQ,∴平面PACQ⊥平面ABCD.
(2)记AC∩BD=O,则OB⊥OC,∵PA⊥平面ABCD,OB,OC 平面ABCD,
∴PA⊥OB,PA⊥OC,取PQ的中点G,连接OG,则OG∥PA,
∴OG⊥OB,OG⊥OC,故OG,OB,OC互相垂直,
以O为坐标原点建立如图所示的空间直角坐标系,
则B(,0,0),Q(0,1,1),
∴,-1,1),
设平面BPQ的一个法向量为m=(x,y,z),
则
令x=,则m=(,0,3),
设平面DPQ的一个法向量为n=(x1,y1,z1),
则
令x1=,则n=(,0,-3),
∴cos
又∵
由图可知,二面角B-PQ-D是钝二面角,
∴二面角B-PQ-D的大小为.
(3)由(2)知,平面BPQ的一个法向量为m=(,0,3),易知=(0,0,1),
∴点C到平面BPQ的距离d=.
5.解析 (1)证明:∵AB=AD,O为BD的中点,
∴OA⊥BD.
又∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,OA 平面ABD,
∴OA⊥平面BCD,
又∵CD 平面BCD,
∴OA⊥CD.
(2)由题意得OB=OD=OC,
∴△BCD是直角三角形,∠BCD=90°,又BD=2OD=2,CD=1,∴BC=,
由(1)可得,AO是三棱锥A-BCD底面BCD上的高,
∴VA-BCD=×AO×S△BCD=,
∴AO=1,
分别取CB,CD的中点F,G,连接OF,OG,
∵O为BD的中点,∴OF,OG是△BCD的中位线,∴OF∥CD,OG∥BC,又CD⊥BC,∴OF⊥OG,
以O为坐标原点,OF,OG,OA所在直线分别为x轴,y轴,z轴建立空间直角坐标系,如图,
则O(0,0,0),A(0,0,1),B,C,0,D,
∴,
设平面ABC的一个法向量是n1=(x1,y1,z1),
则
则y1=0,令z1=1,得x1=2,则n1=(2,0,1),
故|n1|=,易得||=1,
∴cos
(3)假设在棱AD上存在点E,使得二面角E-BC-D的大小为45°,
设(0≤λ≤1),
由(2)知,,
易得,
∴,
∴-,-1=,
易知=(0,0,1)是平面BCD的一个法向量,
设平面BCE的一个法向量是n2=(x2,y2,z2),则
即
则y2=0,令x2=2(λ-1),得z2=-λ-1,则n2=(2λ-2,0,-λ-1),
∵二面角E-BC-D的大小为45°,
∴|cos
∴,即AE=AD,
∴在棱AD上存在点E,使得二面角E-BC-D的大小为45°,且.
6.解析 (1)由题意知,OP2,OQ3,OP1互相垂直,且OP2=OQ3=OP1=1.
以O为坐标原点,的方向分别为x轴,y轴,z轴的正方向,建立如图所示的空间直角坐标系,
则O(0,0,0),P2(1,0,0),Q3(0,1,0),P1(0,0,1),B2(1,1,0),A1(1,0,1),A2(1,-1,0),Q1(0,0,-1).
所以=(1,1,1),
则cos<,
故异面直线P1A2与Q1B2所成角的余弦值为.
(2)因为E1,E2分别是P1A2,P1B2的中点,
所以E1,
易得.
设平面P1A1E1的一个法向量是n1=(x1,y1,z1),
则
则x1=0,令y1=1,则z1=-1,
所以n1=(0,1,-1),
设平面A1E2P2的一个法向量是n2=(x2,y2,z2),
则
则z2=0,令x2=1,则y2=1,
所以n2=(1,1,0),
则cos
所以平面P1A1E1与平面A1E2P2所成的锐二面角的正弦值为.
(3)易得,由(2)知=(-1,0,0),
所以,
所以P2E2∥P1E1,且P2E2=P1E1,
所以四边形P1E1P2E2为平行四边形.
易得=0,
所以,
即P1P2⊥E1E2,
所以四边形P1E1P2E2为菱形,
易得||=1,
所以.
设平面P1E1P2E2的一个法向量是n3=(x3,y3,z3),
则
即
令x3=1,则y3=0,z3=1,
所以n3=(1,0,1).
又=(-1,0,0),所以点A1到平面P1E1P2E2的距离d=,
所以四棱锥A1-P1E1P2E2的体积V1=.
因为,
所以,
所以点A1到直线P1E2的距离h1=.
同理可得,点A1到直线P1E1的距离h2=.
所以四棱锥A1-P1E1P2E2的侧面积S1=.
所以埃舍尔多面体的表面积为12S1=12,体积为12V1=2.
素养点评 本题以“埃舍尔多面体”为背景考查异面直线所成的角、平面与平面所成的锐二面角、几何体的表面积与体积等知识,通过建立空间直角坐标系,实现了点与向量的“坐标化”,将复杂的空间几何体中的位置关系转化为代数运算.本题考查了直观想象、数学建模以及数学运算等核心素养.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
