2025苏教版高中数学选择性必修第二册强化练习题--第9章 统计
文档属性
| 名称 | 2025苏教版高中数学选择性必修第二册强化练习题--第9章 统计 |

|
|
| 格式 | docx | ||
| 文件大小 | 425.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-15 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025苏教版高中数学选择性必修第二册
第9章 统计
全卷满分150分 考试用时120分钟
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.某公司收集了某商品销售收入y(万元)与相应的广告支出x(万元)的10组数据(xi,yi)(i=1,2,3,…,10),绘制出如下散点图,并利用线性回归模型进行拟合.
若去掉A点后再重新进行线性回归分析,则下列说法正确的是( )
A.决定系数R2变小
B.残差平方和变小
C.样本相关系数r的值变小
D.x与y的相关性变弱
2.某班班主任对全班50名学生学习积极性与对待班级工作的态度进行了调查,统计数据如下表所示:
主动参加班级工作 不太主动参加班级工作 合计
学习积极性高 18 7 25
学习积极性一般 6 19 25
合计 24 26 50
则以下说法正确的是( )
附:χ2=,其中n=a+b+c+d.
P(χ2≥x0) 0.05 0.025 0.010 0.005 0.001
x0 3.841 5.024 6.635 7.879 10.828
A.有99.9%的把握认为学生的学习积极性与对待班级工作的态度有关系
B.有99.5%的把握认为学生的学习积极性与对待班级工作的态度没有关系
C.有99%的把握认为学生的学习积极性与对待班级工作的态度没有关系
D.没有充分的证据显示学生的学习积极性与对待班级工作的态度有关系
3.根据最小二乘法求得一组样本数据(xi,yi)(其中i=1,2,…,300)的经验回归方程是,则下列说法正确的是( )
A.至少有一个样本点落在经验回归直线上
B.若所有样本点都在经验回归直线上,则变量间的样本相关系数为1
C.对所有的变量xi(i=1,2,…,300),的值一定与yi有误差
D.若经验回归直线>0,则变量x与y正相关
4.为维护市场秩序,保护消费者权益,在十一假期来临之际,某市物价部门对某商品在5家商场的售价x(元)及其一天的销售量y(件)进行调查,得到五组数据(xi,yi)(i=1,2,3,4,5),经过分析、计算,得=8,y关于x的经验回归方程为,则相应于点(9,10)的残差为( )
A.-1 B.1 C.-3 D.3
5.为促进学生积极参加体育锻炼,养成良好的锻炼习惯,提高体质健康水平,某学校从全校学生中随机抽取200名学生进行“是否喜欢体育锻炼”的问卷调查,统计结果如下表:
性别 体育锻炼 合计
喜欢 不喜欢
男
女 50 80
合计 110
附:χ2=,其中n=a+b+c+d.
P(χ2≥x0) 0.05 0.025 0.010 0.005 0.001
x0 3.841 5.024 6.635 7.879 10.828
下列结论不正确的是( )
A.样本中男生所占比例为60%
B.估计该校不喜欢体育锻炼的学生所占比例为45%
C.样本中喜欢体育锻炼的男生比喜欢体育锻炼的女生多50人
D.没有99.9%的把握认为是否喜欢体育锻炼与性别有关
6.某工厂为了对研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价x/元 9 9.2 9.4 9.6 9.8 10
销量y/件 100 94 93 90 85 78
预计在今后的销售中,销量与单价仍然满足这种线性相关关系,且该产品的成本是5元/件,为使工厂获得最大利润,该产品的单价应定为( )
参考公式:对于一组数据(x1,y1),(x2,y2),…,(xn,yn),其经验回归直线.
参考数据:.
A.9.4元 B.9.5元
C.9.6元 D.9.7元
7.为了解喜爱足球是否与性别有关,随机抽取了若干人进行调查,抽取女性人数是男性人数的2倍,男性喜爱足球的人数占男性人数的,若本次调查得出“至少有99.5%的把握认为喜爱足球与性别有关”的结论,则被调查的男性至少有( )
附:χ2=,其中n=a+b+c+d.
P(χ2≥x0) 0.10 0.05 0.010 0.005 0.001
x0 2.706 3.841 6.635 7.879 10.828
A.11人 B.12人 C.13人 D.14人
8.已知变量y关于变量x的回归方程为=e10.7,则x=( )
x 1 2 3 4
y e e3 e4 e6
A.5 B.6 C.7 D.8
二、多项选择题(本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分)
9.下列说法正确的是( )
A.在回归分析中,残差的平方和越小,模型的拟合效果越好
B.在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适
C.若数据x1,x2,…,xn的平均数为1,则2x1,2x2,…,2xn的平均数为2
D.对分类变量x与y的统计量χ2的观测值x0来说,x0越小,判断“x与y有关系”的把握越大
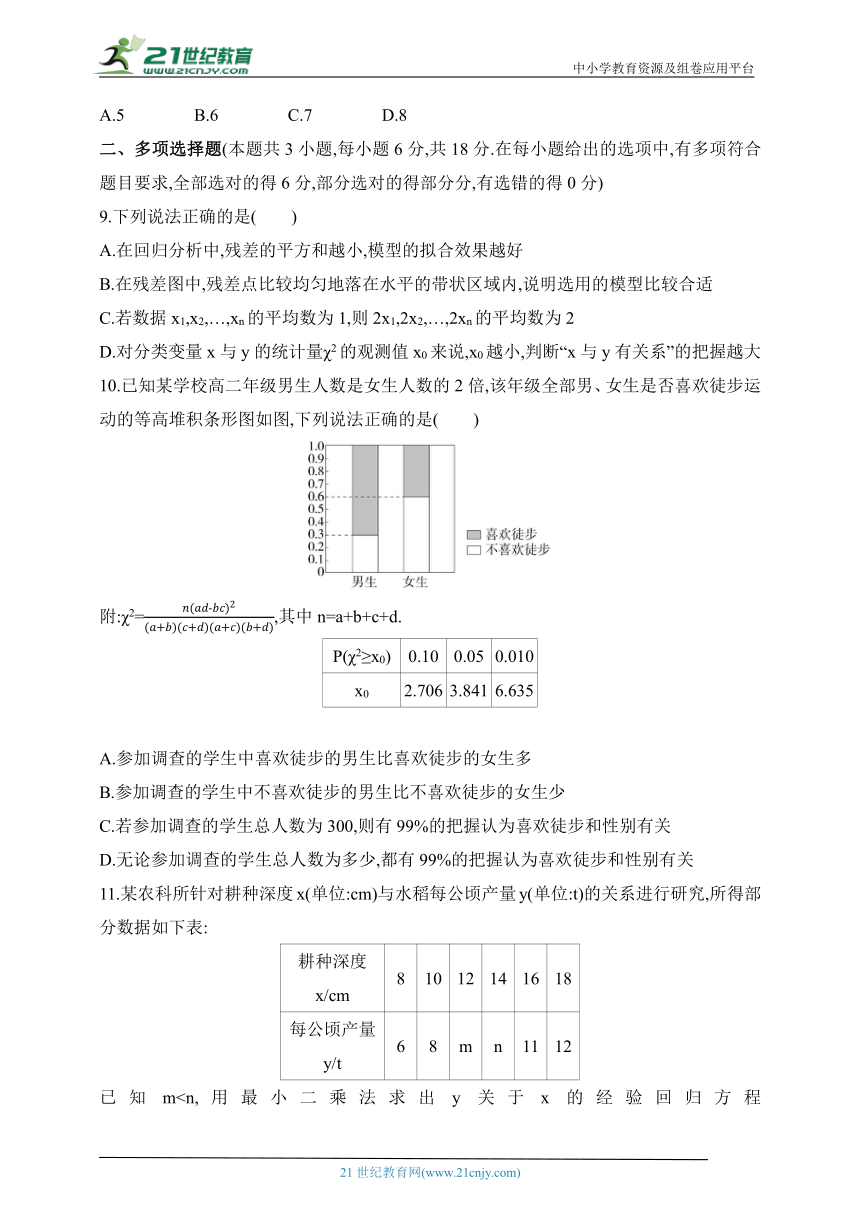
10.已知某学校高二年级男生人数是女生人数的2倍,该年级全部男、女生是否喜欢徒步运动的等高堆积条形图如图,下列说法正确的是( )
附:χ2=,其中n=a+b+c+d.
P(χ2≥x0) 0.10 0.05 0.010
x0 2.706 3.841 6.635
A.参加调查的学生中喜欢徒步的男生比喜欢徒步的女生多
B.参加调查的学生中不喜欢徒步的男生比不喜欢徒步的女生少
C.若参加调查的学生总人数为300,则有99%的把握认为喜欢徒步和性别有关
D.无论参加调查的学生总人数为多少,都有99%的把握认为喜欢徒步和性别有关
11.某农科所针对耕种深度x(单位:cm)与水稻每公顷产量y(单位:t)的关系进行研究,所得部分数据如下表:
耕种深度x/cm 8 10 12 14 16 18
每公顷产量y/t 6 8 m n 11 12
已知m参考数据:两个变量x,y之间的样本相关系数r=.
参考公式:在经验回归方程中,.
A.m+n=17 B.
C. D.ε1+ε2=-1
三、填空题(本题共3小题,每小题5分,共15分)
12.已知一组数据(18,24),(13,34),(10,38),(-1,m)的经验回归方程为=-2x+59.5,则该组数据的样本相关系数r= (精确到0.001).
13.某校数学建模兴趣小组收集了一组恒温动物体重W(单位:克)与其脉搏率f(单位:次/分钟)的对应数据(Wi,fi)(i=1,2,…,8),根据生物学常识和散点图得出f与W近似满足f=cWk(c,k为参数).令xi=lnWi,yi=lnfi,计算得=214.由最小二乘法得经验回归方程为x+7.4,则k的值为 ;为判断拟合效果,通过经验回归方程求得预测值(i=1,2,…,8),若残差平方和)2≈0.28,则决定系数R2= .
参考公式:决定系数R2=1-.
14.新疆某农科所为了研究不同土壤环境下棉花的品质,选取了甲、乙两块试验田进行种植.在棉花成熟后采摘,分别从甲、乙两块试验田采摘的棉花中各随机抽取50份样本,测定其马克隆值,整理测量数据得到如下2×2列联表(单位:份),其中40≤a≤50且a∈N*.
注:棉花的马克隆值是反映棉花纤维细度与成熟度的综合指标,是棉花纤维重要的内在质量指标之一.根据国家标准规定,马克隆值可分为A,B,C三个级别,A级品质最好,B级品质为标准,C级品质最差.
A级或B级 C级 合计
甲试验田 a 50-a 50
乙试验田 80-a a-30 50
合计 80 20 100
当a=a0时,至少有99%的把握认为该品种棉花的马克隆值级别与土壤环境有关,则a0的最小值为 .
附:χ2=,其中n=a+b+c+d.
P(χ2≥x0) 0.05 0.010 0.001
x0 3.841 6.635 10.828
四、解答题(本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤)
15.(13分)甲公司推出一种新产品,为了解某地区消费者对新产品的满意度,从中随机调查了1000名消费者,得到下表:
满意 不满意
男 440 60
女 460 40
(1)能否有95%的把握认为消费者对新产品的满意度与性别有关
(2)若用频率估计概率,从该地区消费者中随机选取3人,用X表示不满意的人数,求X的概率分布与数学期望.
附:χ2=,其中n=a+b+c+d.
P(χ2≥x0) 0.10 0.05 0.010
x0 2.706 3.841 6.635
16.(15分)为了了解高中学生每天课后自主学习数学的时间x(分钟)和他们的数学成绩y(分)的关系,某试验小组做了调查,得到一些数据(表1).
表1
编号 1 2 3 4 5
学习时间x/分钟 30 40 50 60 70
数学成绩y/分 65 78 85 99 108
(1)经分析,可用线性回归模型拟合y与x的关系,请求出经验回归方程,并由此预测每天课后自主学习数学的时间为100分钟时的数学成绩;
(2)根据上述调查,某校提倡学生周末自主学习.经过一学期的实施后,抽样调查了220名学生.按照是否参与周末自主学习以及成绩是否有进步进行统计,得到2×2列联表(表2).依据表中数据,判断是否有99.9%的把握认为“周末自主学习与成绩进步”有关.
表2
成绩没有进步 成绩有进步 合计
参与周末 自主学习 35 130 165
未参与周末 自主学习 25 30 55
合计 60 160 220
附:①yi=435,xi的方差为200;
②在经验回归方程;
③χ2=,其中n=a+b+c+d.
P(χ2≥x0) 0.10 0.05 0.010 0.005 0.001
x0 2.706 3.841 6.635 7.879 10.828
17.(15分)春季流感对人们的健康生活带来了一定的影响,为了有效预防流感,很多人注射了流感疫苗.某市防疫部门从辖区居民中随机抽取了1000人进行调查,发现其中注射疫苗的800人中有220人感染流感,另外没注射疫苗的200人中有80人感染流感.医学研究表明,流感的检测结果是有错检的可能,已知患有流感的人其检测结果有95%的可能呈阳性(感染),而没有患流感的人其检测结果有99%的可能呈阴性(未感染).
(1)估计该市流感感染率是多少;
(2)根据所给数据,判断是否有99.9%的把握认为注射流感疫苗与预防流感有关;
(3)已知某人的流感检测结果呈阳性,求此人真的患有流感的概率.(精确到0.001)
附:χ2=,其中n=a+b+c+d.
P(χ2≥x0) 0.10 0.05 0.010 0.005 0.001
x0 2.706 3.841 6.635 7.879 10.828
18.(17分)某大型企业对其产品进行研发与创新,根据市场调研与模拟,得到研发投入x(亿元)与研发创新的直接收益y(亿元)的数据统计如下:
x 2 3 4 6 8 10 13 21 22 23 24 25
y 13 22 31 42 50 56 58 68.5 68 67.5 66 66
当0(1)根据下列表格中的数据,比较当0回归模型 模型① 模型②
回归方程 =4.1x+11.8 -14.4
)2 182.4 79.2
(2)为鼓励科技创新,当研发的投入不少于20亿元时,国家给予公司补贴收益10亿元,以经验回归方程为预测依据,比较研发投入17亿元与20亿元时公司实际收益的大小;
(3)研发改造后,该公司F产品的效率X大幅提高,X服从正态分布N(0.52,0.012),公司对研发团队的奖励方案如下:若F产品的效率不超过50%,不予奖励;若F产品的效率超过50%但不超过53%,每件F产品奖励2万元;若F产品的效率超过53%,每件F产品奖励5万元.求每件F产品获得奖励的数学期望(保留两位小数).
附:①决定系数R2=1-≈4.1.
19.(17分)某公司研发了一种帮助家长解决孩子早教问题的萌宠机器人.萌宠机器人语音功能让它就像孩子的小伙伴一样和孩子交流,记忆功能还可以记住孩子的使用习惯,很快找到孩子想听的内容.同时提供快乐儿歌、国学经典、启蒙英语等早期教育内容,且云端内容可以持续更新.萌宠机器人一投放市场就受到了很多家长的欢迎.为了更好地服务广大家长,该公司研究部门从流水线上随机抽取100件萌宠机器人(以下简称产品),统计其性能指数并绘制频率直方图(如图1):
产品的性能指数在[50,70)内适合托班幼儿使用(简称A类产品),在[70,90)内适合小班和中班幼儿使用(简称B类产品),在[90,110]内适合大班幼儿使用(简称C类产品),A,B,C三类产品的销售利润分别为每件1.5元,3.5元,5.5元.以这100件产品的性能指数位于各区间的频率代替产品的性能指数位于该区间的概率.
(1)求每件产品的平均销售利润;
(2)该公司为了解年营销费用x(单位:万元)对年销售量y(单位:万件)的影响,对近5年的年营销费用xi和年销售量yi(i=1,2,3,4,5)的数据做了初步处理,得到散点图(如图2)及一些统计量的值(见下表).
ui vi ) )2
16.30 24.87 0.41 1.64
表中ui=lnxi,vi=lnyi,
根据散点图可知,y=a·xb可以作为年销售量y(万件)关于年营销费用x(万元)的回归方程.
①求y关于x的回归方程;
②用①中的回归方程估计该公司应投入多少万元的营销费用,才能使得该产品一年的收益达到最大.(收益=销售利润-营销费用)
参考公式:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其经验回归直线.
参考数据:取e4.159=64.
答案与解析
第9章 统计
1.B 2.A 3.D 4.A 5.D 6.B
7.B 8.C 9.ABC 10.AC 11.ABD
1.B 从题图中可以看出A点较其他点偏离直线,故去掉A点后,拟合效果更好,故决定系数R2会变大,残差平方和变小,|r|会更接近于1,由题图可得x与y正相关,故r会更接近于1,即样本相关系数r的值变大,x与y的相关性变强,故A,C,D错误,B正确.
故选B.
2.A 因为χ2=≈11.54>10.828,所以有99.9%的把握认为学生的学习积极性与对待班级工作的态度有关系,故选A.
3.D 经验回归直线必过样本点的中心,但样本点可能都不在经验回归直线上,故A错误;
若所有样本点都在经验回归直线上,则变量间的样本相关系数为±1,故B错误;
若所有的样本点都在经验回归直线上,则的值与yi相等,故C错误;
样本相关系数r与的符号相同,若经验回归直线>0,则r>0,样本点分布从左到右是上升的,故变量x与y正相关,故D正确.
故选D.
4.A 由题可知,经验回归直线过样本点的中心(10,8),所以将(10,8)代入,可得8=-3×10+,解得=38,当x=9时,=-3×9+38=11,所以残差为10-11=-1.故选A.
5.D 补全列联表如下:
性别 体育锻炼 合计
喜欢 不喜欢
男 80 40 120
女 30 50 80
合计 110 90 200
对于A,样本中男生所占比例为×100%=60%,故A正确;
对于B,估计该校不喜欢体育锻炼的学生所占比例为×100%=45%,故B正确;
对于C,样本中喜欢体育锻炼的男生比喜欢体育锻炼的女生多80-30=50人,故C正确;
对于D,根据表中数据,得χ2=≈16.498>10.828,
所以有99.9%的把握认为是否喜欢体育锻炼与性别有关,故D错误.
故选D.
6.B 由题意,得×(9+9.2+9.4+9.6+9.8+10)=9.5,
×(100+94+93+90+85+78)=90,
则=-20,
=90+9.5×20=280,则=-20x+280.
设工厂获得利润为L元,则L=(x-5)(-20x+280)=-20(x-9.5)2+405,
当x=9.5时,L取得最大值.
所以当单价定为9.5元时,工厂获得最大利润,故选B.
7.B 设男性人数为k,依题意得2×2列联表如下:
喜爱足球 不喜爱足球 合计
男性 k
女性 2k
合计 3k
所以χ2=,
因为本次调查得出“至少有99.5%的把握认为喜爱足球与性别有关”的结论,
所以χ2≥7.879,即≥7.879,解得k≥11.818 5,而k∈N*,因此kmin=12.故选B.
8.C 由,得ln x-0.5,
令=ln ,则x-0.5,
由题知,=3.5,
因为(2.5,3.5)满足x-0.5,
所以3.5=2.5-0.5,解得=1.6,所以=e1.6x-0.5.
因为=e10.7,所以e1.6x-0.5=e10.7,即1.6x-0.5=10.7,解得x=7.
故选C.
9.ABC 易知A,B,C正确,对分类变量x与y的统计量χ2的观测值x0来说,x0越大,判断“x与y有关系”的把握越大,故D不正确.
故选ABC.
10.AC 对于A,B,设该学校高二年级男生人数为2a,女生人数为a,则学生中喜欢徒步的男生为2a×0.7=1.4a,喜欢徒步的女生为0.4a,不喜欢徒步的男生为2a×0.3=0.6a,不喜欢徒步的女生为0.6a,故A正确,B错误;
对于C,若参加调查的学生总人数为300,则男生有200人,女生有100人,可得2×2列联表如下:
是否喜欢徒步 性别 合计
男 女
喜欢 140 40 180
不喜欢 60 60 120
合计 200 100 300
则χ2==25>6.635,
所以有99%的把握认为喜欢徒步和性别有关,故C正确;
对于D,由A的分析,可得2×2列联表如下:
是否喜欢徒步 性别 合计
男 女
喜欢 1.4a 0.4a 1.8a
不喜欢 0.6a 0.6a 1.2a
合计 2a a 3a
则χ2==0.25a,不能判断0.25a与6.635的大小关系,故D错误.
故选AC.
11.ABD 对于A,因为=24,所以=81,所以=9,
则=9,所以m+n=17,故A正确;
对于B,因为=13,
r=,
)2=(8-13)2+(10-13)2+(12-13)2+(14-13)2+(16-13)2+(18-13)2=70,
所以=40,
所以,故B正确;
对于C,因为,所以C错误;
对于D,由上述分析知,
所以ε1+ε2=m+n-18=-1,故D正确.
故选ABD.
12.答案 -0.998
解析 由题意得,=-2×10+59.5,
解得m=62,故.
易得=1 192,=7 020,
所以样本相关系数r=≈-0.998.
13.答案 -0.3;0.98
解析 ∵经验回归直线必过样本点的中心(),
∴5=8=-0.3.对f=cWk两边同时取自然对数,得ln f=ln c+kln W,又xi=ln Wi,yi=ln fi,
∴ln f=ln c+kln W即为y=ln c+kx,
∴k==-0.3.
R2≈1-=0.98.
14.答案 46
解析 依题意,得χ2≥6.635,
故≥6.635,
整理,得(100a-4 000)2≥265 400,即(10a-400)2≥2 654,
因为40≤a≤50且a∈N*,
所以10a-400≥≈45.2,
又a=a0,所以a0的最小值为46.
15.解析 (1)补全2×2列联表如下:
满意 不满意 合计
男 440 60 500
女 460 40 500
合计 900 100 1 000
(1分)
则χ2=≈4.444>3.841,(4分)
故有95%的把握认为消费者对新产品的满意度与性别有关.(5分)
(2)由题意得,X的可能取值为0,1,2,3,
由题表可得,从该地区的消费者中随机抽取1人,不满意的概率为,(7分)
则P(X=0)=.
P(X=2)=,(11分)
所以X的概率分布为
X 0 1 2 3
P
所以E(X)=0×.(13分)
16.解析 (1)由题表,得=87,(2分)
又xi(i=1,2,3,…,5)的方差为)2=200,(3分)
∴=1.07,(6分)
因此=87-1.07×50=33.5,(7分)
∴=140.5,
故预测每天课后自主学习数学的时间为100分钟时的数学成绩是140.5分.(9分)
(2)提出假设H0:学生周末自主学习与成绩进步无关,(10分)
根据题中表2的数据,得χ2=≈12.22>10.828,(13分)
∴有99.9%的把握认为“周末自主学习与成绩进步”有关.(15分)
17.解析 (1)由题意,估计该市流感感染率是=0.3.(2分)
(2)根据题意,得2×2列联表如下:
疫苗情况 流感情况 合计
患有流感 不患有流感
注射疫苗 220 580 800
没注射疫苗 80 120 200
合计 300 700 1 000
(4分)
则χ2=≈11.9>10.828,(6分)
所以有99.9%的把握认为注射流感疫苗与预防流感有关.(7分)
(3)设事件A为“一次检测结果呈阳性”,事件B为“被检测者确实患有流感”,
由题意得,P(B)=0.3,P(A|B)=0.95,P(A|)=0.01,
所以P(AB)=P(B)·P(A|B)=0.3×0.95=0.285,P()=0.7,(10分)
由全概率公式得P(A)=P(B)·P(A|B)+P()=0.3×0.95+0.7×0.01=0.292,(13分)
则P(B|A)=≈0.976,
所以此人真的患有流感的概率约为0.976.(15分)
18.解析 (1)由题表得182.4>79.2,
即,(2分)
所以模型①的决定系数小于模型②的决定系数,说明回归模型②的拟合精度更高、更可靠.(3分)
当x=17时,-14.4≈21.3×4.1-14.4=72.93.
所以预测该企业对产品研发的投入为17亿元时的直接收益是72.93亿元.(5分)
(2)当x>17时,由已知可得=7.2,
所以=67.2,
所以=67.2+0.7×23=83.3,(8分)
所以当x>17时,y与x满足的经验回归方程为=-0.7x+83.3.
当x=20时,=-0.7×20+83.3=69.3.(10分)
所以当x=20时,实际收益的预测值为69.3+10=79.3(亿元),
因为79.3>72.93,所以研发投入20亿元时公司的实际收益更大.(12分)
(3)因为P(0.52-0.02所以P(X>0.50)=0.5+=0.977 2,P(X≤0.50)=1-P(X>0.50)=0.022 8,
因为P(0.52-0.01所以P(X>0.53)=0.5-=0.158 7,
所以P(0.50设每件F产品获得的奖励为Y万元,则Y的概率分布为
Y 0 2 5
P 0.022 8 0.818 5 0.158 7
所以E(Y)=0×0.022 8+2×0.818 5+5×0.158 7≈2.43(万元).(17分)
19.解析 (1)设每件产品的销售利润为ξ元,则ξ的所有可能取值为1.5,3.5,5.5,(1分)
由题图1可得,A,B,C三类产品的频率分别为0.15,0.45,0.4,
所以P(ξ=1.5)=0.15,P(ξ=3.5)=0.45,P(ξ=5.5)=0.4,
所以随机变量ξ的概率分布为
ξ 1.5 3.5 5.5
P 0.15 0.45 0.4
所以E(ξ)=1.5×0.15+3.5×0.45+5.5×0.4=4.
所以每件产品的平均销售利润为4元.(5分)
(2)①由y=a·xb得,ln y=ln(a·xb)=ln a+bln x,
因为u=ln x,v=ln y,所以v=ln a+bu,
由题表中的数据可得,=0.25,
则ln =4.159,(8分)
因为e4.159=64,所以,
故所求的回归方程为.(10分)
②设年收益为z万元,则-x,(11分)
设t=,则f(t)=256t-t4,
所以f'(t)=256-4t3=4(64-t3),(13分)
当t∈(0,4)时, f'(t)>0, f(t)在(0,4)上单调递增,
当t∈(4,+∞)时, f'(t)<0, f(t)在(4,+∞)上单调递减,(15分)
所以当t=4,即x=256时,有最大值,
即估计该公司投入256万元营销费用,才能使得该产品一年的收益达到最大.(17分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025苏教版高中数学选择性必修第二册
第9章 统计
全卷满分150分 考试用时120分钟
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.某公司收集了某商品销售收入y(万元)与相应的广告支出x(万元)的10组数据(xi,yi)(i=1,2,3,…,10),绘制出如下散点图,并利用线性回归模型进行拟合.
若去掉A点后再重新进行线性回归分析,则下列说法正确的是( )
A.决定系数R2变小
B.残差平方和变小
C.样本相关系数r的值变小
D.x与y的相关性变弱
2.某班班主任对全班50名学生学习积极性与对待班级工作的态度进行了调查,统计数据如下表所示:
主动参加班级工作 不太主动参加班级工作 合计
学习积极性高 18 7 25
学习积极性一般 6 19 25
合计 24 26 50
则以下说法正确的是( )
附:χ2=,其中n=a+b+c+d.
P(χ2≥x0) 0.05 0.025 0.010 0.005 0.001
x0 3.841 5.024 6.635 7.879 10.828
A.有99.9%的把握认为学生的学习积极性与对待班级工作的态度有关系
B.有99.5%的把握认为学生的学习积极性与对待班级工作的态度没有关系
C.有99%的把握认为学生的学习积极性与对待班级工作的态度没有关系
D.没有充分的证据显示学生的学习积极性与对待班级工作的态度有关系
3.根据最小二乘法求得一组样本数据(xi,yi)(其中i=1,2,…,300)的经验回归方程是,则下列说法正确的是( )
A.至少有一个样本点落在经验回归直线上
B.若所有样本点都在经验回归直线上,则变量间的样本相关系数为1
C.对所有的变量xi(i=1,2,…,300),的值一定与yi有误差
D.若经验回归直线>0,则变量x与y正相关
4.为维护市场秩序,保护消费者权益,在十一假期来临之际,某市物价部门对某商品在5家商场的售价x(元)及其一天的销售量y(件)进行调查,得到五组数据(xi,yi)(i=1,2,3,4,5),经过分析、计算,得=8,y关于x的经验回归方程为,则相应于点(9,10)的残差为( )
A.-1 B.1 C.-3 D.3
5.为促进学生积极参加体育锻炼,养成良好的锻炼习惯,提高体质健康水平,某学校从全校学生中随机抽取200名学生进行“是否喜欢体育锻炼”的问卷调查,统计结果如下表:
性别 体育锻炼 合计
喜欢 不喜欢
男
女 50 80
合计 110
附:χ2=,其中n=a+b+c+d.
P(χ2≥x0) 0.05 0.025 0.010 0.005 0.001
x0 3.841 5.024 6.635 7.879 10.828
下列结论不正确的是( )
A.样本中男生所占比例为60%
B.估计该校不喜欢体育锻炼的学生所占比例为45%
C.样本中喜欢体育锻炼的男生比喜欢体育锻炼的女生多50人
D.没有99.9%的把握认为是否喜欢体育锻炼与性别有关
6.某工厂为了对研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价x/元 9 9.2 9.4 9.6 9.8 10
销量y/件 100 94 93 90 85 78
预计在今后的销售中,销量与单价仍然满足这种线性相关关系,且该产品的成本是5元/件,为使工厂获得最大利润,该产品的单价应定为( )
参考公式:对于一组数据(x1,y1),(x2,y2),…,(xn,yn),其经验回归直线.
参考数据:.
A.9.4元 B.9.5元
C.9.6元 D.9.7元
7.为了解喜爱足球是否与性别有关,随机抽取了若干人进行调查,抽取女性人数是男性人数的2倍,男性喜爱足球的人数占男性人数的,若本次调查得出“至少有99.5%的把握认为喜爱足球与性别有关”的结论,则被调查的男性至少有( )
附:χ2=,其中n=a+b+c+d.
P(χ2≥x0) 0.10 0.05 0.010 0.005 0.001
x0 2.706 3.841 6.635 7.879 10.828
A.11人 B.12人 C.13人 D.14人
8.已知变量y关于变量x的回归方程为=e10.7,则x=( )
x 1 2 3 4
y e e3 e4 e6
A.5 B.6 C.7 D.8
二、多项选择题(本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分)
9.下列说法正确的是( )
A.在回归分析中,残差的平方和越小,模型的拟合效果越好
B.在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适
C.若数据x1,x2,…,xn的平均数为1,则2x1,2x2,…,2xn的平均数为2
D.对分类变量x与y的统计量χ2的观测值x0来说,x0越小,判断“x与y有关系”的把握越大
10.已知某学校高二年级男生人数是女生人数的2倍,该年级全部男、女生是否喜欢徒步运动的等高堆积条形图如图,下列说法正确的是( )
附:χ2=,其中n=a+b+c+d.
P(χ2≥x0) 0.10 0.05 0.010
x0 2.706 3.841 6.635
A.参加调查的学生中喜欢徒步的男生比喜欢徒步的女生多
B.参加调查的学生中不喜欢徒步的男生比不喜欢徒步的女生少
C.若参加调查的学生总人数为300,则有99%的把握认为喜欢徒步和性别有关
D.无论参加调查的学生总人数为多少,都有99%的把握认为喜欢徒步和性别有关
11.某农科所针对耕种深度x(单位:cm)与水稻每公顷产量y(单位:t)的关系进行研究,所得部分数据如下表:
耕种深度x/cm 8 10 12 14 16 18
每公顷产量y/t 6 8 m n 11 12
已知m
参考公式:在经验回归方程中,.
A.m+n=17 B.
C. D.ε1+ε2=-1
三、填空题(本题共3小题,每小题5分,共15分)
12.已知一组数据(18,24),(13,34),(10,38),(-1,m)的经验回归方程为=-2x+59.5,则该组数据的样本相关系数r= (精确到0.001).
13.某校数学建模兴趣小组收集了一组恒温动物体重W(单位:克)与其脉搏率f(单位:次/分钟)的对应数据(Wi,fi)(i=1,2,…,8),根据生物学常识和散点图得出f与W近似满足f=cWk(c,k为参数).令xi=lnWi,yi=lnfi,计算得=214.由最小二乘法得经验回归方程为x+7.4,则k的值为 ;为判断拟合效果,通过经验回归方程求得预测值(i=1,2,…,8),若残差平方和)2≈0.28,则决定系数R2= .
参考公式:决定系数R2=1-.
14.新疆某农科所为了研究不同土壤环境下棉花的品质,选取了甲、乙两块试验田进行种植.在棉花成熟后采摘,分别从甲、乙两块试验田采摘的棉花中各随机抽取50份样本,测定其马克隆值,整理测量数据得到如下2×2列联表(单位:份),其中40≤a≤50且a∈N*.
注:棉花的马克隆值是反映棉花纤维细度与成熟度的综合指标,是棉花纤维重要的内在质量指标之一.根据国家标准规定,马克隆值可分为A,B,C三个级别,A级品质最好,B级品质为标准,C级品质最差.
A级或B级 C级 合计
甲试验田 a 50-a 50
乙试验田 80-a a-30 50
合计 80 20 100
当a=a0时,至少有99%的把握认为该品种棉花的马克隆值级别与土壤环境有关,则a0的最小值为 .
附:χ2=,其中n=a+b+c+d.
P(χ2≥x0) 0.05 0.010 0.001
x0 3.841 6.635 10.828
四、解答题(本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤)
15.(13分)甲公司推出一种新产品,为了解某地区消费者对新产品的满意度,从中随机调查了1000名消费者,得到下表:
满意 不满意
男 440 60
女 460 40
(1)能否有95%的把握认为消费者对新产品的满意度与性别有关
(2)若用频率估计概率,从该地区消费者中随机选取3人,用X表示不满意的人数,求X的概率分布与数学期望.
附:χ2=,其中n=a+b+c+d.
P(χ2≥x0) 0.10 0.05 0.010
x0 2.706 3.841 6.635
16.(15分)为了了解高中学生每天课后自主学习数学的时间x(分钟)和他们的数学成绩y(分)的关系,某试验小组做了调查,得到一些数据(表1).
表1
编号 1 2 3 4 5
学习时间x/分钟 30 40 50 60 70
数学成绩y/分 65 78 85 99 108
(1)经分析,可用线性回归模型拟合y与x的关系,请求出经验回归方程,并由此预测每天课后自主学习数学的时间为100分钟时的数学成绩;
(2)根据上述调查,某校提倡学生周末自主学习.经过一学期的实施后,抽样调查了220名学生.按照是否参与周末自主学习以及成绩是否有进步进行统计,得到2×2列联表(表2).依据表中数据,判断是否有99.9%的把握认为“周末自主学习与成绩进步”有关.
表2
成绩没有进步 成绩有进步 合计
参与周末 自主学习 35 130 165
未参与周末 自主学习 25 30 55
合计 60 160 220
附:①yi=435,xi的方差为200;
②在经验回归方程;
③χ2=,其中n=a+b+c+d.
P(χ2≥x0) 0.10 0.05 0.010 0.005 0.001
x0 2.706 3.841 6.635 7.879 10.828
17.(15分)春季流感对人们的健康生活带来了一定的影响,为了有效预防流感,很多人注射了流感疫苗.某市防疫部门从辖区居民中随机抽取了1000人进行调查,发现其中注射疫苗的800人中有220人感染流感,另外没注射疫苗的200人中有80人感染流感.医学研究表明,流感的检测结果是有错检的可能,已知患有流感的人其检测结果有95%的可能呈阳性(感染),而没有患流感的人其检测结果有99%的可能呈阴性(未感染).
(1)估计该市流感感染率是多少;
(2)根据所给数据,判断是否有99.9%的把握认为注射流感疫苗与预防流感有关;
(3)已知某人的流感检测结果呈阳性,求此人真的患有流感的概率.(精确到0.001)
附:χ2=,其中n=a+b+c+d.
P(χ2≥x0) 0.10 0.05 0.010 0.005 0.001
x0 2.706 3.841 6.635 7.879 10.828
18.(17分)某大型企业对其产品进行研发与创新,根据市场调研与模拟,得到研发投入x(亿元)与研发创新的直接收益y(亿元)的数据统计如下:
x 2 3 4 6 8 10 13 21 22 23 24 25
y 13 22 31 42 50 56 58 68.5 68 67.5 66 66
当0
回归方程 =4.1x+11.8 -14.4
)2 182.4 79.2
(2)为鼓励科技创新,当研发的投入不少于20亿元时,国家给予公司补贴收益10亿元,以经验回归方程为预测依据,比较研发投入17亿元与20亿元时公司实际收益的大小;
(3)研发改造后,该公司F产品的效率X大幅提高,X服从正态分布N(0.52,0.012),公司对研发团队的奖励方案如下:若F产品的效率不超过50%,不予奖励;若F产品的效率超过50%但不超过53%,每件F产品奖励2万元;若F产品的效率超过53%,每件F产品奖励5万元.求每件F产品获得奖励的数学期望(保留两位小数).
附:①决定系数R2=1-≈4.1.
19.(17分)某公司研发了一种帮助家长解决孩子早教问题的萌宠机器人.萌宠机器人语音功能让它就像孩子的小伙伴一样和孩子交流,记忆功能还可以记住孩子的使用习惯,很快找到孩子想听的内容.同时提供快乐儿歌、国学经典、启蒙英语等早期教育内容,且云端内容可以持续更新.萌宠机器人一投放市场就受到了很多家长的欢迎.为了更好地服务广大家长,该公司研究部门从流水线上随机抽取100件萌宠机器人(以下简称产品),统计其性能指数并绘制频率直方图(如图1):
产品的性能指数在[50,70)内适合托班幼儿使用(简称A类产品),在[70,90)内适合小班和中班幼儿使用(简称B类产品),在[90,110]内适合大班幼儿使用(简称C类产品),A,B,C三类产品的销售利润分别为每件1.5元,3.5元,5.5元.以这100件产品的性能指数位于各区间的频率代替产品的性能指数位于该区间的概率.
(1)求每件产品的平均销售利润;
(2)该公司为了解年营销费用x(单位:万元)对年销售量y(单位:万件)的影响,对近5年的年营销费用xi和年销售量yi(i=1,2,3,4,5)的数据做了初步处理,得到散点图(如图2)及一些统计量的值(见下表).
ui vi ) )2
16.30 24.87 0.41 1.64
表中ui=lnxi,vi=lnyi,
根据散点图可知,y=a·xb可以作为年销售量y(万件)关于年营销费用x(万元)的回归方程.
①求y关于x的回归方程;
②用①中的回归方程估计该公司应投入多少万元的营销费用,才能使得该产品一年的收益达到最大.(收益=销售利润-营销费用)
参考公式:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其经验回归直线.
参考数据:取e4.159=64.
答案与解析
第9章 统计
1.B 2.A 3.D 4.A 5.D 6.B
7.B 8.C 9.ABC 10.AC 11.ABD
1.B 从题图中可以看出A点较其他点偏离直线,故去掉A点后,拟合效果更好,故决定系数R2会变大,残差平方和变小,|r|会更接近于1,由题图可得x与y正相关,故r会更接近于1,即样本相关系数r的值变大,x与y的相关性变强,故A,C,D错误,B正确.
故选B.
2.A 因为χ2=≈11.54>10.828,所以有99.9%的把握认为学生的学习积极性与对待班级工作的态度有关系,故选A.
3.D 经验回归直线必过样本点的中心,但样本点可能都不在经验回归直线上,故A错误;
若所有样本点都在经验回归直线上,则变量间的样本相关系数为±1,故B错误;
若所有的样本点都在经验回归直线上,则的值与yi相等,故C错误;
样本相关系数r与的符号相同,若经验回归直线>0,则r>0,样本点分布从左到右是上升的,故变量x与y正相关,故D正确.
故选D.
4.A 由题可知,经验回归直线过样本点的中心(10,8),所以将(10,8)代入,可得8=-3×10+,解得=38,当x=9时,=-3×9+38=11,所以残差为10-11=-1.故选A.
5.D 补全列联表如下:
性别 体育锻炼 合计
喜欢 不喜欢
男 80 40 120
女 30 50 80
合计 110 90 200
对于A,样本中男生所占比例为×100%=60%,故A正确;
对于B,估计该校不喜欢体育锻炼的学生所占比例为×100%=45%,故B正确;
对于C,样本中喜欢体育锻炼的男生比喜欢体育锻炼的女生多80-30=50人,故C正确;
对于D,根据表中数据,得χ2=≈16.498>10.828,
所以有99.9%的把握认为是否喜欢体育锻炼与性别有关,故D错误.
故选D.
6.B 由题意,得×(9+9.2+9.4+9.6+9.8+10)=9.5,
×(100+94+93+90+85+78)=90,
则=-20,
=90+9.5×20=280,则=-20x+280.
设工厂获得利润为L元,则L=(x-5)(-20x+280)=-20(x-9.5)2+405,
当x=9.5时,L取得最大值.
所以当单价定为9.5元时,工厂获得最大利润,故选B.
7.B 设男性人数为k,依题意得2×2列联表如下:
喜爱足球 不喜爱足球 合计
男性 k
女性 2k
合计 3k
所以χ2=,
因为本次调查得出“至少有99.5%的把握认为喜爱足球与性别有关”的结论,
所以χ2≥7.879,即≥7.879,解得k≥11.818 5,而k∈N*,因此kmin=12.故选B.
8.C 由,得ln x-0.5,
令=ln ,则x-0.5,
由题知,=3.5,
因为(2.5,3.5)满足x-0.5,
所以3.5=2.5-0.5,解得=1.6,所以=e1.6x-0.5.
因为=e10.7,所以e1.6x-0.5=e10.7,即1.6x-0.5=10.7,解得x=7.
故选C.
9.ABC 易知A,B,C正确,对分类变量x与y的统计量χ2的观测值x0来说,x0越大,判断“x与y有关系”的把握越大,故D不正确.
故选ABC.
10.AC 对于A,B,设该学校高二年级男生人数为2a,女生人数为a,则学生中喜欢徒步的男生为2a×0.7=1.4a,喜欢徒步的女生为0.4a,不喜欢徒步的男生为2a×0.3=0.6a,不喜欢徒步的女生为0.6a,故A正确,B错误;
对于C,若参加调查的学生总人数为300,则男生有200人,女生有100人,可得2×2列联表如下:
是否喜欢徒步 性别 合计
男 女
喜欢 140 40 180
不喜欢 60 60 120
合计 200 100 300
则χ2==25>6.635,
所以有99%的把握认为喜欢徒步和性别有关,故C正确;
对于D,由A的分析,可得2×2列联表如下:
是否喜欢徒步 性别 合计
男 女
喜欢 1.4a 0.4a 1.8a
不喜欢 0.6a 0.6a 1.2a
合计 2a a 3a
则χ2==0.25a,不能判断0.25a与6.635的大小关系,故D错误.
故选AC.
11.ABD 对于A,因为=24,所以=81,所以=9,
则=9,所以m+n=17,故A正确;
对于B,因为=13,
r=,
)2=(8-13)2+(10-13)2+(12-13)2+(14-13)2+(16-13)2+(18-13)2=70,
所以=40,
所以,故B正确;
对于C,因为,所以C错误;
对于D,由上述分析知,
所以ε1+ε2=m+n-18=-1,故D正确.
故选ABD.
12.答案 -0.998
解析 由题意得,=-2×10+59.5,
解得m=62,故.
易得=1 192,=7 020,
所以样本相关系数r=≈-0.998.
13.答案 -0.3;0.98
解析 ∵经验回归直线必过样本点的中心(),
∴5=8=-0.3.对f=cWk两边同时取自然对数,得ln f=ln c+kln W,又xi=ln Wi,yi=ln fi,
∴ln f=ln c+kln W即为y=ln c+kx,
∴k==-0.3.
R2≈1-=0.98.
14.答案 46
解析 依题意,得χ2≥6.635,
故≥6.635,
整理,得(100a-4 000)2≥265 400,即(10a-400)2≥2 654,
因为40≤a≤50且a∈N*,
所以10a-400≥≈45.2,
又a=a0,所以a0的最小值为46.
15.解析 (1)补全2×2列联表如下:
满意 不满意 合计
男 440 60 500
女 460 40 500
合计 900 100 1 000
(1分)
则χ2=≈4.444>3.841,(4分)
故有95%的把握认为消费者对新产品的满意度与性别有关.(5分)
(2)由题意得,X的可能取值为0,1,2,3,
由题表可得,从该地区的消费者中随机抽取1人,不满意的概率为,(7分)
则P(X=0)=.
P(X=2)=,(11分)
所以X的概率分布为
X 0 1 2 3
P
所以E(X)=0×.(13分)
16.解析 (1)由题表,得=87,(2分)
又xi(i=1,2,3,…,5)的方差为)2=200,(3分)
∴=1.07,(6分)
因此=87-1.07×50=33.5,(7分)
∴=140.5,
故预测每天课后自主学习数学的时间为100分钟时的数学成绩是140.5分.(9分)
(2)提出假设H0:学生周末自主学习与成绩进步无关,(10分)
根据题中表2的数据,得χ2=≈12.22>10.828,(13分)
∴有99.9%的把握认为“周末自主学习与成绩进步”有关.(15分)
17.解析 (1)由题意,估计该市流感感染率是=0.3.(2分)
(2)根据题意,得2×2列联表如下:
疫苗情况 流感情况 合计
患有流感 不患有流感
注射疫苗 220 580 800
没注射疫苗 80 120 200
合计 300 700 1 000
(4分)
则χ2=≈11.9>10.828,(6分)
所以有99.9%的把握认为注射流感疫苗与预防流感有关.(7分)
(3)设事件A为“一次检测结果呈阳性”,事件B为“被检测者确实患有流感”,
由题意得,P(B)=0.3,P(A|B)=0.95,P(A|)=0.01,
所以P(AB)=P(B)·P(A|B)=0.3×0.95=0.285,P()=0.7,(10分)
由全概率公式得P(A)=P(B)·P(A|B)+P()=0.3×0.95+0.7×0.01=0.292,(13分)
则P(B|A)=≈0.976,
所以此人真的患有流感的概率约为0.976.(15分)
18.解析 (1)由题表得182.4>79.2,
即,(2分)
所以模型①的决定系数小于模型②的决定系数,说明回归模型②的拟合精度更高、更可靠.(3分)
当x=17时,-14.4≈21.3×4.1-14.4=72.93.
所以预测该企业对产品研发的投入为17亿元时的直接收益是72.93亿元.(5分)
(2)当x>17时,由已知可得=7.2,
所以=67.2,
所以=67.2+0.7×23=83.3,(8分)
所以当x>17时,y与x满足的经验回归方程为=-0.7x+83.3.
当x=20时,=-0.7×20+83.3=69.3.(10分)
所以当x=20时,实际收益的预测值为69.3+10=79.3(亿元),
因为79.3>72.93,所以研发投入20亿元时公司的实际收益更大.(12分)
(3)因为P(0.52-0.02
因为P(0.52-0.01
所以P(0.50
Y 0 2 5
P 0.022 8 0.818 5 0.158 7
所以E(Y)=0×0.022 8+2×0.818 5+5×0.158 7≈2.43(万元).(17分)
19.解析 (1)设每件产品的销售利润为ξ元,则ξ的所有可能取值为1.5,3.5,5.5,(1分)
由题图1可得,A,B,C三类产品的频率分别为0.15,0.45,0.4,
所以P(ξ=1.5)=0.15,P(ξ=3.5)=0.45,P(ξ=5.5)=0.4,
所以随机变量ξ的概率分布为
ξ 1.5 3.5 5.5
P 0.15 0.45 0.4
所以E(ξ)=1.5×0.15+3.5×0.45+5.5×0.4=4.
所以每件产品的平均销售利润为4元.(5分)
(2)①由y=a·xb得,ln y=ln(a·xb)=ln a+bln x,
因为u=ln x,v=ln y,所以v=ln a+bu,
由题表中的数据可得,=0.25,
则ln =4.159,(8分)
因为e4.159=64,所以,
故所求的回归方程为.(10分)
②设年收益为z万元,则-x,(11分)
设t=,则f(t)=256t-t4,
所以f'(t)=256-4t3=4(64-t3),(13分)
当t∈(0,4)时, f'(t)>0, f(t)在(0,4)上单调递增,
当t∈(4,+∞)时, f'(t)<0, f(t)在(4,+∞)上单调递减,(15分)
所以当t=4,即x=256时,有最大值,
即估计该公司投入256万元营销费用,才能使得该产品一年的收益达到最大.(17分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
