2025苏教版高中数学选择性必修第二册强化练习题(含解析)--第9章 统计复习提升
文档属性
| 名称 | 2025苏教版高中数学选择性必修第二册强化练习题(含解析)--第9章 统计复习提升 |

|
|
| 格式 | docx | ||
| 文件大小 | 445.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-15 18:54:46 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025苏教版高中数学选择性必修第二册
本章复习提升
易混易错练
易错点1 选错回归模型致错
1.(2024江苏常州高级中学期末)某公司为了了解年研发资金投入金额x(单位:亿元)对年销售额y(单位:亿元)的影响,对公司近12年的年研发资金投入金额和年销售额的数据进行了对比分析,建立了两个模型:①y=α+βx2,②y=eλx+t,其中α,β,λ,t均为常数,e为自然对数的底数,并得到一些统计量的值.令ui=,vi=ln yi,i=1,2,3,…,12,经计算得如下数据:
)2 )2
22 66 77 2
)2 )2
460 5 31 250 3.08
) )
220 14
(1)请从样本相关系数的角度,分析哪一个模型拟合效果更好;
(2)根据(1)中分析及表中数据,求y关于x的回归方程.
附:样本相关系数r=;经验回归方程x中,.
2.某农科所发现,一种作物的年收获量s(单位:kg)与“相近”作物株数n具有相关关系(两株作物“相近”是指它们的直线距离不超过1 m),并分别记录了“相近”作物株数为1,2,3,5,6,7时,该作物的年收获量的相关数据如下表:
n 1 2 3 5 6 7
s 60 55 53 46 45 41
(1)根据研究发现,该作物的年收获量s和“相近”作物株数n有以下两种可能的回归方程:①;②.利用统计知识,结合样本相关系数r比较使用哪种回归方程更合适;
(2)如图所示,农科所在正方形地块的每个格点(指横、纵直线的交叉点)处都种了一株该作物,其中每个小正方形的面积为1 m2,若在所种作物中随机选取一株,求它的年收获量的概率分布与数学期望.(注:年收获量以(1)中选择的回归方程计算所得数据为依据)
参考公式:经验回归方程为,其中,样本相关系数r=.
参考数据:≈2.65,≈43,其中wi=.
易错点2 用错公式致错
3.(2024江苏淮安马坝高级中学学情调研)某商场统计了2022年1月~5月某商品的线上月销售量y(单位:千件)与售价x(单位:元/件)的情况如下表所示.
月份 1 2 3 4 5
售价x/ (元/件) 60 56 58 57 54
月销售量 y/千件 5 9 7 10 9
(1)求样本相关系数r,并说明是否可以用线性回归模型拟合y与x的关系(当|r|∈[0.75,1]时,可以认为两个变量有很强的线性相关性;否则,没有很强的线性相关性.结果精确到0.01);
(2)建立y关于x的经验回归方程,并估计当售价为55元/件时,该商品的线上月销售量为多少千件;
(3)若每件商品的进价为(0.5x+25)元,不考虑其他费用,由(2)中结论,当商品售价为多少时,可使得该商品的月利润最大 (结果保留整数)
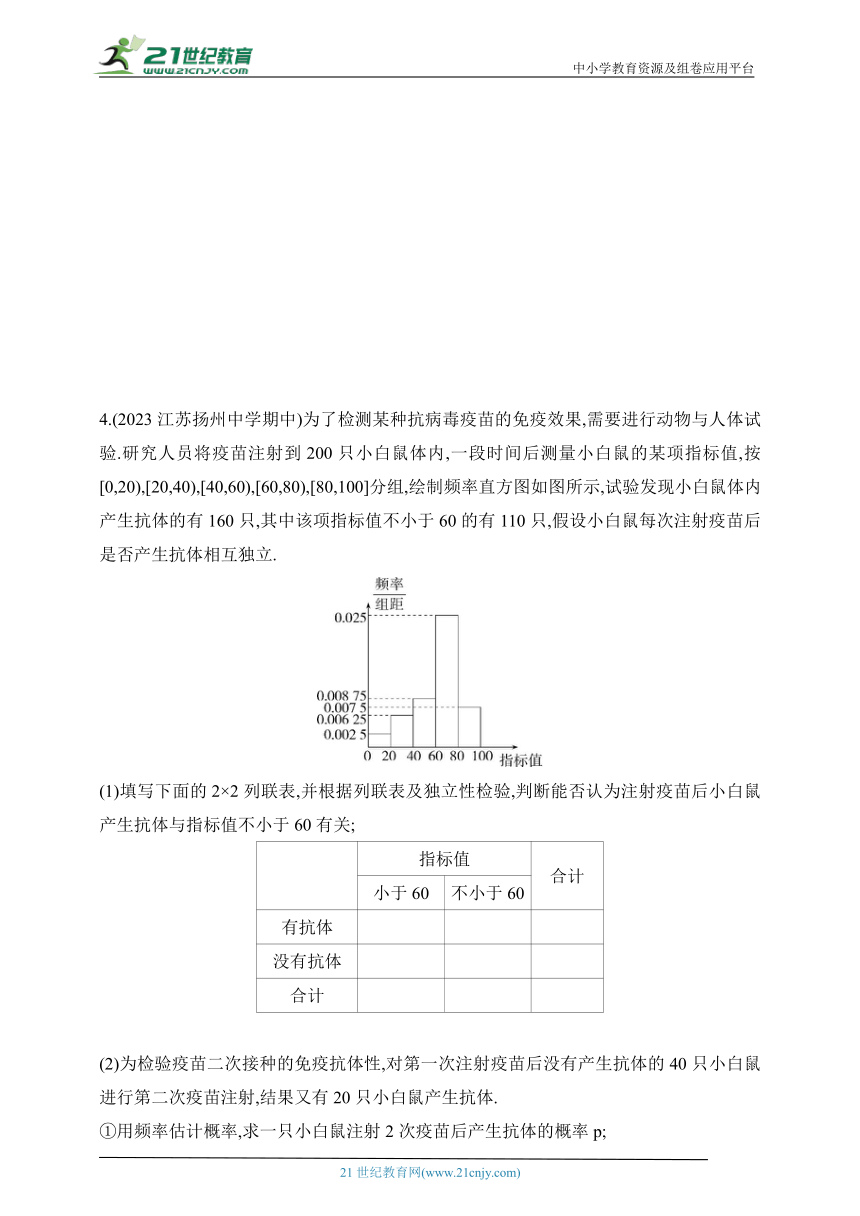
4.(2023江苏扬州中学期中)为了检测某种抗病毒疫苗的免疫效果,需要进行动物与人体试验.研究人员将疫苗注射到200只小白鼠体内,一段时间后测量小白鼠的某项指标值,按[0,20),[20,40),[40,60),[60,80),[80,100]分组,绘制频率直方图如图所示,试验发现小白鼠体内产生抗体的有160只,其中该项指标值不小于60的有110只,假设小白鼠每次注射疫苗后是否产生抗体相互独立.
(1)填写下面的2×2列联表,并根据列联表及独立性检验,判断能否认为注射疫苗后小白鼠产生抗体与指标值不小于60有关;
指标值 合计
小于60 不小于60
有抗体
没有抗体
合计
(2)为检验疫苗二次接种的免疫抗体性,对第一次注射疫苗后没有产生抗体的40只小白鼠进行第二次疫苗注射,结果又有20只小白鼠产生抗体.
①用频率估计概率,求一只小白鼠注射2次疫苗后产生抗体的概率p;
②以①中确定的概率p作为人体注射2次疫苗后产生抗体的概率,进行人体接种试验,记n个人注射2次疫苗后产生抗体的人数为X.试验后统计数据显示,当X=99时,P(X)取最大值,求参加人体接种试验的人数n.
参考公式: χ2=,其中n=a+b+c+d.
参考数据:
P(χ2≥x0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025
x0 0.455 0.708 1.323 2.072 2.706 3.841 5.024
思想方法练
一、函数与方程思想在独立性检验中的应用
1.(2024辽宁朝阳建平实验中学)已知2×2列联表如下:
温度低 于30 ℃ 温度不低 于30 ℃ 合计
高产量 15 m 15+m
低产量 5 15 20
合计 20 15+m 35+m
若χ2=(m>0),则m= .
附: χ2=,其中n=a+b+c+d.
2.(2024湖南大联考模拟)某市教育局为了调查学生热爱数学是否与学生的年级有关,从全市随机抽取了50名高二学生和m(m>50)名高三学生进行调查,每名学生对“是否热爱数学”提出“热爱”或“不热爱”的观点,得到如下数据:
观点 高二 高三
热爱 30 20
不热爱 20
若有99%的把握认为热爱数学与学生的年级有关,则实数m的最小值为 .
附: χ2=,其中n=a+b+c+d.
P(χ2≥x0) 0.050 0.010 0.001
x0 3.841 6.635 10.828
二、数形结合思想在回归分析中的应用
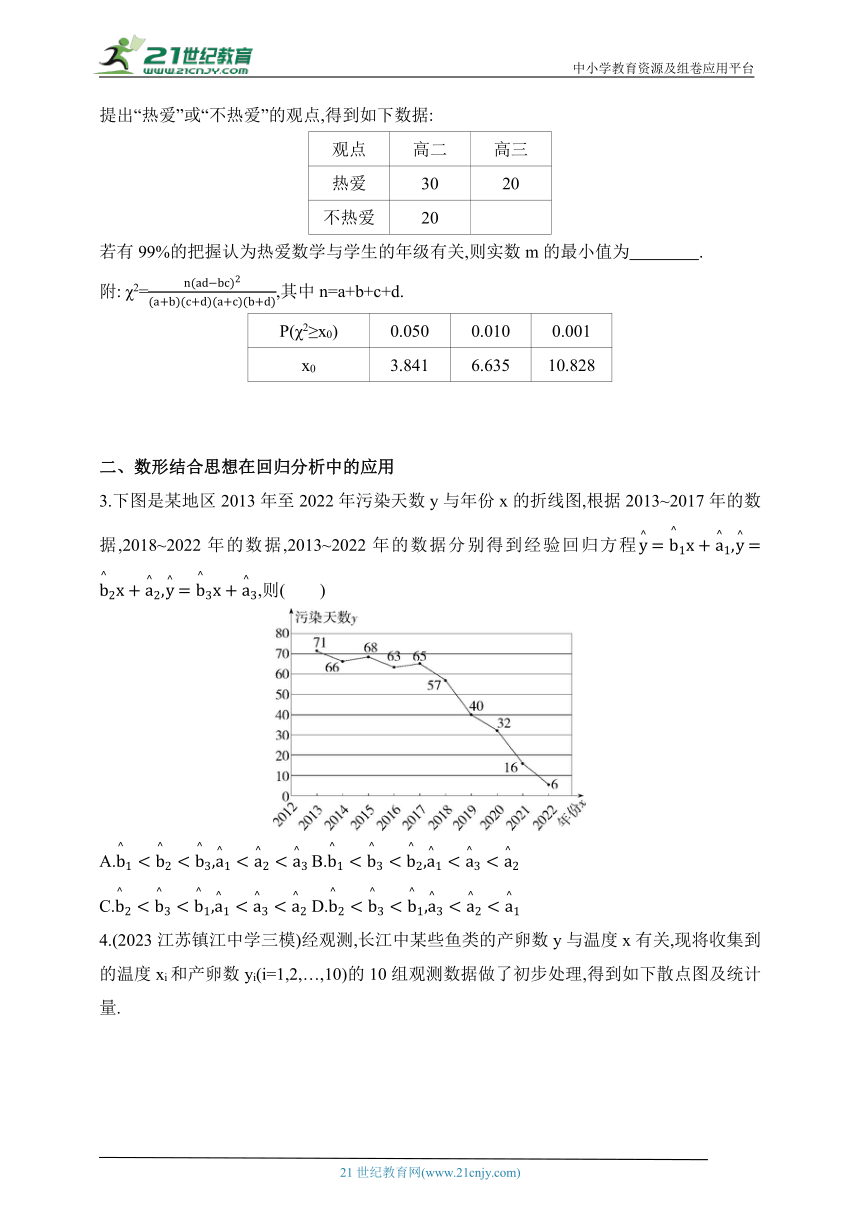
3.下图是某地区2013年至2022年污染天数y与年份x的折线图,根据2013~2017年的数据,2018~2022年的数据,2013~2022年的数据分别得到经验回归方程,则( )
A. B.
C. D.
4.(2023江苏镇江中学三模)经观测,长江中某些鱼类的产卵数y与温度x有关,现将收集到的温度xi和产卵数yi(i=1,2,…,10)的10组观测数据做了初步处理,得到如下散点图及统计量.
xi ti yi zi
360 54.5 1 360 44
)2 )2 )
384 3 588
) )
32 6 430
表中ti=,zi=ln yi,zi.
(1)根据散点图判断,y=a+bx(a,b为常数),y=n+m(x≥0,n,m为常数)与y=c1(c1,c2为常数,且c1>0,c2≠0)哪一个适宜作为y与x之间的回归方程模型,并求出y关于x的回归方程;(给出判断即可,不必说明理由)
(2)某兴趣小组抽取两批鱼卵,已知第一批中共有6个鱼卵,其中死卵有2个;第二批中共有8个鱼卵,其中死卵有3个.现随机挑选一批,然后从该批次中随机取出2个鱼卵,求取出死卵个数的概率分布及数学期望.
附:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其经验回归直线u的斜率和截距的最小二乘估计分别为.
、转化与化归思想在回归分析中的应用
5.(2024江苏南通适应性考试)随着科技的发展,手机的功能已经非常强大,各类App让用户的生活质量得到极大的提升,但是大量的青少年却沉迷于手机游戏,极大地毒害了青少年的身心健康.为了引导青少年抵制不良游戏,适度参与益脑游戏,某游戏公司开发了一款益脑游戏App,在内测时收集了玩家对每一关的平均过关时间,如下表:
关卡x 1 2 3 4 5 6
平均过关 时间y/秒 50 78 124 121 137 352
(1)通过分析,可用模型y=aebx拟合y与x的关系,试求y与x的回归方程;
(2)甲和乙约定举行对战赛,每局比赛通关用时少的人获胜(假设甲、乙都能通关),两人约定先胜4局者赢得比赛.已知甲每局获胜的概率为,乙每局获胜的概率为,若前3局中甲胜2局,乙胜1局,求甲最终赢得比赛的概率.
参考公式:对于一组数据(xi,yi)(i=1,2,3,…,n),其经验回归直线.
参考数据:ui≈28.67,xiui≈106.05,其中ui=ln yi.
6.(2024山东潍坊临朐第一中学月考)某地随着经济的发展,居民收入逐年增长,该地一银行连续五年的储蓄存款(年底余额)数据如表1:
年份x 2013 2014 2015 2016 2017
储蓄存款 y/千亿元 5 6 7 8 10
为了研究计算的方便,工作人员将表1的数据进行了处理,令t=x-2 012,z=y-5,得到表2:
时间代号t 1 2 3 4 5
z 0 1 2 3 5
(1)求z关于t的经验回归方程;
(2)通过(1)中的方程,求出y关于x的经验回归方程;
(3)用所求经验回归方程预测到2024年年底,此银行储蓄存款可达多少.
附:对于经验回归方程.
答案与分层梯度式解析
本章复习提升
易混易错练
1.解析 (1)设模型①和②的样本相关系数分别为r1,r2.
由题意可得,r1==0.88,
r2=≈0.91,
所以|r1|<|r2|,由样本相关系数的性质可得,模型②的拟合效果更好.
(2)因为y=eλx+t,所以ln y=λx+t,
由题知,v=ln y,则v=λx+t,
可得×22=1,
所以v关于x的经验回归方程为x+1,
即y关于x的回归方程为.
2.解析 (1)×(60+55+53+46+45+41)=50,
则)=(-3)×10+(-2)×5+(-1)×3+1×(-4)+2×(-5)+3×(-9)=-84,
)2=(-3)2+(-2)2+(-1)2+12+22+32=28,
)2=102+52+32+(-4)2+(-5)2+(-9)2=256,
设回归方程①和②的样本相关系数分别为r1,r2,则r1=≈-0.991,
令w=n2,则r2≈≈-0.965,
∴|r1|>|r2|,
∴回归方程①更合适.
(2)由(1)知=50+3×4=62,
故所求的经验回归方程为=-3n+62,
结合题中图形可知n的可能取值为2,3,4,代入经验回归方程中可求得与之相对应的s的估计值分别为56,53,50,
则P(s=56)=P(n=2)=,
P(s=53)=P(n=3)=,
P(s=50)=P(n=4)=.
∴年收获量s的概率分布为
s 56 53 50
P
∴E(s)=56×=53.
易错警示 本题易出错的地方有两点:①对样本相关系数的含义理解不准确,选错回归方程致错;②对经验回归方程的含义理解不准确,在解决第(2)问时没有利用第(1)问中的经验回归方程进行估计,而是利用了题表中的数据.
3.解析 (1)由题表中的数据,得=8,
则,
=4,
)=3×(-3)+(-1)×1+1×(-1)+0×2+(-3)×1=-14,
所以r=≈-0.78,
因为|r|>0.75,所以y与x有很强的线性相关性,可以用线性回归模型拟合.
(2)设经验回归方程为=-0.7,
=8-(-0.7)×57=47.9,
所以y关于x的经验回归方程为=-0.7x+47.9,
当x=55时,=-0.7×55+47.9=9.4,
故当售价为55元/件时,该商品的线上月销售量约为9.4千件.
(3)设该商品的月利润为Z元,则Z=1 000(x-0.5x-25)×(-0.7x+47.9)=50(-7x2+829x-23 950),
当x=≈59时,Z取得最大值.
即当商品售价为59元/件时,可使得该商品的月利润最大.
4.解析 (1)由题中的频率直方图,知200只小白鼠按指标值分布如下:
在[0,20)内的有0.002 5×20×200=10(只);
在[20,40)内的有0.006 25×20×200=25(只);
在[40,60)内的有0.008 75×20×200=35(只);
在[60,80)内的有0.025×20×200=100(只);
在[80,100]内的有0.007 5×20×200=30(只).
由题意知有抗体且指标值小于60的有50只,
而指标值小于60的小白鼠共有10+25+35=70(只),
所以指标值小于60且没有抗体的小白鼠有20只,
同理,指标值不小于60且没有抗体的小白鼠有20只,
故2×2列联表如下:
指标值 合计
小于60 不小于60
有抗体 50 110 160
没有抗体 20 20 40
合计 70 130 200
提出假设H0:注射疫苗后小白鼠产生抗体与指标值不小于60无关.
根据列联表中的数据,得χ2=≈4.945,
因为当H0成立时, χ2≥3.841的概率约为0.05,
所以我们有95%的把握认为,注射疫苗后小白鼠产生抗体与指标值不小于60有关.
(2)①设事件A=“小白鼠第一次注射疫苗后产生抗体”,事件B=“小白鼠第二次注射疫苗后产生抗体”,事件C=“小白鼠注射2次疫苗后产生抗体”,
则P(A)==0.5,
P(C)=P(A)+P()P(B)=0.8+0.2×0.5=0.9,
所以一只小白鼠注射2次疫苗后产生抗体的概率p=0.9.
②由题意,知随机变量X~B(n,0.9),
P(X=k)=×0.9k×0.1n-k(k=0,1,2,…,n),
因为P(X=99)最大,
所以
解得109≤n≤110,
因为n是整数,所以n=109或n=110,
所以参加人体接种试验的人数n为109或110.
易错警示 先根据题意准确写出2×2列联表,然后利用公式求出χ2的值,最后根据χ2的估计值选择临界值表中的对应数据进行比较.注意χ2的计算公式中,a,b,c,d的各项要准确对应,不要弄混.
思想方法练
1.答案 5
解析 利用χ2的计算公式,建立关于m的方程.
χ2=(m>0),化简,得m2+70m-375=0(m>0),
所以m=5.
2.答案 57
解析 因为有99%的把握认为热爱数学与学生的年级有关,
所以χ2=>6.635,
构造函数,通过求导得到函数的单调性,进而求解,体现了函数思想.
令f(m)=(50+m)[30(m-20)-400]2-6.635×50×m×50×m,则f(m)>0,
易得f '(m)=25(108m2-2 527m-80 000),
因为函数y=25(108m2-2 527m-80 000)的图象的对称轴为直线m=<50,且当m=50时,y>0,
所以f '(m)=25(108m2-2 527m-80 000)在[50,+∞)上恒大于0,
所以f(m)在[50,+∞)上单调递增,
而f(56)<0,f(57)>0,m∈N*,
所以实数m的最小值为57.
3.C 由题中统计图可知2013~2017年,y随着x的增加平缓下降,2018~2022年,y随着x的增加迅速下降,
根据题图可直观得出污染天数y与年份x在每个阶段的关系,体现了数形结合的思想.
根据经验回归方程的几何意义可知,<0,由点的分布可知,∈(∈(),所以.
故选C.
4.解析 (1)根据题中的散点图,选择合适的回归方程模型,体现了数形结合思想.
根据题中的散点图判断,y=c1更适宜作为y与x之间的回归方程模型.
由题知,z=ln y,则z=c2x+ln c1,∴,ln ,
所以y关于x的回归方程为.
(2)由题意,设随机挑选一批,取出2个鱼卵,其中死卵个数为ξ,则ξ的可能取值为0,1,2,
设事件Ai=“所取2个鱼卵来自第i批”(i=1,2),则P(A1)=P(A2)=,
设事件Bj=“所取2个鱼卵有j个死卵”(j=0,1,2),
由全概率公式得,
P(ξ=0)=P(A1)P(B0|A1)+P(A2)P(B0|A2)=,
P(ξ=1)=P(A1)P(B1|A1)+P(A2)P(B1|A2)=,
P(ξ=2)=P(A1)P(B2|A1)+P(A2)P(B2|A2)=,
所以ξ的概率分布为
ξ 0 1 2
P
所以E(ξ)=0×.
思想方法 数形结合包括两个方面:一是“以数解形”,二是“以形助数”.本章数形结合思想主要体现在通过散点图来刻画相关关系,从而确定并求解回归模型.
5.解析 (1)通过换元,将y=aebx转化为经验回归方程,进而利用公式求解,体现了转化与化归的思想.
由y=aebx,得ln y=ln a+bx,
由题知,u=ln y,则u=ln a+bx,
由已知,得≈4.78,=12+22+32+42+52+62=91,
∴=0.324,
ln =4.78-0.324×3.5=3.646,
∴ln =3.646+0.324x,
∴=e0.324x+3.646.
(2)记“甲最终赢得比赛”为事件A,则事件A包含三种情况:
①接下去进行两局比赛,甲都赢了;
②接下去进行三局比赛,乙在前两局胜了其中一局,甲赢了剩余两局;
③接下去进行四局比赛,乙在前三局胜了其中两局,甲赢了剩余两局.
故P(A)=,
所以甲最终赢得比赛的概率为.
6.解析 (1)由题可得=55,
则=1.2,
=2.2-1.2×3=-1.4,
所以=1.2t-1.4.
(2)将t=x-2 012,z=y-5,代入=1.2t-1.4,
得-5=1.2(x-2 012)-1.4,即=1.2x-2 410.8.
通过换元,将z关于t的经验回归方程转化为y关于x的经验回归方程,体现了转化与化归的思想.
(3)当x=2 024时,=1.2×2 024-2 410.8=18,
所以预测到2024年年底,此银行储蓄存款可达18千亿元.
思想方法 转化与化归思想在回归分析中的应用主要有:(1)在求经验回归方程时,如果x,y的值很大,直接求解较为烦琐,此时可以将数据xi,yi(i=1,2,…,n)分别减去m,k,得xi-m,yi-k(i=1,2,…,n),利用处理后的新数据,按照求经验回归方程的步骤求出;(2)将非线性回归问题转化为线性回归问题进行分析,使之得到解决.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025苏教版高中数学选择性必修第二册
本章复习提升
易混易错练
易错点1 选错回归模型致错
1.(2024江苏常州高级中学期末)某公司为了了解年研发资金投入金额x(单位:亿元)对年销售额y(单位:亿元)的影响,对公司近12年的年研发资金投入金额和年销售额的数据进行了对比分析,建立了两个模型:①y=α+βx2,②y=eλx+t,其中α,β,λ,t均为常数,e为自然对数的底数,并得到一些统计量的值.令ui=,vi=ln yi,i=1,2,3,…,12,经计算得如下数据:
)2 )2
22 66 77 2
)2 )2
460 5 31 250 3.08
) )
220 14
(1)请从样本相关系数的角度,分析哪一个模型拟合效果更好;
(2)根据(1)中分析及表中数据,求y关于x的回归方程.
附:样本相关系数r=;经验回归方程x中,.
2.某农科所发现,一种作物的年收获量s(单位:kg)与“相近”作物株数n具有相关关系(两株作物“相近”是指它们的直线距离不超过1 m),并分别记录了“相近”作物株数为1,2,3,5,6,7时,该作物的年收获量的相关数据如下表:
n 1 2 3 5 6 7
s 60 55 53 46 45 41
(1)根据研究发现,该作物的年收获量s和“相近”作物株数n有以下两种可能的回归方程:①;②.利用统计知识,结合样本相关系数r比较使用哪种回归方程更合适;
(2)如图所示,农科所在正方形地块的每个格点(指横、纵直线的交叉点)处都种了一株该作物,其中每个小正方形的面积为1 m2,若在所种作物中随机选取一株,求它的年收获量的概率分布与数学期望.(注:年收获量以(1)中选择的回归方程计算所得数据为依据)
参考公式:经验回归方程为,其中,样本相关系数r=.
参考数据:≈2.65,≈43,其中wi=.
易错点2 用错公式致错
3.(2024江苏淮安马坝高级中学学情调研)某商场统计了2022年1月~5月某商品的线上月销售量y(单位:千件)与售价x(单位:元/件)的情况如下表所示.
月份 1 2 3 4 5
售价x/ (元/件) 60 56 58 57 54
月销售量 y/千件 5 9 7 10 9
(1)求样本相关系数r,并说明是否可以用线性回归模型拟合y与x的关系(当|r|∈[0.75,1]时,可以认为两个变量有很强的线性相关性;否则,没有很强的线性相关性.结果精确到0.01);
(2)建立y关于x的经验回归方程,并估计当售价为55元/件时,该商品的线上月销售量为多少千件;
(3)若每件商品的进价为(0.5x+25)元,不考虑其他费用,由(2)中结论,当商品售价为多少时,可使得该商品的月利润最大 (结果保留整数)
4.(2023江苏扬州中学期中)为了检测某种抗病毒疫苗的免疫效果,需要进行动物与人体试验.研究人员将疫苗注射到200只小白鼠体内,一段时间后测量小白鼠的某项指标值,按[0,20),[20,40),[40,60),[60,80),[80,100]分组,绘制频率直方图如图所示,试验发现小白鼠体内产生抗体的有160只,其中该项指标值不小于60的有110只,假设小白鼠每次注射疫苗后是否产生抗体相互独立.
(1)填写下面的2×2列联表,并根据列联表及独立性检验,判断能否认为注射疫苗后小白鼠产生抗体与指标值不小于60有关;
指标值 合计
小于60 不小于60
有抗体
没有抗体
合计
(2)为检验疫苗二次接种的免疫抗体性,对第一次注射疫苗后没有产生抗体的40只小白鼠进行第二次疫苗注射,结果又有20只小白鼠产生抗体.
①用频率估计概率,求一只小白鼠注射2次疫苗后产生抗体的概率p;
②以①中确定的概率p作为人体注射2次疫苗后产生抗体的概率,进行人体接种试验,记n个人注射2次疫苗后产生抗体的人数为X.试验后统计数据显示,当X=99时,P(X)取最大值,求参加人体接种试验的人数n.
参考公式: χ2=,其中n=a+b+c+d.
参考数据:
P(χ2≥x0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025
x0 0.455 0.708 1.323 2.072 2.706 3.841 5.024
思想方法练
一、函数与方程思想在独立性检验中的应用
1.(2024辽宁朝阳建平实验中学)已知2×2列联表如下:
温度低 于30 ℃ 温度不低 于30 ℃ 合计
高产量 15 m 15+m
低产量 5 15 20
合计 20 15+m 35+m
若χ2=(m>0),则m= .
附: χ2=,其中n=a+b+c+d.
2.(2024湖南大联考模拟)某市教育局为了调查学生热爱数学是否与学生的年级有关,从全市随机抽取了50名高二学生和m(m>50)名高三学生进行调查,每名学生对“是否热爱数学”提出“热爱”或“不热爱”的观点,得到如下数据:
观点 高二 高三
热爱 30 20
不热爱 20
若有99%的把握认为热爱数学与学生的年级有关,则实数m的最小值为 .
附: χ2=,其中n=a+b+c+d.
P(χ2≥x0) 0.050 0.010 0.001
x0 3.841 6.635 10.828
二、数形结合思想在回归分析中的应用
3.下图是某地区2013年至2022年污染天数y与年份x的折线图,根据2013~2017年的数据,2018~2022年的数据,2013~2022年的数据分别得到经验回归方程,则( )
A. B.
C. D.
4.(2023江苏镇江中学三模)经观测,长江中某些鱼类的产卵数y与温度x有关,现将收集到的温度xi和产卵数yi(i=1,2,…,10)的10组观测数据做了初步处理,得到如下散点图及统计量.
xi ti yi zi
360 54.5 1 360 44
)2 )2 )
384 3 588
) )
32 6 430
表中ti=,zi=ln yi,zi.
(1)根据散点图判断,y=a+bx(a,b为常数),y=n+m(x≥0,n,m为常数)与y=c1(c1,c2为常数,且c1>0,c2≠0)哪一个适宜作为y与x之间的回归方程模型,并求出y关于x的回归方程;(给出判断即可,不必说明理由)
(2)某兴趣小组抽取两批鱼卵,已知第一批中共有6个鱼卵,其中死卵有2个;第二批中共有8个鱼卵,其中死卵有3个.现随机挑选一批,然后从该批次中随机取出2个鱼卵,求取出死卵个数的概率分布及数学期望.
附:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其经验回归直线u的斜率和截距的最小二乘估计分别为.
、转化与化归思想在回归分析中的应用
5.(2024江苏南通适应性考试)随着科技的发展,手机的功能已经非常强大,各类App让用户的生活质量得到极大的提升,但是大量的青少年却沉迷于手机游戏,极大地毒害了青少年的身心健康.为了引导青少年抵制不良游戏,适度参与益脑游戏,某游戏公司开发了一款益脑游戏App,在内测时收集了玩家对每一关的平均过关时间,如下表:
关卡x 1 2 3 4 5 6
平均过关 时间y/秒 50 78 124 121 137 352
(1)通过分析,可用模型y=aebx拟合y与x的关系,试求y与x的回归方程;
(2)甲和乙约定举行对战赛,每局比赛通关用时少的人获胜(假设甲、乙都能通关),两人约定先胜4局者赢得比赛.已知甲每局获胜的概率为,乙每局获胜的概率为,若前3局中甲胜2局,乙胜1局,求甲最终赢得比赛的概率.
参考公式:对于一组数据(xi,yi)(i=1,2,3,…,n),其经验回归直线.
参考数据:ui≈28.67,xiui≈106.05,其中ui=ln yi.
6.(2024山东潍坊临朐第一中学月考)某地随着经济的发展,居民收入逐年增长,该地一银行连续五年的储蓄存款(年底余额)数据如表1:
年份x 2013 2014 2015 2016 2017
储蓄存款 y/千亿元 5 6 7 8 10
为了研究计算的方便,工作人员将表1的数据进行了处理,令t=x-2 012,z=y-5,得到表2:
时间代号t 1 2 3 4 5
z 0 1 2 3 5
(1)求z关于t的经验回归方程;
(2)通过(1)中的方程,求出y关于x的经验回归方程;
(3)用所求经验回归方程预测到2024年年底,此银行储蓄存款可达多少.
附:对于经验回归方程.
答案与分层梯度式解析
本章复习提升
易混易错练
1.解析 (1)设模型①和②的样本相关系数分别为r1,r2.
由题意可得,r1==0.88,
r2=≈0.91,
所以|r1|<|r2|,由样本相关系数的性质可得,模型②的拟合效果更好.
(2)因为y=eλx+t,所以ln y=λx+t,
由题知,v=ln y,则v=λx+t,
可得×22=1,
所以v关于x的经验回归方程为x+1,
即y关于x的回归方程为.
2.解析 (1)×(60+55+53+46+45+41)=50,
则)=(-3)×10+(-2)×5+(-1)×3+1×(-4)+2×(-5)+3×(-9)=-84,
)2=(-3)2+(-2)2+(-1)2+12+22+32=28,
)2=102+52+32+(-4)2+(-5)2+(-9)2=256,
设回归方程①和②的样本相关系数分别为r1,r2,则r1=≈-0.991,
令w=n2,则r2≈≈-0.965,
∴|r1|>|r2|,
∴回归方程①更合适.
(2)由(1)知=50+3×4=62,
故所求的经验回归方程为=-3n+62,
结合题中图形可知n的可能取值为2,3,4,代入经验回归方程中可求得与之相对应的s的估计值分别为56,53,50,
则P(s=56)=P(n=2)=,
P(s=53)=P(n=3)=,
P(s=50)=P(n=4)=.
∴年收获量s的概率分布为
s 56 53 50
P
∴E(s)=56×=53.
易错警示 本题易出错的地方有两点:①对样本相关系数的含义理解不准确,选错回归方程致错;②对经验回归方程的含义理解不准确,在解决第(2)问时没有利用第(1)问中的经验回归方程进行估计,而是利用了题表中的数据.
3.解析 (1)由题表中的数据,得=8,
则,
=4,
)=3×(-3)+(-1)×1+1×(-1)+0×2+(-3)×1=-14,
所以r=≈-0.78,
因为|r|>0.75,所以y与x有很强的线性相关性,可以用线性回归模型拟合.
(2)设经验回归方程为=-0.7,
=8-(-0.7)×57=47.9,
所以y关于x的经验回归方程为=-0.7x+47.9,
当x=55时,=-0.7×55+47.9=9.4,
故当售价为55元/件时,该商品的线上月销售量约为9.4千件.
(3)设该商品的月利润为Z元,则Z=1 000(x-0.5x-25)×(-0.7x+47.9)=50(-7x2+829x-23 950),
当x=≈59时,Z取得最大值.
即当商品售价为59元/件时,可使得该商品的月利润最大.
4.解析 (1)由题中的频率直方图,知200只小白鼠按指标值分布如下:
在[0,20)内的有0.002 5×20×200=10(只);
在[20,40)内的有0.006 25×20×200=25(只);
在[40,60)内的有0.008 75×20×200=35(只);
在[60,80)内的有0.025×20×200=100(只);
在[80,100]内的有0.007 5×20×200=30(只).
由题意知有抗体且指标值小于60的有50只,
而指标值小于60的小白鼠共有10+25+35=70(只),
所以指标值小于60且没有抗体的小白鼠有20只,
同理,指标值不小于60且没有抗体的小白鼠有20只,
故2×2列联表如下:
指标值 合计
小于60 不小于60
有抗体 50 110 160
没有抗体 20 20 40
合计 70 130 200
提出假设H0:注射疫苗后小白鼠产生抗体与指标值不小于60无关.
根据列联表中的数据,得χ2=≈4.945,
因为当H0成立时, χ2≥3.841的概率约为0.05,
所以我们有95%的把握认为,注射疫苗后小白鼠产生抗体与指标值不小于60有关.
(2)①设事件A=“小白鼠第一次注射疫苗后产生抗体”,事件B=“小白鼠第二次注射疫苗后产生抗体”,事件C=“小白鼠注射2次疫苗后产生抗体”,
则P(A)==0.5,
P(C)=P(A)+P()P(B)=0.8+0.2×0.5=0.9,
所以一只小白鼠注射2次疫苗后产生抗体的概率p=0.9.
②由题意,知随机变量X~B(n,0.9),
P(X=k)=×0.9k×0.1n-k(k=0,1,2,…,n),
因为P(X=99)最大,
所以
解得109≤n≤110,
因为n是整数,所以n=109或n=110,
所以参加人体接种试验的人数n为109或110.
易错警示 先根据题意准确写出2×2列联表,然后利用公式求出χ2的值,最后根据χ2的估计值选择临界值表中的对应数据进行比较.注意χ2的计算公式中,a,b,c,d的各项要准确对应,不要弄混.
思想方法练
1.答案 5
解析 利用χ2的计算公式,建立关于m的方程.
χ2=(m>0),化简,得m2+70m-375=0(m>0),
所以m=5.
2.答案 57
解析 因为有99%的把握认为热爱数学与学生的年级有关,
所以χ2=>6.635,
构造函数,通过求导得到函数的单调性,进而求解,体现了函数思想.
令f(m)=(50+m)[30(m-20)-400]2-6.635×50×m×50×m,则f(m)>0,
易得f '(m)=25(108m2-2 527m-80 000),
因为函数y=25(108m2-2 527m-80 000)的图象的对称轴为直线m=<50,且当m=50时,y>0,
所以f '(m)=25(108m2-2 527m-80 000)在[50,+∞)上恒大于0,
所以f(m)在[50,+∞)上单调递增,
而f(56)<0,f(57)>0,m∈N*,
所以实数m的最小值为57.
3.C 由题中统计图可知2013~2017年,y随着x的增加平缓下降,2018~2022年,y随着x的增加迅速下降,
根据题图可直观得出污染天数y与年份x在每个阶段的关系,体现了数形结合的思想.
根据经验回归方程的几何意义可知,<0,由点的分布可知,∈(∈(),所以.
故选C.
4.解析 (1)根据题中的散点图,选择合适的回归方程模型,体现了数形结合思想.
根据题中的散点图判断,y=c1更适宜作为y与x之间的回归方程模型.
由题知,z=ln y,则z=c2x+ln c1,∴,ln ,
所以y关于x的回归方程为.
(2)由题意,设随机挑选一批,取出2个鱼卵,其中死卵个数为ξ,则ξ的可能取值为0,1,2,
设事件Ai=“所取2个鱼卵来自第i批”(i=1,2),则P(A1)=P(A2)=,
设事件Bj=“所取2个鱼卵有j个死卵”(j=0,1,2),
由全概率公式得,
P(ξ=0)=P(A1)P(B0|A1)+P(A2)P(B0|A2)=,
P(ξ=1)=P(A1)P(B1|A1)+P(A2)P(B1|A2)=,
P(ξ=2)=P(A1)P(B2|A1)+P(A2)P(B2|A2)=,
所以ξ的概率分布为
ξ 0 1 2
P
所以E(ξ)=0×.
思想方法 数形结合包括两个方面:一是“以数解形”,二是“以形助数”.本章数形结合思想主要体现在通过散点图来刻画相关关系,从而确定并求解回归模型.
5.解析 (1)通过换元,将y=aebx转化为经验回归方程,进而利用公式求解,体现了转化与化归的思想.
由y=aebx,得ln y=ln a+bx,
由题知,u=ln y,则u=ln a+bx,
由已知,得≈4.78,=12+22+32+42+52+62=91,
∴=0.324,
ln =4.78-0.324×3.5=3.646,
∴ln =3.646+0.324x,
∴=e0.324x+3.646.
(2)记“甲最终赢得比赛”为事件A,则事件A包含三种情况:
①接下去进行两局比赛,甲都赢了;
②接下去进行三局比赛,乙在前两局胜了其中一局,甲赢了剩余两局;
③接下去进行四局比赛,乙在前三局胜了其中两局,甲赢了剩余两局.
故P(A)=,
所以甲最终赢得比赛的概率为.
6.解析 (1)由题可得=55,
则=1.2,
=2.2-1.2×3=-1.4,
所以=1.2t-1.4.
(2)将t=x-2 012,z=y-5,代入=1.2t-1.4,
得-5=1.2(x-2 012)-1.4,即=1.2x-2 410.8.
通过换元,将z关于t的经验回归方程转化为y关于x的经验回归方程,体现了转化与化归的思想.
(3)当x=2 024时,=1.2×2 024-2 410.8=18,
所以预测到2024年年底,此银行储蓄存款可达18千亿元.
思想方法 转化与化归思想在回归分析中的应用主要有:(1)在求经验回归方程时,如果x,y的值很大,直接求解较为烦琐,此时可以将数据xi,yi(i=1,2,…,n)分别减去m,k,得xi-m,yi-k(i=1,2,…,n),利用处理后的新数据,按照求经验回归方程的步骤求出;(2)将非线性回归问题转化为线性回归问题进行分析,使之得到解决.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
