广东省江门市新会一中2024-2025学年高二上学期期中数学试卷(PDF版,含答案)
文档属性
| 名称 | 广东省江门市新会一中2024-2025学年高二上学期期中数学试卷(PDF版,含答案) |

|
|
| 格式 | |||
| 文件大小 | 653.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-13 14:15:23 | ||
图片预览




文档简介
广东省江门市新会一中 2024-2025 学年高二上学期期中数学试卷
一、单选题:本题共 8 小题,每小题 5 分,共 40 分。在每小题给出的选项中,只有一项是符合题目要求的。
1.在简单随机抽样中,某一个个体被抽中的可能性( )
A. 与第几次抽样有关,第1次抽中的可能性要大些
B. 与第几次抽样无关,每次抽中的可能性都相等
C. 与第几次抽样有关,最后一次抽中的可能性大些
D. 与第几次抽样无关,每次都是等可能的抽取,但各次抽取的可能性不一样
2.某烟花爆竹厂从20万件同类产品中随机抽取了100件进行质检,发现其中有5件不合格,那么请你估计该
厂这20万件产品中不合格产品约有( )
A. 1万件 B. 18万件 C. 19万件 D. 20万件
3.若直线√ 3 + +1 = 0的倾斜角为 ,在 轴上的截距为 ,则( )
5 2
A. = , = 1 B. = , = 1
6 3
2 5
C. = , = 1 D. = , = 1
3 6
4.如图所示,在平行六面体 1 1 1 1中, 为 1 1与 1 1的交点.若 = , = , 1 = ,
则下列向量中与 相等的向量是( )
1 1 1 1
A. + + B. + +
2 2 2 2
1 1 1 1
C. + D. +
2 2 2 2
5.给定组数5,4,3,5,3,2,2,3,1,2,则错误的是( )
2√ 10
A. 中位数为3 B. 标准差为 C. 众数为2和3 D. 第85百分位数为4
5
6.已知向量 = ( , ), = (1, 2),从6张大小相同分别标有号码1,2,3,4,5,6的卡片中,有放回地抽取两张,
、 分别表示第一次、第二次抽取的卡片上的号码,则满足 > 0的概率是( )
第 1 页,共 10 页
1 3 1 1
A. B. C. D.
12 4 5 6
+1
7.设 ( 2,3), (1,2),若点 ( , )在线段 上,则 的取值范围是( )
A. [ 2,3] B. ( 2,3)
C. ( ∞, 2]∪[3,+∞) D. ( ∞, 2) ∪ (3,+∞)
8.在空间直角坐标系 中, (1,1,1), (0,1,0), (0,0,1),点 在平面 内,则当点 与 间的距离取
最小值时,点 的坐标是( )
2 1 1 2 1 1 1 1 1 1 1 1
A. ( , , ) B. ( , , ) C. ( , , ) D. ( , , )
3 3 3 3 3 3 3 3 3 3 3 3
二、多选题:本题共 3 小题,共 18 分。在每小题给出的选项中,有多项符合题目要求。
9.如图所示,下列频率分布直方图显示了三种不同的分布形态.图(1)形成对称形态,图(2)形成“右拖尾”
形态,图(3)形成“左拖尾”形态,根据所给图象作出以下判断,正确的是( )
A. 图(1)的平均数=中位数=众数 B. 图(2)的众数<平均数<中位数
C. 图(2)的众数<中位数<平均数 D. 图(3)的中位数<平均数<众数
10.下列事件中, , 是相互独立事件的是( )
A. 一枚硬币掷两次, =“第一次为正面”, =“第二次为反面”
B. 袋中有2个白球,2个黑球,不放回地摸两球, =“第一次摸到白球”, =“第二次摸到白球”
C. 掷一枚骰子, =“出现点数为奇数”, =“出现点数为3或4”
D. 掷一枚骰子, =“出现点数为奇数”, =“出现点数为偶数”
11.如图,在棱长为2的正方体 1 1 1 1中, 为线段 1 上的动点,则( )
第 2 页,共 10 页
2√ 14
A. 当 1 = 2 时, = 3
B. 直线 1 与 所成的角不可能是 6
1 √ 3
C. 若 1 = 1 ,则二面角 3 1 1平面角的正弦值为 6
2
D. 当 1 = 2 时,点 1到平面 1 的距离为 3
三、填空题:本题共 3 小题,每小题 5 分,共 15 分。
12.经过 (0,2), ( 1,0)两点的直线的方向向量为(1, ),则实数 的值为______.
13.如图,在平行六面体 1 1 1 1中,| | = 2,| | = 3,| 1 | = 4,
∠ = 90°,∠ 1 = ∠ 1 = 60°,则| 1 | = ______.
14.由1,2,3,…,1000这个1000正整数构成集合 ,先从集合 中随机取一个数 ,取出后把 放回集合 ,
1
然后再从集合 中随机取出一个数 ,则 > 的概率为 .
3
四、解答题:本题共 5 小题,共 60 分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题12分)
已知 的顶点分别为 (2,4), (7, 1), ( 6,1).
(1)求 边的中线 所在直线的方程;
(2)求 边的垂直平分线 的方程.
16.(本小题12分)
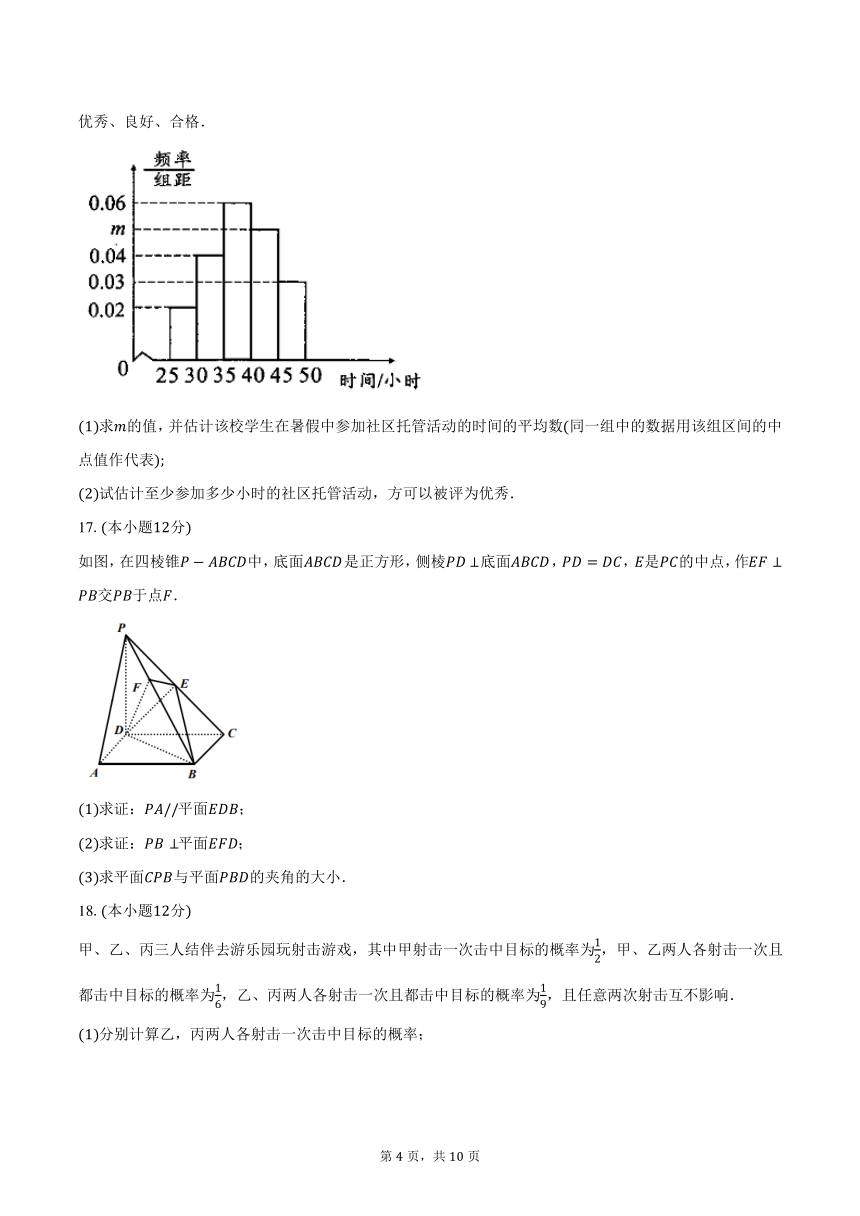
为鼓励青年大学生积极参与暑期社会实践,某高校今年暑假组织返乡大学生积极参与了当地的暑假社区儿
童托管服务.现抽样调查了其中100名大学生,统计他们参加社区托管活动的时间(单位:小时),并将统计数
据制成如图所示的频率分布直方图.另外,根据参加社区托管活动的时间从长到短按3: 4:3的比例分别被评为
第 3 页,共 10 页
优秀、良好、合格.
(1)求 的值,并估计该校学生在暑假中参加社区托管活动的时间的平均数(同一组中的数据用该组区间的中
点值作代表);
(2)试估计至少参加多少小时的社区托管活动,方可以被评为优秀.
17.(本小题12分)
如图,在四棱锥 中,底面 是正方形,侧棱 ⊥底面 , = , 是 的中点,作 ⊥
交 于点 .
(1)求证: //平面 ;
(2)求证: ⊥平面 ;
(3)求平面 与平面 的夹角的大小.
18.(本小题12分)
1
甲、乙、丙三人结伴去游乐园玩射击游戏,其中甲射击一次击中目标的概率为 ,甲、乙两人各射击一次且
2
1 1
都击中目标的概率为 ,乙、丙两人各射击一次且都击中目标的概率为 ,且任意两次射击互不影响.
6 9
(1)分别计算乙,丙两人各射击一次击中目标的概率;
第 4 页,共 10 页
(2)求甲、乙、丙各射击一次恰有一人击中目标的概率;
99
(3)若乙想击中目标的概率不低于 ,乙至少需要射击多少次?(参考数据: 2 ≈ 0.3010, 3 ≈ 0.4771)
100
19.(本小题12分)
在空间直角坐标系 中,已知向量 = ( , , ),点 0 ( 0, 0 , 0).若直线 以 为方向向量且经过点 0,
则直线 的标准式方程可表示为 0 = 0 = 0 ( ≠ 0);若平面 以 为法向量且经过点 0,则平面 的
点法式方程表示为 ( 0)+ ( 0) + ( 0)= 0.
1 2 +1
(1)已知直线 的标准式方程为 = = ,平面 1的点法式方程可表示为√ 3 + + 5 = 0,求直1 √ 3 1
线 与平面 1所成角的余弦值;
(2)已知平面 2的点法式方程可表示为2 + 3 + 1 = 0,平面外一点 (1,2,1),求点 到平面 2的距离;
(3)( )若集合 = {( , , )|| | + | | ≤ 2,| | ≤ 1},记集合 中所有点构成的几何体为 ,求几何体 的体积:
( )若集合 = {( , , )|| | + | | ≤ 2,| | + | | ≤ 2,| | + | | ≤ 2}.记集合 中所有点构成的几何体为 ,求
几何体 相邻两个面(有公共棱)所成二面角的大小
第 5 页,共 10 页
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】2
13.【答案】7
1667
14.【答案】
2000
15.【答案】(1)设 中点 的坐标为( 0, 0),
7 6 1 1+1
则 0 = = , 0 = = 0, 2 2 2
1
∵ 边的中线 过点 (2,4), ( , 0)两点,
2
4 0 1
∴ 所在直线方程为 0 = 1 ( ),即8 3 4 = 0;
2 2
2
1 1 2
(2) ∵ 的斜率 = = ,
7+6 13
13
∴ 的垂直平分线 的斜率 1 = , 2
13 ( 1∴直线 的方程为 0 = ),即26 4 13 = 0.
2 2
16.【答案】解:(1)由题意得,(0.02+ 0.03+ 0.04+ +0.06)× 5 = 1,解得 = 0.05.
因为(0.02× 27.5+ 0.04× 32.5 + 0.06× 37.5 + 0.05 × 42.5+ 0.03 × 47.5)× 5 = 38.25,
所以可以估计该校学生在暑假中参加社区托管活动的时间的平均数约为38.25小时.
(2)由题意得,因为0.03 × 5 = 0.15,(0.03+ 0.05) × 5 = 0.4,
第 6 页,共 10 页
那么第70百分位数位于40 45之间.
设第70百分位数为 ,则(45 ) × 0.05 = 0.15,解得 = 42.
故至少参加42小时的社会实践活动,方可被评为优秀.
17.【答案】(1)证明:因为 ⊥底面 , , 底面 ,
所以 ⊥ , ⊥ ,
又底面 是正方形,所以 ⊥ ,
以 为原点, , , 所在直线分别为 轴, 轴, 轴,建立空间直角坐标系,
设 = 1.
1 1
依题意得 (1,0,0), (1,1,0), (0,0,1), (0, , ).
2 2
( 1 1所以 = 1,0, 1), = (1,1,0), = (0, , ).
2 2
设平面 的一个法向量为 = ( 1, 1 , 1),
= 1 + 1 = 0,
则有{
1 1
= +
2 1 2 1
= 0,
= ,
即{ 1 1 = ,取 = (1, 1,1),则
= 0,
1 1
因为 平面 ,因此 //平面 .
(2)证明:依题意得 = (1,1, 1),
1 1
因为 = 0 + = 0,
2 2
所以 ⊥ .
由已知 ⊥ ,且 ∩ = , , 平面 ,
所以 ⊥平面 .
第 7 页,共 10 页
(3)解:依题意得 (0,1,0),且 = (1,0,0), = (0,1, 1).
设平面 的一个法向量为 = ( 2 , 2 , 2),
= = 0,
则{ 2
= 2 2 = 0,
= 0,
即{ 2 ( ) 2 = 2 ,
,取 = 0,1,1 .
易知平面 的一个法向量为 = (1, 1,0),
1
所以cos , = = . | || | 2
所以平面 与平面 的夹角为 .
3
1
18.【答案】解:甲、乙、丙三人结伴去游乐园玩射击游戏,其中甲射击一次击中目标的概率为 ,甲、乙两
2
1 1
人各射击一次且都击中目标的概率为 ,乙、丙两人各射击一次且都击中目标的概率为 ,
6 9
(1)记乙射击一次击中目标为事件 ,丙射击一次击中目标为事件 ,甲射击一次击中目标为事件 ,
1 1
依题意 ( ) = , ( ) = ( ) ( ) = ,
2 6
1
所以 ( ) = ,
3
1 1
( ) = ( ) ( ) = ,所以 ( ) = ,
9 3
1 1
所以丙射击一次击中目标的概率为 ,乙射击一次击中目标的概率为 ;
3 3
(2)记甲、乙、丙各射击一次恰有一人击中目标为事件 ,
则 ( ) = ( + + )
= ( ) + ( )+ ( )
1 2 2 1 1 2 1 2 1 4
= × × + × × + × × = ,
2 3 3 2 3 3 2 3 3 9
4
所以甲、乙、丙各射击一次恰有一人击中目标的概率 ;
9
2
(3)设乙射击 ( ∈ )次,则至少有一次击中目标的概率为1 [ ( )] = 1 ( ) ,
3
2 99 2 1
令1 ( ) ≥ ,所以( ) ≤ ,
3 100 3 100
1 100 2 2
所以 ≥ 2 = 3100 = 3 = ≈ ≈ 11.3571, 100
3 2 lg 3 2 0.4771 0.30102
又 为正整数,所以 = 12,即甲至少要射击12次.
第 8 页,共 10 页
19.【答案】解:(1)由题可知,直线 的一个方向向量坐标为 = (1, √ 3, 1),平面 1的一个法向量为 =
(√ 3, 1, 1),
1 1
设直线 与平面 1所成角为 ,则有 = | | = =| || | √ 5×√ 5 5
1 2√ 6
= √ 1 sin2 = √ 1 ( )2 = ,
5 5
直线 与平面 所成角的余弦值为2√ 61 . 5
(2)由题可知平面 2的法向量为 2 = (2,3,1),且过点 (0,0,1),
因为 (1,2,1),所以 = (1,2,0),
2
|2×1+3×2+1×0| 8 4√ 14
所以点 到平面 的距离为| | = = =2 | 2 | √ 14 7 . √ 22+32+1
(3)( )建立空间直角坐标系,
+ = 2, > 0, > 0
= 2, > 0, < 0
+ = 2, < 0, > 0
则 ,
= 2, < 0, < 0
= 1
{ = 1
如图:
然后得到几何体 为几何体 是底面边长为2√ 2的正方形,高为2的长方体,
故几何体 的体积为2√ 2 × 2√ 2 × 2 = 16,
( )由( )可知, = {( , , )|| | + | | ≤ 2,| | + | | ≤ 2,| | + | | ≤ 2}的图象是一个完全对称的图象,
所以我们只需讨论第一卦限的相邻两个平面的二面角即可,
第 9 页,共 10 页
此时 > 0, > 0, > 0,得 = {( , , )| + ≤ 2, + ≤ 2, + ≤ 2, > 0, > 0, > 0},画
出第一卦限图象,显然其二面角为钝角,
计算平面 + = 2, + = 2的二面角,
所以两个平面的法向量分别为 2 = (1,1,0), 3 = (0,1,1),
设二面角的大小为 ,
2 3 |0+1+0| 1
则 = | | = = , || 2 || 3 | √ 1+1×√ 1+1 2
2
所以二面角的大小为 .
3
第 10 页,共 10 页
一、单选题:本题共 8 小题,每小题 5 分,共 40 分。在每小题给出的选项中,只有一项是符合题目要求的。
1.在简单随机抽样中,某一个个体被抽中的可能性( )
A. 与第几次抽样有关,第1次抽中的可能性要大些
B. 与第几次抽样无关,每次抽中的可能性都相等
C. 与第几次抽样有关,最后一次抽中的可能性大些
D. 与第几次抽样无关,每次都是等可能的抽取,但各次抽取的可能性不一样
2.某烟花爆竹厂从20万件同类产品中随机抽取了100件进行质检,发现其中有5件不合格,那么请你估计该
厂这20万件产品中不合格产品约有( )
A. 1万件 B. 18万件 C. 19万件 D. 20万件
3.若直线√ 3 + +1 = 0的倾斜角为 ,在 轴上的截距为 ,则( )
5 2
A. = , = 1 B. = , = 1
6 3
2 5
C. = , = 1 D. = , = 1
3 6
4.如图所示,在平行六面体 1 1 1 1中, 为 1 1与 1 1的交点.若 = , = , 1 = ,
则下列向量中与 相等的向量是( )
1 1 1 1
A. + + B. + +
2 2 2 2
1 1 1 1
C. + D. +
2 2 2 2
5.给定组数5,4,3,5,3,2,2,3,1,2,则错误的是( )
2√ 10
A. 中位数为3 B. 标准差为 C. 众数为2和3 D. 第85百分位数为4
5
6.已知向量 = ( , ), = (1, 2),从6张大小相同分别标有号码1,2,3,4,5,6的卡片中,有放回地抽取两张,
、 分别表示第一次、第二次抽取的卡片上的号码,则满足 > 0的概率是( )
第 1 页,共 10 页
1 3 1 1
A. B. C. D.
12 4 5 6
+1
7.设 ( 2,3), (1,2),若点 ( , )在线段 上,则 的取值范围是( )
A. [ 2,3] B. ( 2,3)
C. ( ∞, 2]∪[3,+∞) D. ( ∞, 2) ∪ (3,+∞)
8.在空间直角坐标系 中, (1,1,1), (0,1,0), (0,0,1),点 在平面 内,则当点 与 间的距离取
最小值时,点 的坐标是( )
2 1 1 2 1 1 1 1 1 1 1 1
A. ( , , ) B. ( , , ) C. ( , , ) D. ( , , )
3 3 3 3 3 3 3 3 3 3 3 3
二、多选题:本题共 3 小题,共 18 分。在每小题给出的选项中,有多项符合题目要求。
9.如图所示,下列频率分布直方图显示了三种不同的分布形态.图(1)形成对称形态,图(2)形成“右拖尾”
形态,图(3)形成“左拖尾”形态,根据所给图象作出以下判断,正确的是( )
A. 图(1)的平均数=中位数=众数 B. 图(2)的众数<平均数<中位数
C. 图(2)的众数<中位数<平均数 D. 图(3)的中位数<平均数<众数
10.下列事件中, , 是相互独立事件的是( )
A. 一枚硬币掷两次, =“第一次为正面”, =“第二次为反面”
B. 袋中有2个白球,2个黑球,不放回地摸两球, =“第一次摸到白球”, =“第二次摸到白球”
C. 掷一枚骰子, =“出现点数为奇数”, =“出现点数为3或4”
D. 掷一枚骰子, =“出现点数为奇数”, =“出现点数为偶数”
11.如图,在棱长为2的正方体 1 1 1 1中, 为线段 1 上的动点,则( )
第 2 页,共 10 页
2√ 14
A. 当 1 = 2 时, = 3
B. 直线 1 与 所成的角不可能是 6
1 √ 3
C. 若 1 = 1 ,则二面角 3 1 1平面角的正弦值为 6
2
D. 当 1 = 2 时,点 1到平面 1 的距离为 3
三、填空题:本题共 3 小题,每小题 5 分,共 15 分。
12.经过 (0,2), ( 1,0)两点的直线的方向向量为(1, ),则实数 的值为______.
13.如图,在平行六面体 1 1 1 1中,| | = 2,| | = 3,| 1 | = 4,
∠ = 90°,∠ 1 = ∠ 1 = 60°,则| 1 | = ______.
14.由1,2,3,…,1000这个1000正整数构成集合 ,先从集合 中随机取一个数 ,取出后把 放回集合 ,
1
然后再从集合 中随机取出一个数 ,则 > 的概率为 .
3
四、解答题:本题共 5 小题,共 60 分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题12分)
已知 的顶点分别为 (2,4), (7, 1), ( 6,1).
(1)求 边的中线 所在直线的方程;
(2)求 边的垂直平分线 的方程.
16.(本小题12分)
为鼓励青年大学生积极参与暑期社会实践,某高校今年暑假组织返乡大学生积极参与了当地的暑假社区儿
童托管服务.现抽样调查了其中100名大学生,统计他们参加社区托管活动的时间(单位:小时),并将统计数
据制成如图所示的频率分布直方图.另外,根据参加社区托管活动的时间从长到短按3: 4:3的比例分别被评为
第 3 页,共 10 页
优秀、良好、合格.
(1)求 的值,并估计该校学生在暑假中参加社区托管活动的时间的平均数(同一组中的数据用该组区间的中
点值作代表);
(2)试估计至少参加多少小时的社区托管活动,方可以被评为优秀.
17.(本小题12分)
如图,在四棱锥 中,底面 是正方形,侧棱 ⊥底面 , = , 是 的中点,作 ⊥
交 于点 .
(1)求证: //平面 ;
(2)求证: ⊥平面 ;
(3)求平面 与平面 的夹角的大小.
18.(本小题12分)
1
甲、乙、丙三人结伴去游乐园玩射击游戏,其中甲射击一次击中目标的概率为 ,甲、乙两人各射击一次且
2
1 1
都击中目标的概率为 ,乙、丙两人各射击一次且都击中目标的概率为 ,且任意两次射击互不影响.
6 9
(1)分别计算乙,丙两人各射击一次击中目标的概率;
第 4 页,共 10 页
(2)求甲、乙、丙各射击一次恰有一人击中目标的概率;
99
(3)若乙想击中目标的概率不低于 ,乙至少需要射击多少次?(参考数据: 2 ≈ 0.3010, 3 ≈ 0.4771)
100
19.(本小题12分)
在空间直角坐标系 中,已知向量 = ( , , ),点 0 ( 0, 0 , 0).若直线 以 为方向向量且经过点 0,
则直线 的标准式方程可表示为 0 = 0 = 0 ( ≠ 0);若平面 以 为法向量且经过点 0,则平面 的
点法式方程表示为 ( 0)+ ( 0) + ( 0)= 0.
1 2 +1
(1)已知直线 的标准式方程为 = = ,平面 1的点法式方程可表示为√ 3 + + 5 = 0,求直1 √ 3 1
线 与平面 1所成角的余弦值;
(2)已知平面 2的点法式方程可表示为2 + 3 + 1 = 0,平面外一点 (1,2,1),求点 到平面 2的距离;
(3)( )若集合 = {( , , )|| | + | | ≤ 2,| | ≤ 1},记集合 中所有点构成的几何体为 ,求几何体 的体积:
( )若集合 = {( , , )|| | + | | ≤ 2,| | + | | ≤ 2,| | + | | ≤ 2}.记集合 中所有点构成的几何体为 ,求
几何体 相邻两个面(有公共棱)所成二面角的大小
第 5 页,共 10 页
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】2
13.【答案】7
1667
14.【答案】
2000
15.【答案】(1)设 中点 的坐标为( 0, 0),
7 6 1 1+1
则 0 = = , 0 = = 0, 2 2 2
1
∵ 边的中线 过点 (2,4), ( , 0)两点,
2
4 0 1
∴ 所在直线方程为 0 = 1 ( ),即8 3 4 = 0;
2 2
2
1 1 2
(2) ∵ 的斜率 = = ,
7+6 13
13
∴ 的垂直平分线 的斜率 1 = , 2
13 ( 1∴直线 的方程为 0 = ),即26 4 13 = 0.
2 2
16.【答案】解:(1)由题意得,(0.02+ 0.03+ 0.04+ +0.06)× 5 = 1,解得 = 0.05.
因为(0.02× 27.5+ 0.04× 32.5 + 0.06× 37.5 + 0.05 × 42.5+ 0.03 × 47.5)× 5 = 38.25,
所以可以估计该校学生在暑假中参加社区托管活动的时间的平均数约为38.25小时.
(2)由题意得,因为0.03 × 5 = 0.15,(0.03+ 0.05) × 5 = 0.4,
第 6 页,共 10 页
那么第70百分位数位于40 45之间.
设第70百分位数为 ,则(45 ) × 0.05 = 0.15,解得 = 42.
故至少参加42小时的社会实践活动,方可被评为优秀.
17.【答案】(1)证明:因为 ⊥底面 , , 底面 ,
所以 ⊥ , ⊥ ,
又底面 是正方形,所以 ⊥ ,
以 为原点, , , 所在直线分别为 轴, 轴, 轴,建立空间直角坐标系,
设 = 1.
1 1
依题意得 (1,0,0), (1,1,0), (0,0,1), (0, , ).
2 2
( 1 1所以 = 1,0, 1), = (1,1,0), = (0, , ).
2 2
设平面 的一个法向量为 = ( 1, 1 , 1),
= 1 + 1 = 0,
则有{
1 1
= +
2 1 2 1
= 0,
= ,
即{ 1 1 = ,取 = (1, 1,1),则
= 0,
1 1
因为 平面 ,因此 //平面 .
(2)证明:依题意得 = (1,1, 1),
1 1
因为 = 0 + = 0,
2 2
所以 ⊥ .
由已知 ⊥ ,且 ∩ = , , 平面 ,
所以 ⊥平面 .
第 7 页,共 10 页
(3)解:依题意得 (0,1,0),且 = (1,0,0), = (0,1, 1).
设平面 的一个法向量为 = ( 2 , 2 , 2),
= = 0,
则{ 2
= 2 2 = 0,
= 0,
即{ 2 ( ) 2 = 2 ,
,取 = 0,1,1 .
易知平面 的一个法向量为 = (1, 1,0),
1
所以cos , = = . | || | 2
所以平面 与平面 的夹角为 .
3
1
18.【答案】解:甲、乙、丙三人结伴去游乐园玩射击游戏,其中甲射击一次击中目标的概率为 ,甲、乙两
2
1 1
人各射击一次且都击中目标的概率为 ,乙、丙两人各射击一次且都击中目标的概率为 ,
6 9
(1)记乙射击一次击中目标为事件 ,丙射击一次击中目标为事件 ,甲射击一次击中目标为事件 ,
1 1
依题意 ( ) = , ( ) = ( ) ( ) = ,
2 6
1
所以 ( ) = ,
3
1 1
( ) = ( ) ( ) = ,所以 ( ) = ,
9 3
1 1
所以丙射击一次击中目标的概率为 ,乙射击一次击中目标的概率为 ;
3 3
(2)记甲、乙、丙各射击一次恰有一人击中目标为事件 ,
则 ( ) = ( + + )
= ( ) + ( )+ ( )
1 2 2 1 1 2 1 2 1 4
= × × + × × + × × = ,
2 3 3 2 3 3 2 3 3 9
4
所以甲、乙、丙各射击一次恰有一人击中目标的概率 ;
9
2
(3)设乙射击 ( ∈ )次,则至少有一次击中目标的概率为1 [ ( )] = 1 ( ) ,
3
2 99 2 1
令1 ( ) ≥ ,所以( ) ≤ ,
3 100 3 100
1 100 2 2
所以 ≥ 2 = 3100 = 3 = ≈ ≈ 11.3571, 100
3 2 lg 3 2 0.4771 0.30102
又 为正整数,所以 = 12,即甲至少要射击12次.
第 8 页,共 10 页
19.【答案】解:(1)由题可知,直线 的一个方向向量坐标为 = (1, √ 3, 1),平面 1的一个法向量为 =
(√ 3, 1, 1),
1 1
设直线 与平面 1所成角为 ,则有 = | | = =| || | √ 5×√ 5 5
1 2√ 6
= √ 1 sin2 = √ 1 ( )2 = ,
5 5
直线 与平面 所成角的余弦值为2√ 61 . 5
(2)由题可知平面 2的法向量为 2 = (2,3,1),且过点 (0,0,1),
因为 (1,2,1),所以 = (1,2,0),
2
|2×1+3×2+1×0| 8 4√ 14
所以点 到平面 的距离为| | = = =2 | 2 | √ 14 7 . √ 22+32+1
(3)( )建立空间直角坐标系,
+ = 2, > 0, > 0
= 2, > 0, < 0
+ = 2, < 0, > 0
则 ,
= 2, < 0, < 0
= 1
{ = 1
如图:
然后得到几何体 为几何体 是底面边长为2√ 2的正方形,高为2的长方体,
故几何体 的体积为2√ 2 × 2√ 2 × 2 = 16,
( )由( )可知, = {( , , )|| | + | | ≤ 2,| | + | | ≤ 2,| | + | | ≤ 2}的图象是一个完全对称的图象,
所以我们只需讨论第一卦限的相邻两个平面的二面角即可,
第 9 页,共 10 页
此时 > 0, > 0, > 0,得 = {( , , )| + ≤ 2, + ≤ 2, + ≤ 2, > 0, > 0, > 0},画
出第一卦限图象,显然其二面角为钝角,
计算平面 + = 2, + = 2的二面角,
所以两个平面的法向量分别为 2 = (1,1,0), 3 = (0,1,1),
设二面角的大小为 ,
2 3 |0+1+0| 1
则 = | | = = , || 2 || 3 | √ 1+1×√ 1+1 2
2
所以二面角的大小为 .
3
第 10 页,共 10 页
同课章节目录
