【期末专项复习】人教版数学八年级上册“全等三角形”综合检测题(含答案)
文档属性
| 名称 | 【期末专项复习】人教版数学八年级上册“全等三角形”综合检测题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 406.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-14 12:55:58 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【期末专项复习】人教版数学八年级上册“全等三角形”综合检测题
一、单选题
1.如图,BD=BC,BE=CA,∠DBE=∠C=62°,∠BDE=75°,则∠AFE的度数等于( )
A.148° B.140° C.135° D.128°
2.两个直角三角形中:①一锐角和斜边对应相等;②斜边一直角边对应相等;③有两条边相等;④两个锐角对应相等.其中能使这两个直角三角形全等的是( )
A.①② B.②③ C.①②③ D.①③④
3.如图,点C在的边上,尺规作图痕迹显示的是( )
A.作线段的垂直平分线 B.作的平分线
C.是等边三角形 D.作
4.已知图中的两个三角形全等,则等于( )
A. B. C. D.
5.如图,,,平分,则的大小为( )
A. B. C. D.
6.如图,在的长方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形.图中的为格点三角形,以点C为顶点的三角形最多能再画出( )个不同的格点三角形与全等.
A.8 B.9 C.10 D.11
7.如图,在中,,,平分,交于点,于点,且,则的周长为( )
A. B. C. D.不能确定
8.三条相互交叉的公路,现要建一个货物转运站,要求它到三条公路的距离相等,则可供选择的地址有( ).
A.1个 B.2个 C.3个 D.4个
9.一块三角形玻璃不小心打碎了,带上如图所示的玻璃碎片就能让玻璃店的师父重配一块与原来相同的三角形玻璃的依据是( )
A.SSS B.SAS C.AAS D.ASA
10.如图,AD是 的中线,E是AD上一点,连接BE并延长交AC于点F,若EF=AF,BE=7.5,CF=6,则EF=( ).
A.2.5 B.2 C.1.5 D.1
二、填空题
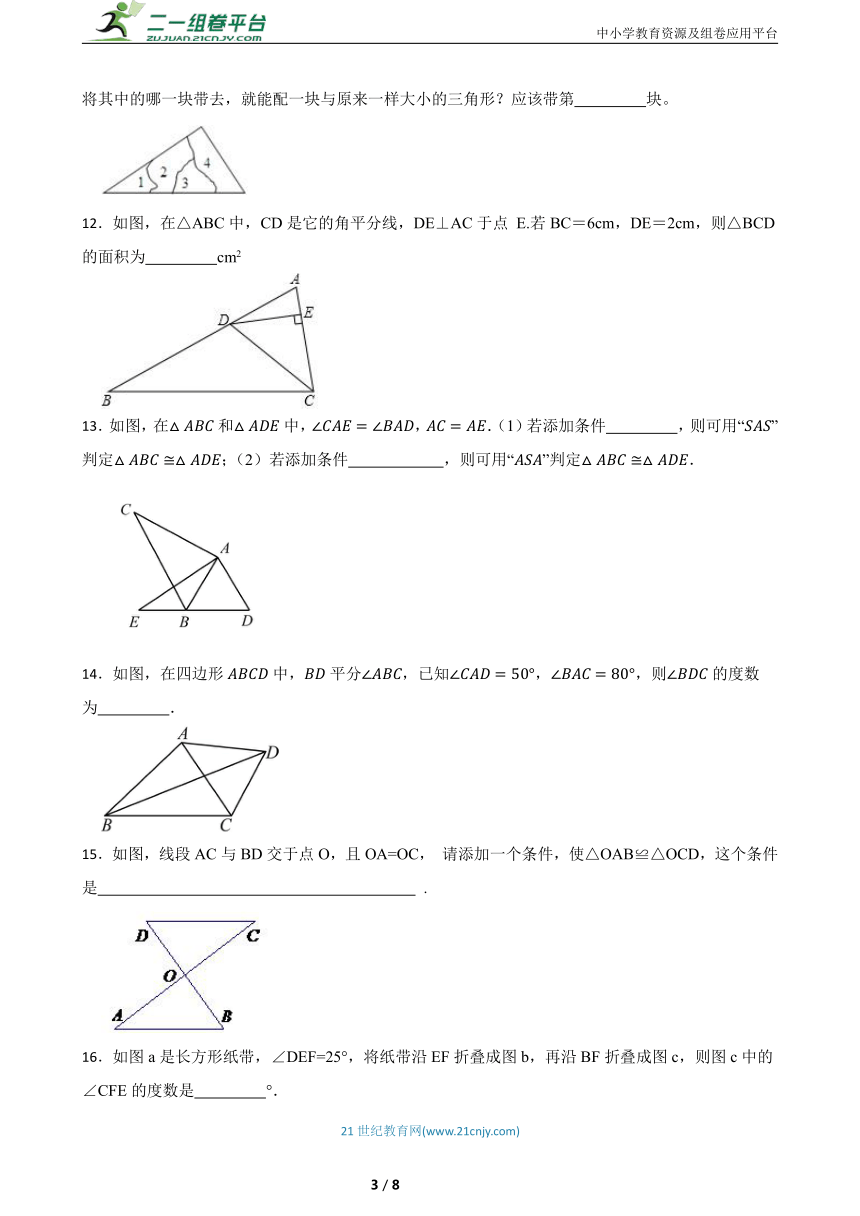
11.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形?应该带第 块。
12.如图,在△ABC中,CD是它的角平分线,DE⊥AC于点 E.若BC=6cm,DE=2cm,则△BCD的面积为 cm2
13.如图,在和中,,.(1)若添加条件 ,则可用“”判定;(2)若添加条件 ,则可用“”判定.
14.如图,在四边形中,平分,已知,,则的度数为 .
15.如图,线段AC与BD交于点O,且OA=OC, 请添加一个条件,使△OAB≌△OCD,这个条件是 .
16.如图a是长方形纸带,∠DEF=25°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是 °.
三、计算题
17.如图,直线,相交于点O,平分.
(1)若,求的度数;
(2)若,求的度数.
18.已知如图,,,,垂足分别为点,,;求证:.
19.综合与实践
问题情境
在数学活动课上,老师和同学们以“线段与角的共性”为主题开展数学活动.发现线段的中点的概念与角的平分线的概念类似,甚至它们在计算的方法上也有类似之处,它们之间的题目可以转换,解法可以互相借鉴.如图1,点是线段上的一点,是的中点,是的中点.
图1 图2 图3
(1)问题探究
①若,,求的长度;(写出计算过程)
②若,,则___________;(直接写出结果)
(2)继续探究
“创新”小组的同学类比想到:如图2,已知,在角的内部作射线,再分别作和的角平分线,.
③若,求的度数;(写出计算过程)
④若,则_____________;(直接写出结果)
(3)深入探究
“慎密”小组在“创新”小组的基础上提出:如图3,若,在角的外部作射线,再分别作和的角平分线,,若,则__________.(直接写出结果)
四、解答题
20.如图,点E、F分别在正方形ABCD的边DC、BC上,AG⊥EF,垂足为G,且AG=AB,则∠EAF为多少度.
21.已知:如图所示,B、C、E三点在同一条直线上,AC=CD,∠B=∠E=90°,AB=CE,AB=12,DE=5,求BE的长度.
22.如图,点、、、在一条直线上,,,求证:
(1)≌;
(2).
23.五边形ABCDE的对角线AC、AD分别平分和,若,试证明:.
答案解析部分
1.【答案】A
【知识点】三角形的外角性质;三角形全等的判定-SAS
2.【答案】A
【知识点】三角形全等及其性质
3.【答案】D
【知识点】平行线的判定;三角形全等的判定-SSS;尺规作图-作一个角等于已知角
4.【答案】A
【知识点】三角形全等及其性质
5.【答案】B
【知识点】平行线的性质;角平分线的性质
6.【答案】B
【知识点】三角形全等及其性质;三角形相关概念
7.【答案】B
【知识点】直角三角形全等的判定-HL;角平分线的性质
8.【答案】D
【知识点】角平分线的性质
9.【答案】D
【知识点】三角形全等的判定-ASA
10.【答案】C
【知识点】三角形全等及其性质;三角形全等的判定
11.【答案】4
【知识点】三角形全等的判定-ASA
12.【答案】6
【知识点】三角形的面积;角平分线的性质
13.【答案】;
【知识点】三角形全等的判定-SAS
14.【答案】
【知识点】三角形的外角性质;角平分线的性质;角平分线的判定
15.【答案】∠A=∠C,或∠B=∠D,或OD=OB或AB∥CD
【知识点】三角形全等的判定
16.【答案】105°
【知识点】三角形内角和定理;角平分线的性质;邻补角;内错角的概念
17.【答案】(1)
(2)
【知识点】角平分线的性质;对顶角及其性质;邻补角
18.【答案】证明:∵AE⊥BC,DF⊥BC,
∴∠AEB=∠CFD=90°,
∵CE=BF,EF=EF,
∴CF=BE,
在Rt△CDF和Rt△BAE中,
,
∴Rt△CDF≌Rt△BAE(HL),
∴∠A=∠D.
【知识点】直角三角形全等的判定-HL
19.【答案】(1)①3;②;(2)③40;④40;(3)
【知识点】角平分线的性质;线段的和、差、倍、分的简单计算
20.【答案】解:在Rt△ABF与Rt△AGF中,∵AB=AG,AF=AF,∠B=∠G=90°,∴△ABF≌△AGF(HL),∴∠BAF=∠GAF,同理易得:△AGE≌△ADE,有∠GAE=∠DAE;即∠EAF=∠EAG+∠FAG= ∠DAG+ ∠BAG= ∠DAB=45°,故∠EAF=45°
【知识点】全等三角形的判定与性质
21.【答案】解:在Rt△ABC和Rt△CDE中
AC=CD,AB=CE=12
∴△ABC≌△CDE
∴DE=BC=5
∴BE=CE+BC=12+5=17
【知识点】全等三角形的判定与性质
22.【答案】(1)证明:
,
,
,
在和中,,
所以≌;
(2)解:由可知≌,
所以,
所以.
【知识点】平行线的判定;三角形全等的判定-SSS
23.【答案】证明:在CD上取CF=BC,连接AF.
∵
∴
∵AC分别平分
∴
在与中,
∴
∴
同理可证:
∴,
∴ .
【知识点】三角形全等的判定-SAS
21世纪教育网(www.21cnjy.com)
2 / 9
【期末专项复习】人教版数学八年级上册“全等三角形”综合检测题
一、单选题
1.如图,BD=BC,BE=CA,∠DBE=∠C=62°,∠BDE=75°,则∠AFE的度数等于( )
A.148° B.140° C.135° D.128°
2.两个直角三角形中:①一锐角和斜边对应相等;②斜边一直角边对应相等;③有两条边相等;④两个锐角对应相等.其中能使这两个直角三角形全等的是( )
A.①② B.②③ C.①②③ D.①③④
3.如图,点C在的边上,尺规作图痕迹显示的是( )
A.作线段的垂直平分线 B.作的平分线
C.是等边三角形 D.作
4.已知图中的两个三角形全等,则等于( )
A. B. C. D.
5.如图,,,平分,则的大小为( )
A. B. C. D.
6.如图,在的长方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形.图中的为格点三角形,以点C为顶点的三角形最多能再画出( )个不同的格点三角形与全等.
A.8 B.9 C.10 D.11
7.如图,在中,,,平分,交于点,于点,且,则的周长为( )
A. B. C. D.不能确定
8.三条相互交叉的公路,现要建一个货物转运站,要求它到三条公路的距离相等,则可供选择的地址有( ).
A.1个 B.2个 C.3个 D.4个
9.一块三角形玻璃不小心打碎了,带上如图所示的玻璃碎片就能让玻璃店的师父重配一块与原来相同的三角形玻璃的依据是( )
A.SSS B.SAS C.AAS D.ASA
10.如图,AD是 的中线,E是AD上一点,连接BE并延长交AC于点F,若EF=AF,BE=7.5,CF=6,则EF=( ).
A.2.5 B.2 C.1.5 D.1
二、填空题
11.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形?应该带第 块。
12.如图,在△ABC中,CD是它的角平分线,DE⊥AC于点 E.若BC=6cm,DE=2cm,则△BCD的面积为 cm2
13.如图,在和中,,.(1)若添加条件 ,则可用“”判定;(2)若添加条件 ,则可用“”判定.
14.如图,在四边形中,平分,已知,,则的度数为 .
15.如图,线段AC与BD交于点O,且OA=OC, 请添加一个条件,使△OAB≌△OCD,这个条件是 .
16.如图a是长方形纸带,∠DEF=25°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是 °.
三、计算题
17.如图,直线,相交于点O,平分.
(1)若,求的度数;
(2)若,求的度数.
18.已知如图,,,,垂足分别为点,,;求证:.
19.综合与实践
问题情境
在数学活动课上,老师和同学们以“线段与角的共性”为主题开展数学活动.发现线段的中点的概念与角的平分线的概念类似,甚至它们在计算的方法上也有类似之处,它们之间的题目可以转换,解法可以互相借鉴.如图1,点是线段上的一点,是的中点,是的中点.
图1 图2 图3
(1)问题探究
①若,,求的长度;(写出计算过程)
②若,,则___________;(直接写出结果)
(2)继续探究
“创新”小组的同学类比想到:如图2,已知,在角的内部作射线,再分别作和的角平分线,.
③若,求的度数;(写出计算过程)
④若,则_____________;(直接写出结果)
(3)深入探究
“慎密”小组在“创新”小组的基础上提出:如图3,若,在角的外部作射线,再分别作和的角平分线,,若,则__________.(直接写出结果)
四、解答题
20.如图,点E、F分别在正方形ABCD的边DC、BC上,AG⊥EF,垂足为G,且AG=AB,则∠EAF为多少度.
21.已知:如图所示,B、C、E三点在同一条直线上,AC=CD,∠B=∠E=90°,AB=CE,AB=12,DE=5,求BE的长度.
22.如图,点、、、在一条直线上,,,求证:
(1)≌;
(2).
23.五边形ABCDE的对角线AC、AD分别平分和,若,试证明:.
答案解析部分
1.【答案】A
【知识点】三角形的外角性质;三角形全等的判定-SAS
2.【答案】A
【知识点】三角形全等及其性质
3.【答案】D
【知识点】平行线的判定;三角形全等的判定-SSS;尺规作图-作一个角等于已知角
4.【答案】A
【知识点】三角形全等及其性质
5.【答案】B
【知识点】平行线的性质;角平分线的性质
6.【答案】B
【知识点】三角形全等及其性质;三角形相关概念
7.【答案】B
【知识点】直角三角形全等的判定-HL;角平分线的性质
8.【答案】D
【知识点】角平分线的性质
9.【答案】D
【知识点】三角形全等的判定-ASA
10.【答案】C
【知识点】三角形全等及其性质;三角形全等的判定
11.【答案】4
【知识点】三角形全等的判定-ASA
12.【答案】6
【知识点】三角形的面积;角平分线的性质
13.【答案】;
【知识点】三角形全等的判定-SAS
14.【答案】
【知识点】三角形的外角性质;角平分线的性质;角平分线的判定
15.【答案】∠A=∠C,或∠B=∠D,或OD=OB或AB∥CD
【知识点】三角形全等的判定
16.【答案】105°
【知识点】三角形内角和定理;角平分线的性质;邻补角;内错角的概念
17.【答案】(1)
(2)
【知识点】角平分线的性质;对顶角及其性质;邻补角
18.【答案】证明:∵AE⊥BC,DF⊥BC,
∴∠AEB=∠CFD=90°,
∵CE=BF,EF=EF,
∴CF=BE,
在Rt△CDF和Rt△BAE中,
,
∴Rt△CDF≌Rt△BAE(HL),
∴∠A=∠D.
【知识点】直角三角形全等的判定-HL
19.【答案】(1)①3;②;(2)③40;④40;(3)
【知识点】角平分线的性质;线段的和、差、倍、分的简单计算
20.【答案】解:在Rt△ABF与Rt△AGF中,∵AB=AG,AF=AF,∠B=∠G=90°,∴△ABF≌△AGF(HL),∴∠BAF=∠GAF,同理易得:△AGE≌△ADE,有∠GAE=∠DAE;即∠EAF=∠EAG+∠FAG= ∠DAG+ ∠BAG= ∠DAB=45°,故∠EAF=45°
【知识点】全等三角形的判定与性质
21.【答案】解:在Rt△ABC和Rt△CDE中
AC=CD,AB=CE=12
∴△ABC≌△CDE
∴DE=BC=5
∴BE=CE+BC=12+5=17
【知识点】全等三角形的判定与性质
22.【答案】(1)证明:
,
,
,
在和中,,
所以≌;
(2)解:由可知≌,
所以,
所以.
【知识点】平行线的判定;三角形全等的判定-SSS
23.【答案】证明:在CD上取CF=BC,连接AF.
∵
∴
∵AC分别平分
∴
在与中,
∴
∴
同理可证:
∴,
∴ .
【知识点】三角形全等的判定-SAS
21世纪教育网(www.21cnjy.com)
2 / 9
