15.1.1从分数到分式 教学设计 人教版数学八年级上册
文档属性
| 名称 | 15.1.1从分数到分式 教学设计 人教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 176.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-15 09:20:52 | ||
图片预览

文档简介
教学设计
课题 《从分数到分式》
课型 新授课 复习课□ 试卷讲评课□ 其它课□
教学内容分析 本节课是人教版八年级下册第十六章第一节《分式》的第一小节《从分数到分式》,属于数与代数领域的教学内容,是初中数学中继整式之后学习的又一代数的基础知识,又是对小学所学知识的延伸和拓展。本节分式的学习是本章继续学习分式的性质、运算以及解分式方程的基础和前提,它是以分数知识为基础,类比引出分式的概念,把学生对“式”的认识由整式扩充到有理式。
学情分析 学生已经学习过分数及其运算,这为分式的学习奠定了知识基础,提供了学习经验,并且学生初步具备了“观察、分析、归纳”的基本能力。但是学生对于为什么要学习分式,为什么可以将分式与分数类比,怎样进行类比等一系列问题很少考虑,但这些问题又非常关键。因而达成教学目标,学生还需要明白在根据情境提出问题、解决问题的过程中,利用类比的思想研究问题,从而有效地突破重点和难点,获得研究一类问题的方法。 因此,本节课的难点是:明白为何可以类比分数、怎样类比分数研究分式的内容。
学习目标 (1)了解分式的概念,明确分式和整式的区别; (2)体会分式的意义,进一步发展符号感,掌握分式的符号法则; (3)经历分式探索,体会并掌握有效的数学转化思想; (4)能解决一些简单的实际问题,进一步体会分式的模型思想。
重难点 (1)了解分式的概念,明确分式和整式的区别; (2)体会分式的意义,进一步发展符号感,掌握分式的符号法则;
评价任务 在学生已有数学经验的基础上,探求新知,从而获得成功的快乐,提高学生“用数学”意识; 在活动中培养学生乐于探究合作学习的习惯,培养学生努力寻找解决问题的进取心,体会数学的应用价值; 经历建立分式方程模型解决实际问题的过程,体会数学模型的应用价值,从而提高学习数学的兴趣。
教学评活动过程 教师活动学生活动环节一:(创设情境,导入新知)教师活动 1、回顾单项式、多项式以及整式的概念。 2、在古诗词中,有很多作品都蕴含着有趣的数学问题.唐朝诗人李白《早发白帝城》:“朝辞白帝彩云间,千里江陵一日还.” 思考:若李白在现代,“千里江陵”能否“一日还” 列式表示下列各量,其中 (1)~(2) 不考虑江水流速: (1) 如果行船速度为 v 千米/时,那么半日( 12 小时)行船距离是______千米; (2) 如果行船距离为 s 千米,船速为 v 千米/时,那么用时________小时; (3) 如果距离为 180 千米,船在静水中的航速为 ( > 8) 千米/时,江水流速为 8 千米/时,那么由白帝城顺流而下到江陵的速度为______千米/时,需_______小时. 学生活动 首先,带着学生复习七年级学过的单项式,多项式和整式;然后,由学生熟悉的唐诗《早发白帝城》导入,以这首诗为背景提出问题,通过跨学科联动,充分调动学生学习的兴趣.古诗的导入,使得学生对知识点的记忆更加深刻. 引导学生用列式表示下列各量,表示判断若是现代李白“千里江陵”能否“一日还”,需要了解哪些实际数据,然后可以课后查找实际数据来判断这个. (学生积极踊跃发言,问答提出的问题.)
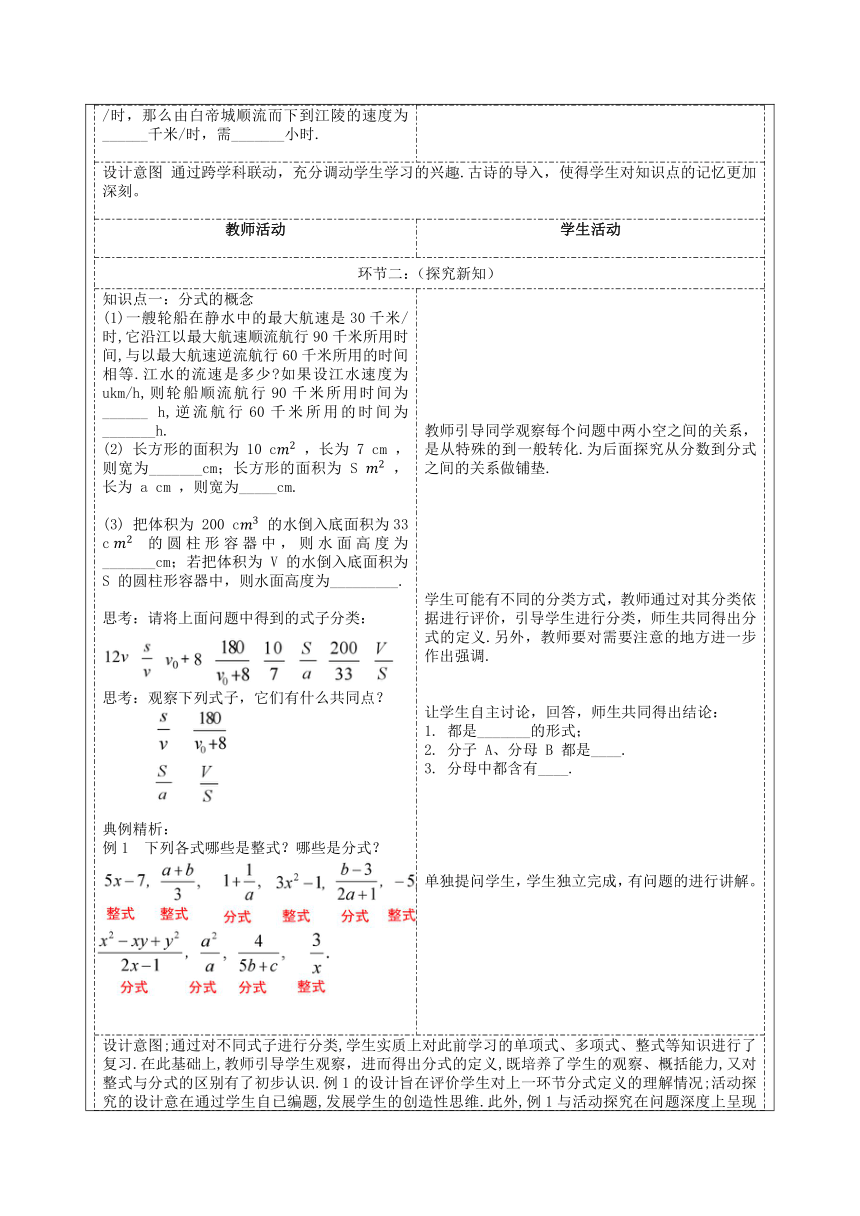
设计意图 通过跨学科联动,充分调动学生学习的兴趣.古诗的导入,使得学生对知识点的记忆更加深刻。 教师活动 学生活动 环节二:(探究新知)知识点一:分式的概念 (1)一艘轮船在静水中的最大航速是30千米/时,它沿江以最大航速顺流航行90千米所用时间,与以最大航速逆流航行60千米所用的时间相等.江水的流速是多少 如果设江水速度为ukm/h,则轮船顺流航行90千米所用时间为______ h,逆流航行60千米所用的时间为_______h. (2) 长方形的面积为 10 c ,长为 7 cm ,则宽为_______cm;长方形的面积为 S ,长为 a cm ,则宽为_____cm. (3) 把体积为 200 c 的水倒入底面积为33 c 的圆柱形容器中,则水面高度为_______cm;若把体积为 V 的水倒入底面积为 S 的圆柱形容器中,则水面高度为_________. 思考:请将上面问题中得到的式子分类: 思考:观察下列式子,它们有什么共同点? 典例精析: 例1 下列各式哪些是整式?哪些是分式? 教师引导同学观察每个问题中两小空之间的关系,是从特殊的到一般转化.为后面探究从分数到分式之间的关系做铺垫. 学生可能有不同的分类方式,教师通过对其分类依据进行评价,引导学生进行分类,师生共同得出分式的定义.另外,教师要对需要注意的地方进一步作出强调. 让学生自主讨论,回答,师生共同得出结论: 1. 都是_______的形式; 2. 分子 A、分母 B 都是____. 3. 分母中都含有____. 单独提问学生,学生独立完成,有问题的进行讲解。设计意图;通过对不同式子进行分类,学生实质上对此前学习的单项式、多项式、整式等知识进行了复习.在此基础上,教师引导学生观察,进而得出分式的定义,既培养了学生的观察、概括能力,又对整式与分式的区别有了初步认识.例1的设计旨在评价学生对上一环节分式定义的理解情况;活动探究的设计意在通过学生自已编题,发展学生的创造性思维.此外,例1与活动探究在问题深度上呈现递进性,例1中的式子可以视为活动探究中学生“创造”的资源,这符合循序渐进的理念.知识点二:分式有意义的条件 想一想:分数在什么条件下有意义? 类比分数,分式在什么条件下有意义呢? 对于分式 : 当_B ≠ 0__时,分式有意义; 当 B = 0 时,分式无意义. 例2 下列分式中的字母满足什么条件时分式有意义? ;(6);(7) 让学生独立思考,再共同归纳总结: 教师给出例题后,让学生独立作业,同时分别选派四名同学上黑板演算前四道题. 教师巡视,对学生演算过程中的失误及时予以指正,接着,让学生先自己思考后三道题,对于难点进行点拨,最后师生共同评析。设计意图:从分数有意义的条件出发,类比分数有意义的条件,得出分式有意义,分式无意义的条件,让学生体会类比思想,凸显了数学学科重视思维培养的特点。知识点三:分式值为零的条件 例3:已知分式 (1)当x为何值时,分式无意义 (2) 当x为何值时,分式有意义 (3) 当x为何值时,分式的值为零? (4) 当x= - 3时,分式的值是多少 学生总结,老师补充,得出分式值为零的条件,分子等于零,分母不等于零。 在前面的基础下,前两道题学生很容易做出来,最重要的是探讨分式值为零需要满足的条件,让学生类比分数,通过小组讨论,得出答案。教师活动 学生活动环节三:(小结)教师提问学生,让学生谈收获学生自己总结知识点,谈收获设计意图:通过学生自己总结,学生的印象会更加深刻,知识点掌握的更加牢固。环节四:(当堂检测,巩固所学)限时完成课本上对应的试题,以及课时练上对应的例1、例2学生独立完成,挑选学生代表讲解易错题设计意图:巩固本节课学习的内容,当堂检测,看学生完成掌握的情况。
板书设计
作业与拓展学习设计 分层设计作业。每课时均设计“基础性作业”《面向全体,体现课标,题量3-4大题,要求学生必做》和“发展性作业”《体现个性化,探究性、实践性,题量2-4大题,要求学生有选择的完成)。
教学反思与改进 本节课从实际问题出发,类比分数得到分式的定义,分数的分子分母都是些具体的整数,分式的分子分母由这些整数推广到一般的整式,并且分母中一定含有字母,分式比分数更具有一般性。由分数到分式是由特殊到一般,由具体到抽象。分数不是分式,它是整式,整式和分式都是代数式。分式是反映实际问题中数量关系的一个重要的式子,它在解决实际问题中有着广泛的应用。 本节课是《分式》的第一节《从分数到分式》,是课时教学课型,是全章内容教学的基础,重在引导学生懂得为什么要学,将要学什么,如何学,自学、议论、引导的教学方法和手段贯穿整个课堂,类比、转化的数学思想方法研究问题. 通过本节课的学习,让学生对本章内容有个初步了解,对今后的学习有着重要的指导意义.
课题 《从分数到分式》
课型 新授课 复习课□ 试卷讲评课□ 其它课□
教学内容分析 本节课是人教版八年级下册第十六章第一节《分式》的第一小节《从分数到分式》,属于数与代数领域的教学内容,是初中数学中继整式之后学习的又一代数的基础知识,又是对小学所学知识的延伸和拓展。本节分式的学习是本章继续学习分式的性质、运算以及解分式方程的基础和前提,它是以分数知识为基础,类比引出分式的概念,把学生对“式”的认识由整式扩充到有理式。
学情分析 学生已经学习过分数及其运算,这为分式的学习奠定了知识基础,提供了学习经验,并且学生初步具备了“观察、分析、归纳”的基本能力。但是学生对于为什么要学习分式,为什么可以将分式与分数类比,怎样进行类比等一系列问题很少考虑,但这些问题又非常关键。因而达成教学目标,学生还需要明白在根据情境提出问题、解决问题的过程中,利用类比的思想研究问题,从而有效地突破重点和难点,获得研究一类问题的方法。 因此,本节课的难点是:明白为何可以类比分数、怎样类比分数研究分式的内容。
学习目标 (1)了解分式的概念,明确分式和整式的区别; (2)体会分式的意义,进一步发展符号感,掌握分式的符号法则; (3)经历分式探索,体会并掌握有效的数学转化思想; (4)能解决一些简单的实际问题,进一步体会分式的模型思想。
重难点 (1)了解分式的概念,明确分式和整式的区别; (2)体会分式的意义,进一步发展符号感,掌握分式的符号法则;
评价任务 在学生已有数学经验的基础上,探求新知,从而获得成功的快乐,提高学生“用数学”意识; 在活动中培养学生乐于探究合作学习的习惯,培养学生努力寻找解决问题的进取心,体会数学的应用价值; 经历建立分式方程模型解决实际问题的过程,体会数学模型的应用价值,从而提高学习数学的兴趣。
教学评活动过程 教师活动学生活动环节一:(创设情境,导入新知)教师活动 1、回顾单项式、多项式以及整式的概念。 2、在古诗词中,有很多作品都蕴含着有趣的数学问题.唐朝诗人李白《早发白帝城》:“朝辞白帝彩云间,千里江陵一日还.” 思考:若李白在现代,“千里江陵”能否“一日还” 列式表示下列各量,其中 (1)~(2) 不考虑江水流速: (1) 如果行船速度为 v 千米/时,那么半日( 12 小时)行船距离是______千米; (2) 如果行船距离为 s 千米,船速为 v 千米/时,那么用时________小时; (3) 如果距离为 180 千米,船在静水中的航速为 ( > 8) 千米/时,江水流速为 8 千米/时,那么由白帝城顺流而下到江陵的速度为______千米/时,需_______小时. 学生活动 首先,带着学生复习七年级学过的单项式,多项式和整式;然后,由学生熟悉的唐诗《早发白帝城》导入,以这首诗为背景提出问题,通过跨学科联动,充分调动学生学习的兴趣.古诗的导入,使得学生对知识点的记忆更加深刻. 引导学生用列式表示下列各量,表示判断若是现代李白“千里江陵”能否“一日还”,需要了解哪些实际数据,然后可以课后查找实际数据来判断这个. (学生积极踊跃发言,问答提出的问题.)
设计意图 通过跨学科联动,充分调动学生学习的兴趣.古诗的导入,使得学生对知识点的记忆更加深刻。 教师活动 学生活动 环节二:(探究新知)知识点一:分式的概念 (1)一艘轮船在静水中的最大航速是30千米/时,它沿江以最大航速顺流航行90千米所用时间,与以最大航速逆流航行60千米所用的时间相等.江水的流速是多少 如果设江水速度为ukm/h,则轮船顺流航行90千米所用时间为______ h,逆流航行60千米所用的时间为_______h. (2) 长方形的面积为 10 c ,长为 7 cm ,则宽为_______cm;长方形的面积为 S ,长为 a cm ,则宽为_____cm. (3) 把体积为 200 c 的水倒入底面积为33 c 的圆柱形容器中,则水面高度为_______cm;若把体积为 V 的水倒入底面积为 S 的圆柱形容器中,则水面高度为_________. 思考:请将上面问题中得到的式子分类: 思考:观察下列式子,它们有什么共同点? 典例精析: 例1 下列各式哪些是整式?哪些是分式? 教师引导同学观察每个问题中两小空之间的关系,是从特殊的到一般转化.为后面探究从分数到分式之间的关系做铺垫. 学生可能有不同的分类方式,教师通过对其分类依据进行评价,引导学生进行分类,师生共同得出分式的定义.另外,教师要对需要注意的地方进一步作出强调. 让学生自主讨论,回答,师生共同得出结论: 1. 都是_______的形式; 2. 分子 A、分母 B 都是____. 3. 分母中都含有____. 单独提问学生,学生独立完成,有问题的进行讲解。设计意图;通过对不同式子进行分类,学生实质上对此前学习的单项式、多项式、整式等知识进行了复习.在此基础上,教师引导学生观察,进而得出分式的定义,既培养了学生的观察、概括能力,又对整式与分式的区别有了初步认识.例1的设计旨在评价学生对上一环节分式定义的理解情况;活动探究的设计意在通过学生自已编题,发展学生的创造性思维.此外,例1与活动探究在问题深度上呈现递进性,例1中的式子可以视为活动探究中学生“创造”的资源,这符合循序渐进的理念.知识点二:分式有意义的条件 想一想:分数在什么条件下有意义? 类比分数,分式在什么条件下有意义呢? 对于分式 : 当_B ≠ 0__时,分式有意义; 当 B = 0 时,分式无意义. 例2 下列分式中的字母满足什么条件时分式有意义? ;(6);(7) 让学生独立思考,再共同归纳总结: 教师给出例题后,让学生独立作业,同时分别选派四名同学上黑板演算前四道题. 教师巡视,对学生演算过程中的失误及时予以指正,接着,让学生先自己思考后三道题,对于难点进行点拨,最后师生共同评析。设计意图:从分数有意义的条件出发,类比分数有意义的条件,得出分式有意义,分式无意义的条件,让学生体会类比思想,凸显了数学学科重视思维培养的特点。知识点三:分式值为零的条件 例3:已知分式 (1)当x为何值时,分式无意义 (2) 当x为何值时,分式有意义 (3) 当x为何值时,分式的值为零? (4) 当x= - 3时,分式的值是多少 学生总结,老师补充,得出分式值为零的条件,分子等于零,分母不等于零。 在前面的基础下,前两道题学生很容易做出来,最重要的是探讨分式值为零需要满足的条件,让学生类比分数,通过小组讨论,得出答案。教师活动 学生活动环节三:(小结)教师提问学生,让学生谈收获学生自己总结知识点,谈收获设计意图:通过学生自己总结,学生的印象会更加深刻,知识点掌握的更加牢固。环节四:(当堂检测,巩固所学)限时完成课本上对应的试题,以及课时练上对应的例1、例2学生独立完成,挑选学生代表讲解易错题设计意图:巩固本节课学习的内容,当堂检测,看学生完成掌握的情况。
板书设计
作业与拓展学习设计 分层设计作业。每课时均设计“基础性作业”《面向全体,体现课标,题量3-4大题,要求学生必做》和“发展性作业”《体现个性化,探究性、实践性,题量2-4大题,要求学生有选择的完成)。
教学反思与改进 本节课从实际问题出发,类比分数得到分式的定义,分数的分子分母都是些具体的整数,分式的分子分母由这些整数推广到一般的整式,并且分母中一定含有字母,分式比分数更具有一般性。由分数到分式是由特殊到一般,由具体到抽象。分数不是分式,它是整式,整式和分式都是代数式。分式是反映实际问题中数量关系的一个重要的式子,它在解决实际问题中有着广泛的应用。 本节课是《分式》的第一节《从分数到分式》,是课时教学课型,是全章内容教学的基础,重在引导学生懂得为什么要学,将要学什么,如何学,自学、议论、引导的教学方法和手段贯穿整个课堂,类比、转化的数学思想方法研究问题. 通过本节课的学习,让学生对本章内容有个初步了解,对今后的学习有着重要的指导意义.
