第十七章 勾股定理 学情评估卷(含答案) 人教版数学八年级下册
文档属性
| 名称 | 第十七章 勾股定理 学情评估卷(含答案) 人教版数学八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 252.0KB | ||
| 资源类型 | 教案 | ||
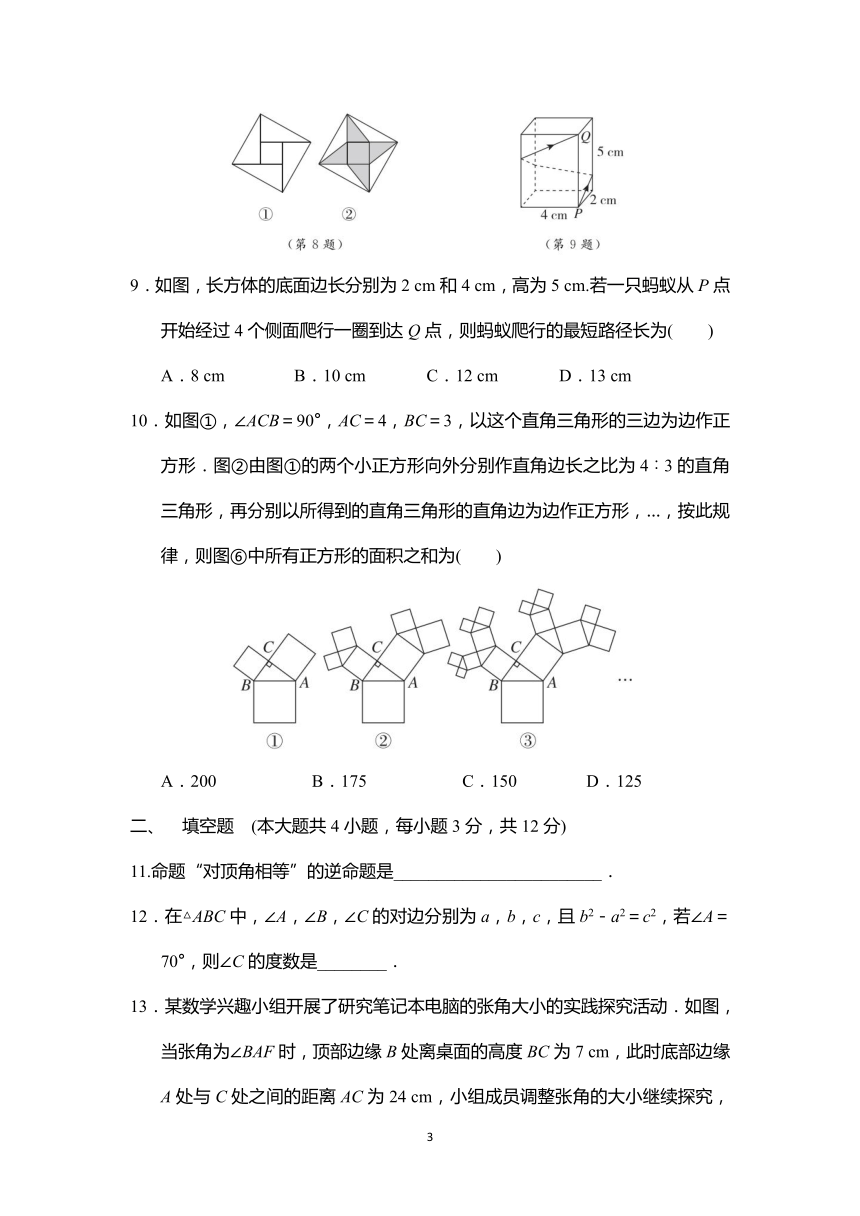
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-15 00:00:00 | ||
图片预览




文档简介
第十七章 学情评估卷
一、 选择题 (本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的)
1.直角三角形的两条直角边的长分别为1,,则其斜边的长为( )
A.3 B.2 C.4 D.2
2.下列各组数中,是勾股数的是( )
A.9,16,25 B.,,2
C.1.5,2,2.5 D.5,12,13
3.如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,则正方形ABDE的面积为( )
A.81 B.144 C.225 D.169
4.在平面直角坐标系中,有四个点P,Q(-,),M(-2,),N(,2),则这四个点中到原点距离最远的是( )
A.P B.Q C.M D.N
5.如图,长方形ABCD的边AD在数轴上,点A表示数-1,点D表示数-4,AB=1,以点A为圆心,AC的长为半径作弧,与数轴负半轴交于点E,则点E表示的数为( )
A.- B.-1- C.- D.-1-
6.由下列条件不能判定△ABC为直角三角形的是( )
A.∠A+∠B=∠C
B.∠A∶∠B∶∠C=1∶2∶3
C.AB=3k,BC=4k,AC=5k(k为正整数)
D.AC=3+k,AB=4+k,BC=5+k(k>0)
7.如图,在△ABC中,分别以点A,B为圆心,以大于AB的长为半径作弧,两弧相交于F,G两点,作直线FG分别交AB,BC于点M,D;再分别以点A,C为圆心,以大于AC的长为半径作弧,两弧相交于H,I两点,作直线HI分别交AC,BC于点N,E.若BD=,DE=2,EC=,则AC的长为( )
A. B. C. D.
8.如图,四个全等的直角三角形围成一个大正方形,中间是个小正方形.这个图形是我国古代数学家赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.现分别连接大、小正方形的四组顶点得到图②的“风车”图案(阴影部分).若图①中的四个直角三角形的较长直角边长为9,较短直角边长为5,则图②中的“风车”图案的周长为( )
A.16+4 B.16+4 C.20+4 D.20+4
9.如图,长方体的底面边长分别为2 cm和4 cm,高为5 cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为( )
A.8 cm B.10 cm C.12 cm D.13 cm
10.如图①,∠ACB=90°,AC=4,BC=3,以这个直角三角形的三边为边作正方形.图②由图①的两个小正方形向外分别作直角边长之比为4∶3的直角三角形,再分别以所得到的直角三角形的直角边为边作正方形,…,按此规律,则图⑥中所有正方形的面积之和为( )
A.200 B.175 C.150 D.125
二、 填空题 (本大题共4小题,每小题3分,共12分)
11.命题“对顶角相等”的逆命题是________________________.
12.在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,且b2-a2=c2,若∠A=70°,则∠C的度数是________.
13.某数学兴趣小组开展了研究笔记本电脑的张角大小的实践探究活动.如图,当张角为∠BAF时,顶部边缘B处离桌面的高度BC为7 cm,此时底部边缘A处与C处之间的距离AC为24 cm,小组成员调整张角的大小继续探究,最后发现当张角为∠DAF时(D是B的对应点),顶部边缘D处到桌面的距离DE为20 cm,则底部边缘A处与E处之间的距离AE为________.
14.如图,在Rt△ABC中,∠ACB=90°,点P为BC上一个动点,连接AP,将△ACP沿AP折叠得到△ADP,点C的对应点为点D,连接BD,若AC=5,BC=12,当△PBD为直角三角形时,线段CP的长为__________.
三、 解答题 (本大题共4小题,共58分.解答时应写出文字说明、证明过程或演算步骤)
15.(12分)如图,在四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°,求证:∠A+∠C=180°.
16.(12分)将边长分别为a和2b(a>b)的长方形分割成四个全等的直角三角形,如图①,再用这四个三角形拼成如图②所示的大正方形,中间形成一个小正方形的空洞.经测量得长方形的面积为24,大正方形的边长为5.试通过你获取的信息,求a2+b2和a2-b2的值.
17.(16分)钓鱼岛及其附属岛屿是中国的固有领土,我国对钓鱼岛的巡航已经常态化.如图,甲、乙两艘海警船同时从位于南北方向的海岸线AB上的某港口P出发,各自沿一固定方向对钓鱼岛巡航,已知甲船每小时航行12海里,乙船每小时航行16海里.
(1)若甲、乙两船离开港口一个半小时后分别位于Q,R处(图①),且相距30海里,如果知道甲船沿北偏东70°方向航行,那么你知道乙船沿哪个方向航行吗?请说明理由;
(2)若甲船沿北偏东60°方向航行(图②),从港口P离开经过两个小时后位于点C处,此时船上有名海警需要以最快的速度回到PA海岸线上,若他从C处出发,乘坐的快艇的速度是每小时90海里,他能在14分钟内回到海岸线吗?请说明理由.(提示:≈1.7)
18.(18分)【问题提出】
(1)如图①,△ABC和△DCE都是等边三角形,点D在△ABC内部,连接AD,AE,BD.
①求证:BD=AE;
②若∠ADC=150°,求证:BD2=AD2+CD2;
【问题探究】
(2)如图②,△ABC和△DCE都是等边三角形,点D在△ABC外部,若BD2=AD2+CD2仍然成立,求∠ADC的度数;
【问题拓展】
(3)如图③,在△ABC中,AB=AC,∠BAC=90°,点D为△ABC外一点.若∠ADC=45°,BD=,CD=,请直接写出AD的长.
答案
答案速查 1 2 3 4 5 6 7 8 9 10
D D C B D D A C D B
11.相等的两个角为对顶角 12.20° 13.15 cm 14.或5
15.证明:连接AC.∵AB=20,BC=15,∠B=90°,
∴由勾股定理,得AC2=202+152=625.
∵CD=7,AD=24,∴CD2+AD2=625,
∴AC2=CD2+AD2,∴∠D=90°,
∴∠A+∠C=360°-180°=180°.
16.解:根据题意得a2+b2=52=25,a·2b=24,
∴a2+b2+2ab=49,∴a+b=7,
由题图②得(a-b)2=25-24=1,
∵a>b,∴a-b=1,
∴a2-b2=(a+b)(a-b)=7×1=7.
17.解:(1)乙船沿南偏东20° 方向航行.
理由如下:由题意得∠APQ=70°,PQ=12×1.5=18(海里),
PR=16×1.5=24(海里),
在△PQR中,∵PQ2+PR2=182+242=900,QR2=302=900,
∴PQ2+PR2=QR2,
∴△PQR是直角三角形,∠QPR=90°,
∴∠BPR=180°-∠APQ-∠QPR=180°-70°-90°=20°,
∴乙船沿南偏东20°方向航行.
(2)能,理由如下:如图,过点C作CD⊥AB于点D,
由题意知∠CPD=60°,PC=2×12=24(海里),
∴∠C=30°,∴PD=PC=12海里,
∴CD==12 ≈20.4(海里).
∵90×=21(海里),21>20.4,
∴他能在14分钟内回到海岸线.
18.(1)证明:①∵△ABC和△DCE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠BCD=∠ACE,∴△CBD≌△CAE,∴BD=AE.
②∵△DCE为等边三角形,∴∠EDC=60°,DE=CD.
∵∠ADC=150°,∴∠ADE=150°-60°=90°,
∴AD2+DE2=AE2.
由①知BD=AE,∴BD2=AD2+CD2.
(2)解:∵△ABC和△DCE都是等边三角形,
∴AC=BC,CD=CE=DE,∠ACB=∠DCE=∠CDE=60°,∴∠BCD=∠ACE,
∴△CBD≌△CAE,∴BD=AE,
∵BD2=AD2+CD2,
∴AE2=AD2+DE2,∴∠ADE=90°,
∴∠ADC=∠ADE-∠CDE=90°-60°=30°.
(3)解:AD的长为3.
点拨:如图,过点A作AE⊥AD,使AE=AD,连接DE,CE,则∠ADE=45°.
∵∠EAD=∠BAC=90°,
∴∠BAD=∠CAE.
又∵AB=AC,AD=AE,
∴△ABD≌△ACE,
∴BD=CE.
∵BD=,
∴CE=.
∵∠ADC=45°,∠ADE=45°,
∴∠CDE=90°,
∵CD=,
∴DE2=CE2-CD2=2-2=18,
在Rt△ADE中,∵∠EAD=90°,∴AE2+AD2=DE2,∴2AD2=18,∴AD=3.
一、 选择题 (本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的)
1.直角三角形的两条直角边的长分别为1,,则其斜边的长为( )
A.3 B.2 C.4 D.2
2.下列各组数中,是勾股数的是( )
A.9,16,25 B.,,2
C.1.5,2,2.5 D.5,12,13
3.如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,则正方形ABDE的面积为( )
A.81 B.144 C.225 D.169
4.在平面直角坐标系中,有四个点P,Q(-,),M(-2,),N(,2),则这四个点中到原点距离最远的是( )
A.P B.Q C.M D.N
5.如图,长方形ABCD的边AD在数轴上,点A表示数-1,点D表示数-4,AB=1,以点A为圆心,AC的长为半径作弧,与数轴负半轴交于点E,则点E表示的数为( )
A.- B.-1- C.- D.-1-
6.由下列条件不能判定△ABC为直角三角形的是( )
A.∠A+∠B=∠C
B.∠A∶∠B∶∠C=1∶2∶3
C.AB=3k,BC=4k,AC=5k(k为正整数)
D.AC=3+k,AB=4+k,BC=5+k(k>0)
7.如图,在△ABC中,分别以点A,B为圆心,以大于AB的长为半径作弧,两弧相交于F,G两点,作直线FG分别交AB,BC于点M,D;再分别以点A,C为圆心,以大于AC的长为半径作弧,两弧相交于H,I两点,作直线HI分别交AC,BC于点N,E.若BD=,DE=2,EC=,则AC的长为( )
A. B. C. D.
8.如图,四个全等的直角三角形围成一个大正方形,中间是个小正方形.这个图形是我国古代数学家赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.现分别连接大、小正方形的四组顶点得到图②的“风车”图案(阴影部分).若图①中的四个直角三角形的较长直角边长为9,较短直角边长为5,则图②中的“风车”图案的周长为( )
A.16+4 B.16+4 C.20+4 D.20+4
9.如图,长方体的底面边长分别为2 cm和4 cm,高为5 cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为( )
A.8 cm B.10 cm C.12 cm D.13 cm
10.如图①,∠ACB=90°,AC=4,BC=3,以这个直角三角形的三边为边作正方形.图②由图①的两个小正方形向外分别作直角边长之比为4∶3的直角三角形,再分别以所得到的直角三角形的直角边为边作正方形,…,按此规律,则图⑥中所有正方形的面积之和为( )
A.200 B.175 C.150 D.125
二、 填空题 (本大题共4小题,每小题3分,共12分)
11.命题“对顶角相等”的逆命题是________________________.
12.在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,且b2-a2=c2,若∠A=70°,则∠C的度数是________.
13.某数学兴趣小组开展了研究笔记本电脑的张角大小的实践探究活动.如图,当张角为∠BAF时,顶部边缘B处离桌面的高度BC为7 cm,此时底部边缘A处与C处之间的距离AC为24 cm,小组成员调整张角的大小继续探究,最后发现当张角为∠DAF时(D是B的对应点),顶部边缘D处到桌面的距离DE为20 cm,则底部边缘A处与E处之间的距离AE为________.
14.如图,在Rt△ABC中,∠ACB=90°,点P为BC上一个动点,连接AP,将△ACP沿AP折叠得到△ADP,点C的对应点为点D,连接BD,若AC=5,BC=12,当△PBD为直角三角形时,线段CP的长为__________.
三、 解答题 (本大题共4小题,共58分.解答时应写出文字说明、证明过程或演算步骤)
15.(12分)如图,在四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°,求证:∠A+∠C=180°.
16.(12分)将边长分别为a和2b(a>b)的长方形分割成四个全等的直角三角形,如图①,再用这四个三角形拼成如图②所示的大正方形,中间形成一个小正方形的空洞.经测量得长方形的面积为24,大正方形的边长为5.试通过你获取的信息,求a2+b2和a2-b2的值.
17.(16分)钓鱼岛及其附属岛屿是中国的固有领土,我国对钓鱼岛的巡航已经常态化.如图,甲、乙两艘海警船同时从位于南北方向的海岸线AB上的某港口P出发,各自沿一固定方向对钓鱼岛巡航,已知甲船每小时航行12海里,乙船每小时航行16海里.
(1)若甲、乙两船离开港口一个半小时后分别位于Q,R处(图①),且相距30海里,如果知道甲船沿北偏东70°方向航行,那么你知道乙船沿哪个方向航行吗?请说明理由;
(2)若甲船沿北偏东60°方向航行(图②),从港口P离开经过两个小时后位于点C处,此时船上有名海警需要以最快的速度回到PA海岸线上,若他从C处出发,乘坐的快艇的速度是每小时90海里,他能在14分钟内回到海岸线吗?请说明理由.(提示:≈1.7)
18.(18分)【问题提出】
(1)如图①,△ABC和△DCE都是等边三角形,点D在△ABC内部,连接AD,AE,BD.
①求证:BD=AE;
②若∠ADC=150°,求证:BD2=AD2+CD2;
【问题探究】
(2)如图②,△ABC和△DCE都是等边三角形,点D在△ABC外部,若BD2=AD2+CD2仍然成立,求∠ADC的度数;
【问题拓展】
(3)如图③,在△ABC中,AB=AC,∠BAC=90°,点D为△ABC外一点.若∠ADC=45°,BD=,CD=,请直接写出AD的长.
答案
答案速查 1 2 3 4 5 6 7 8 9 10
D D C B D D A C D B
11.相等的两个角为对顶角 12.20° 13.15 cm 14.或5
15.证明:连接AC.∵AB=20,BC=15,∠B=90°,
∴由勾股定理,得AC2=202+152=625.
∵CD=7,AD=24,∴CD2+AD2=625,
∴AC2=CD2+AD2,∴∠D=90°,
∴∠A+∠C=360°-180°=180°.
16.解:根据题意得a2+b2=52=25,a·2b=24,
∴a2+b2+2ab=49,∴a+b=7,
由题图②得(a-b)2=25-24=1,
∵a>b,∴a-b=1,
∴a2-b2=(a+b)(a-b)=7×1=7.
17.解:(1)乙船沿南偏东20° 方向航行.
理由如下:由题意得∠APQ=70°,PQ=12×1.5=18(海里),
PR=16×1.5=24(海里),
在△PQR中,∵PQ2+PR2=182+242=900,QR2=302=900,
∴PQ2+PR2=QR2,
∴△PQR是直角三角形,∠QPR=90°,
∴∠BPR=180°-∠APQ-∠QPR=180°-70°-90°=20°,
∴乙船沿南偏东20°方向航行.
(2)能,理由如下:如图,过点C作CD⊥AB于点D,
由题意知∠CPD=60°,PC=2×12=24(海里),
∴∠C=30°,∴PD=PC=12海里,
∴CD==12 ≈20.4(海里).
∵90×=21(海里),21>20.4,
∴他能在14分钟内回到海岸线.
18.(1)证明:①∵△ABC和△DCE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠BCD=∠ACE,∴△CBD≌△CAE,∴BD=AE.
②∵△DCE为等边三角形,∴∠EDC=60°,DE=CD.
∵∠ADC=150°,∴∠ADE=150°-60°=90°,
∴AD2+DE2=AE2.
由①知BD=AE,∴BD2=AD2+CD2.
(2)解:∵△ABC和△DCE都是等边三角形,
∴AC=BC,CD=CE=DE,∠ACB=∠DCE=∠CDE=60°,∴∠BCD=∠ACE,
∴△CBD≌△CAE,∴BD=AE,
∵BD2=AD2+CD2,
∴AE2=AD2+DE2,∴∠ADE=90°,
∴∠ADC=∠ADE-∠CDE=90°-60°=30°.
(3)解:AD的长为3.
点拨:如图,过点A作AE⊥AD,使AE=AD,连接DE,CE,则∠ADE=45°.
∵∠EAD=∠BAC=90°,
∴∠BAD=∠CAE.
又∵AB=AC,AD=AE,
∴△ABD≌△ACE,
∴BD=CE.
∵BD=,
∴CE=.
∵∠ADC=45°,∠ADE=45°,
∴∠CDE=90°,
∵CD=,
∴DE2=CE2-CD2=2-2=18,
在Rt△ADE中,∵∠EAD=90°,∴AE2+AD2=DE2,∴2AD2=18,∴AD=3.
