【期末专项复习】人教版数学八年级上册期末必考真题(含答案)
文档属性
| 名称 | 【期末专项复习】人教版数学八年级上册期末必考真题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 507.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-14 12:54:20 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【期末专项复习】人教版数学八年级上册期末必考真题
阅卷人 一、单选题
得分
1.(2024八上·石家庄期末)已知,关于甲、乙、丙的说法,下列判断正确的是( )
甲:的计算结果为;
乙:当时,;
丙:当时,的值为正数
A.乙错,丙对 B.甲和乙都对 C.甲对,丙错 D.甲错,丙对
2.(2024七下·杭州期末)下列计算正确的是( )
A. B. C. D.
3.(2024八上·北京市期末)已知三角形三边长分别为,若为整数,则这样的三角形个数为( )
A.1个 B.2个 C.3个 D.4个
4.(2024八下·集美期末)将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边在同一条直线上,则∠1的度数为( )
A.75° B.65° C.45° D.30°
5.(2024七下·兴庆期末)如图,在边长为的正方形中,剪去一个边长为a的小正方形,将余下部分对称剪开,拼成一个平行四边形,根据两个图形阴影部分面积的关系,可以得到一个关于x,a的恒等式是( ).
A. B.
C. D.
6.(2022八上·江北期末)如图,在△OAB和△OCD中,,连接AC,BD交于点M,连接OM.下列结论:①;②;③OM平分∠BOC;④MO平分∠BMC.其中正确的是( )
A.①②③ B.①②④ C.①② D.①②③④
7.(2023八上·长春期末)国际数学家大会是数学界的最高水平盛典,大合邀请著名数学粽子者,交流报告数学最新迸展和成果,由承办国的国泉元曾颁发世界数学最高奖——菲尔兹奖.2002年在北京召开了国数学家大会,会标图案是我国古代著名的”赵爽弦图”.图中包合四个面积为24的全等的直角三角形,围成的大正方形面积为100.则直角三角形中较长直角边与较短直角边的长度差为( )
A.2 B.4 C.6 D.8
8.(2024七下·吉州期末)如图,已知AD是的中线,E、F分别是AD和AD延长线上的点,且,连接BF,CE,下列说法中:①;②;③;④.正确的是( )
A.①②③ B.①②④ C.①③④ D.②③④
9.(2024九下·广饶期末模拟)下列运算结果正确的是( )
A. B. C. D.
10.(2024八上·金华期末)如图,等边中,D、E分别为AC、BC边上的点,,连接AE、BD交于点的平分线交于AC边上的点G,BG与AE交于点,连接FG.下列说法:
①;②;③;④AB=AH+FG;
其中正确的说法是( )
A.4个 B.3个 C.2个 D.1个
阅卷人 二、填空题
得分
11.(2024八上·乌鲁木齐期末)将正三角形、正四边形、正五边形按如图所示的位置摆放.如果∠3=32°,那么∠1+∠2= 度.
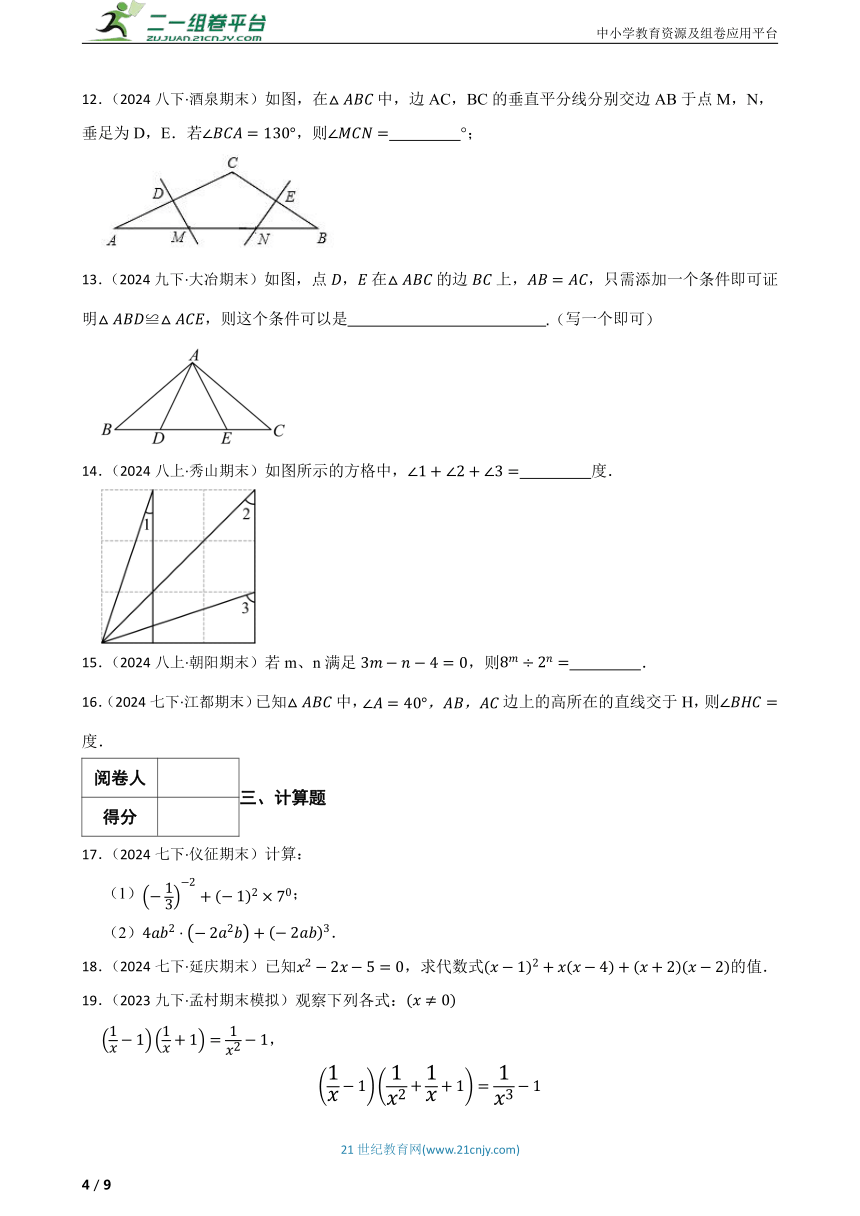
12.(2024八下·酒泉期末)如图,在中,边AC,BC的垂直平分线分别交边AB于点M,N,垂足为D,E.若,则 °;
13.(2024九下·大冶期末)如图,点,在的边上,,只需添加一个条件即可证明≌,则这个条件可以是 写一个即可
14.(2024八上·秀山期末)如图所示的方格中, 度.
15.(2024八上·朝阳期末)若m、n满足,则 .
16.(2024七下·江都期末)已知中,边上的高所在的直线交于H,则 度.
阅卷人 三、计算题
得分
17.(2024七下·仪征期末)计算:
(1);
(2).
18.(2024七下·延庆期末)已知,求代数式的值.
19.(2023九下·孟村期末模拟)观察下列各式:
,
(1)从上面的算式及计算结果,根据你发现的规律直接写下面的空格:________;
(2)用数学的整体思想方法,设,分解因式:,;
(3)已知,a、b、c、d都是正整数,且,化简求的值.
阅卷人 四、解答题
得分
20.(2024八上·昭通期末)如图,小明从点O出发,前进3米后到达点A(米),向右转,再前进3米后到达点B(米),又向右转,……这样小明一直右转了n次刚好回到出发点O处.
根据以上信息,解答下列问题:
(1)n的值为____________.
(2)小明走出的这n边形的周长为____________米.
(3)若一个正m边形的内角和比外角和多,求这个正m边形的每一个内角的度数.
21.(2024八上·碧江期末)(1)解方程:;
(2)若关于x的方程有增根,试求k的值.
22.(2023八上·杭州期末)在△ABC中,为AC边上一点,过点作交ED延长线于点.
(1)求证:.
(2)连结BE,若是AC中点,,求BE的长.
23.如图,在四边形ABCD中,AB∥CD,AC平分∠DAB,AB=2CD,E为AB的中点,连结CE.
(1)求证:四边形AECD为菱形;
(2)若∠D=120°,DC=2,求△ABC的面积
答案解析部分
1.【答案】C
2.【答案】D
3.【答案】C
4.【答案】A
5.【答案】C
6.【答案】B
7.【答案】A
8.【答案】A
9.【答案】B
10.【答案】A
11.【答案】70°.
12.【答案】80
13.【答案】(答案不唯一)
14.【答案】135
15.【答案】16
16.【答案】或.
17.【答案】(1)10
(2)
18.【答案】12
19.【答案】(1);
(2);
(3),
20.【答案】(1)15
(2)45
(3)
21.【答案】(1)
(2)
22.【答案】(1)证明:
(等腰三角形三线合一)
又(对顶角相等)
;
(2)解:过点E作EM⊥BC于M,
.
又,点是AC中点
∵AB=AC,AD⊥BC,
∴BD=CD=8,
又,EM⊥CD
∴BM=8+4=12,
23.【答案】(1)证明:∵E为AB的中点,∴AB=2AE= 2BE.∵AB=2CD,∴CD=AE.
又∵AE∥ CD,∴四边形AECD是平行四边形.
∵AC平分∠DAB,∴∠DAC=∠EAC.∵AB∥CD,∴∠DCA=∠CAB,∴∠DCA=∠DAC,∴AD= CD,∴平行四边形AECD为菱形.
(2)解:∵四边形AECD是菱形,∠D=120°,
∴AD=CD=CE=AE=2,∠D=∠AEC= 120°,
∴AE=CE=BE, ∠CEB= 60°,
∴ ∠CAE= ∠ACE=30°,△CEB是等边三角形,
∴BE=BC=EC=2,∠B=60°,∴∠ACB=90° ,∴AC=,
∴S△ABC=AC·BC=
21世纪教育网(www.21cnjy.com)
9 / 9
【期末专项复习】人教版数学八年级上册期末必考真题
阅卷人 一、单选题
得分
1.(2024八上·石家庄期末)已知,关于甲、乙、丙的说法,下列判断正确的是( )
甲:的计算结果为;
乙:当时,;
丙:当时,的值为正数
A.乙错,丙对 B.甲和乙都对 C.甲对,丙错 D.甲错,丙对
2.(2024七下·杭州期末)下列计算正确的是( )
A. B. C. D.
3.(2024八上·北京市期末)已知三角形三边长分别为,若为整数,则这样的三角形个数为( )
A.1个 B.2个 C.3个 D.4个
4.(2024八下·集美期末)将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边在同一条直线上,则∠1的度数为( )
A.75° B.65° C.45° D.30°
5.(2024七下·兴庆期末)如图,在边长为的正方形中,剪去一个边长为a的小正方形,将余下部分对称剪开,拼成一个平行四边形,根据两个图形阴影部分面积的关系,可以得到一个关于x,a的恒等式是( ).
A. B.
C. D.
6.(2022八上·江北期末)如图,在△OAB和△OCD中,,连接AC,BD交于点M,连接OM.下列结论:①;②;③OM平分∠BOC;④MO平分∠BMC.其中正确的是( )
A.①②③ B.①②④ C.①② D.①②③④
7.(2023八上·长春期末)国际数学家大会是数学界的最高水平盛典,大合邀请著名数学粽子者,交流报告数学最新迸展和成果,由承办国的国泉元曾颁发世界数学最高奖——菲尔兹奖.2002年在北京召开了国数学家大会,会标图案是我国古代著名的”赵爽弦图”.图中包合四个面积为24的全等的直角三角形,围成的大正方形面积为100.则直角三角形中较长直角边与较短直角边的长度差为( )
A.2 B.4 C.6 D.8
8.(2024七下·吉州期末)如图,已知AD是的中线,E、F分别是AD和AD延长线上的点,且,连接BF,CE,下列说法中:①;②;③;④.正确的是( )
A.①②③ B.①②④ C.①③④ D.②③④
9.(2024九下·广饶期末模拟)下列运算结果正确的是( )
A. B. C. D.
10.(2024八上·金华期末)如图,等边中,D、E分别为AC、BC边上的点,,连接AE、BD交于点的平分线交于AC边上的点G,BG与AE交于点,连接FG.下列说法:
①;②;③;④AB=AH+FG;
其中正确的说法是( )
A.4个 B.3个 C.2个 D.1个
阅卷人 二、填空题
得分
11.(2024八上·乌鲁木齐期末)将正三角形、正四边形、正五边形按如图所示的位置摆放.如果∠3=32°,那么∠1+∠2= 度.
12.(2024八下·酒泉期末)如图,在中,边AC,BC的垂直平分线分别交边AB于点M,N,垂足为D,E.若,则 °;
13.(2024九下·大冶期末)如图,点,在的边上,,只需添加一个条件即可证明≌,则这个条件可以是 写一个即可
14.(2024八上·秀山期末)如图所示的方格中, 度.
15.(2024八上·朝阳期末)若m、n满足,则 .
16.(2024七下·江都期末)已知中,边上的高所在的直线交于H,则 度.
阅卷人 三、计算题
得分
17.(2024七下·仪征期末)计算:
(1);
(2).
18.(2024七下·延庆期末)已知,求代数式的值.
19.(2023九下·孟村期末模拟)观察下列各式:
,
(1)从上面的算式及计算结果,根据你发现的规律直接写下面的空格:________;
(2)用数学的整体思想方法,设,分解因式:,;
(3)已知,a、b、c、d都是正整数,且,化简求的值.
阅卷人 四、解答题
得分
20.(2024八上·昭通期末)如图,小明从点O出发,前进3米后到达点A(米),向右转,再前进3米后到达点B(米),又向右转,……这样小明一直右转了n次刚好回到出发点O处.
根据以上信息,解答下列问题:
(1)n的值为____________.
(2)小明走出的这n边形的周长为____________米.
(3)若一个正m边形的内角和比外角和多,求这个正m边形的每一个内角的度数.
21.(2024八上·碧江期末)(1)解方程:;
(2)若关于x的方程有增根,试求k的值.
22.(2023八上·杭州期末)在△ABC中,为AC边上一点,过点作交ED延长线于点.
(1)求证:.
(2)连结BE,若是AC中点,,求BE的长.
23.如图,在四边形ABCD中,AB∥CD,AC平分∠DAB,AB=2CD,E为AB的中点,连结CE.
(1)求证:四边形AECD为菱形;
(2)若∠D=120°,DC=2,求△ABC的面积
答案解析部分
1.【答案】C
2.【答案】D
3.【答案】C
4.【答案】A
5.【答案】C
6.【答案】B
7.【答案】A
8.【答案】A
9.【答案】B
10.【答案】A
11.【答案】70°.
12.【答案】80
13.【答案】(答案不唯一)
14.【答案】135
15.【答案】16
16.【答案】或.
17.【答案】(1)10
(2)
18.【答案】12
19.【答案】(1);
(2);
(3),
20.【答案】(1)15
(2)45
(3)
21.【答案】(1)
(2)
22.【答案】(1)证明:
(等腰三角形三线合一)
又(对顶角相等)
;
(2)解:过点E作EM⊥BC于M,
.
又,点是AC中点
∵AB=AC,AD⊥BC,
∴BD=CD=8,
又,EM⊥CD
∴BM=8+4=12,
23.【答案】(1)证明:∵E为AB的中点,∴AB=2AE= 2BE.∵AB=2CD,∴CD=AE.
又∵AE∥ CD,∴四边形AECD是平行四边形.
∵AC平分∠DAB,∴∠DAC=∠EAC.∵AB∥CD,∴∠DCA=∠CAB,∴∠DCA=∠DAC,∴AD= CD,∴平行四边形AECD为菱形.
(2)解:∵四边形AECD是菱形,∠D=120°,
∴AD=CD=CE=AE=2,∠D=∠AEC= 120°,
∴AE=CE=BE, ∠CEB= 60°,
∴ ∠CAE= ∠ACE=30°,△CEB是等边三角形,
∴BE=BC=EC=2,∠B=60°,∴∠ACB=90° ,∴AC=,
∴S△ABC=AC·BC=
21世纪教育网(www.21cnjy.com)
9 / 9
同课章节目录
