1.1.2 正弦和余弦 课件(共20张PPT)2024-2025学年数学北师大版九年级下册
文档属性
| 名称 | 1.1.2 正弦和余弦 课件(共20张PPT)2024-2025学年数学北师大版九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 637.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-13 21:10:12 | ||
图片预览


文档简介
(共20张PPT)
第一章 直角三角形的
边角关系
1 锐角三角函数
第2课时 正弦和余弦
北师大版-数学-九年级下册
学习目标
1.能利用相似的直角三角形,探索并认识锐角三角函数——正弦、余弦,理解锐角的正弦与余弦和梯子倾斜程度的关系.
2.能够用sinA,cosA表示直角三角形中直角边与斜边的比,能够用正弦、余弦进行简单的计算.
【重点】理解正弦与余弦的概念
【难点】能用正弦、余弦的知识,根据三角形中已知的边和角求出未知的边和角
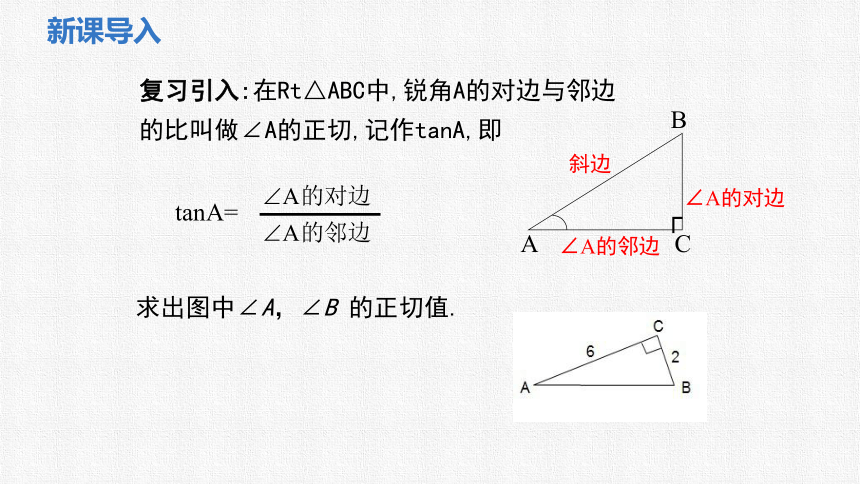
新课导入
复习引入:在Rt△ABC中,锐角A的对边与邻边的比叫做∠A的正切,记作tanA,即
tanA=
A
B
C
∠A的对边
∠A的邻边
┌
斜边
求出图中∠A,∠B 的正切值.
新知探究
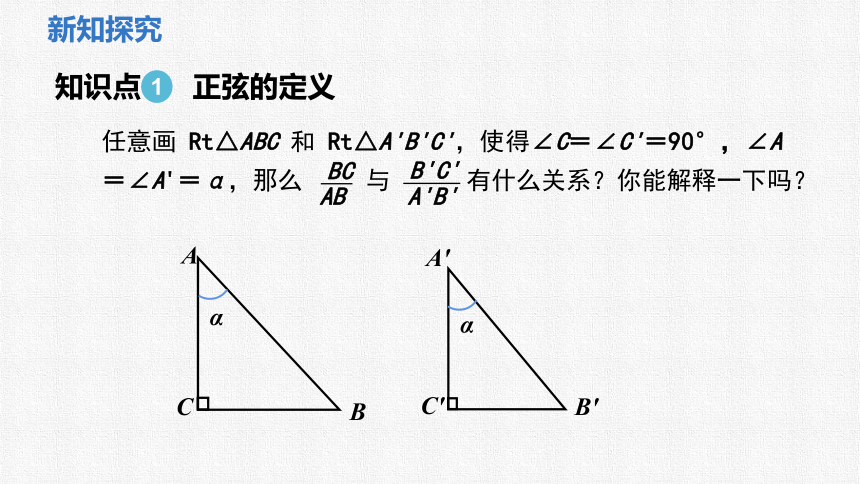
知识点 正弦的定义
1
任意画 Rt△ABC 和 Rt△A'B'C',使得∠C=∠C'=90°,∠A=∠A'=α,那么 与 有什么关系?你能解释一下吗?
AB
BC
A'B'
B'C'
A
B
C
α
A'
B'
C'
α
新知探究
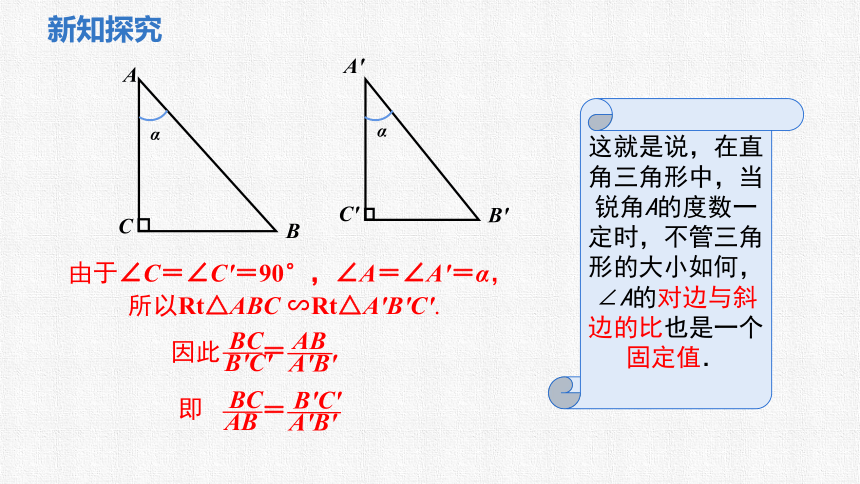
由于∠C=∠C'=90°,∠A=∠A'=α,
A
B
C
α
A'
B'
C'
α
所以Rt△ABC ∽Rt△A'B'C'.
因此
B'C'
BC
A'B'
AB
=
AB
BC
A'B'
B'C'
=
即
这就是说,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比也是一个固定值.
新知探究
B
A
C
c
a
b
斜边
对边
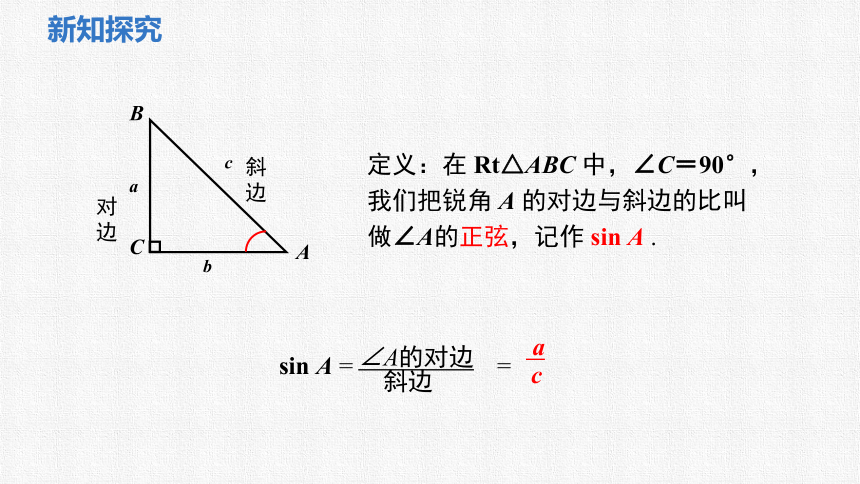
定义:在 Rt△ABC 中,∠C=90°,我们把锐角 A 的对边与斜边的比叫做∠A的正弦,记作 sin A .
∠A的对边
斜边
sin A = =
c
a
新知探究
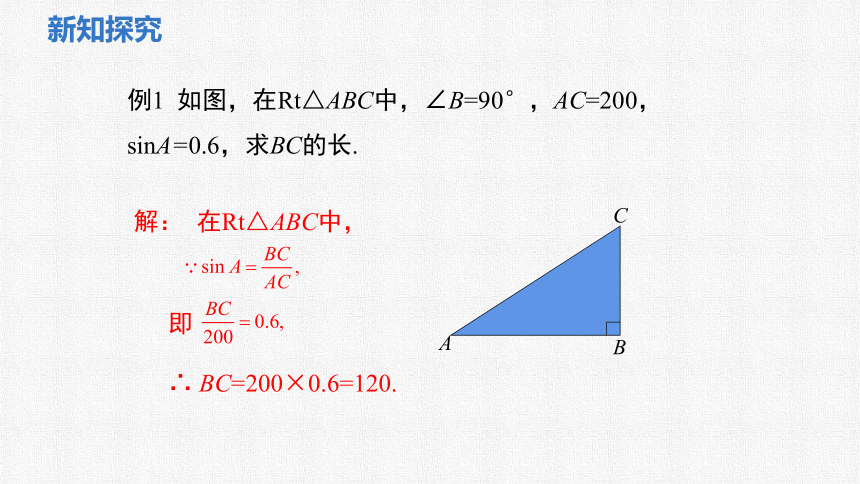
解: 在Rt△ABC中,
即
∴ BC=200×0.6=120.
A
B
C
例1 如图,在Rt△ABC中,∠B=90°,AC=200,sinA=0.6,求BC的长.
新知探究
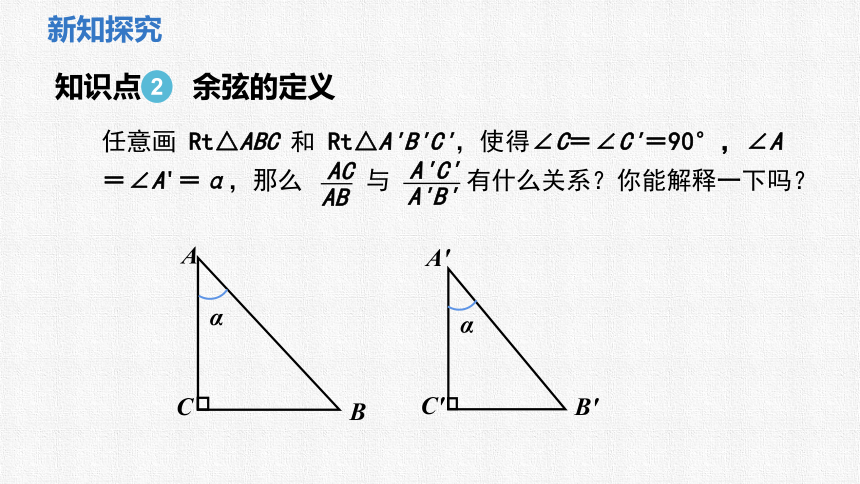
知识点 余弦的定义
2
任意画 Rt△ABC 和 Rt△A'B'C',使得∠C=∠C'=90°,∠A=∠A'=α,那么 与 有什么关系?你能解释一下吗?
AB
AC
A'B'
A'C'
A
B
C
α
A'
B'
C'
α
新知探究
A
B
C
α
A'
B'
C'
α
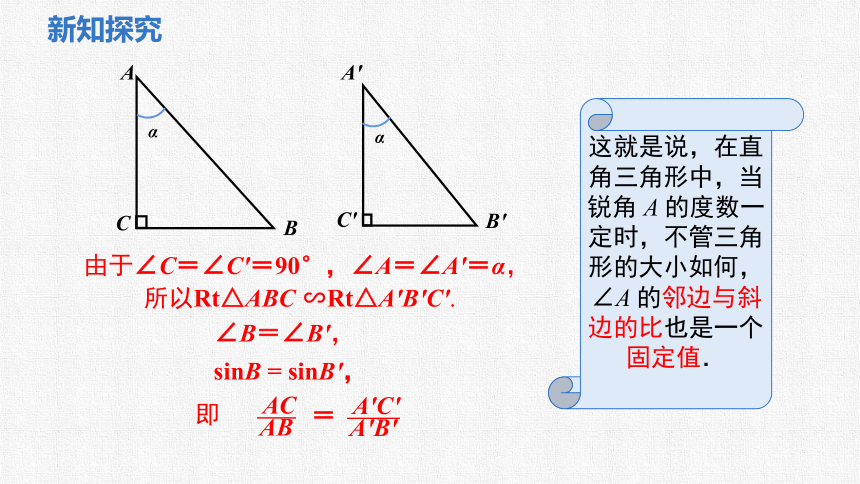
由于∠C=∠C'=90°,∠A=∠A'=α,
所以Rt△ABC ∽Rt△A'B'C'.
∠B=∠B',
sinB = sinB',
AB
AC
A'B'
A'C'
=
即
这就是说,在直角三角形中,当锐角 A 的度数一定时,不管三角形的大小如何,∠A 的邻边与斜边的比也是一个固定值.
新知探究
三角函数的定义:锐角 A 的正弦、余弦和正切都是∠A 的三角函数(trigonometric function).当锐角 A 变化时,相应的正弦、余弦和正切值也随之变化.
如图,梯子的倾斜程度与 sinA 和 cosA 有关系吗?
sinA的值越大,梯子越 ____ ;
cosA的值越 ____ ,梯子越陡.
陡
小
新知探究
定义中应该注意的几个问题:
1.sinA,cosA是在直角三角形中定义的,∠A是锐角(做题时注意数形结合,没有直角三角形时要构造直角三角形).
2.sinA,cosA是一个完整的符号,分别表示∠A的正弦,余弦 (习惯省去“∠”符号).
3.sinA,cosA 是一个比值,是直角边与斜边之比,注意比的顺序.
4.sinA,cosA的大小只与∠A的大小有关,而与直角三角形的边长无关.
5.角相等,则其三角函数值相等;两锐角的三角函数值相等,则这两个锐角相等.
6.锐角A的正弦、余弦和正切都是∠A的三角函数.
新知探究
知识点 正弦、余弦之间简单的关系
3
例2 如图,在Rt△ABC中,∠C=90°, AC=10, 求AB, sinB.
你发现了什么?
在直角三角形中,一个锐角的正弦等于另一个锐角的余弦.
A
B
C
锐角三角函数之间的关系:
(1)同一个角:①商的关系:tanA= ;②平方关系:sin2A+cos2A=1.
(2)互余两角:若∠A+∠B=90°,则sinA=cosB
=cos(90°-A),cosA=sinB=sin(90°-A).
tanA·tanB=1
新知探究
拓展了解
大家可以选择感兴趣的结论课下自己尝试证明
课堂小结
正弦和余弦
正弦
B
A
C
c
a
b
斜边
对边
∠A的对边
斜边
sin A = =
c
a
余弦
B
A
C
c
a
b
斜边
邻边
∠A的邻边
斜边
cos A = =
c
b
锐角三角函数
正弦、余弦和正切的相互转化
课堂训练
1. 如图,在△ABC中,∠C=90°,AB=13,BC=5,则sin A的值是( )
A. B. C. D.
A
C
B
A
2.在Rt△ABC中,∠C=90°,若AC=2BC,则sin A的值是( )
A. B. 2 C. D.
C
课堂训练
3.已知在Rt△ABC中,∠C=90°,AB=7,BC=5, 那么下列式子中正确的是( )
A.sinA=
B.cosA=
C.tanA=
D.tanA=
A
课堂训练
4.△ABC在正方形网格中的位置如图所示,则cosα的值是( )
A.
B.
C.
D.
C
课堂训练
5.在△ABC中,∠C=90 °, ,BC=20,
求△ABC的周长和面积.
A
B
C
解:在Rt △ABC中,
由勾股定理可得:AC=15,
∴S△ABC =15×20÷2=150,
C△ABC =20+25+15=60.
课堂训练
6.如图,在正方形 ABCD 中,M 是 AD 的中点,BE = 3AE,求 sin∠ECM.
解:设正方形ABCD的边长为 4x,
∵M 是 AD 的中点,BE = 3AE,
∴ AM = DM = 2x,AE = x,
BE = 3x.由勾股定理可知,
A
M
E
D
B
C
课堂训练
6.如图,在正方形 ABCD 中,M 是 AD 的中点,BE = 3AE,求 sin∠ECM.
A
M
E
D
B
C
由勾股定理逆定理可知,△EMC 为直角三角形.
第一章 直角三角形的
边角关系
1 锐角三角函数
第2课时 正弦和余弦
北师大版-数学-九年级下册
学习目标
1.能利用相似的直角三角形,探索并认识锐角三角函数——正弦、余弦,理解锐角的正弦与余弦和梯子倾斜程度的关系.
2.能够用sinA,cosA表示直角三角形中直角边与斜边的比,能够用正弦、余弦进行简单的计算.
【重点】理解正弦与余弦的概念
【难点】能用正弦、余弦的知识,根据三角形中已知的边和角求出未知的边和角
新课导入
复习引入:在Rt△ABC中,锐角A的对边与邻边的比叫做∠A的正切,记作tanA,即
tanA=
A
B
C
∠A的对边
∠A的邻边
┌
斜边
求出图中∠A,∠B 的正切值.
新知探究
知识点 正弦的定义
1
任意画 Rt△ABC 和 Rt△A'B'C',使得∠C=∠C'=90°,∠A=∠A'=α,那么 与 有什么关系?你能解释一下吗?
AB
BC
A'B'
B'C'
A
B
C
α
A'
B'
C'
α
新知探究
由于∠C=∠C'=90°,∠A=∠A'=α,
A
B
C
α
A'
B'
C'
α
所以Rt△ABC ∽Rt△A'B'C'.
因此
B'C'
BC
A'B'
AB
=
AB
BC
A'B'
B'C'
=
即
这就是说,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比也是一个固定值.
新知探究
B
A
C
c
a
b
斜边
对边
定义:在 Rt△ABC 中,∠C=90°,我们把锐角 A 的对边与斜边的比叫做∠A的正弦,记作 sin A .
∠A的对边
斜边
sin A = =
c
a
新知探究
解: 在Rt△ABC中,
即
∴ BC=200×0.6=120.
A
B
C
例1 如图,在Rt△ABC中,∠B=90°,AC=200,sinA=0.6,求BC的长.
新知探究
知识点 余弦的定义
2
任意画 Rt△ABC 和 Rt△A'B'C',使得∠C=∠C'=90°,∠A=∠A'=α,那么 与 有什么关系?你能解释一下吗?
AB
AC
A'B'
A'C'
A
B
C
α
A'
B'
C'
α
新知探究
A
B
C
α
A'
B'
C'
α
由于∠C=∠C'=90°,∠A=∠A'=α,
所以Rt△ABC ∽Rt△A'B'C'.
∠B=∠B',
sinB = sinB',
AB
AC
A'B'
A'C'
=
即
这就是说,在直角三角形中,当锐角 A 的度数一定时,不管三角形的大小如何,∠A 的邻边与斜边的比也是一个固定值.
新知探究
三角函数的定义:锐角 A 的正弦、余弦和正切都是∠A 的三角函数(trigonometric function).当锐角 A 变化时,相应的正弦、余弦和正切值也随之变化.
如图,梯子的倾斜程度与 sinA 和 cosA 有关系吗?
sinA的值越大,梯子越 ____ ;
cosA的值越 ____ ,梯子越陡.
陡
小
新知探究
定义中应该注意的几个问题:
1.sinA,cosA是在直角三角形中定义的,∠A是锐角(做题时注意数形结合,没有直角三角形时要构造直角三角形).
2.sinA,cosA是一个完整的符号,分别表示∠A的正弦,余弦 (习惯省去“∠”符号).
3.sinA,cosA 是一个比值,是直角边与斜边之比,注意比的顺序.
4.sinA,cosA的大小只与∠A的大小有关,而与直角三角形的边长无关.
5.角相等,则其三角函数值相等;两锐角的三角函数值相等,则这两个锐角相等.
6.锐角A的正弦、余弦和正切都是∠A的三角函数.
新知探究
知识点 正弦、余弦之间简单的关系
3
例2 如图,在Rt△ABC中,∠C=90°, AC=10, 求AB, sinB.
你发现了什么?
在直角三角形中,一个锐角的正弦等于另一个锐角的余弦.
A
B
C
锐角三角函数之间的关系:
(1)同一个角:①商的关系:tanA= ;②平方关系:sin2A+cos2A=1.
(2)互余两角:若∠A+∠B=90°,则sinA=cosB
=cos(90°-A),cosA=sinB=sin(90°-A).
tanA·tanB=1
新知探究
拓展了解
大家可以选择感兴趣的结论课下自己尝试证明
课堂小结
正弦和余弦
正弦
B
A
C
c
a
b
斜边
对边
∠A的对边
斜边
sin A = =
c
a
余弦
B
A
C
c
a
b
斜边
邻边
∠A的邻边
斜边
cos A = =
c
b
锐角三角函数
正弦、余弦和正切的相互转化
课堂训练
1. 如图,在△ABC中,∠C=90°,AB=13,BC=5,则sin A的值是( )
A. B. C. D.
A
C
B
A
2.在Rt△ABC中,∠C=90°,若AC=2BC,则sin A的值是( )
A. B. 2 C. D.
C
课堂训练
3.已知在Rt△ABC中,∠C=90°,AB=7,BC=5, 那么下列式子中正确的是( )
A.sinA=
B.cosA=
C.tanA=
D.tanA=
A
课堂训练
4.△ABC在正方形网格中的位置如图所示,则cosα的值是( )
A.
B.
C.
D.
C
课堂训练
5.在△ABC中,∠C=90 °, ,BC=20,
求△ABC的周长和面积.
A
B
C
解:在Rt △ABC中,
由勾股定理可得:AC=15,
∴S△ABC =15×20÷2=150,
C△ABC =20+25+15=60.
课堂训练
6.如图,在正方形 ABCD 中,M 是 AD 的中点,BE = 3AE,求 sin∠ECM.
解:设正方形ABCD的边长为 4x,
∵M 是 AD 的中点,BE = 3AE,
∴ AM = DM = 2x,AE = x,
BE = 3x.由勾股定理可知,
A
M
E
D
B
C
课堂训练
6.如图,在正方形 ABCD 中,M 是 AD 的中点,BE = 3AE,求 sin∠ECM.
A
M
E
D
B
C
由勾股定理逆定理可知,△EMC 为直角三角形.
