1.6 利用三角函数测高 课件(共24张PPT)2024-2025学年数学北师大版九年级下册
文档属性
| 名称 | 1.6 利用三角函数测高 课件(共24张PPT)2024-2025学年数学北师大版九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 15.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-13 21:13:59 | ||
图片预览





文档简介
(共24张PPT)
第一章 直角三角形的
边角关系
6 利用三角函数测高
北师大版-数学-九年级下册
学习目标
1.了解测倾器的构造及使用方法,会设计简单的活动方案;
2.掌握测量底部可以到达的物体高度的方法;
3.掌握测量底部不可以到达的物体高度的方法.
【重点】经历运用仪器进行实地测量以及撰写活动报告的过程,
能够对所得到的数据进行分析.
【难点】能综合应用直角三角形的边角关系的知识解决实际问题.
新课导入
看一看:下图为高度世界排名前三的建筑,我们应该如何准确测出它们的实际高度呢?
哈利法塔高828米,楼层总数162层
默迪卡118大楼共118层,楼高678.90米
上海中心大厦地上127层,建筑高度632米
新知探究
知识点 测量倾斜角
1
测量倾斜角可以用测倾器.
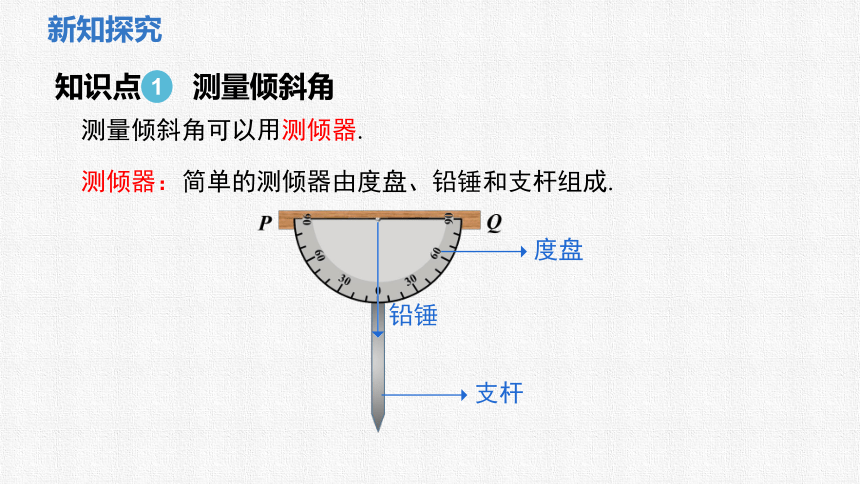
测倾器:简单的测倾器由度盘、铅锤和支杆组成.
度盘
铅锤
支杆
新知探究
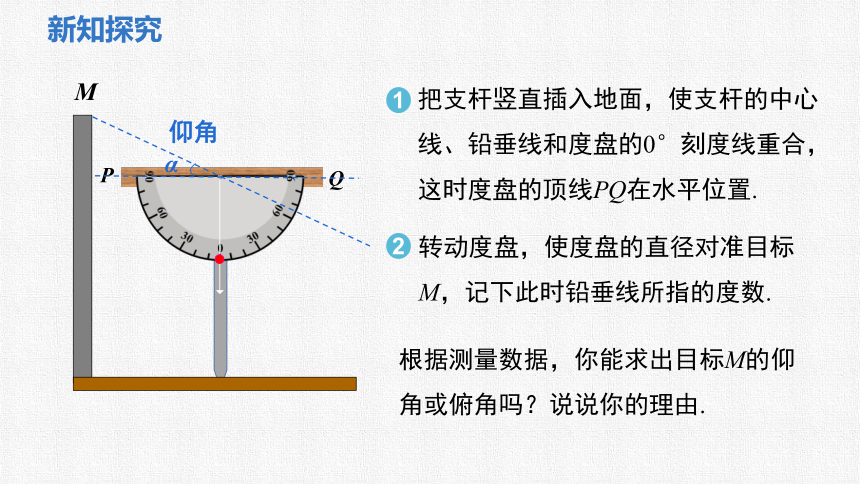
把支杆竖直插入地面,使支杆的中心线、铅垂线和度盘的0°刻度线重合,这时度盘的顶线PQ在水平位置.
转动度盘,使度盘的直径对准目标M,记下此时铅垂线所指的度数.
M
P
Q
α
仰角
根据测量数据,你能求出目标M的仰角或俯角吗?说说你的理由.
1
2
新知探究
M
P
Q
α
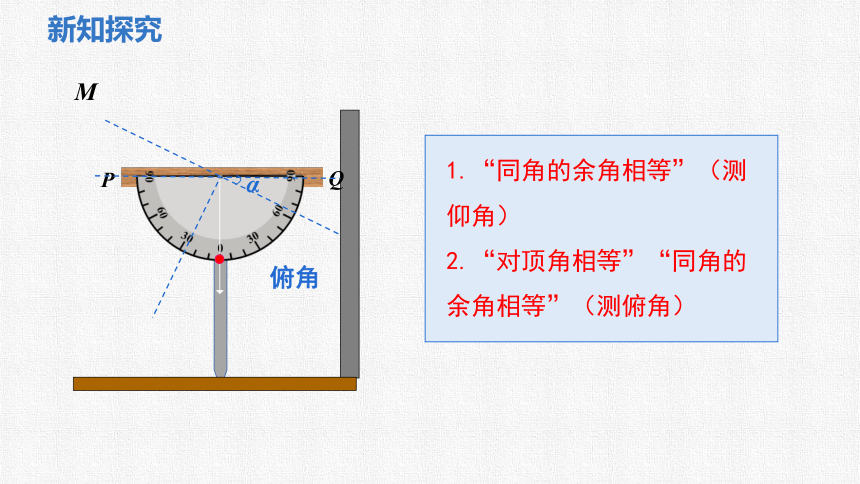
俯角
1.“同角的余角相等”(测仰角)
2.“对顶角相等”“同角的余角相等”(测俯角)
新知探究
知识点 测量底部可以到达的物体的高度
2
所谓“底部可以到达” ,就是在地面上可以无障碍地直接测得测点与被测物体的底部之间的距离.
如图,要测量物体MN的高度,可按下列步骤进行:
M
N
新知探究
M
N
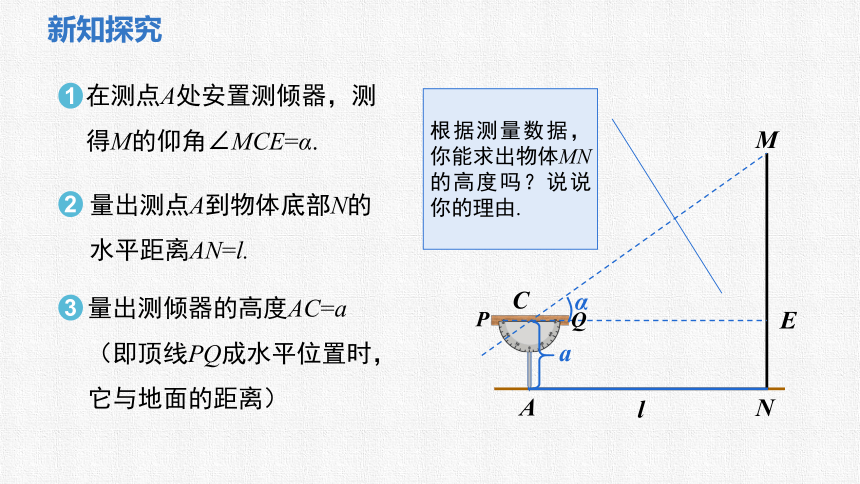
在测点A处安置测倾器,测得M的仰角∠MCE=α.
A
α
C
量出测点A到物体底部N的水平距离AN=l.
l
量出测倾器的高度AC=a
(即顶线PQ成水平位置时,它与地面的距离)
a
3
2
1
P
Q
根据测量数据,你能求出物体MN的高度吗?说说你的理由.
E
新知探究
M
N
A
α
C
l
a
可求出MN的高度:
MN=ME+EN=l·tanα+a.
E
新知探究
例1:如图,某中学在主楼的顶部和大门的上方之间挂一些彩旗.经测量,得到大门的高度是5m,大门距主楼的距离是30m,在大门处测得主楼顶部的仰角是30°,而当时侧倾器离地面1.4m,求学校主楼的高度(精确到0.01m).
C
A
B
E
D
30°
新知探究
C
A
B
E
D
30°
解:如图,作EM垂直CD于M点.
∠DEM=30°,
M
根据题意,可知
CM=BE=1.4m
BC=EM=30m,
在Rt△DEM中,
DM=EMtan30°≈30×0.577 =17.32(m),
CD=DM+CM=17.32+1.4≈18.72(m).
∴学校主楼的高度约为18.72m.
新知探究
知识点 测量底部不可以到达的物体的高度
3
所谓“底部不可以到达” ,就是在地面上不能直接测得测点与被测物体的底部之间的距离.
如图,要测量物体MN的高度,可以按下列步骤进行:
M
N
新知探究
在测点A处安置测倾器,测得M的仰角∠MCE=α.
在测点A与物体之间B处安置测倾器,测得此时M的仰角∠MDE=β.
量出测倾器的高度AC=BD=a,
以及测点A,B之间的距离AB=b.
3
2
1
根据测量数据,你能求出物体MN的高度吗?说说你的理由.
M
N
A
α
C
B
D
β
a
E
b
新知探究
M
N
A
α
C
E
B
D
β
a
b
CD=AB=CE-DE
=
∴ME=
∴MN=
可求出MN的高度:
= b
课题 在平面上测量某底部不可到达的大厦的高AB 测量示意图 测得数据 (测倾器高度为1m) 测量项目 ∠α ∠β CD的长
第一次 30° 16' 45° 35' 60.11m
第二次 29° 44' 44° 25’' 59.89m
平均值
新知探究
例2:下表是小明所填实习报告的部分内容,请根据数据求大楼的高.
C
E
D
F
A
G
B
α
β
30°
45°
60m
新知探究
C
E
D
F
A
G
B
α
β
解:由表格中数据,得α=30°,β=45°,
答:大楼高度为 .
∵
∵
∵
课堂小结
利用三角函数测高
测倾器的认识及使用
测量底部可以到达的物体的高度(一次测量仰角)
测量底部不可以到达的物体的高度(两次测量仰角)
利用解三角形的知识,求出物体的高度
课堂训练
1. 如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端30 m的B处测得树顶点A的仰角∠ABO为∠α,则树OA的高度为( )
A. m B.30sinα m
C.30tanα m D.30cosα m
C
课堂训练
2.如图,山顶有一座电视塔,在地面上一点A处测得塔顶B处的仰角α=60°,在塔底C处测得点A的俯角β=45°,已知塔高60米,则山高CD等于( )
A.30(1+ )米
B.30( -1)米
C.30 米
D.(30 +1)米
A
课堂训练
5.4
3.如图,一幢大楼的顶部竖有一块写有校训的宣传牌CD.小明在山坡的底部A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB垂直于视线AD,AB=20米,AE=30米,则这块宣传牌CD的高度约为_______米.(测倾器的高度忽略不计,结果精确到0.1米,参考数据: ≈1.414, ≈1.732)
课堂训练
4.在学习完“利用三角函数测高”这节内容之后,某兴趣小组开展了测量学校旗杆高度的实践活动.如图,在测点A处安置测倾器,量出高度AB=1.5 m,测得旗杆顶端D的仰角∠DBE=32°,量出测点A到旗杆底部C的水平距离AC=20 m,根据测量数据,求旗杆CD的高度.(结果精确到0.1 m,参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)
课堂训练
答:旗杆CD的高度约13.9米.
解:由题意得AC=20米,
AB=1.5米,
∵∠DBE=32°,
∴DE=BE·tan32°≈20×0.62=12.4(米),
∴CD=DE+CE=DE+AB=12.4+1.5=13.9(米).
课堂训练
5.数学兴趣小组到黄河风景名胜区测量炎帝塑像(塑像中高者)的高度,如图所示,炎帝塑像DE在高55m的小山EC上,在A处测得塑像底部E的仰角为34°,再沿AC方向前进21m到达B处,测得塑像顶部D的仰角为60°求炎帝塑像DE的高度.(精确到1m.参考数据:sin34°≈0.56,
cos34°≈0.83,tan34°≈0.67,≈1.73)
课堂训练
解:∵∠ACE=90°,∠CAE=34°,CE=55m,∴tan∠CAE=
∴AC= = 82.1m.∵AB=21m,∴BC=AC-AB=61.1m,
在Rt△BCD中,tan60°= =∴CD=BC ≈1.73×61.1≈105.7m,∴DE=CD-EC=105.7-55≈51m.
答:炎帝塑像DE的高度约为51m.
第一章 直角三角形的
边角关系
6 利用三角函数测高
北师大版-数学-九年级下册
学习目标
1.了解测倾器的构造及使用方法,会设计简单的活动方案;
2.掌握测量底部可以到达的物体高度的方法;
3.掌握测量底部不可以到达的物体高度的方法.
【重点】经历运用仪器进行实地测量以及撰写活动报告的过程,
能够对所得到的数据进行分析.
【难点】能综合应用直角三角形的边角关系的知识解决实际问题.
新课导入
看一看:下图为高度世界排名前三的建筑,我们应该如何准确测出它们的实际高度呢?
哈利法塔高828米,楼层总数162层
默迪卡118大楼共118层,楼高678.90米
上海中心大厦地上127层,建筑高度632米
新知探究
知识点 测量倾斜角
1
测量倾斜角可以用测倾器.
测倾器:简单的测倾器由度盘、铅锤和支杆组成.
度盘
铅锤
支杆
新知探究
把支杆竖直插入地面,使支杆的中心线、铅垂线和度盘的0°刻度线重合,这时度盘的顶线PQ在水平位置.
转动度盘,使度盘的直径对准目标M,记下此时铅垂线所指的度数.
M
P
Q
α
仰角
根据测量数据,你能求出目标M的仰角或俯角吗?说说你的理由.
1
2
新知探究
M
P
Q
α
俯角
1.“同角的余角相等”(测仰角)
2.“对顶角相等”“同角的余角相等”(测俯角)
新知探究
知识点 测量底部可以到达的物体的高度
2
所谓“底部可以到达” ,就是在地面上可以无障碍地直接测得测点与被测物体的底部之间的距离.
如图,要测量物体MN的高度,可按下列步骤进行:
M
N
新知探究
M
N
在测点A处安置测倾器,测得M的仰角∠MCE=α.
A
α
C
量出测点A到物体底部N的水平距离AN=l.
l
量出测倾器的高度AC=a
(即顶线PQ成水平位置时,它与地面的距离)
a
3
2
1
P
Q
根据测量数据,你能求出物体MN的高度吗?说说你的理由.
E
新知探究
M
N
A
α
C
l
a
可求出MN的高度:
MN=ME+EN=l·tanα+a.
E
新知探究
例1:如图,某中学在主楼的顶部和大门的上方之间挂一些彩旗.经测量,得到大门的高度是5m,大门距主楼的距离是30m,在大门处测得主楼顶部的仰角是30°,而当时侧倾器离地面1.4m,求学校主楼的高度(精确到0.01m).
C
A
B
E
D
30°
新知探究
C
A
B
E
D
30°
解:如图,作EM垂直CD于M点.
∠DEM=30°,
M
根据题意,可知
CM=BE=1.4m
BC=EM=30m,
在Rt△DEM中,
DM=EMtan30°≈30×0.577 =17.32(m),
CD=DM+CM=17.32+1.4≈18.72(m).
∴学校主楼的高度约为18.72m.
新知探究
知识点 测量底部不可以到达的物体的高度
3
所谓“底部不可以到达” ,就是在地面上不能直接测得测点与被测物体的底部之间的距离.
如图,要测量物体MN的高度,可以按下列步骤进行:
M
N
新知探究
在测点A处安置测倾器,测得M的仰角∠MCE=α.
在测点A与物体之间B处安置测倾器,测得此时M的仰角∠MDE=β.
量出测倾器的高度AC=BD=a,
以及测点A,B之间的距离AB=b.
3
2
1
根据测量数据,你能求出物体MN的高度吗?说说你的理由.
M
N
A
α
C
B
D
β
a
E
b
新知探究
M
N
A
α
C
E
B
D
β
a
b
CD=AB=CE-DE
=
∴ME=
∴MN=
可求出MN的高度:
= b
课题 在平面上测量某底部不可到达的大厦的高AB 测量示意图 测得数据 (测倾器高度为1m) 测量项目 ∠α ∠β CD的长
第一次 30° 16' 45° 35' 60.11m
第二次 29° 44' 44° 25’' 59.89m
平均值
新知探究
例2:下表是小明所填实习报告的部分内容,请根据数据求大楼的高.
C
E
D
F
A
G
B
α
β
30°
45°
60m
新知探究
C
E
D
F
A
G
B
α
β
解:由表格中数据,得α=30°,β=45°,
答:大楼高度为 .
∵
∵
∵
课堂小结
利用三角函数测高
测倾器的认识及使用
测量底部可以到达的物体的高度(一次测量仰角)
测量底部不可以到达的物体的高度(两次测量仰角)
利用解三角形的知识,求出物体的高度
课堂训练
1. 如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端30 m的B处测得树顶点A的仰角∠ABO为∠α,则树OA的高度为( )
A. m B.30sinα m
C.30tanα m D.30cosα m
C
课堂训练
2.如图,山顶有一座电视塔,在地面上一点A处测得塔顶B处的仰角α=60°,在塔底C处测得点A的俯角β=45°,已知塔高60米,则山高CD等于( )
A.30(1+ )米
B.30( -1)米
C.30 米
D.(30 +1)米
A
课堂训练
5.4
3.如图,一幢大楼的顶部竖有一块写有校训的宣传牌CD.小明在山坡的底部A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB垂直于视线AD,AB=20米,AE=30米,则这块宣传牌CD的高度约为_______米.(测倾器的高度忽略不计,结果精确到0.1米,参考数据: ≈1.414, ≈1.732)
课堂训练
4.在学习完“利用三角函数测高”这节内容之后,某兴趣小组开展了测量学校旗杆高度的实践活动.如图,在测点A处安置测倾器,量出高度AB=1.5 m,测得旗杆顶端D的仰角∠DBE=32°,量出测点A到旗杆底部C的水平距离AC=20 m,根据测量数据,求旗杆CD的高度.(结果精确到0.1 m,参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)
课堂训练
答:旗杆CD的高度约13.9米.
解:由题意得AC=20米,
AB=1.5米,
∵∠DBE=32°,
∴DE=BE·tan32°≈20×0.62=12.4(米),
∴CD=DE+CE=DE+AB=12.4+1.5=13.9(米).
课堂训练
5.数学兴趣小组到黄河风景名胜区测量炎帝塑像(塑像中高者)的高度,如图所示,炎帝塑像DE在高55m的小山EC上,在A处测得塑像底部E的仰角为34°,再沿AC方向前进21m到达B处,测得塑像顶部D的仰角为60°求炎帝塑像DE的高度.(精确到1m.参考数据:sin34°≈0.56,
cos34°≈0.83,tan34°≈0.67,≈1.73)
课堂训练
解:∵∠ACE=90°,∠CAE=34°,CE=55m,∴tan∠CAE=
∴AC= = 82.1m.∵AB=21m,∴BC=AC-AB=61.1m,
在Rt△BCD中,tan60°= =∴CD=BC ≈1.73×61.1≈105.7m,∴DE=CD-EC=105.7-55≈51m.
答:炎帝塑像DE的高度约为51m.
