2.2.2二次函数y =a x2 和 y =ax2+c的图象与性质 课件 (共24张PPT)2024-2025学年数学北师大版九年级下册
文档属性
| 名称 | 2.2.2二次函数y =a x2 和 y =ax2+c的图象与性质 课件 (共24张PPT)2024-2025学年数学北师大版九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 830.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-13 21:14:24 | ||
图片预览


文档简介
(共24张PPT)
第二章 二次函数
2 二次函数的图象与性质
北师大版-数学-九年级下册
第2课时 二次函数y =ax2 和 y =ax2+c的图象与性质
学习目标
【重点】会画y=ax2和y=ax2+c(a≠0)的图象,掌握两者之间的联系.
【难点】灵活运用y=ax2和y=ax2+c(a≠0)的图象,体会数与形的相互联系.
1.会画二次函数y=ax2和y=ax2+c(a≠0)的图象.
2.掌握二次函数y=ax2与y=ax2+c(a≠0)图象之间的联系.
3.能灵活运用二次函数y=ax2和y=ax2+c(a≠0)的知识解决问题.
新课导入
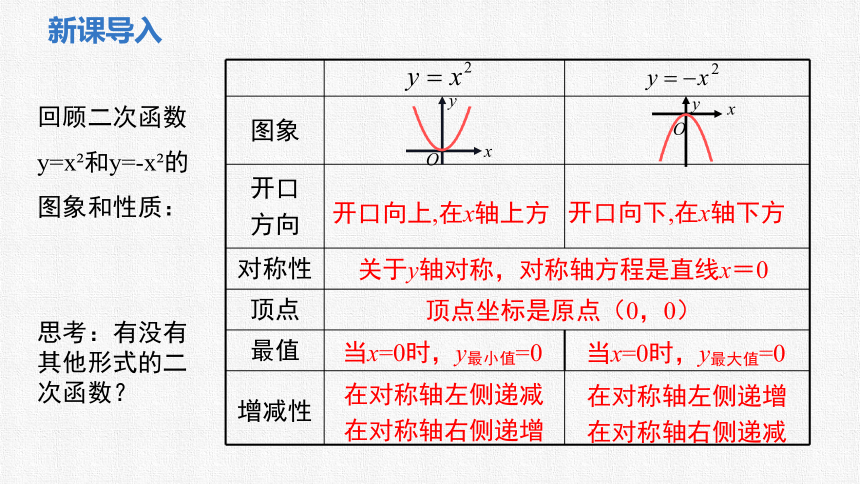
回顾二次函数
y=x 和y=-x 的
图象和性质:
图象
开口 方向
对称性 顶点 最值
增减性
开口向上,在x轴上方
开口向下,在x轴下方
关于y轴对称,对称轴方程是直线x=0
顶点坐标是原点(0,0)
当x=0时,y最小值=0
当x=0时,y最大值=0
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
y
O
x
y
O
x
思考:有没有其他形式的二次函数?
新知探究
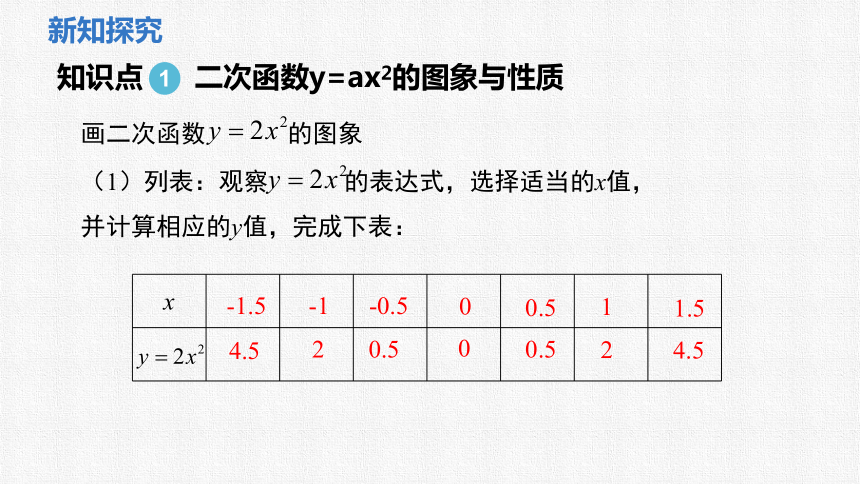
画二次函数 的图象
(1)列表:观察 的表达式,选择适当的x值, 并计算相应的y值,完成下表:
知识点 二次函数y=ax2的图象与性质
1
x
4.5
2
0.5
0
0
0.5
0.5
1
2
1.5
4.5
-0.5
-1
-1.5
新知探究
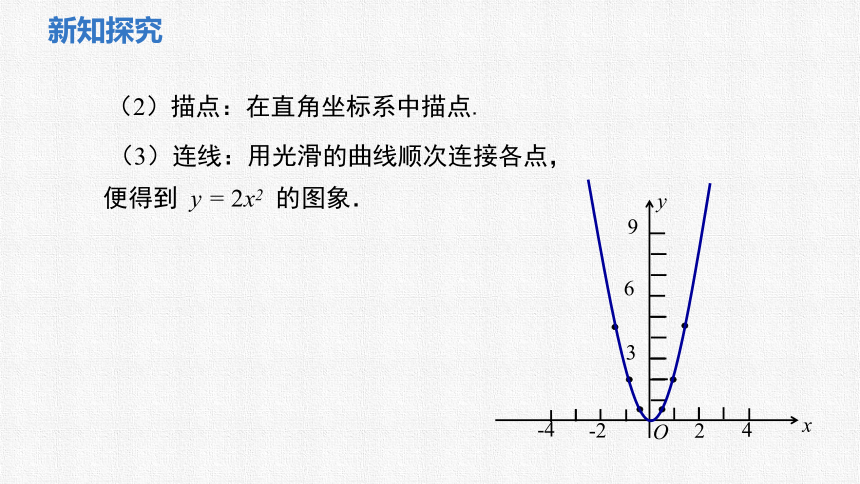
(2)描点:在直角坐标系中描点.
(3)连线:用光滑的曲线顺次连接各点,便得到 y = 2x2 的图象.
2
4
-2
-4
O
3
6
9
x
y
新知探究
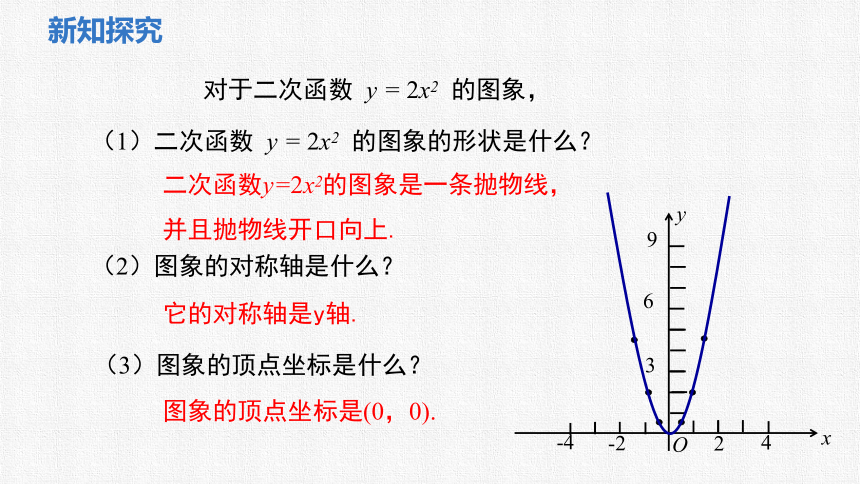
对于二次函数 y = 2x2 的图象,
(1)二次函数 y = 2x2 的图象的形状是什么?
二次函数y=2x2的图象是一条抛物线,
并且抛物线开口向上.
(3)图象的顶点坐标是什么?
图象的顶点坐标是(0,0).
2
4
-2
-4
O
3
6
9
x
y
(2)图象的对称轴是什么?
它的对称轴是y轴.
新知探究
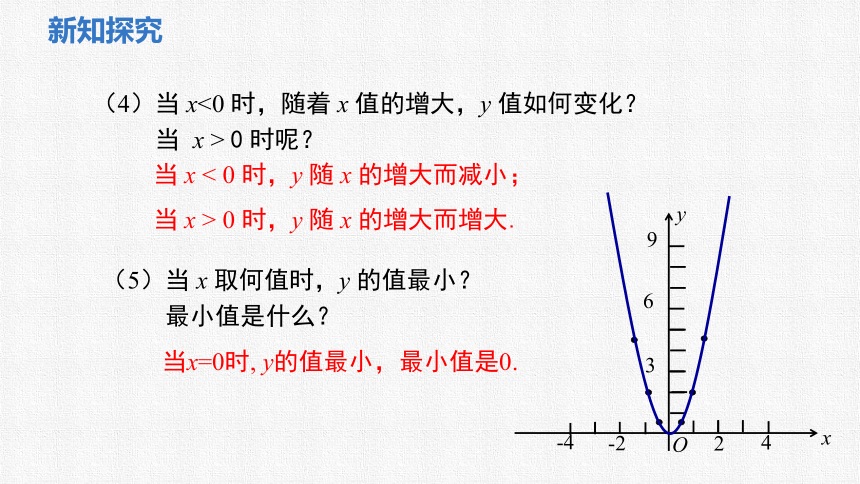
(4)当 x<0 时,随着 x 值的增大,y 值如何变化?
当 x > 0 时呢?
当 x < 0 时,y 随 x 的增大而减小;当 x > 0 时,y 随 x 的增大而增大.
(5)当 x 取何值时,y 的值最小?
最小值是什么?
当x=0时, y的值最小,最小值是0.
2
4
-2
-4
O
3
6
9
x
y
新知探究
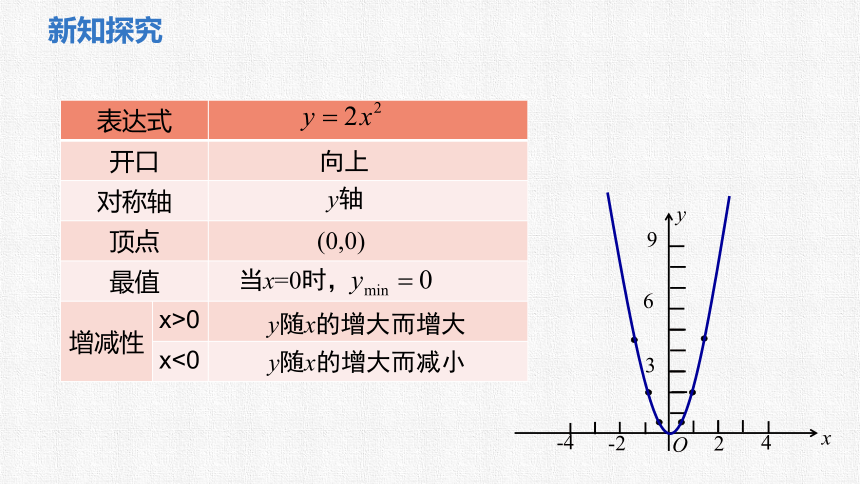
表达式
开口
对称轴
顶点
最值
增减性 x>0
x<0
向上
y轴
(0,0)
当x=0时,
y随x的增大而增大
y随x的增大而减小
2
4
-2
-4
O
3
6
9
x
y
新知探究
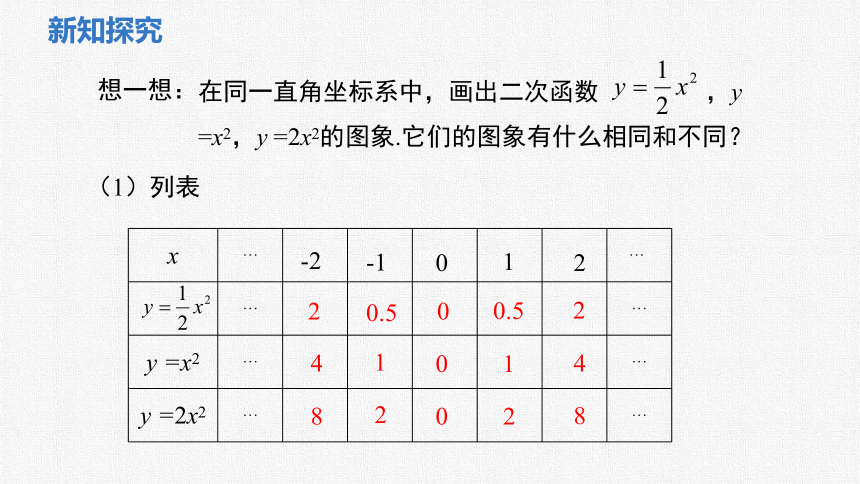
在同一直角坐标系中,画出二次函数 ,y =x2,y =2x2的图象.它们的图象有什么相同和不同?
想一想:
x ··· -2 0000 ······
··· ···
y =x2 ··· ···
y =2x2 ··· ···
2
4
0.5
1
0
0
0.5
1
2
4
(1)列表
-2
-1
0
1
2
8
2
0
2
8
新知探究
(2)描点
(3)连线
y =x2
y=2x2
1.开口都向上,对称轴都是y轴.
2.当x<0时,y随x增大而减小;
当x>0时,y随x增大而增大.
3.顶点都是原点(0,0),顶点是抛物线的最低点.
相同点:
不同点:
开口大小不同, 抛物线的开口最大,
y=2x2抛物线的开口最小.
新知探究
在同一直角坐标系中,画出二次函数 y = x2,y =-x2,y =-2x2的图象如图,观察其开口大小与a的绝对值有什么关系?
抛物线y=ax2 (a≠0)的形状是由|a|来确定的,|a|越大,开口越小.
新知探究
在同一直角坐标系中,画出y=2x2+1 ,y=2x2-1的图象.
(1)列表
知识点 二次函数y=ax2+c的图象与性质
2
x ··· -2 -1.5 -1 0 1 1.5 2 ···
y = 2x2+1 ··· ···
y = 2x2-1 ··· ···
9
5.5
3
1
3
5.5
9
7
3.5
1
-1
1
3.5
7
(2)描点
(3)连线
新知探究
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
y = 2x2+1
y = 2x2-1
1.二次函数 , 的图象与二次函数 的图象有什么关系?
二次函数y = 2x2向上平移一个单位长度,就得二次函数 y = 2x2+1;向下平移一个单位长度,就得二次函数 y = 2x2-1.
新知探究
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
y = 2x2+1
y = 2x2-1
表达式 开口 对称轴 顶点 最值 增减性 x>0 x<0
向上
y轴
(0,0)
y随x的增
大而增大
y随x的增
大而减小
当x=0时,
向上
y轴
(0,1)
当x=0时,
y随x的增
大而增大
y随x的增
大而减小
向上
y轴
(0,-1)
当x=0时,
y随x的增
大而增大
y随x的增
大而减小
2.它们的开口方向、对称轴、顶点坐标、最值、增减性分别是什么呢?
新知探究
归纳总结:
二次函数 与 的图象的关系:
二次函数 的图象可以由 的图象平移得到:
当c > 0时,向上平移c个单位长度得到.
当c < 0时,向下平移 -c个单位长度得到.
上下平移规律:
平方项不变,常数项上加下减.
新知探究
归纳总结:
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=ax2 +c(a>0)
y=ax2 +c(a<0)
(0,c)
(0,c)
y轴(直线x=0)
y轴(直线x=0)
当c>0时,在x轴的上方(经过一,二象限);当c<0时,与x轴相交(经过一二三四象限).
当c<0时,在x轴的下方(经过三,四象限);当c>0时,与x轴相交(经过一二三四象限).
向上
向下
当x=0时,y的最小值为c.
当x=0时,y的最大值为c.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
课堂小结
二次函数y=ax2+c的图象及性质
图象及性质
与 y=ax2的联系
对于抛物线 y = ax 2+c (a>0),开口向上,对称轴为 y轴,顶点坐标为(0,c),
当x>0时,y随x取值的增大而增大;
当x<0时,y随x取值的增大而减小.
对于抛物线 y = ax 2 +c(a<0),开口向下,对称轴为 y轴,顶点坐标为(0,c),
当x>0时,y随x取值的增大而减小;
当x<0时,y随x取值的增大而增大.
二次函数y=ax2+c的图象可以由 y=ax2 的图象沿y轴上、下平移得到.c为正向上平移;c为负向下平移.
课堂训练
1.(2023 安徽)下列函数中,y的值随x值的增大而减小的是( )
A.y=x2+1 B.y=-x2+1
C.y=2x+1 D.y=-2x+1
D
2. (2023 金山区二模)抛物线y= x2+1在y轴的右侧呈 趋势(填“上升”或者“下降”).
下降
课堂训练
3. (2023 凤城模拟)在同一平面直角坐标系xOy中,一次函数y=ax与二次函数y=ax2+a的图象可能是( )
A. B.
C. D.
C
课堂训练
4. 在同一坐标系中画出y1=2x2,y2=-2x2和y3= x2的图象,正确的是图中的( )
D
课堂训练
5. (2023 延安一模)如图是四个二次函数的图象,则a、b、c、d的大小关系为( )
A.d<c<a<b B.d<c<b<a
C.c<d<a<b D.c<d<b<a
B
课堂训练
6.(2023秋 西华县月考)正方形OAMN的顶点M恰好在函数y=mx2(m>0)的图象上,若正方形OAMN的边长为,且边OA与x轴的正半轴的夹角为15°,则m的值为( )
A. B. C. D.3
C
课堂训练
7.(2023 长春一模)如图,正方形ABCD、CEFG的顶点D、F都在抛物线y=- x2上,点B、C、E均在y轴上.若点O是BC边的中点,则正方形CEFG的边长为 .
1+
课堂训练
8. (2023 迁安市模拟)已知二次函数y=ax2,当x=3时,y=3.
(1)求当x=-2时,y的值.
(2)写出它的图象的对称轴、顶点坐标和开口方向.
解:(1)把x=3,y=3代入y=ax2,得a×(32)=3.解得a=.
∴这个二次函数的表达式为y=x2.当x=-2时,y=×(-2)2=.
(2)∵y=x2,a=>0,
∴图象开口向上;对称轴是直线x=0,顶点坐标是(0,0).
第二章 二次函数
2 二次函数的图象与性质
北师大版-数学-九年级下册
第2课时 二次函数y =ax2 和 y =ax2+c的图象与性质
学习目标
【重点】会画y=ax2和y=ax2+c(a≠0)的图象,掌握两者之间的联系.
【难点】灵活运用y=ax2和y=ax2+c(a≠0)的图象,体会数与形的相互联系.
1.会画二次函数y=ax2和y=ax2+c(a≠0)的图象.
2.掌握二次函数y=ax2与y=ax2+c(a≠0)图象之间的联系.
3.能灵活运用二次函数y=ax2和y=ax2+c(a≠0)的知识解决问题.
新课导入
回顾二次函数
y=x 和y=-x 的
图象和性质:
图象
开口 方向
对称性 顶点 最值
增减性
开口向上,在x轴上方
开口向下,在x轴下方
关于y轴对称,对称轴方程是直线x=0
顶点坐标是原点(0,0)
当x=0时,y最小值=0
当x=0时,y最大值=0
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
y
O
x
y
O
x
思考:有没有其他形式的二次函数?
新知探究
画二次函数 的图象
(1)列表:观察 的表达式,选择适当的x值, 并计算相应的y值,完成下表:
知识点 二次函数y=ax2的图象与性质
1
x
4.5
2
0.5
0
0
0.5
0.5
1
2
1.5
4.5
-0.5
-1
-1.5
新知探究
(2)描点:在直角坐标系中描点.
(3)连线:用光滑的曲线顺次连接各点,便得到 y = 2x2 的图象.
2
4
-2
-4
O
3
6
9
x
y
新知探究
对于二次函数 y = 2x2 的图象,
(1)二次函数 y = 2x2 的图象的形状是什么?
二次函数y=2x2的图象是一条抛物线,
并且抛物线开口向上.
(3)图象的顶点坐标是什么?
图象的顶点坐标是(0,0).
2
4
-2
-4
O
3
6
9
x
y
(2)图象的对称轴是什么?
它的对称轴是y轴.
新知探究
(4)当 x<0 时,随着 x 值的增大,y 值如何变化?
当 x > 0 时呢?
当 x < 0 时,y 随 x 的增大而减小;当 x > 0 时,y 随 x 的增大而增大.
(5)当 x 取何值时,y 的值最小?
最小值是什么?
当x=0时, y的值最小,最小值是0.
2
4
-2
-4
O
3
6
9
x
y
新知探究
表达式
开口
对称轴
顶点
最值
增减性 x>0
x<0
向上
y轴
(0,0)
当x=0时,
y随x的增大而增大
y随x的增大而减小
2
4
-2
-4
O
3
6
9
x
y
新知探究
在同一直角坐标系中,画出二次函数 ,y =x2,y =2x2的图象.它们的图象有什么相同和不同?
想一想:
x ··· -2 0000 ······
··· ···
y =x2 ··· ···
y =2x2 ··· ···
2
4
0.5
1
0
0
0.5
1
2
4
(1)列表
-2
-1
0
1
2
8
2
0
2
8
新知探究
(2)描点
(3)连线
y =x2
y=2x2
1.开口都向上,对称轴都是y轴.
2.当x<0时,y随x增大而减小;
当x>0时,y随x增大而增大.
3.顶点都是原点(0,0),顶点是抛物线的最低点.
相同点:
不同点:
开口大小不同, 抛物线的开口最大,
y=2x2抛物线的开口最小.
新知探究
在同一直角坐标系中,画出二次函数 y = x2,y =-x2,y =-2x2的图象如图,观察其开口大小与a的绝对值有什么关系?
抛物线y=ax2 (a≠0)的形状是由|a|来确定的,|a|越大,开口越小.
新知探究
在同一直角坐标系中,画出y=2x2+1 ,y=2x2-1的图象.
(1)列表
知识点 二次函数y=ax2+c的图象与性质
2
x ··· -2 -1.5 -1 0 1 1.5 2 ···
y = 2x2+1 ··· ···
y = 2x2-1 ··· ···
9
5.5
3
1
3
5.5
9
7
3.5
1
-1
1
3.5
7
(2)描点
(3)连线
新知探究
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
y = 2x2+1
y = 2x2-1
1.二次函数 , 的图象与二次函数 的图象有什么关系?
二次函数y = 2x2向上平移一个单位长度,就得二次函数 y = 2x2+1;向下平移一个单位长度,就得二次函数 y = 2x2-1.
新知探究
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
y = 2x2+1
y = 2x2-1
表达式 开口 对称轴 顶点 最值 增减性 x>0 x<0
向上
y轴
(0,0)
y随x的增
大而增大
y随x的增
大而减小
当x=0时,
向上
y轴
(0,1)
当x=0时,
y随x的增
大而增大
y随x的增
大而减小
向上
y轴
(0,-1)
当x=0时,
y随x的增
大而增大
y随x的增
大而减小
2.它们的开口方向、对称轴、顶点坐标、最值、增减性分别是什么呢?
新知探究
归纳总结:
二次函数 与 的图象的关系:
二次函数 的图象可以由 的图象平移得到:
当c > 0时,向上平移c个单位长度得到.
当c < 0时,向下平移 -c个单位长度得到.
上下平移规律:
平方项不变,常数项上加下减.
新知探究
归纳总结:
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=ax2 +c(a>0)
y=ax2 +c(a<0)
(0,c)
(0,c)
y轴(直线x=0)
y轴(直线x=0)
当c>0时,在x轴的上方(经过一,二象限);当c<0时,与x轴相交(经过一二三四象限).
当c<0时,在x轴的下方(经过三,四象限);当c>0时,与x轴相交(经过一二三四象限).
向上
向下
当x=0时,y的最小值为c.
当x=0时,y的最大值为c.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
课堂小结
二次函数y=ax2+c的图象及性质
图象及性质
与 y=ax2的联系
对于抛物线 y = ax 2+c (a>0),开口向上,对称轴为 y轴,顶点坐标为(0,c),
当x>0时,y随x取值的增大而增大;
当x<0时,y随x取值的增大而减小.
对于抛物线 y = ax 2 +c(a<0),开口向下,对称轴为 y轴,顶点坐标为(0,c),
当x>0时,y随x取值的增大而减小;
当x<0时,y随x取值的增大而增大.
二次函数y=ax2+c的图象可以由 y=ax2 的图象沿y轴上、下平移得到.c为正向上平移;c为负向下平移.
课堂训练
1.(2023 安徽)下列函数中,y的值随x值的增大而减小的是( )
A.y=x2+1 B.y=-x2+1
C.y=2x+1 D.y=-2x+1
D
2. (2023 金山区二模)抛物线y= x2+1在y轴的右侧呈 趋势(填“上升”或者“下降”).
下降
课堂训练
3. (2023 凤城模拟)在同一平面直角坐标系xOy中,一次函数y=ax与二次函数y=ax2+a的图象可能是( )
A. B.
C. D.
C
课堂训练
4. 在同一坐标系中画出y1=2x2,y2=-2x2和y3= x2的图象,正确的是图中的( )
D
课堂训练
5. (2023 延安一模)如图是四个二次函数的图象,则a、b、c、d的大小关系为( )
A.d<c<a<b B.d<c<b<a
C.c<d<a<b D.c<d<b<a
B
课堂训练
6.(2023秋 西华县月考)正方形OAMN的顶点M恰好在函数y=mx2(m>0)的图象上,若正方形OAMN的边长为,且边OA与x轴的正半轴的夹角为15°,则m的值为( )
A. B. C. D.3
C
课堂训练
7.(2023 长春一模)如图,正方形ABCD、CEFG的顶点D、F都在抛物线y=- x2上,点B、C、E均在y轴上.若点O是BC边的中点,则正方形CEFG的边长为 .
1+
课堂训练
8. (2023 迁安市模拟)已知二次函数y=ax2,当x=3时,y=3.
(1)求当x=-2时,y的值.
(2)写出它的图象的对称轴、顶点坐标和开口方向.
解:(1)把x=3,y=3代入y=ax2,得a×(32)=3.解得a=.
∴这个二次函数的表达式为y=x2.当x=-2时,y=×(-2)2=.
(2)∵y=x2,a=>0,
∴图象开口向上;对称轴是直线x=0,顶点坐标是(0,0).
