2.2.3二次函数y = a(x-h)2和 y =a(x-h)2+k的图象与性质 课件 (共22张PPT)2024-2025学年数学北师大版九年级下册
文档属性
| 名称 | 2.2.3二次函数y = a(x-h)2和 y =a(x-h)2+k的图象与性质 课件 (共22张PPT)2024-2025学年数学北师大版九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 625.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-13 00:00:00 | ||
图片预览




文档简介
(共22张PPT)
第二章 二次函数
2 二次函数的图象与性质
北师大版-数学-九年级下册
第3课时 二次函数y = a(x-h)2 和 y =a(x-h)2+k的图象与性质
学习目标
【重点】会画y=a(x-h)2和y=a(x-h)2+k(a≠0)的图象,理解其性质.
【难点】掌握y=ax2,y=a(x-h)2和y=a(x-h)2+k(a≠0)之间的联系.
1.会画二次函数y=a(x-h)2和y=a(x-h)2+k (a≠0)的图象.
2.理解二次函数y=a(x-h)2和y=a(x-h)2+k (a≠0)的性质.
3.掌握二次函数y=ax2,y=a(x-h)2和y=a(x-h)2+k (a≠0)之间的联系.
新课导入
二次函数y=ax2和y=ax2+c的图象有什么关系?
二次函数y=ax2+c的图象可以由y=ax2的图象平移得到:
当c > 0时,向上平移c个单位长度得到.
当c < 0时,向下平移 |c|个单位长度得到.
二次函数 y = a(x-h)2 的图象是否可以由 y = ax2 平移得到?
新知探究
画二次函数y=2(x-1)2的图象
(1)完成下表:
知识点 二次函数y=a(x-h)2的图象与性质
1
x -4-4
-4
50
-2
-1
0
1
2
3
-3
4
0
2
8
18
32
2
8
18
32
0
2
8
18
2
8
18
32
观察上表,你能发现2(x-1) 与2x 的值有什么关系?
新知探究
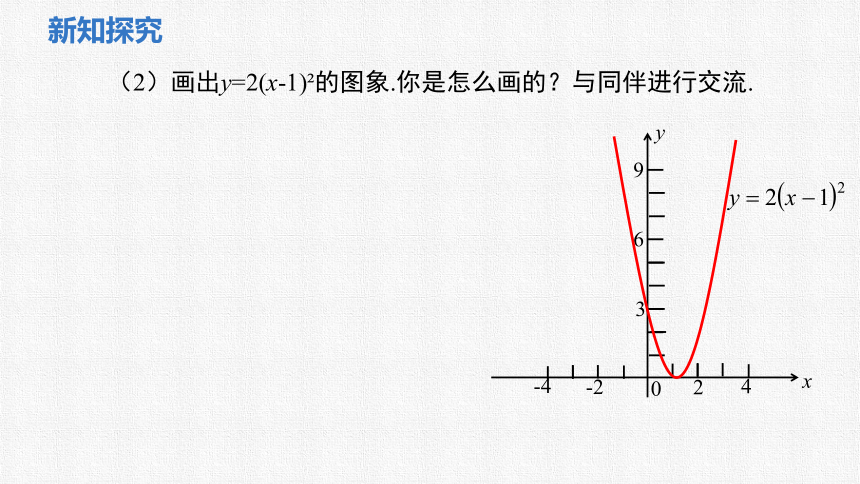
(2)画出y=2(x-1) 的图象.你是怎么画的?与同伴进行交流.
2
4
-2
-4
0
3
6
9
x
y
新知探究
议一议:
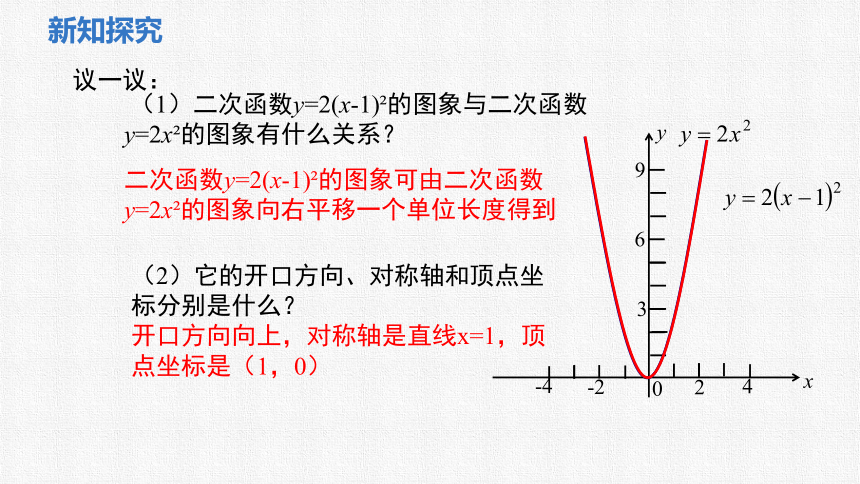
(1)二次函数y=2(x-1) 的图象与二次函数 y=2x 的图象有什么关系?
二次函数y=2(x-1) 的图象可由二次函数 y=2x 的图象向右平移一个单位长度得到
2
4
-2
-4
0
3
6
9
x
y
(2)它的开口方向、对称轴和顶点坐标分别是什么?
开口方向向上,对称轴是直线x=1,顶点坐标是(1,0)
新知探究
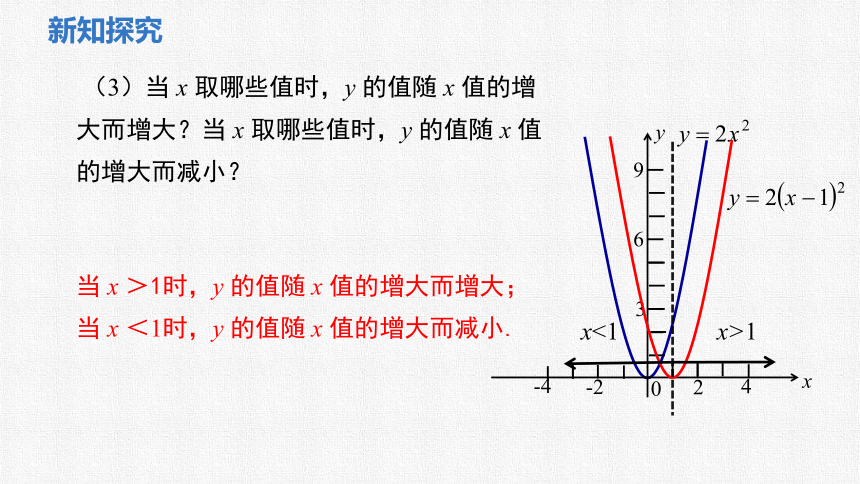
(3)当 x 取哪些值时,y 的值随 x 值的增大而增大?当 x 取哪些值时,y 的值随 x 值的增大而减小?
当 x >1时,y 的值随 x 值的增大而增大;当 x <1时,y 的值随 x 值的增大而减小.
2
4
-2
-4
0
3
6
9
x
y
x>1
x<1
新知探究
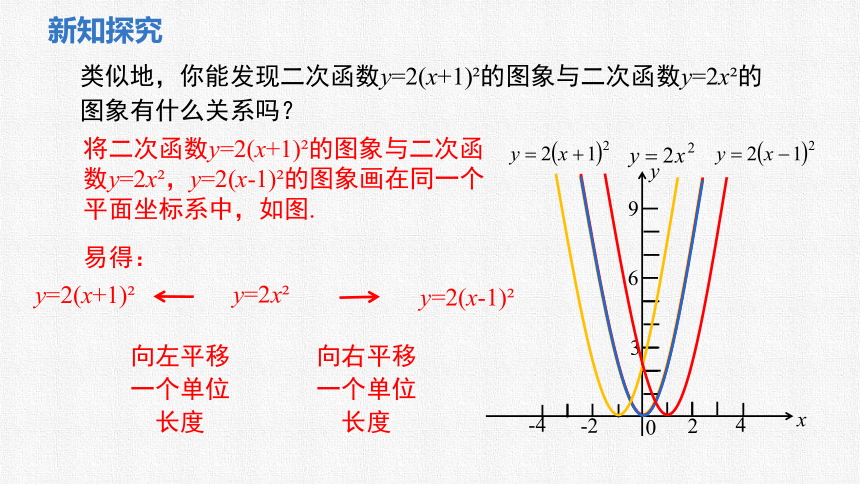
类似地,你能发现二次函数y=2(x+1) 的图象与二次函数y=2x 的图象有什么关系吗?
将二次函数y=2(x+1) 的图象与二次函数y=2x ,y=2(x-1) 的图象画在同一个平面坐标系中,如图.
2
4
-2
-4
0
3
6
9
x
y
y=2x
向左平移一个单位长度
向右平移一个单位长度
y=2(x-1)
y=2(x+1)
易得:
新知探究
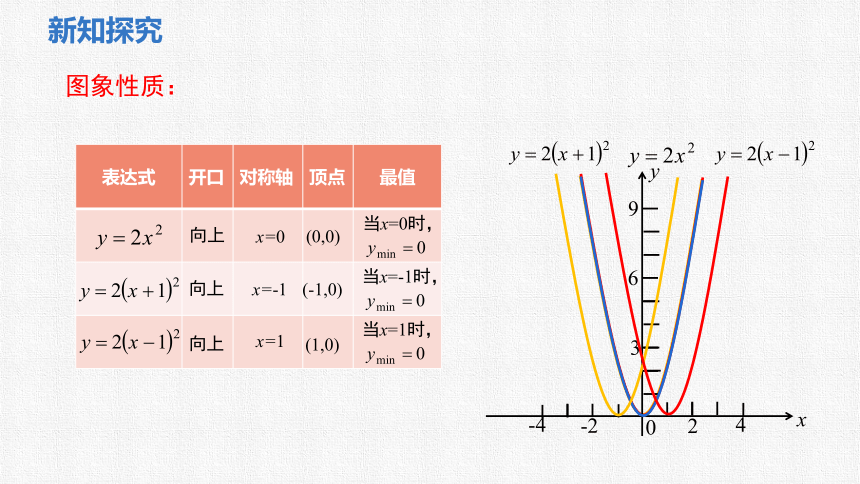
图象性质:
表达式 开口 对称轴 顶点 最值
向上
x=0
(0,0)
当x=0时,
向上
x=-1
(-1,0)
当x=-1时,
向上
x=1
(1,0)
当x=1时,
2
4
-2
-4
0
3
6
9
x
y
新知探究
归纳总结:
y=a(x-h)2
当h>0时,向右平移h个单位长度;
当h<0时,向左平移|h|个单位长度.
二次函数 的图象与 的图象的关系:
y=ax2
左右平移规律:
括号内左加右减;括号外不变.
新知探究
开口 对称轴 顶点 最值 增减性 x>h xa>0
a<0
向上
x=h
(h,0)
y随x的增大而增大
y随x的增大而减小
当x=h时,
向下
x=h
(h,0)
当x=h时,
二次函数y=a(x-h)2的图象与性质:
y随x的增大而减小
y随x的增大而增大
新知探究
随堂练习:
1. 把抛物线 y = -3x2 沿着 x 轴方向平移 2 个单位长度,那么平移后抛物线的表达式是 .
2. 二次函数 y = 2(x - )2 图象的对称轴是直线_______,顶点坐标是 .
y = -3(x+2)2 或y = -3(x-2)2
x=
新知探究
由二次函数y=2x2的图象,你能得到二次函数的图象吗?你是怎样得到的?与同伴进行交流.
知识点 二次函数y=a(x-h)2+k的图象与性质
2
方法一:函数y=2x2先向左平移3个单位长度,再向下平移个单位长度.
方法二:函数y=2x2先向下平移个单位长度,再向左平移3个单位长度.
新知探究
y=a(x-h)2+k 开口 对称轴 顶点 最值 增减性 x>h xa>0
a<0
向上
x=h
(h,k)
y随x的增大而增大
y随x的增大而减小
当x=h时,
向下
x=h
(h,k)
当x=h时,
二次函数y=a(x-h)2+k的图象与性质:
y随x的增大而减小
y随x的增大而增大
新知探究
归纳总结:
一般地,平移二次函数y=ax2的图象便可得到二次函数y=a (x-h)2+k的图象.因此,二次函数y=a (x-h)2+k的图象是一条抛物线,它的开口方向、对称轴和顶点坐标如下表所示:
开口方向 对称轴 顶点坐标
y=a (x-h)2+k 向上a>0 直线x=h (h,k)
向下a<0 课堂小结
当 a>0,开口向上;当 a<0,开口向下.
对称轴是 x = h,
顶点坐标是(h,k).
左右平移:括号内左加右减;
上下平移:括号外上加下减.
一般地,抛物线 y = a(x-h)2+k 与y = ax2 形状相同,位置不同.
二次函数
y = a(x-h)2+k 图象与性质
图象特点
平移规律
课堂训练
1. (2023 海陵区校级二模)已知点A(a,2),B(b,6),C(c,d)都在抛物线y=(x-1)2-2上,d<1.下列选项正确的是( )
A.若a<0,b<0,则b<c<a
B.若a>0,b<0.则b<a<c
C.若a<0,b>0,则a<c<b
D.若a>0,b>0,则c<b<a
C
课堂训练
2.(2023 雁塔区一模)对于二次函数y=-4(x+6)2-5的图象,下列说法正确的是( )
A.图象与y轴交点的坐标是(0,5)
B.对称轴是直线x=6
C.顶点坐标为(-6,5)
D.当x<-6时,y随x的增大而增大
D
课堂训练
3. (2023 立山区一模)二次函数y=a(x-2)2+c与一次函数y=cx+a在同一坐标系中的大致图象是( )
B
A B C D
课堂训练
5.(2023秋 西华县月考)将二次函数y=3(x-1)2+2的图象先向右平移2个单位,再向下平移3个单位,得到的图象对应的表达式是 .
4. (2023 宿豫区三模)抛物线y=(x-4)2+5的顶点坐标是 .
(4,5)
y=3(x-3)2-1
课堂训练
6. (2023秋 朝阳区校级月考)已知二次函数y=-(x+1)2+4.
(1)在平面直角坐标系xOy中画出该函数的图象;
解:抛物线y=-(x+1)2+4的顶点坐标为(-1,4),当x=0时,y=-(x+1)2+4=3,则抛物线与y轴的交点坐标为(0,3);
根据对称轴为直线x=-1,得抛物线必过点(-2,3),
当y=0时,-(x+1)2+4=0.解得x1=1,x2=-3.则抛物线与x轴的交点坐标为(-3,0),(1,0).
过以上五点描点、连线作出抛物线,如图.
课堂训练
(2)当-3≤x≤0时,结合函数图象,直接写出y的取值范围.
解:当-3≤x≤0时,0≤y≤4.
第二章 二次函数
2 二次函数的图象与性质
北师大版-数学-九年级下册
第3课时 二次函数y = a(x-h)2 和 y =a(x-h)2+k的图象与性质
学习目标
【重点】会画y=a(x-h)2和y=a(x-h)2+k(a≠0)的图象,理解其性质.
【难点】掌握y=ax2,y=a(x-h)2和y=a(x-h)2+k(a≠0)之间的联系.
1.会画二次函数y=a(x-h)2和y=a(x-h)2+k (a≠0)的图象.
2.理解二次函数y=a(x-h)2和y=a(x-h)2+k (a≠0)的性质.
3.掌握二次函数y=ax2,y=a(x-h)2和y=a(x-h)2+k (a≠0)之间的联系.
新课导入
二次函数y=ax2和y=ax2+c的图象有什么关系?
二次函数y=ax2+c的图象可以由y=ax2的图象平移得到:
当c > 0时,向上平移c个单位长度得到.
当c < 0时,向下平移 |c|个单位长度得到.
二次函数 y = a(x-h)2 的图象是否可以由 y = ax2 平移得到?
新知探究
画二次函数y=2(x-1)2的图象
(1)完成下表:
知识点 二次函数y=a(x-h)2的图象与性质
1
x -4-4
-4
50
-2
-1
0
1
2
3
-3
4
0
2
8
18
32
2
8
18
32
0
2
8
18
2
8
18
32
观察上表,你能发现2(x-1) 与2x 的值有什么关系?
新知探究
(2)画出y=2(x-1) 的图象.你是怎么画的?与同伴进行交流.
2
4
-2
-4
0
3
6
9
x
y
新知探究
议一议:
(1)二次函数y=2(x-1) 的图象与二次函数 y=2x 的图象有什么关系?
二次函数y=2(x-1) 的图象可由二次函数 y=2x 的图象向右平移一个单位长度得到
2
4
-2
-4
0
3
6
9
x
y
(2)它的开口方向、对称轴和顶点坐标分别是什么?
开口方向向上,对称轴是直线x=1,顶点坐标是(1,0)
新知探究
(3)当 x 取哪些值时,y 的值随 x 值的增大而增大?当 x 取哪些值时,y 的值随 x 值的增大而减小?
当 x >1时,y 的值随 x 值的增大而增大;当 x <1时,y 的值随 x 值的增大而减小.
2
4
-2
-4
0
3
6
9
x
y
x>1
x<1
新知探究
类似地,你能发现二次函数y=2(x+1) 的图象与二次函数y=2x 的图象有什么关系吗?
将二次函数y=2(x+1) 的图象与二次函数y=2x ,y=2(x-1) 的图象画在同一个平面坐标系中,如图.
2
4
-2
-4
0
3
6
9
x
y
y=2x
向左平移一个单位长度
向右平移一个单位长度
y=2(x-1)
y=2(x+1)
易得:
新知探究
图象性质:
表达式 开口 对称轴 顶点 最值
向上
x=0
(0,0)
当x=0时,
向上
x=-1
(-1,0)
当x=-1时,
向上
x=1
(1,0)
当x=1时,
2
4
-2
-4
0
3
6
9
x
y
新知探究
归纳总结:
y=a(x-h)2
当h>0时,向右平移h个单位长度;
当h<0时,向左平移|h|个单位长度.
二次函数 的图象与 的图象的关系:
y=ax2
左右平移规律:
括号内左加右减;括号外不变.
新知探究
开口 对称轴 顶点 最值 增减性 x>h x
a<0
向上
x=h
(h,0)
y随x的增大而增大
y随x的增大而减小
当x=h时,
向下
x=h
(h,0)
当x=h时,
二次函数y=a(x-h)2的图象与性质:
y随x的增大而减小
y随x的增大而增大
新知探究
随堂练习:
1. 把抛物线 y = -3x2 沿着 x 轴方向平移 2 个单位长度,那么平移后抛物线的表达式是 .
2. 二次函数 y = 2(x - )2 图象的对称轴是直线_______,顶点坐标是 .
y = -3(x+2)2 或y = -3(x-2)2
x=
新知探究
由二次函数y=2x2的图象,你能得到二次函数的图象吗?你是怎样得到的?与同伴进行交流.
知识点 二次函数y=a(x-h)2+k的图象与性质
2
方法一:函数y=2x2先向左平移3个单位长度,再向下平移个单位长度.
方法二:函数y=2x2先向下平移个单位长度,再向左平移3个单位长度.
新知探究
y=a(x-h)2+k 开口 对称轴 顶点 最值 增减性 x>h x
a<0
向上
x=h
(h,k)
y随x的增大而增大
y随x的增大而减小
当x=h时,
向下
x=h
(h,k)
当x=h时,
二次函数y=a(x-h)2+k的图象与性质:
y随x的增大而减小
y随x的增大而增大
新知探究
归纳总结:
一般地,平移二次函数y=ax2的图象便可得到二次函数y=a (x-h)2+k的图象.因此,二次函数y=a (x-h)2+k的图象是一条抛物线,它的开口方向、对称轴和顶点坐标如下表所示:
开口方向 对称轴 顶点坐标
y=a (x-h)2+k 向上a>0 直线x=h (h,k)
向下a<0 课堂小结
当 a>0,开口向上;当 a<0,开口向下.
对称轴是 x = h,
顶点坐标是(h,k).
左右平移:括号内左加右减;
上下平移:括号外上加下减.
一般地,抛物线 y = a(x-h)2+k 与y = ax2 形状相同,位置不同.
二次函数
y = a(x-h)2+k 图象与性质
图象特点
平移规律
课堂训练
1. (2023 海陵区校级二模)已知点A(a,2),B(b,6),C(c,d)都在抛物线y=(x-1)2-2上,d<1.下列选项正确的是( )
A.若a<0,b<0,则b<c<a
B.若a>0,b<0.则b<a<c
C.若a<0,b>0,则a<c<b
D.若a>0,b>0,则c<b<a
C
课堂训练
2.(2023 雁塔区一模)对于二次函数y=-4(x+6)2-5的图象,下列说法正确的是( )
A.图象与y轴交点的坐标是(0,5)
B.对称轴是直线x=6
C.顶点坐标为(-6,5)
D.当x<-6时,y随x的增大而增大
D
课堂训练
3. (2023 立山区一模)二次函数y=a(x-2)2+c与一次函数y=cx+a在同一坐标系中的大致图象是( )
B
A B C D
课堂训练
5.(2023秋 西华县月考)将二次函数y=3(x-1)2+2的图象先向右平移2个单位,再向下平移3个单位,得到的图象对应的表达式是 .
4. (2023 宿豫区三模)抛物线y=(x-4)2+5的顶点坐标是 .
(4,5)
y=3(x-3)2-1
课堂训练
6. (2023秋 朝阳区校级月考)已知二次函数y=-(x+1)2+4.
(1)在平面直角坐标系xOy中画出该函数的图象;
解:抛物线y=-(x+1)2+4的顶点坐标为(-1,4),当x=0时,y=-(x+1)2+4=3,则抛物线与y轴的交点坐标为(0,3);
根据对称轴为直线x=-1,得抛物线必过点(-2,3),
当y=0时,-(x+1)2+4=0.解得x1=1,x2=-3.则抛物线与x轴的交点坐标为(-3,0),(1,0).
过以上五点描点、连线作出抛物线,如图.
课堂训练
(2)当-3≤x≤0时,结合函数图象,直接写出y的取值范围.
解:当-3≤x≤0时,0≤y≤4.
