2.4.1面积最值与抛物线型问题 课件 (共27张PPT)2024-2025学年数学北师大版九年级下册
文档属性
| 名称 | 2.4.1面积最值与抛物线型问题 课件 (共27张PPT)2024-2025学年数学北师大版九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-13 21:17:59 | ||
图片预览





文档简介
(共27张PPT)
第二章 二次函数
4 二次函数的应用
北师大版-数学-九年级下册
第1课时 面积最值与抛物线型问题
学习目标
1.分析实际问题中变量之间的二次函数关系.
2.能应用二次函数的性质解决图形中最大面积问题.
3.会运用二次函数解决抛物线型问题.
【重点】能根据实际问题列出函数关系式,并根据问题的实际情况确定自变量取何值时,函数取得最值.
【难点】通过建立二次函数的数学模型解决实际问题,在解决问题的过程中体会数形结合思想.
新课导入
想一想:如何求出二次函数 y = ax2 + bx + c 的最小(大)值?
抛物线y = ax 2 + bx + c 的顶点是最低(高)点,当x=时,二次函数 y = ax 2 + bx + c 有最小(大) 值y=.
新知探究
知识点 求二次函数的最大值与最小值
1
问题1 根据自变量的取值范围求出二次函数 y = ax2 + bx + c 的最小(大)值.
(1)当自变量的取值范围是全体实数时,
解:若a>0,则在顶点处取得最小值,此时不存在最大值;
若a<0,则在顶点处取得最大值,此时不存在最小值.
新知探究
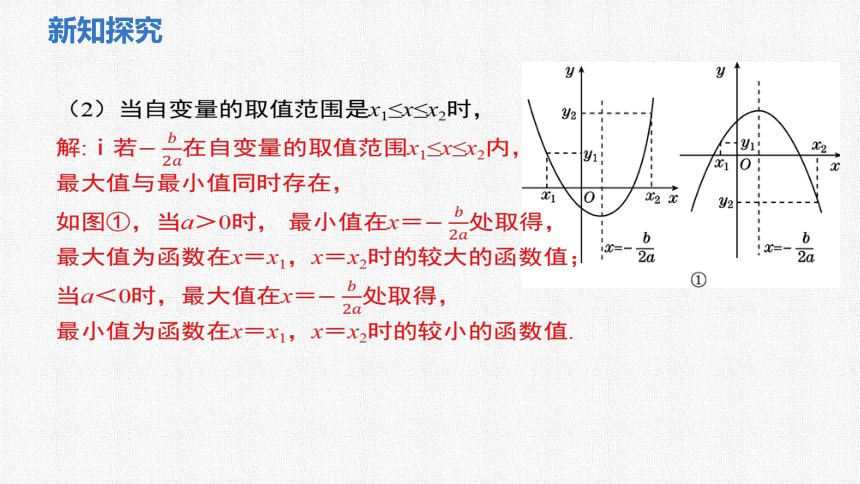
(2)当自变量的取值范围是x1≤x≤x2时,
解:ⅰ若在自变量的取值范围x1≤x≤x2内,
最大值与最小值同时存在,
如图①,当a>0时, 最小值在x=处取得,
最大值为函数在x=x1,x=x2时的较大的函数值;
当a<0时,最大值在x=处取得,
最小值为函数在x=x1,x=x2时的较小的函数值.
新知探究
ⅱ若不在自变量的取值范围x1≤x≤x2内,最大值和最小值同时存在,且在x=x1,x=x2时的函数值中,较大的为最大值,较小的为最小值,如图②.
新知探究
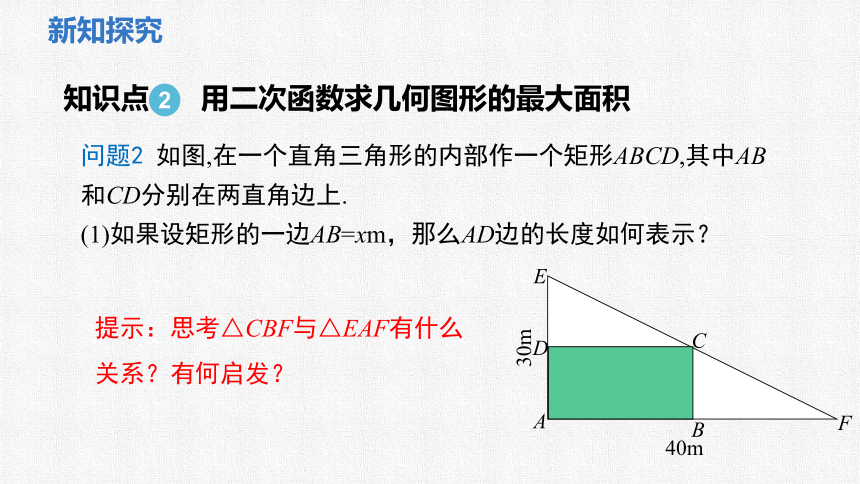
问题2 如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和CD分别在两直角边上.
(1)如果设矩形的一边AB=xm,那么AD边的长度如何表示?
知识点 用二次函数求几何图形的最大面积
2
提示:思考△CBF与△EAF有什么关系?有何启发?
F
E
A
C
D
40m
30m
B
新知探究
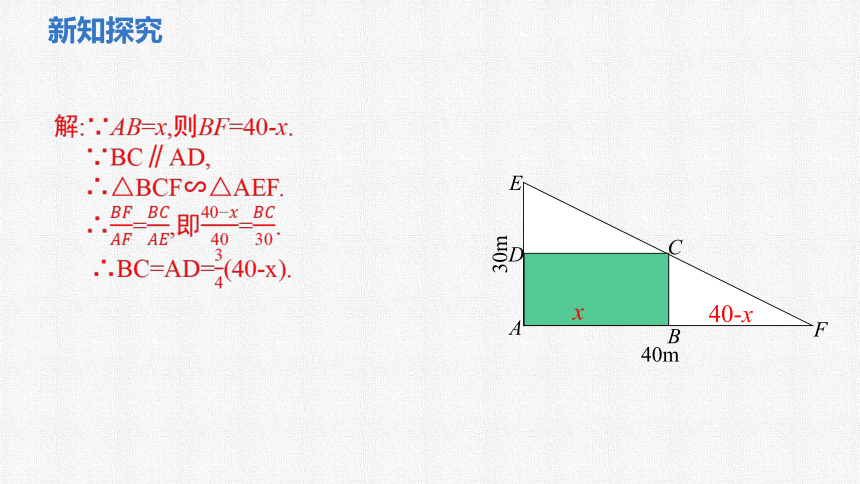
解:∵AB=x,则BF=40-x.
∵BC∥AD,
∴△BCF∽△AEF.
∴=,即=.
∴BC=AD=(40-x).
F
E
A
C
D
40m
30m
B
x
40-x
新知探究
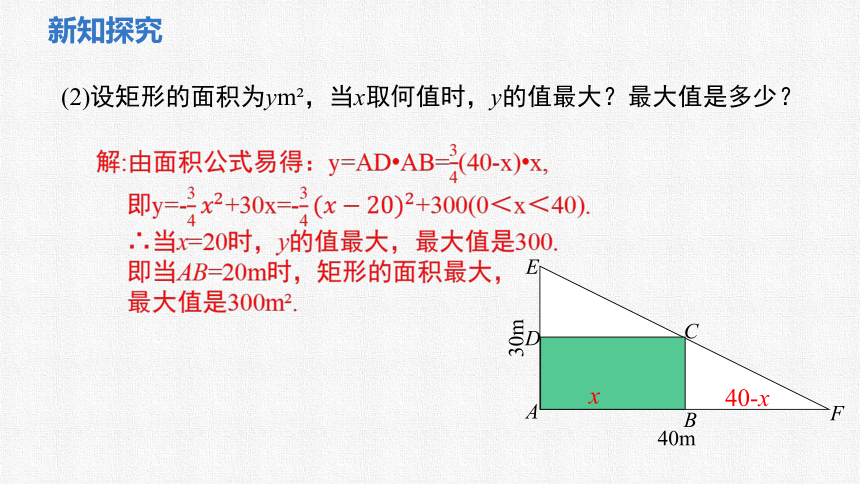
(2)设矩形的面积为ym ,当x取何值时,y的值最大?最大值是多少?
F
E
A
C
D
40m
30m
B
x
40-x
解:由面积公式易得:y=AD AB=(40-x) x,
即y=-+30x=-+300(0<x<40).
∴当x=20时,y的值最大,最大值是300.
即当AB=20m时,矩形的面积最大,
最大值是300m .
新知探究
在上面的问题中,如果把矩形改为如图所示的位置,其他条件不变,那么矩形的最大面积是多少?你是怎样知道的?
议一议:
提示:类比原题的方法,思考能否利用相似表示AD?
A
C
D
40m
30m
B
O
F
E
新知探究
解:过点O作OM⊥EF于点M,交AD于点N,由勾股定理易得EF=50m,由等面积法可得OM=24m.
设AB=x,则MN=AB=x,ON=OM-MN=24-x.
由△AOD∽△FOE,得= ,
即=∴AD=50-x.
易得y=AD AB=(50-x) x=-(x-12)2+300.
∴当AB=12m时,矩形的面积最大,
最大值是300m .
A
C
D
40m
30m
B
O
F
E
∟
∟
M
N
新知探究
例1 某建筑物的窗户如图所示,它的上半部分是半圆,下半部分是矩形,制造窗框的材料总长(图中所有黑线的长度和)为15m.当x等于多少时,窗户通过的光线最多?(结果精确到0.01m)此时,窗户的面积是多少?(结果精确到0.01m2)
解:∵7x+4y+πx=15,
∴0<x<1.48.
x
x
y
注意:利用二次函数解决实际问题,必须求出自变量取值范围.
新知探究
设窗户的面积是S m2, 则
因此,当x约为1.07m时,窗户通过的光线最多.此时,窗户的面积约为4.02 m2.
新知探究
二次函数解决几何面积最值问题的方法:
归纳总结:
①求出函数表达式和自变量的取值范围;
②配方变形,或利用公式求它的最大值或最小值;
③检查求得的最大值或最小值对应的自变量的值,使之必须在自变量的取值范围内.
新知探究
知识点 利用二次函数解决抛物线型问题
3
问题3 如图,隧道的截面由抛物线和长方形构成.长方形的长是8米,
宽是2米,抛物线可以用y=-x2+4表示.
(1)一辆货运卡车高4米,宽2米,它能通过该隧道吗?
(2)如果该隧道内设双向车道,那么这辆货运
卡车是否可以通过?
2
4
-2
-4
o
3
x
y
新知探究
(2)由(1),得当y=2时,x=,
∵>2,∴这两货运卡车能通过.
2
4
-2
-4
o
3
x
y
解:(1)把y=4-2=2代入y=-x2+4,得2=-x2+4.
解得x=,则此时可通过货运卡车的宽度为米.
∴高4米,宽2米的卡车能通过该隧道.
新知探究
问题4 如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m.水面下降1m,水面宽度增加多少?
提示:将实际问题转化为数学问题,先建立适当的坐标系求出这条抛物线表示的二次函数,再根据二次函数的图象进行解题.
新知探究
1
-2
-1
2
3
y
O
-1
-2
1
2
x
解: 建立如图所示的平面直角坐标系,
设这条抛物线表示的二次函数为y=ax2.
由抛物线经过点(2,-2),可得-2=a×22.
解得a= .
∴这条抛物线表示的二次函数为y= x2.
当水面下降1m时,水面的纵坐标为y=-3,
这时有-3= x2,解得x=± .
∴这时水面宽度为 m.
答:当水面下降1m时,水面宽度增加 m.
新知探究
抛物线型问题的一般解题步骤:
归纳总结:
①建立适当的平面直角系,并将已知条件转化为点的坐标;
②合理地设出所求的函数的表达式,并代入已知条件或点的坐标,求出关系式;
③利用关系式求解实际问题.
课堂小结
几何面积最值问题
关键
注意
(二次函数的图象和性质)
转化
回归
(实物中的抛物线型问题)
实际问题
数学模型
常见几何图形的面积公式
依 据
建立函数关系式
最值有时不在顶点处,则要利用函数的增减性来确定
课堂小结
抛物线型问题
建立恰当的直角坐标系
能够将实际距离准确的转化为点的坐标;
选择运算简便的方法.
转化关键
课堂训练
1.(2023秋 瑞安市月考)已知某种产品的成本价为30元/千克,经市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=-2x+80.设这种产品每天的销售利润为w(元),则w与x之间的函数表达式为( )
A.w=(x-30)(-2x+80) B.w=x(-2x+80)
C.w=30(-2x+80) D.w=x(-2x+50)
A
课堂训练
2.(2023 老河口市模拟)在综合实践活动中,同学们借助如图所示的直角墙角(两边足够长),用24m长的篱笆围成一个矩形花园ABCD,则矩形花园ABCD的最大面积为 m2.
3.(2023秋 沙市区期中)汽车刹车后行驶的距离s(单位:m)关于行驶的时间t(单位:s)的函数表达式是s=15t-6t2,汽车刹车后到停下来,所需的时间为 .(单位:s)
144
1.25
课堂训练
4. (2023 原平市一模)在2023年中考体育考试前,小康对自己某次实心球的训练录像进行了分析,发现实心球飞行路线是一条抛物线,若不考虑空气阻力,实心球的飞行高度y(单位:米)与飞行的水平距离x(单位:米)之间具有函数关系y=-x2+x+,则小康这次实心球训练的成绩为( )
A.14米 B.12米 C.11米 D.10米
B
课堂训练
5.(2023秋 西青区期中)如图所示是抛物线型的拱桥,当拱顶离水面2米时,水面宽4米,如果水面宽为2米,则水面下降( )米.
A.1米 B.2米 C.3米 D.10米
A
课堂训练
6. (2023秋 古冶区期中)某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米,若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由.
课堂训练
解:设这个苗圃园垂直于墙的一边的长为x米,则平行于墙的一边长为30-2x米.
根据题意,得S=x(30-2x)=-2x2+30x=-2(x-)2+,
8≤30-2x≤18.
解得6≤x≤11.
∴当x>时,S随x的增大而减小,
∴当x=7.5时,S最大值=;当x=11时,S最小值=11×(30-22)=88.
第二章 二次函数
4 二次函数的应用
北师大版-数学-九年级下册
第1课时 面积最值与抛物线型问题
学习目标
1.分析实际问题中变量之间的二次函数关系.
2.能应用二次函数的性质解决图形中最大面积问题.
3.会运用二次函数解决抛物线型问题.
【重点】能根据实际问题列出函数关系式,并根据问题的实际情况确定自变量取何值时,函数取得最值.
【难点】通过建立二次函数的数学模型解决实际问题,在解决问题的过程中体会数形结合思想.
新课导入
想一想:如何求出二次函数 y = ax2 + bx + c 的最小(大)值?
抛物线y = ax 2 + bx + c 的顶点是最低(高)点,当x=时,二次函数 y = ax 2 + bx + c 有最小(大) 值y=.
新知探究
知识点 求二次函数的最大值与最小值
1
问题1 根据自变量的取值范围求出二次函数 y = ax2 + bx + c 的最小(大)值.
(1)当自变量的取值范围是全体实数时,
解:若a>0,则在顶点处取得最小值,此时不存在最大值;
若a<0,则在顶点处取得最大值,此时不存在最小值.
新知探究
(2)当自变量的取值范围是x1≤x≤x2时,
解:ⅰ若在自变量的取值范围x1≤x≤x2内,
最大值与最小值同时存在,
如图①,当a>0时, 最小值在x=处取得,
最大值为函数在x=x1,x=x2时的较大的函数值;
当a<0时,最大值在x=处取得,
最小值为函数在x=x1,x=x2时的较小的函数值.
新知探究
ⅱ若不在自变量的取值范围x1≤x≤x2内,最大值和最小值同时存在,且在x=x1,x=x2时的函数值中,较大的为最大值,较小的为最小值,如图②.
新知探究
问题2 如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和CD分别在两直角边上.
(1)如果设矩形的一边AB=xm,那么AD边的长度如何表示?
知识点 用二次函数求几何图形的最大面积
2
提示:思考△CBF与△EAF有什么关系?有何启发?
F
E
A
C
D
40m
30m
B
新知探究
解:∵AB=x,则BF=40-x.
∵BC∥AD,
∴△BCF∽△AEF.
∴=,即=.
∴BC=AD=(40-x).
F
E
A
C
D
40m
30m
B
x
40-x
新知探究
(2)设矩形的面积为ym ,当x取何值时,y的值最大?最大值是多少?
F
E
A
C
D
40m
30m
B
x
40-x
解:由面积公式易得:y=AD AB=(40-x) x,
即y=-+30x=-+300(0<x<40).
∴当x=20时,y的值最大,最大值是300.
即当AB=20m时,矩形的面积最大,
最大值是300m .
新知探究
在上面的问题中,如果把矩形改为如图所示的位置,其他条件不变,那么矩形的最大面积是多少?你是怎样知道的?
议一议:
提示:类比原题的方法,思考能否利用相似表示AD?
A
C
D
40m
30m
B
O
F
E
新知探究
解:过点O作OM⊥EF于点M,交AD于点N,由勾股定理易得EF=50m,由等面积法可得OM=24m.
设AB=x,则MN=AB=x,ON=OM-MN=24-x.
由△AOD∽△FOE,得= ,
即=∴AD=50-x.
易得y=AD AB=(50-x) x=-(x-12)2+300.
∴当AB=12m时,矩形的面积最大,
最大值是300m .
A
C
D
40m
30m
B
O
F
E
∟
∟
M
N
新知探究
例1 某建筑物的窗户如图所示,它的上半部分是半圆,下半部分是矩形,制造窗框的材料总长(图中所有黑线的长度和)为15m.当x等于多少时,窗户通过的光线最多?(结果精确到0.01m)此时,窗户的面积是多少?(结果精确到0.01m2)
解:∵7x+4y+πx=15,
∴0<x<1.48.
x
x
y
注意:利用二次函数解决实际问题,必须求出自变量取值范围.
新知探究
设窗户的面积是S m2, 则
因此,当x约为1.07m时,窗户通过的光线最多.此时,窗户的面积约为4.02 m2.
新知探究
二次函数解决几何面积最值问题的方法:
归纳总结:
①求出函数表达式和自变量的取值范围;
②配方变形,或利用公式求它的最大值或最小值;
③检查求得的最大值或最小值对应的自变量的值,使之必须在自变量的取值范围内.
新知探究
知识点 利用二次函数解决抛物线型问题
3
问题3 如图,隧道的截面由抛物线和长方形构成.长方形的长是8米,
宽是2米,抛物线可以用y=-x2+4表示.
(1)一辆货运卡车高4米,宽2米,它能通过该隧道吗?
(2)如果该隧道内设双向车道,那么这辆货运
卡车是否可以通过?
2
4
-2
-4
o
3
x
y
新知探究
(2)由(1),得当y=2时,x=,
∵>2,∴这两货运卡车能通过.
2
4
-2
-4
o
3
x
y
解:(1)把y=4-2=2代入y=-x2+4,得2=-x2+4.
解得x=,则此时可通过货运卡车的宽度为米.
∴高4米,宽2米的卡车能通过该隧道.
新知探究
问题4 如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m.水面下降1m,水面宽度增加多少?
提示:将实际问题转化为数学问题,先建立适当的坐标系求出这条抛物线表示的二次函数,再根据二次函数的图象进行解题.
新知探究
1
-2
-1
2
3
y
O
-1
-2
1
2
x
解: 建立如图所示的平面直角坐标系,
设这条抛物线表示的二次函数为y=ax2.
由抛物线经过点(2,-2),可得-2=a×22.
解得a= .
∴这条抛物线表示的二次函数为y= x2.
当水面下降1m时,水面的纵坐标为y=-3,
这时有-3= x2,解得x=± .
∴这时水面宽度为 m.
答:当水面下降1m时,水面宽度增加 m.
新知探究
抛物线型问题的一般解题步骤:
归纳总结:
①建立适当的平面直角系,并将已知条件转化为点的坐标;
②合理地设出所求的函数的表达式,并代入已知条件或点的坐标,求出关系式;
③利用关系式求解实际问题.
课堂小结
几何面积最值问题
关键
注意
(二次函数的图象和性质)
转化
回归
(实物中的抛物线型问题)
实际问题
数学模型
常见几何图形的面积公式
依 据
建立函数关系式
最值有时不在顶点处,则要利用函数的增减性来确定
课堂小结
抛物线型问题
建立恰当的直角坐标系
能够将实际距离准确的转化为点的坐标;
选择运算简便的方法.
转化关键
课堂训练
1.(2023秋 瑞安市月考)已知某种产品的成本价为30元/千克,经市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=-2x+80.设这种产品每天的销售利润为w(元),则w与x之间的函数表达式为( )
A.w=(x-30)(-2x+80) B.w=x(-2x+80)
C.w=30(-2x+80) D.w=x(-2x+50)
A
课堂训练
2.(2023 老河口市模拟)在综合实践活动中,同学们借助如图所示的直角墙角(两边足够长),用24m长的篱笆围成一个矩形花园ABCD,则矩形花园ABCD的最大面积为 m2.
3.(2023秋 沙市区期中)汽车刹车后行驶的距离s(单位:m)关于行驶的时间t(单位:s)的函数表达式是s=15t-6t2,汽车刹车后到停下来,所需的时间为 .(单位:s)
144
1.25
课堂训练
4. (2023 原平市一模)在2023年中考体育考试前,小康对自己某次实心球的训练录像进行了分析,发现实心球飞行路线是一条抛物线,若不考虑空气阻力,实心球的飞行高度y(单位:米)与飞行的水平距离x(单位:米)之间具有函数关系y=-x2+x+,则小康这次实心球训练的成绩为( )
A.14米 B.12米 C.11米 D.10米
B
课堂训练
5.(2023秋 西青区期中)如图所示是抛物线型的拱桥,当拱顶离水面2米时,水面宽4米,如果水面宽为2米,则水面下降( )米.
A.1米 B.2米 C.3米 D.10米
A
课堂训练
6. (2023秋 古冶区期中)某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米,若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由.
课堂训练
解:设这个苗圃园垂直于墙的一边的长为x米,则平行于墙的一边长为30-2x米.
根据题意,得S=x(30-2x)=-2x2+30x=-2(x-)2+,
8≤30-2x≤18.
解得6≤x≤11.
∴当x>时,S随x的增大而减小,
∴当x=7.5时,S最大值=;当x=11时,S最小值=11×(30-22)=88.
