2.5.1二次函数与一元二次方程的关系 课件 (共22张PPT) 2024-2025学年数学北师大版九年级下册
文档属性
| 名称 | 2.5.1二次函数与一元二次方程的关系 课件 (共22张PPT) 2024-2025学年数学北师大版九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-13 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
第二章 二次函数
5 二次函数与一元二次方程
北师大版-数学-九年级下册
第1课时 二次函数与一元二次方程的关系
学习目标
1.理解二次函数与一元二次方程之间的联系.
2.理解二次函数与x 轴交点的个数与一元二次方程的根的关系.
3.能运用二次函数及其图象、性质确定方程的解.
【重点】经历探索二次函数与一元二次方程的关系的过程,体会方程与函数之间的联系.
【难点】通过观察二次函数与x 轴交点的个数,讨论一元二次方程的根的情况.
新课导入
1、一元二次方程ax2+bx+c=0(a≠0)的根的判别式△ =______.
当△﹥0时,方程根的情况是____________________;
当△=0时,方程根的情况是____________________;
当△﹤0时,方程根的情况是______________.
b2-4ac
有两个不等实数根
有两个相等实数根
没有实数根
2、二次函数y=ax2+bx+c(a、b、c是常数,且a≠0)图象是一条___________,它与x轴的交点有几种可能的情况?
抛物线
三种可能:①两个交点 ②一个交点 ③没有交点.
新知探究
知识点 二次函数与一元二次方程的关系
1
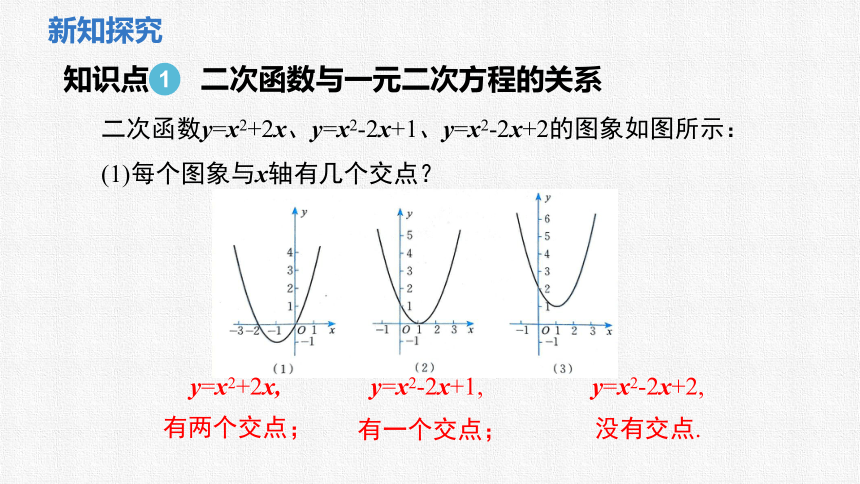
二次函数y=x2+2x、y=x2-2x+1、y=x2-2x+2的图象如图所示:
(1)每个图象与x轴有几个交点?
有两个交点;
有一个交点;
没有交点.
y=x2+2x,
y=x2-2x+1,
y=x2-2x+2,
新知探究
(2) 一元二次方程 x2+2x=0, x2-2x+1=0有几个实数根
一元二次方程 x2-2x+2=0 有实数根吗 请分别求出它们的根.
(3)二次函数y=ax2+bx+c的图象与x轴的交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系?
新知探究
1.二次函数y=x2+2x的图象
①图象与x轴有____个交点;
②交点坐标为__________.
一元二次方程x2+2x=0根的情况
①方程有__个_______的实数根;
②方程的根是_____________.
2
(-2,0),(0,0)
2
不相等
x1=-2, x2=0
解:x(x+2)=0
x1=-2,x2=0.
新知探究
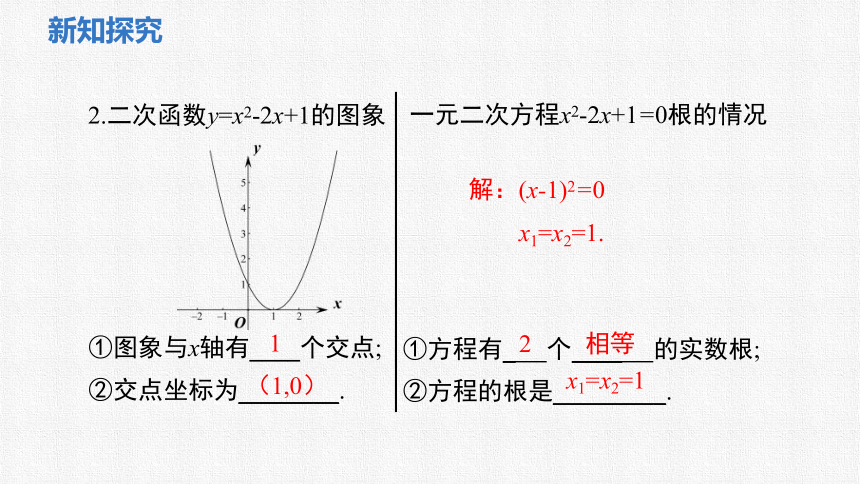
2.二次函数y=x2-2x+1的图象
①图象与x轴有____个交点;
②交点坐标为________.
一元二次方程x2-2x+1=0根的情况
①方程有_ 个____ 的实数根;
②方程的根是_________.
1
(1,0)
2
相等
x1=x2=1
解:(x-1)2=0
x1=x2=1.
新知探究
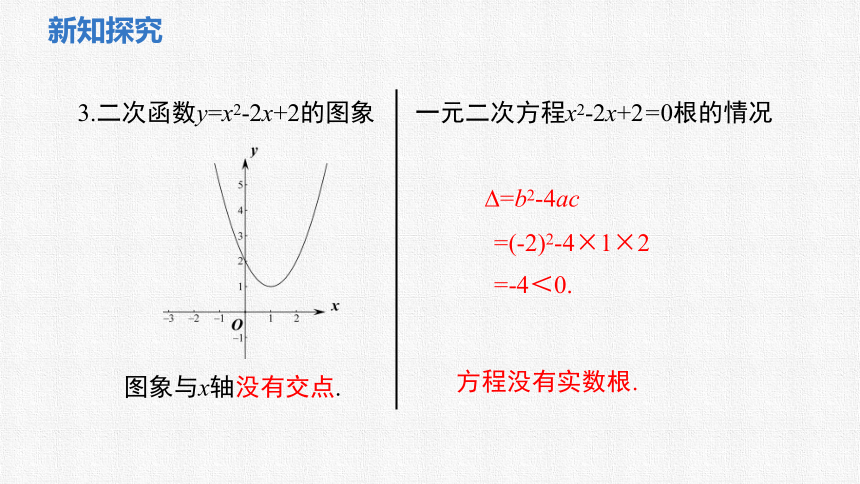
3.二次函数y=x2-2x+2的图象
图象与x轴没有交点.
一元二次方程x2-2x+2=0根的情况
方程没有实数根.
=b2-4ac
=(-2)2-4×1×2
=-4<0.
新知探究
二次函数图象与x轴的交点坐标
y=x2+2x
y=x2-2x+1
y=x2-2x+2
x2+2x=0
x2-2x+1=0
x2-2x+2=0
一元二次方程的根
(-2,0),(0,0)
(1,0)
没有交点;
x1=-2, x2=0
x1=x2=1
方程没有实数根.
2个交点;
1个交点;
方程2个不相等实数根;
方程2个相等实数根;
新知探究
二次函数y=ax2+bx+c的图象与x轴的交点的坐标和一元二次方程ax2+bx+c=0的根的关系:
归纳总结:
二次函数y=ax2+bx +c的图象与x轴交点 一元二次方程 ax2+bx+c=0的根 △=b2-4ac
有两个交点
有两个不相等的实数根,为交点的横坐标
△ > 0
有一个交点
有两个相等的实数根,为交点的横坐标
△ = 0
没有交点
没有实数根
△ < 0
新知探究
以 40 m /s的速度将小球沿与地面成 30°角的方向击出时,球的飞行路线是一条抛物线,如果不考虑空气阻力,球的飞行高度 h (单位:m)与飞行时间 t (单位:s)之间具有关系:h= 20t–5t2 .
你能否解决以下问题:
知识点 运动中的抛物线问题
2
新知探究
解:解方程20t-5t2=15,
t2-4t+3=0,
t1=1,t2=3.
∴当球飞行1s和3s时,它的高度为15m.
(1)球的飞行高度能否达到 15 m 若能,需要多少时间
y/m
O
t/s
15
1
3
新知探究
解:解方程20t-5t2=20,
t2-4t+4=0,
t1=t2=2.
∴当球飞行2s时,它的高度为20m.
(2)小球的飞行高度能否达到 20 m 若能,需要多少时间
y/m
O
t/s
20
2
新知探究
解:解方程20t-5t2=20.5,
t2-4t+4.1=0.
∵(-4)2-4×4.1<0,
∴球的飞行高度达不到20.5m.
(3)小球的飞行高度能否达到20.5m?
如果能,需要多少飞行时间?
y/m
O
t/s
20.5
新知探究
解:解方程20t-5t2=0,
t2-4t=0,
t1=0,t2=4.
∴当球飞行0s和4s时,它的高度为0m,
即小球从飞出到落地要用4秒.
(4)小球从飞出到落地要用多少时间?
y/m
O
t/s
4
新知探究
归纳总结:
已知二次函数y的值为m,求相应自变量x的值,
就是求相应一元二次方程的解.
例如,已知二次函数y = -x2+4x的值为3,求自变量x的值,可以解一元二次方程-x2+4x=3(即x2-4x+3=0).
反过来,解方程x2-4x+3=0 又可以看作已知二次函数 y = x2-4x+3 的值为0,求自变量x的值.
课堂小结
二次函数与一元二次方程
二次函数与一元二次方程的关系
y=ax2+bx+c(a≠0),当y取定值时就成了一元二次方程;ax2+bx+c=0(a≠0),右边换成y时就成了二次函数.
二次函数与一元二次方程根的情况
二次函数与x轴的交点个数
判别式 的符号
一元二次方程根的情况
课堂训练
1.已知抛物线y=ax2+bx+c与x轴有两个不同的交点,则关于x的一元二次方程ax2+bx+c=0根的情况是 ( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.无实数根
D.无法确定
A
课堂训练
2.二次函数y=ax2+bx+c的图象如图所示,则方程ax2+bx+c=0 的根是( )
A.x1=1,x2=-1
B.x1=0,x2=2
C.x1=-1,x2=2
D.x1=1,x2=0
C
课堂训练
3.二次函数y=ax2+bx+c(a≠0)中,____________决定其图象与x轴交点的个数,当b2-4ac____0时,抛物线与x轴有两个交点;当b2-4ac____0时,抛物线与x轴有一个交点,当b2-4ac____0时,抛物线与x轴没有交点.
4.抛物线y=x2-6x+5,与x轴有____个交点,分别是_______ ___.
5.抛物线y=x2-x+5,与x轴_____交点,且图象都位于x轴的_______.
b2-4ac
=
<
两
(1,0)、(5,0)
没有
上方
>
课堂训练
6. 如图,某学生推铅球,铅球出手(点A处)的高度是0.6m,出手后的铅球沿一段抛物线运行,当运行到最高3m时,水平距离x=4m.
(1)求这个二次函数的表达式;
解:(1)设二次函数的表达式为y=a(x-4)2+3.
把(0,0.6)代入,得 0.6=a(0-4)2+3.解得a=-.
∴y=-(x-4)2+3,即这个二次函数的表达式为y=-(x-4)2+3.
课堂训练
(2)该同学把铅球推出去多远?
解:当y=0时,0=-(x-4)2+3.
解得(舍去).
答:该男同学把铅球推出去()m远.
第二章 二次函数
5 二次函数与一元二次方程
北师大版-数学-九年级下册
第1课时 二次函数与一元二次方程的关系
学习目标
1.理解二次函数与一元二次方程之间的联系.
2.理解二次函数与x 轴交点的个数与一元二次方程的根的关系.
3.能运用二次函数及其图象、性质确定方程的解.
【重点】经历探索二次函数与一元二次方程的关系的过程,体会方程与函数之间的联系.
【难点】通过观察二次函数与x 轴交点的个数,讨论一元二次方程的根的情况.
新课导入
1、一元二次方程ax2+bx+c=0(a≠0)的根的判别式△ =______.
当△﹥0时,方程根的情况是____________________;
当△=0时,方程根的情况是____________________;
当△﹤0时,方程根的情况是______________.
b2-4ac
有两个不等实数根
有两个相等实数根
没有实数根
2、二次函数y=ax2+bx+c(a、b、c是常数,且a≠0)图象是一条___________,它与x轴的交点有几种可能的情况?
抛物线
三种可能:①两个交点 ②一个交点 ③没有交点.
新知探究
知识点 二次函数与一元二次方程的关系
1
二次函数y=x2+2x、y=x2-2x+1、y=x2-2x+2的图象如图所示:
(1)每个图象与x轴有几个交点?
有两个交点;
有一个交点;
没有交点.
y=x2+2x,
y=x2-2x+1,
y=x2-2x+2,
新知探究
(2) 一元二次方程 x2+2x=0, x2-2x+1=0有几个实数根
一元二次方程 x2-2x+2=0 有实数根吗 请分别求出它们的根.
(3)二次函数y=ax2+bx+c的图象与x轴的交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系?
新知探究
1.二次函数y=x2+2x的图象
①图象与x轴有____个交点;
②交点坐标为__________.
一元二次方程x2+2x=0根的情况
①方程有__个_______的实数根;
②方程的根是_____________.
2
(-2,0),(0,0)
2
不相等
x1=-2, x2=0
解:x(x+2)=0
x1=-2,x2=0.
新知探究
2.二次函数y=x2-2x+1的图象
①图象与x轴有____个交点;
②交点坐标为________.
一元二次方程x2-2x+1=0根的情况
①方程有_ 个____ 的实数根;
②方程的根是_________.
1
(1,0)
2
相等
x1=x2=1
解:(x-1)2=0
x1=x2=1.
新知探究
3.二次函数y=x2-2x+2的图象
图象与x轴没有交点.
一元二次方程x2-2x+2=0根的情况
方程没有实数根.
=b2-4ac
=(-2)2-4×1×2
=-4<0.
新知探究
二次函数图象与x轴的交点坐标
y=x2+2x
y=x2-2x+1
y=x2-2x+2
x2+2x=0
x2-2x+1=0
x2-2x+2=0
一元二次方程的根
(-2,0),(0,0)
(1,0)
没有交点;
x1=-2, x2=0
x1=x2=1
方程没有实数根.
2个交点;
1个交点;
方程2个不相等实数根;
方程2个相等实数根;
新知探究
二次函数y=ax2+bx+c的图象与x轴的交点的坐标和一元二次方程ax2+bx+c=0的根的关系:
归纳总结:
二次函数y=ax2+bx +c的图象与x轴交点 一元二次方程 ax2+bx+c=0的根 △=b2-4ac
有两个交点
有两个不相等的实数根,为交点的横坐标
△ > 0
有一个交点
有两个相等的实数根,为交点的横坐标
△ = 0
没有交点
没有实数根
△ < 0
新知探究
以 40 m /s的速度将小球沿与地面成 30°角的方向击出时,球的飞行路线是一条抛物线,如果不考虑空气阻力,球的飞行高度 h (单位:m)与飞行时间 t (单位:s)之间具有关系:h= 20t–5t2 .
你能否解决以下问题:
知识点 运动中的抛物线问题
2
新知探究
解:解方程20t-5t2=15,
t2-4t+3=0,
t1=1,t2=3.
∴当球飞行1s和3s时,它的高度为15m.
(1)球的飞行高度能否达到 15 m 若能,需要多少时间
y/m
O
t/s
15
1
3
新知探究
解:解方程20t-5t2=20,
t2-4t+4=0,
t1=t2=2.
∴当球飞行2s时,它的高度为20m.
(2)小球的飞行高度能否达到 20 m 若能,需要多少时间
y/m
O
t/s
20
2
新知探究
解:解方程20t-5t2=20.5,
t2-4t+4.1=0.
∵(-4)2-4×4.1<0,
∴球的飞行高度达不到20.5m.
(3)小球的飞行高度能否达到20.5m?
如果能,需要多少飞行时间?
y/m
O
t/s
20.5
新知探究
解:解方程20t-5t2=0,
t2-4t=0,
t1=0,t2=4.
∴当球飞行0s和4s时,它的高度为0m,
即小球从飞出到落地要用4秒.
(4)小球从飞出到落地要用多少时间?
y/m
O
t/s
4
新知探究
归纳总结:
已知二次函数y的值为m,求相应自变量x的值,
就是求相应一元二次方程的解.
例如,已知二次函数y = -x2+4x的值为3,求自变量x的值,可以解一元二次方程-x2+4x=3(即x2-4x+3=0).
反过来,解方程x2-4x+3=0 又可以看作已知二次函数 y = x2-4x+3 的值为0,求自变量x的值.
课堂小结
二次函数与一元二次方程
二次函数与一元二次方程的关系
y=ax2+bx+c(a≠0),当y取定值时就成了一元二次方程;ax2+bx+c=0(a≠0),右边换成y时就成了二次函数.
二次函数与一元二次方程根的情况
二次函数与x轴的交点个数
判别式 的符号
一元二次方程根的情况
课堂训练
1.已知抛物线y=ax2+bx+c与x轴有两个不同的交点,则关于x的一元二次方程ax2+bx+c=0根的情况是 ( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.无实数根
D.无法确定
A
课堂训练
2.二次函数y=ax2+bx+c的图象如图所示,则方程ax2+bx+c=0 的根是( )
A.x1=1,x2=-1
B.x1=0,x2=2
C.x1=-1,x2=2
D.x1=1,x2=0
C
课堂训练
3.二次函数y=ax2+bx+c(a≠0)中,____________决定其图象与x轴交点的个数,当b2-4ac____0时,抛物线与x轴有两个交点;当b2-4ac____0时,抛物线与x轴有一个交点,当b2-4ac____0时,抛物线与x轴没有交点.
4.抛物线y=x2-6x+5,与x轴有____个交点,分别是_______ ___.
5.抛物线y=x2-x+5,与x轴_____交点,且图象都位于x轴的_______.
b2-4ac
=
<
两
(1,0)、(5,0)
没有
上方
>
课堂训练
6. 如图,某学生推铅球,铅球出手(点A处)的高度是0.6m,出手后的铅球沿一段抛物线运行,当运行到最高3m时,水平距离x=4m.
(1)求这个二次函数的表达式;
解:(1)设二次函数的表达式为y=a(x-4)2+3.
把(0,0.6)代入,得 0.6=a(0-4)2+3.解得a=-.
∴y=-(x-4)2+3,即这个二次函数的表达式为y=-(x-4)2+3.
课堂训练
(2)该同学把铅球推出去多远?
解:当y=0时,0=-(x-4)2+3.
解得(舍去).
答:该男同学把铅球推出去()m远.
