2.5.2利用函数图象求一元二次方程的近似根 课件(共21张PPT) 2024-2025学年数学北师大版九年级下册
文档属性
| 名称 | 2.5.2利用函数图象求一元二次方程的近似根 课件(共21张PPT) 2024-2025学年数学北师大版九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 459.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-13 00:00:00 | ||
图片预览





文档简介
(共21张PPT)
第二章 二次函数
5 二次函数与一元二次方程
北师大版-数学-九年级下册
第2课时 利用函数图象求一元二次方程的近似根
学习目标
1.利用二次函数的图象求一元二次方程的近似根及一元二次不等式的解集.
2.通过研究二次函数与一元二次方程的联系体会数形结合思想的应用.
【重点】会利用二次函数的图象求一元二次方程的近似根.【难点】通过研究二次函数与一元二次方程的联系体会数形结合思想的应用.
新课导入
上节课我们知道二次函数 y=ax2+bx+c(a≠0) 与x轴交点的横坐标是一元二次方程 ax2+bx+c=0(a≠0) 的解,那么如何利用二次函数图象直接求出一元二次方程的根呢
x
y
O
x1
x2
y=ax2+bx+c
新知探究
知识点 利用二次函数的图象求一元二次方程的近似根
1
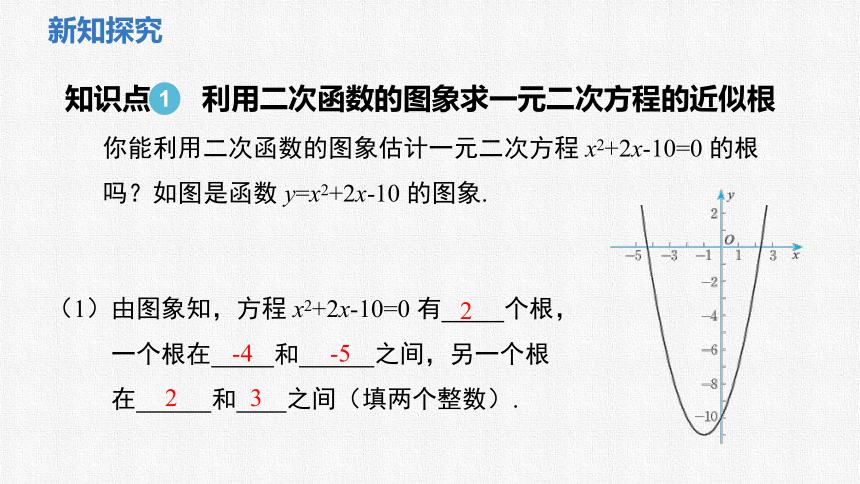
你能利用二次函数的图象估计一元二次方程 x2+2x-10=0 的根吗?如图是函数 y=x2+2x-10 的图象.
(1)由图象知,方程 x2+2x-10=0 有 个根,
一个根在 和 之间,另一个根
在 和 之间(填两个整数).
2
-4
-5
2
3
新知探究
因此 x=-4.3 是方程的一个近似根.
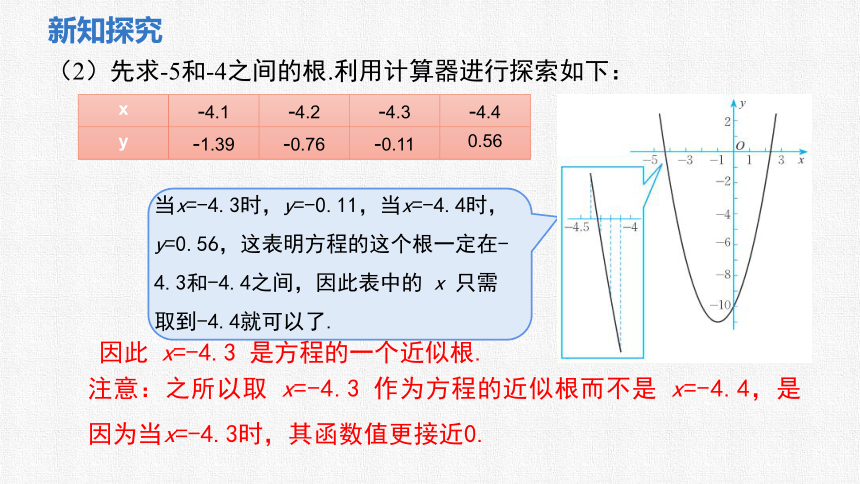
(2)先求-5和-4之间的根.利用计算器进行探索如下:
x -4.1 -4.2 -4.3 -4.4
y -1.39 -0.76 -0.11 0.56
当x=-4.3时,y=-0.11,当x=-4.4时,y=0.56,这表明方程的这个根一定在-4.3和-4.4之间,因此表中的 x 只需取到-4.4就可以了.
注意:之所以取 x=-4.3 作为方程的近似根而不是 x=-4.4,是因为当x=-4.3时,其函数值更接近0.
新知探究
(3)另一个根可以类似地求出:
x 2.1 2.2 2.3 2.4
y -1.39 -0.76 -0.11 0.56
因此 x=2.3是方程的另一个近似根.
新知探究
利用二次函数的图象求一元二次方程的近似根的一般步骤:
归纳总结:
(1)用描点法画出二次函数y=ax2+bx+c的图象;
(2)确定二次函数的图象与x轴交点的个数,看交点的横坐标在哪两个整数之间;
(3)确定方程 ax2+bx+c=0 的近似根.(可将单位长度十等分,借助计算器确定其近似值,两个函数值异号)
新知探究
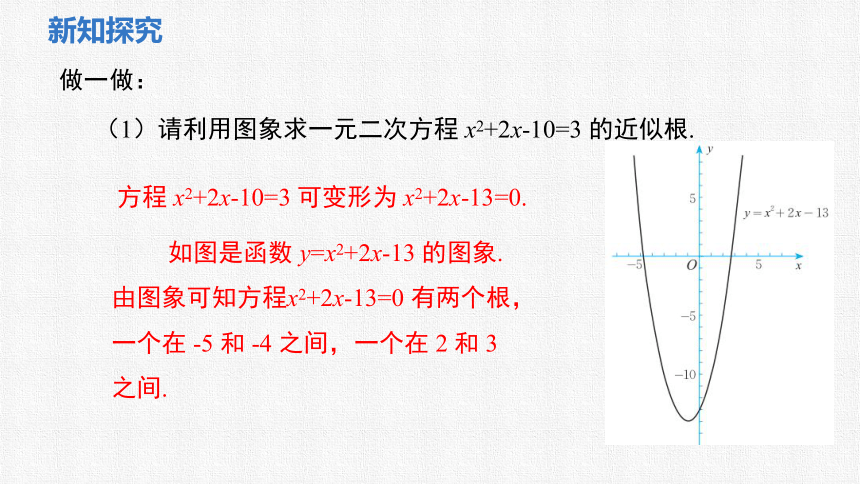
(1)请利用图象求一元二次方程 x2+2x-10=3 的近似根.
做一做:
方程 x2+2x-10=3 可变形为 x2+2x-13=0.
如图是函数 y=x2+2x-13 的图象.由图象可知方程x2+2x-13=0 有两个根,一个在 -5 和 -4 之间,一个在 2 和 3 之间.
新知探究
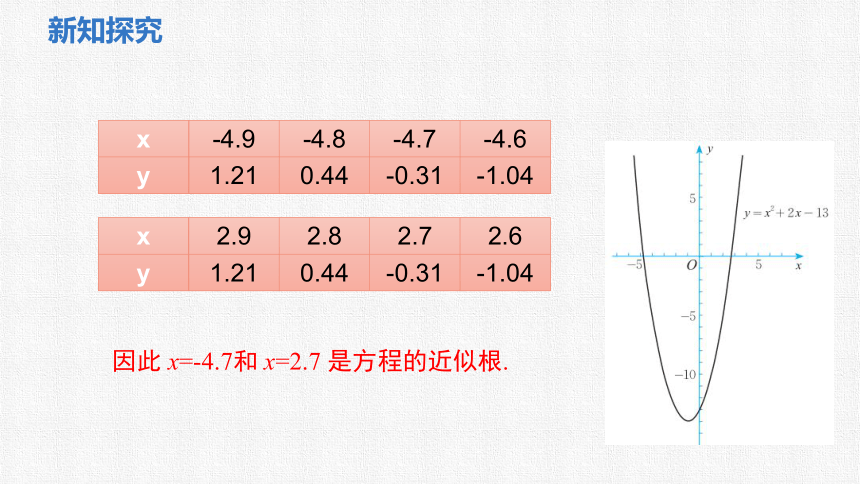
x 2.9 2.8 2.7 2.6
y 1.21 0.44 -0.31 -1.04
x -4.9 -4.8 -4.7 -4.6
y 1.21 0.44 -0.31 -1.04
因此 x=-4.7和 x=2.7 是方程的近似根.
新知探究
(2)请利用如图求一元二次方程 x2+2x-10=3 的近似根.
如图是函数 y=x2+2x-10 的图象.由图象可知方程x2+2x-10=0 有两个根,一个在 -5 和-4 之间,一个在 2 和 3 之间.
新知探究
x 2.9 2.8 2.7 2.6
y 4.21 3.44 2.69 1.96
x -4.9 -4.8 -4.7 -4.6
y 4.21 3.44 2.69 1.96
因此 x=-4.7和 x=2.7 是方程的近似根.
新知探究
问题1 函数 y = ax2+bx+c 的图象如图,那么
方程 ax2+bx+c=0 的根是 ___________;
不等式 ax2+bx+c>0 的解集是_____________;
不等式 ax2+bx+c<0 的解集是___________.
知识点 利用二次函数的图象解一元二次不等式
2
3
-1
x
x1=-1, x2=3
x<-1或x>3
-1新知探究
3
-1
O
x
2
(4,2)
(-2,2)
y
拓展:
函数y=ax2+bx+c的图象如图,那么
方程ax2+bx+c=2的根是 ______________;
不等式ax2+bx+c>2的解集是___________;
不等式ax2+bx+c<2的解集是_________.
x1=-2, x2=4
x<-2或x>4
-2新知探究
问题2 如果不等式 ax2+bx+c>0(a≠0)的解集是 x ≠ 1的一切实数,那么函数 y=ax2+bx+c 的图象与 x 轴有____ 个交点,坐标是______.方程 ax2+bx+c=0 的根是______.
1
(1,0)
x = 1
问题3 如果方程ax2+bx+c=0 (a≠0)没有实数根,那么函数y=ax2+bx+c的图象与 x轴有______个交点;
不等式ax2+bx+c<0的解集是多少?
0
解:当a>0时, ax2+bx+c<0无解;当a<0时, ax2+bx+c<0的解集是一切实数.
新知探究
归纳总结:
二次函数y=ax2+bx+c的图象与x轴交点的坐标与一元二次不等式的关系
二次函数y=ax2+bx+c的图象与x轴交点 a>0 a<0
有两个交点x1,x2 (x1<x2)
有一个交点x0
没有交点
y<0,x1<x<x2.
y>0,x2<x或x<x1
y>0,x1<x<x2.
y<0,x2<x或x<x1
y>0,x0之外的所有实数;y<0,无解
y<0,x0之外的所有实数;y>0,无解
y>0,所有实数;y<0,无解
y<0,所有实数;y>0,无解
课堂小结
二次函数图象
由图象与x轴的交点位置,
判断方程根的近似值
一元二次方程的根
一元二次不等式的解集
课堂训练
1.(2023秋 咸宁期中)方程2x2+x-2=0的近似根可以看作是下列哪两个函数图象交点的横坐标( )
A.y=2x2和y=x-2 B.y=2x2+x和y=2
C.y=2x2-2和y=x D.y=-2x2和y=x+2
B
课堂训练
2.(2023秋 怀远县期中)下表列出了函数y=ax2+bx+c(a≠0)中自变量x与函数y的部分对应值.根据表中数据,判断一元二次方程ax2+bx+c=0(a≠0)的一个解在哪两个相邻的整数之间( )
A.1与2之间 B.-2与-1之间 C.-1与0之间 D.0与1之间
D
课堂训练
3.(2023 东平县校级模拟)如图,二次函数y=ax2+bx+c的部分图象与y轴的交点为(0,3),它的对称轴为直线x=1,则下列结论中:
①c=3;②2a+b=0;③8a-b+c>0;
④方程ax2+bx+c=0的其中一个根在2,3之间.
正确的有 (填序号).
①②④
课堂训练
4.(2023 泰安一模)已知二次函数y=ax2+bx+2的图象(a、b是常数)与y轴交于点A,点A与点B关于抛物线的对称轴对称,且点C(x1,y1),D(x2,y2)在该函数图象上.二次函数y=ax2+bx+2中(b、c是常数)的自变量x与函数值y的部分对应值如表:
下列结论:①点B的坐标是(2,2);②这个函数的最大值大于5;③ax2+bx=-1有一个根在4与5之间;④当0<x1<1,4<x2<5时,y1>y2.其中正确的为 .(将所有正确结论的序号都填入)
②③④
课堂训练
5. (2023秋 怀远县期中)二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象回答下列问题.
(1)写出方程ax2+bx+c=0的根;
(2)写出不等式ax2+bx+c<0的解集;
(3)若方程ax2+bx+c=k无实数根,写出k的取值范围.
解:(1)观察图象可知,方程ax2+bx+c=0的根,即为抛物线与x轴交点的横坐标.∴x1=0,x2=2.
(2)观察图象可知:不等式ax2+bx+c<0的解集为x<0或x>2.
(3)由图象可知,k>2时,方程ax2+bx+c=k无实数根.
第二章 二次函数
5 二次函数与一元二次方程
北师大版-数学-九年级下册
第2课时 利用函数图象求一元二次方程的近似根
学习目标
1.利用二次函数的图象求一元二次方程的近似根及一元二次不等式的解集.
2.通过研究二次函数与一元二次方程的联系体会数形结合思想的应用.
【重点】会利用二次函数的图象求一元二次方程的近似根.【难点】通过研究二次函数与一元二次方程的联系体会数形结合思想的应用.
新课导入
上节课我们知道二次函数 y=ax2+bx+c(a≠0) 与x轴交点的横坐标是一元二次方程 ax2+bx+c=0(a≠0) 的解,那么如何利用二次函数图象直接求出一元二次方程的根呢
x
y
O
x1
x2
y=ax2+bx+c
新知探究
知识点 利用二次函数的图象求一元二次方程的近似根
1
你能利用二次函数的图象估计一元二次方程 x2+2x-10=0 的根吗?如图是函数 y=x2+2x-10 的图象.
(1)由图象知,方程 x2+2x-10=0 有 个根,
一个根在 和 之间,另一个根
在 和 之间(填两个整数).
2
-4
-5
2
3
新知探究
因此 x=-4.3 是方程的一个近似根.
(2)先求-5和-4之间的根.利用计算器进行探索如下:
x -4.1 -4.2 -4.3 -4.4
y -1.39 -0.76 -0.11 0.56
当x=-4.3时,y=-0.11,当x=-4.4时,y=0.56,这表明方程的这个根一定在-4.3和-4.4之间,因此表中的 x 只需取到-4.4就可以了.
注意:之所以取 x=-4.3 作为方程的近似根而不是 x=-4.4,是因为当x=-4.3时,其函数值更接近0.
新知探究
(3)另一个根可以类似地求出:
x 2.1 2.2 2.3 2.4
y -1.39 -0.76 -0.11 0.56
因此 x=2.3是方程的另一个近似根.
新知探究
利用二次函数的图象求一元二次方程的近似根的一般步骤:
归纳总结:
(1)用描点法画出二次函数y=ax2+bx+c的图象;
(2)确定二次函数的图象与x轴交点的个数,看交点的横坐标在哪两个整数之间;
(3)确定方程 ax2+bx+c=0 的近似根.(可将单位长度十等分,借助计算器确定其近似值,两个函数值异号)
新知探究
(1)请利用图象求一元二次方程 x2+2x-10=3 的近似根.
做一做:
方程 x2+2x-10=3 可变形为 x2+2x-13=0.
如图是函数 y=x2+2x-13 的图象.由图象可知方程x2+2x-13=0 有两个根,一个在 -5 和 -4 之间,一个在 2 和 3 之间.
新知探究
x 2.9 2.8 2.7 2.6
y 1.21 0.44 -0.31 -1.04
x -4.9 -4.8 -4.7 -4.6
y 1.21 0.44 -0.31 -1.04
因此 x=-4.7和 x=2.7 是方程的近似根.
新知探究
(2)请利用如图求一元二次方程 x2+2x-10=3 的近似根.
如图是函数 y=x2+2x-10 的图象.由图象可知方程x2+2x-10=0 有两个根,一个在 -5 和-4 之间,一个在 2 和 3 之间.
新知探究
x 2.9 2.8 2.7 2.6
y 4.21 3.44 2.69 1.96
x -4.9 -4.8 -4.7 -4.6
y 4.21 3.44 2.69 1.96
因此 x=-4.7和 x=2.7 是方程的近似根.
新知探究
问题1 函数 y = ax2+bx+c 的图象如图,那么
方程 ax2+bx+c=0 的根是 ___________;
不等式 ax2+bx+c>0 的解集是_____________;
不等式 ax2+bx+c<0 的解集是___________.
知识点 利用二次函数的图象解一元二次不等式
2
3
-1
x
x1=-1, x2=3
x<-1或x>3
-1
3
-1
O
x
2
(4,2)
(-2,2)
y
拓展:
函数y=ax2+bx+c的图象如图,那么
方程ax2+bx+c=2的根是 ______________;
不等式ax2+bx+c>2的解集是___________;
不等式ax2+bx+c<2的解集是_________.
x1=-2, x2=4
x<-2或x>4
-2
问题2 如果不等式 ax2+bx+c>0(a≠0)的解集是 x ≠ 1的一切实数,那么函数 y=ax2+bx+c 的图象与 x 轴有____ 个交点,坐标是______.方程 ax2+bx+c=0 的根是______.
1
(1,0)
x = 1
问题3 如果方程ax2+bx+c=0 (a≠0)没有实数根,那么函数y=ax2+bx+c的图象与 x轴有______个交点;
不等式ax2+bx+c<0的解集是多少?
0
解:当a>0时, ax2+bx+c<0无解;当a<0时, ax2+bx+c<0的解集是一切实数.
新知探究
归纳总结:
二次函数y=ax2+bx+c的图象与x轴交点的坐标与一元二次不等式的关系
二次函数y=ax2+bx+c的图象与x轴交点 a>0 a<0
有两个交点x1,x2 (x1<x2)
有一个交点x0
没有交点
y<0,x1<x<x2.
y>0,x2<x或x<x1
y>0,x1<x<x2.
y<0,x2<x或x<x1
y>0,x0之外的所有实数;y<0,无解
y<0,x0之外的所有实数;y>0,无解
y>0,所有实数;y<0,无解
y<0,所有实数;y>0,无解
课堂小结
二次函数图象
由图象与x轴的交点位置,
判断方程根的近似值
一元二次方程的根
一元二次不等式的解集
课堂训练
1.(2023秋 咸宁期中)方程2x2+x-2=0的近似根可以看作是下列哪两个函数图象交点的横坐标( )
A.y=2x2和y=x-2 B.y=2x2+x和y=2
C.y=2x2-2和y=x D.y=-2x2和y=x+2
B
课堂训练
2.(2023秋 怀远县期中)下表列出了函数y=ax2+bx+c(a≠0)中自变量x与函数y的部分对应值.根据表中数据,判断一元二次方程ax2+bx+c=0(a≠0)的一个解在哪两个相邻的整数之间( )
A.1与2之间 B.-2与-1之间 C.-1与0之间 D.0与1之间
D
课堂训练
3.(2023 东平县校级模拟)如图,二次函数y=ax2+bx+c的部分图象与y轴的交点为(0,3),它的对称轴为直线x=1,则下列结论中:
①c=3;②2a+b=0;③8a-b+c>0;
④方程ax2+bx+c=0的其中一个根在2,3之间.
正确的有 (填序号).
①②④
课堂训练
4.(2023 泰安一模)已知二次函数y=ax2+bx+2的图象(a、b是常数)与y轴交于点A,点A与点B关于抛物线的对称轴对称,且点C(x1,y1),D(x2,y2)在该函数图象上.二次函数y=ax2+bx+2中(b、c是常数)的自变量x与函数值y的部分对应值如表:
下列结论:①点B的坐标是(2,2);②这个函数的最大值大于5;③ax2+bx=-1有一个根在4与5之间;④当0<x1<1,4<x2<5时,y1>y2.其中正确的为 .(将所有正确结论的序号都填入)
②③④
课堂训练
5. (2023秋 怀远县期中)二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象回答下列问题.
(1)写出方程ax2+bx+c=0的根;
(2)写出不等式ax2+bx+c<0的解集;
(3)若方程ax2+bx+c=k无实数根,写出k的取值范围.
解:(1)观察图象可知,方程ax2+bx+c=0的根,即为抛物线与x轴交点的横坐标.∴x1=0,x2=2.
(2)观察图象可知:不等式ax2+bx+c<0的解集为x<0或x>2.
(3)由图象可知,k>2时,方程ax2+bx+c=k无实数根.
