3.7 切线长定理 课件(共22张PPT)2024-2025学年数学北师大版九年级下册
文档属性
| 名称 | 3.7 切线长定理 课件(共22张PPT)2024-2025学年数学北师大版九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 494.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-13 00:00:00 | ||
图片预览




文档简介
(共22张PPT)
第三章 圆
7 切线长定理
北师大版-数学-九年级下册
学习目标
1.理解切线长的概念,掌握切线长定理;
2.学会运用切线长定理解有关问题.
【重点】理解切线长的定义.
【难点】掌握切线长定理并能运用切线长定理解决问题.
新课导入
2、什么叫切线的判定定理?
过半径外端且垂直于这条半径的直线是圆的切线.
1、什么是切线的性质定理?
圆的切线垂直于过切点的半径.
新课导入
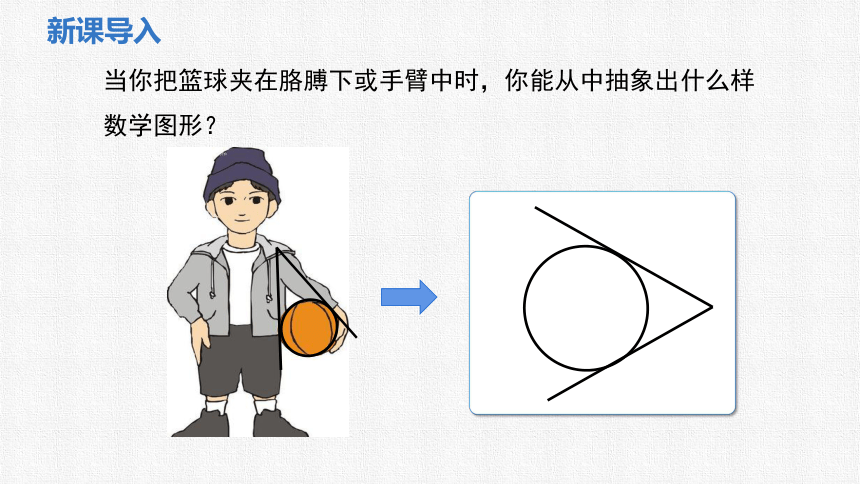
当你把篮球夹在胳膊下或手臂中时,你能从中抽象出什么样数学图形?
新知探究
知识点 切线长定理
1
B
A
过圆外一点画圆的切线,你能画出几条?试试看.
O
P
新知探究
知识点 切线长定理
1
A
B
O
P
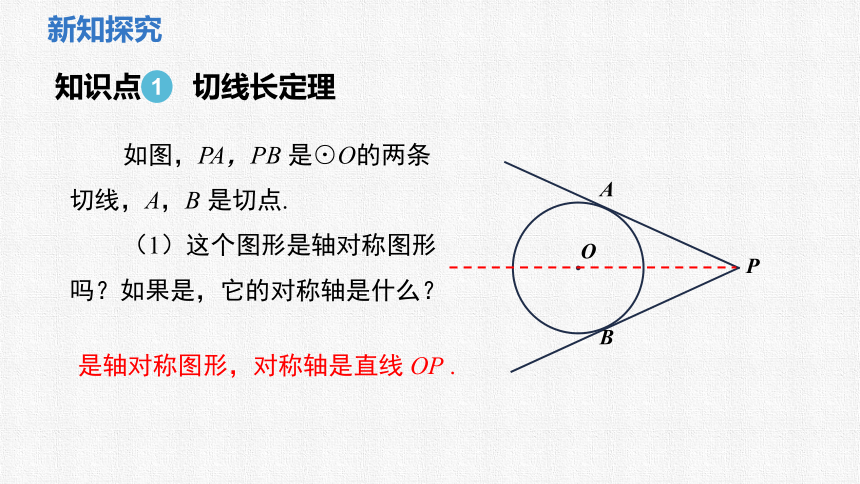
如图,PA,PB 是⊙O的两条切线,A,B 是切点.
(1)这个图形是轴对称图形吗?如果是,它的对称轴是什么?
是轴对称图形,对称轴是直线 OP .
新知探究
知识点 切线长定理
1
A
B
O
P
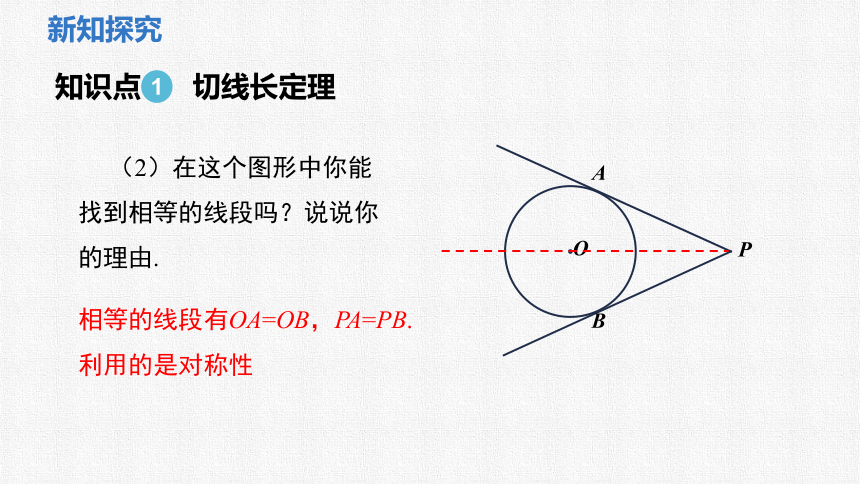
(2)在这个图形中你能找到相等的线段吗?说说你的理由.
相等的线段有OA=OB,PA=PB.利用的是对称性
新知探究
知识点 切线长定理
1
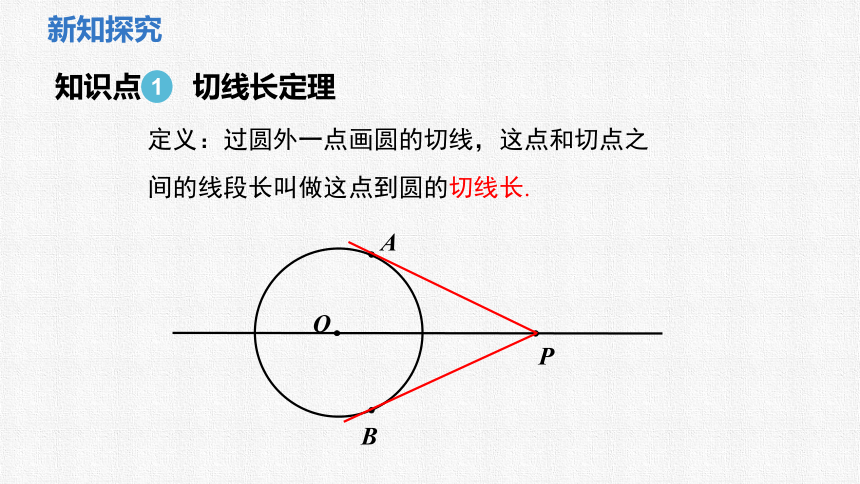
定义:过圆外一点画圆的切线,这点和切点之间的线段长叫做这点到圆的切线长.
O
P
A
B
新知探究
知识点 切线长定理
1
O
P
A
B
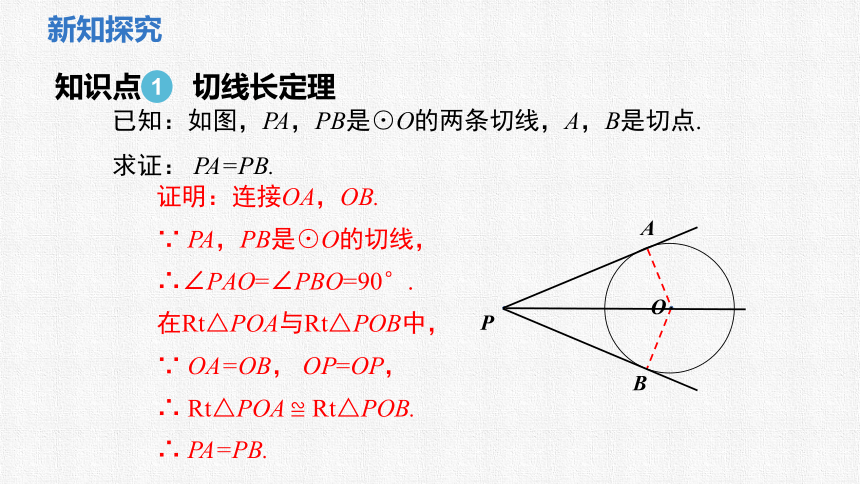
证明:连接OA,OB.
∵ PA,PB是⊙O的切线,
∴∠PAO=∠PBO=90°.
在Rt△POA与Rt△POB中,
∵ OA=OB, OP=OP,
∴ Rt△POA ≌ Rt△POB.
∴ PA=PB.
已知:如图,PA,PB是⊙O的两条切线,A,B是切点.
求证: PA=PB.
新知探究
知识点 切线长定理
1
切线长定理
∵ PA,PB分别切⊙O于点A,B,∴ PA=PB , OP平分∠APB.
过圆外一点画圆的两条切线,它们的切线长相等.
几何语言:
O
P
A
B
新知探究
知识点 切线长定理
1
根据Rt△AOP与Rt△BOP全等,我们还可以得到其他一些什么结论?
O
P
A
B
还可以得到:∠OPA=∠OPB,
∠POA=∠POB.
从而切线长定理可拓展为:过圆外一点画圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.
新知探究
知识点 切线长定理
1
B
P
O
A
练习: PA,PB 是 ⊙O 的两条切线,A,B 是切点,OA=3.
(1) 若 AP = 4,则 OP = ;
(2) 若 ∠BPA = 60°,则 OP = .
5
6
新知探究
知识点 外切四边形
2
如图,四边形 ABCD 的四条边都与⊙O 相切,图中的线段之间有哪些等量关系?
A
B
O
C
D
DE=DH,
AG=AH,
BG=BF,
CE=CF.
G
F
E
H
新知探究
知识点 外切四边形
2
想一想:将上面四个等式左右两边分别相加,我们能得出什么结论?
圆外切四边形的性质:
圆外切四边形的两组对边和相等.
AG+BG+DE+CE=AH+BF+DH+CF
A
B
D
G
F
E
H
O
C
所以AB+CD = AD+BC
课堂小结
切线长
切线长定理
作用
图形的轴对称性
原理
提供了证线段和
角相等的新方法
外切四边形
圆外切四边形的两组对边和相等
课堂训练
20°
4
1. 如图,PA,PB 是 ⊙O 的两条切线,切点分别是 A,B,如果 AP=4,∠APB= 40° ,则 ∠APO= ,PB= .
课堂训练
2. 如图,PA、PB 是 ⊙O 的切线,切点分别为 A、B,点 C 在 ⊙O 上,如果 ∠ACB=70°,那么 ∠OPA 的度数是_____°.
20
课堂训练
3. 如图,PA、PB 是 ⊙O 的两条切线,切点为 A、B,
∠P= 50°,点 C 是 ⊙O 上异于 A、B 的点,则∠ACB= .
65°或115°
B
P
O
A
课堂训练
4. 下列说法正确的是( )
A.过任意一点总可以作圆的两条切线
B.圆的切线长就是圆的切线的长度
C.过圆外一点所画的圆的两条切线长相等
D.过圆外一点所画的圆的切线长一定大于圆的半径
C
课堂训练
5. 如图,PA切⊙O于A,PB切⊙O于B,连接OP,AB.
下列结论不一定正确的是( )
A.PA=PB
B.OP垂直平分AB
C.∠OPA=∠OPB
D.PA=AB
D
课堂训练
6. 如图,PA和PB是⊙O的切线,点A和B是切点,AC是⊙O的直径,已知∠P=40°,则∠ACB的大小是( )
A.60°
B.65°
C.70°
D.75°
C
课堂训练
7.如图,PA,PB是⊙O的两条切线,A,B为切点,AC是⊙O的直径,已知∠BAC=35°,求∠P的度数.
解:∵OA=OB,
∴∠BAC=∠OBA=35°,
∴∠AOB=110°.
∵PA,PB是⊙O的两条切线,
∴∠PAO=∠PBO=90°,
∴∠P=360°-(∠AOB+∠PAO+∠PBO)=360°-
(110°+90°+90°)=70°
第三章 圆
7 切线长定理
北师大版-数学-九年级下册
学习目标
1.理解切线长的概念,掌握切线长定理;
2.学会运用切线长定理解有关问题.
【重点】理解切线长的定义.
【难点】掌握切线长定理并能运用切线长定理解决问题.
新课导入
2、什么叫切线的判定定理?
过半径外端且垂直于这条半径的直线是圆的切线.
1、什么是切线的性质定理?
圆的切线垂直于过切点的半径.
新课导入
当你把篮球夹在胳膊下或手臂中时,你能从中抽象出什么样数学图形?
新知探究
知识点 切线长定理
1
B
A
过圆外一点画圆的切线,你能画出几条?试试看.
O
P
新知探究
知识点 切线长定理
1
A
B
O
P
如图,PA,PB 是⊙O的两条切线,A,B 是切点.
(1)这个图形是轴对称图形吗?如果是,它的对称轴是什么?
是轴对称图形,对称轴是直线 OP .
新知探究
知识点 切线长定理
1
A
B
O
P
(2)在这个图形中你能找到相等的线段吗?说说你的理由.
相等的线段有OA=OB,PA=PB.利用的是对称性
新知探究
知识点 切线长定理
1
定义:过圆外一点画圆的切线,这点和切点之间的线段长叫做这点到圆的切线长.
O
P
A
B
新知探究
知识点 切线长定理
1
O
P
A
B
证明:连接OA,OB.
∵ PA,PB是⊙O的切线,
∴∠PAO=∠PBO=90°.
在Rt△POA与Rt△POB中,
∵ OA=OB, OP=OP,
∴ Rt△POA ≌ Rt△POB.
∴ PA=PB.
已知:如图,PA,PB是⊙O的两条切线,A,B是切点.
求证: PA=PB.
新知探究
知识点 切线长定理
1
切线长定理
∵ PA,PB分别切⊙O于点A,B,∴ PA=PB , OP平分∠APB.
过圆外一点画圆的两条切线,它们的切线长相等.
几何语言:
O
P
A
B
新知探究
知识点 切线长定理
1
根据Rt△AOP与Rt△BOP全等,我们还可以得到其他一些什么结论?
O
P
A
B
还可以得到:∠OPA=∠OPB,
∠POA=∠POB.
从而切线长定理可拓展为:过圆外一点画圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.
新知探究
知识点 切线长定理
1
B
P
O
A
练习: PA,PB 是 ⊙O 的两条切线,A,B 是切点,OA=3.
(1) 若 AP = 4,则 OP = ;
(2) 若 ∠BPA = 60°,则 OP = .
5
6
新知探究
知识点 外切四边形
2
如图,四边形 ABCD 的四条边都与⊙O 相切,图中的线段之间有哪些等量关系?
A
B
O
C
D
DE=DH,
AG=AH,
BG=BF,
CE=CF.
G
F
E
H
新知探究
知识点 外切四边形
2
想一想:将上面四个等式左右两边分别相加,我们能得出什么结论?
圆外切四边形的性质:
圆外切四边形的两组对边和相等.
AG+BG+DE+CE=AH+BF+DH+CF
A
B
D
G
F
E
H
O
C
所以AB+CD = AD+BC
课堂小结
切线长
切线长定理
作用
图形的轴对称性
原理
提供了证线段和
角相等的新方法
外切四边形
圆外切四边形的两组对边和相等
课堂训练
20°
4
1. 如图,PA,PB 是 ⊙O 的两条切线,切点分别是 A,B,如果 AP=4,∠APB= 40° ,则 ∠APO= ,PB= .
课堂训练
2. 如图,PA、PB 是 ⊙O 的切线,切点分别为 A、B,点 C 在 ⊙O 上,如果 ∠ACB=70°,那么 ∠OPA 的度数是_____°.
20
课堂训练
3. 如图,PA、PB 是 ⊙O 的两条切线,切点为 A、B,
∠P= 50°,点 C 是 ⊙O 上异于 A、B 的点,则∠ACB= .
65°或115°
B
P
O
A
课堂训练
4. 下列说法正确的是( )
A.过任意一点总可以作圆的两条切线
B.圆的切线长就是圆的切线的长度
C.过圆外一点所画的圆的两条切线长相等
D.过圆外一点所画的圆的切线长一定大于圆的半径
C
课堂训练
5. 如图,PA切⊙O于A,PB切⊙O于B,连接OP,AB.
下列结论不一定正确的是( )
A.PA=PB
B.OP垂直平分AB
C.∠OPA=∠OPB
D.PA=AB
D
课堂训练
6. 如图,PA和PB是⊙O的切线,点A和B是切点,AC是⊙O的直径,已知∠P=40°,则∠ACB的大小是( )
A.60°
B.65°
C.70°
D.75°
C
课堂训练
7.如图,PA,PB是⊙O的两条切线,A,B为切点,AC是⊙O的直径,已知∠BAC=35°,求∠P的度数.
解:∵OA=OB,
∴∠BAC=∠OBA=35°,
∴∠AOB=110°.
∵PA,PB是⊙O的两条切线,
∴∠PAO=∠PBO=90°,
∴∠P=360°-(∠AOB+∠PAO+∠PBO)=360°-
(110°+90°+90°)=70°
