苏科版数学八年级下册实验手册培训课件 数学实验手册解读与思考 (共116张PPT)
文档属性
| 名称 | 苏科版数学八年级下册实验手册培训课件 数学实验手册解读与思考 (共116张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-03 00:00:00 | ||
图片预览








文档简介
课件116张PPT。数学实验手册解读与思考 南京市第二十九中学初中部 侯正永 初中数学实验概念:
??? 数学实验是学生动手动脑,以“做”为支架的数学教与学的活动方式,是在教师的引导下,学生运用有关工具,通过具体操作在认知和非认知因素参与下,进行的一种发现数学结论、理解数学知识、验证数学结论的数学活动.1.核心是手脑并用、启思明理;
2.数学实验是一个环节,不是整个的教学过程,实验不能替代逻辑推理证明; 利用工具通过操作来完成;
3.数学实验是需要教师的引导和启发,需要教师有意识的设计,需预设实验目标. ? 基本理念:
做数学,让学生享受完整的数学学习过程. 基本思想:
手脑协同,启思明理. 初中数学实验的形态:
以“做”为支架的教与学的方式.全册共15个实验主题一、总体分布情况第7章 数据的收集、整理、描述
实验1
第8章 认识概率
实验2
第9章 中心对称图形——平行四边形
实验3——实验10,共8个
第10章 分式
实验11
第11章 反比例函数
实验12 实验13
第12章 二次根式
实验14
综合 实验15
初中数学实验可以分为六种基本类型,即实物验证型、实物理解型、实物探索型、计算机验证型、计算机理解型以及计算机探索型.(见董主任、魏玉华论文《浅析初中数学实验的基本类型》)
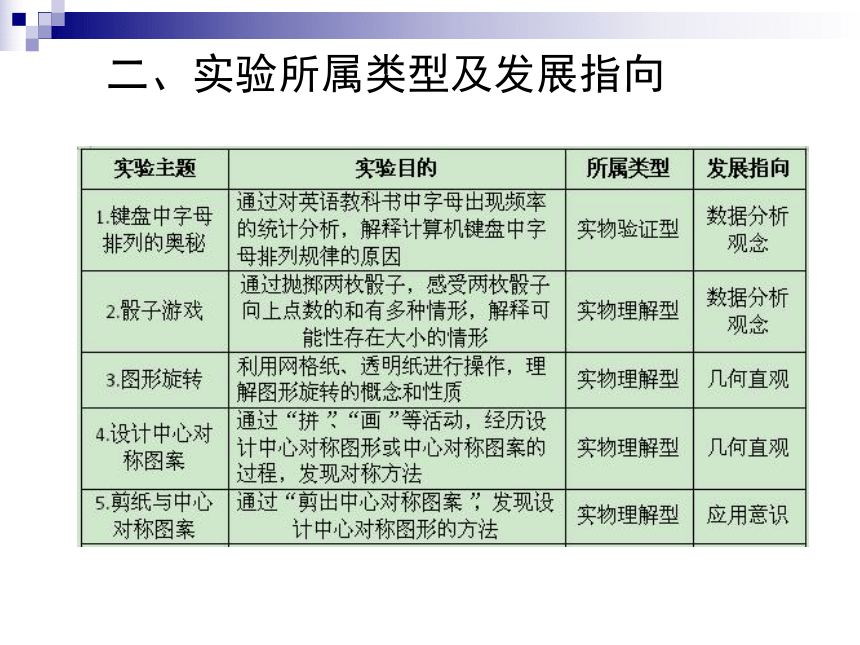
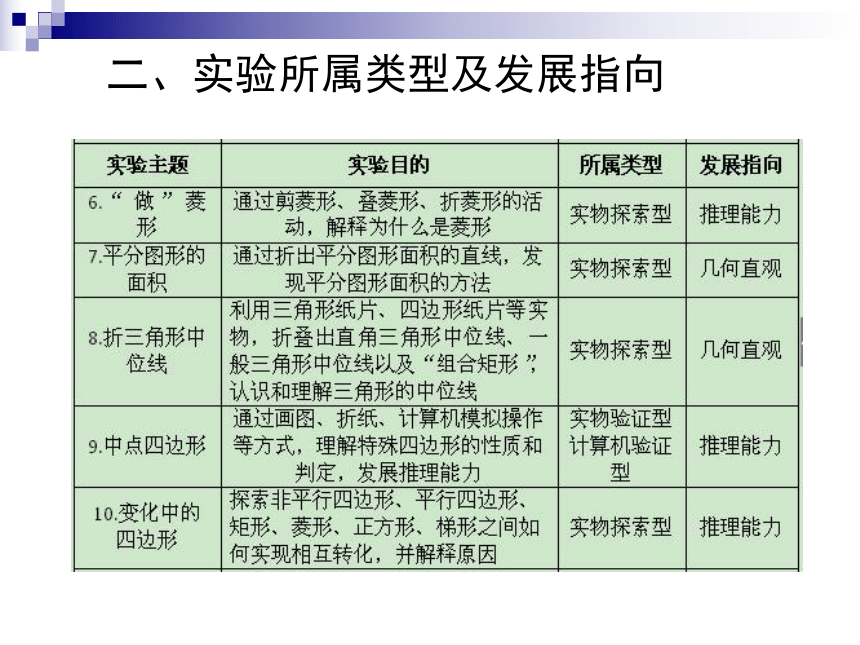
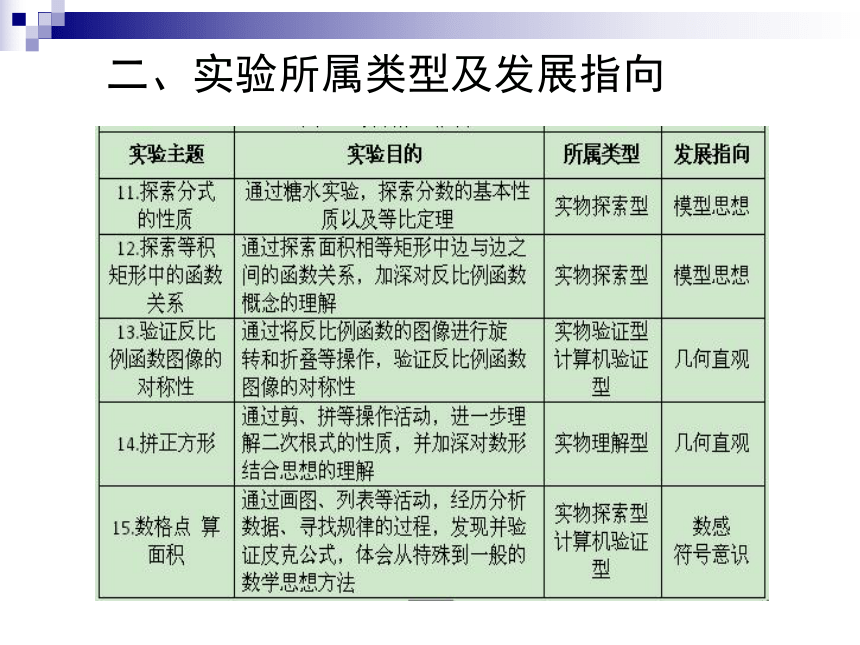
发展指向具体指该实验主题所指向的初中数学学科核心概念:数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力、模型思想、应用意识、创新意识。二、实验所属类型及发展指向二、实验所属类型及发展指向二、实验所属类型及发展指向二、实验所属类型及发展指向二、实验所属类型及发展指向从使用工具来看,实物13.5个(12+0.5+0.5+0.5);
计算机1.5个(0.5+0.5)。
从所属类型来看,实物验证型2.5个(1+0.5+0.5+0.5);
实物理解型5个;
实物探索型6个;
计算机验证型1.5个(0.5+0.5+0.5)。
从发展指向来看,数感0.5个;符号意识0.5;
几何直观6个;数据分析观念2个;
推理能力3个;模型思想2个;
应用意识1个。
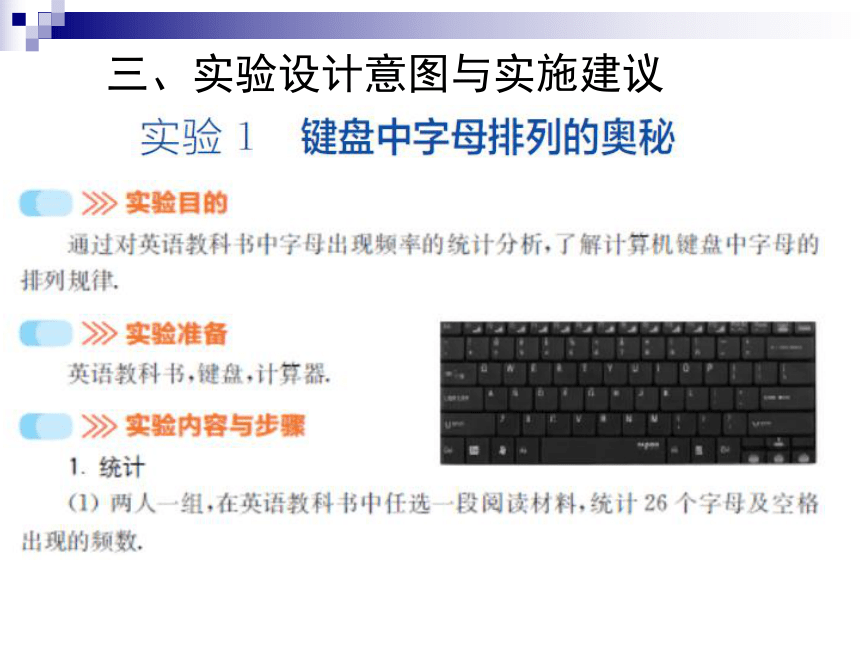
三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议 实验1 键盘中字母排列的奥秘
1.直观呈现键盘
目的:便于观察
2.统计:
先小组再全班,样本数据越大效果越好。
3.统计方法:
建议利用word查找替换功能,
三、实验设计意图与实施建议 实验1 键盘中字母排列的奥秘
3.统计方法:
建议利用
word查找替换功能,
三、实验设计意图与实施建议 实验1 键盘中字母排列的奥秘
4.统计结果:
有人曾做过大量统计,把字母和空格键出现的频率由大到小排列为:空格键,E,T,O,A,N,I,R,S,H,D,L,C,F,U,M,P,W,Y,G,B,V,K,X,J,Q,Z.
(见侯正永论文《在数学实验中发展学生的数据分析观念》,中国数学教育2015年第11期)
5.思考交流:
冰冷的数据;
火热的思考!
三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议 实验2 骰子游戏
1.规定次数or规定时间:
从原来规定小组抛掷30次改为现在的限时5min!
(定量——不定量;封闭——开放;被动——主动;
完成任务——引入竞争机制……)
2.填表与绘图
先小组再全班。
小组绘图前需将频数
转化为频率!
三、实验设计意图与实施建议 实验2 骰子游戏
3.成果展示:
建议将各小组的条形统计图粘贴在展示板上!
(充分激发学生的参与欲和展示欲……)
三、实验设计意图与实施建议 实验2 骰子游戏
3.成果展示:
建议将各小组的条形统计图粘贴在展示板上!
(充分激发学生的参与欲和展示欲……)
三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议 实验3 图形旋转
1.从给定旋转中心到先确定旋转中心:
(铺设台阶,拾级而上)
三、实验设计意图与实施建议 实验3 图形旋转
1.从给定旋转中心到先确定旋转中心——发现性质
(引发思考:旋转中心是如何确定的?)
一次旋转
两次平移三、实验设计意图与实施建议 实验3 图形旋转
2.从网格纸到去掉网格纸——验证性质
(利用透明纸,建议学生先在透明纸上描出三角形ABC,再尝试旋转)
从无序尝试走向有序思考!三、实验设计意图与实施建议 实验3 图形旋转
2.从网格纸到去掉网格纸:
(利用透明纸,建议学生先在透明纸上描出三角形ABC,再尝试旋转,最后进行验证)
从无序尝试走向有序思考! 对应点连线段的垂直平分线的交点,即为旋转中心。三、实验设计意图与实施建议 实验3 图形旋转
3.从借助透明纸旋转到尺规画图——应用性质
(1.利用方格纸;2.利用圆规、量角器)
三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议 实验4 设计中心对称图案
1.简单拼图——方法不唯一
(1.边重合;2.顶点重合)
建议:将学生的不同拼法展示在黑板上。三、实验设计意图与实施建议 实验4 设计中心对称图案
2.较为复杂拼图——引导思考
(关键在于两个三角形处于中心对称的位置)
建议:将学生的不同拼法展示在黑板上。三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议 实验5 剪纸与中心对称图案
1.两次折叠,完全重合——剪出既是轴对称又是中心对称的图案
(两条折痕互相垂直——旋转)
隐含:两次翻折相当于一次旋转!
建议:将学生仿照上述两例剪出的图案进
行展示。三、实验设计意图与实施建议 实验5 剪纸与中心对称图案
2.两次折叠,部分重合——剪出中心对称但不是轴对称的图案
(两条折痕互相垂直,边上两次重合——旋转)
隐含:两次翻折相当于一次旋转!
建议:将学生仿照上述两例剪出的图案进
行展示。三、实验设计意图与实施建议 实验5 剪纸与中心对称图案
2.两次折叠,部分重合——剪出中心对称但不是轴对称的图案
(两条折痕互相垂直,有两部分两次重合——旋转)
仍然隐含:两次翻折相当于一次旋转!
强烈建议:这个剪纸让有兴趣的学生课外完成。三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议 实验6 “做”菱形
1.为什么“做”要加引号?
一方面,是“剪”“叠”“折”的统称;
另一方面,是依据菱形的判定而“做”成的。
2.发展推理能力
剪出菱形——利用两条对角线互相垂直平分;
叠出菱形——利用四条边相等;
折出菱形——利用一组邻边相等的平行四边形;利用四条边相等。
建议:上述各种情形也都可以先说明所得到的四边形是平行四边形,再说明是菱形。建议让学生先观察折痕的位置关系以及数量关系,帮助学生会用数学的语言进行表达!三、实验设计意图与实施建议 实验6 “做”菱形
剪出菱形——利用两条对角线互相垂直平分
建议:让学生思考如何利用这张矩形纸片用另外的方法剪出菱形?三、实验设计意图与实施建议 实验6 “做”菱形
叠出菱形——利用四条边相等
建议:学生思考重叠部分何时面积最大与何时面积最小时,请学生先行操作,再说明理由!三、实验设计意图与实施建议 实验6 “做”菱形
折出菱形——利用一组邻边相等的平行四边形
建议:让学生先看懂图示折叠方式,再通过观察折痕之间的位置关系和数量关系进行说理!三、实验设计意图与实施建议 实验6 “做”菱形
折出菱形——利用一组邻边相等的平行四边形;利用四条边相等
建议:让学生先看懂图示折叠方式并独立操作之后,再通过观察折痕之间的位置关系和数量关系进行说理!三、实验设计意图与实施建议 实验6 “做”菱形
折出菱形——利用一组邻边相等的平行四边形;利用四条边相等
建议:让学生先看懂图示折叠方式并独立操作之后,再通过观察折痕之间的位置关系和数量关系进行说理!三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议 实验7 平分图形的面积
1.平分一组特殊的平行四边形的面积
建议:除沿对角线折叠以外,让学生思考平分图形面积的直线还有吗?最后能得到一般结论:过对称中心的任意一条直线均可平分该特殊平行四边形的面积。三、实验设计意图与实施建议 实验7 平分图形的面积
2.平分组合图形的面积
注:第一个图形折叠成两个矩形,过两个矩形对称中心的直线即是平分该组合图形面积的直线;而第二个图形找出矩形的对称中心并不难,然后尝试过矩形的对称中心折叠使得圆被分成的两条弧度重合即可。三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议 实验8 折三角形中位线
1.折三角形中位线——直角三角形和非直角三角形
注:为什么问“非重叠部分是等腰三角形吗?”,主要为再次折叠做铺垫。折非直角三角形中位线隐含转化思想!当然,先折出三边的中点,再折出中位线也是可以的!三、实验设计意图与实施建议 实验8 折三角形中位线
2.折“组合矩形”——承接折三角形的中位线
注:这里的折叠就用到了“非重叠部分是等腰三角形”这一结论!
建议:让学生通过折叠,自己发现中位线定理并说理表达!三、实验设计意图与实施建议 实验8 折三角形中位线
3.画格点三角形——逆向思维的体现
建议:让学生自己先行思考再通过折叠验证,自悟要使折叠成的组合矩形为正方形,必须满足“三角形一边上的高于这边相等”这一条件!三、实验设计意图与实施建议 实验8 折三角形中位线
4.延伸——从三角形到四边形
建议:引导学生从菱形出发进行思考——原四边形的两条对角线需互相垂直!三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议实验9 中点四边形
1.给出定义——非常必要
课本中没有“中点四边形”这一定义,平时只是约定俗成的,这里需要也有必要先行定义。
2.实验路径——
猜想-操作-验证
(从特殊四边形入手,
见右图,附录中有图)
建议:本节课最好与实验8一起进行,因为这是在实验8的基础上的拓展!三、实验设计意图与实施建议 实验9 中点四边形
3.一般四边形的中点四边形——重在思考
中点四边形由原四边形中的什么元素决定的?
实验路径:画图-观察-验证-度量-思考-发现
建议:教师明确要求后,让学生充分活动,教师切勿包办代替,即使发现不了与对角线之间的关系也不要紧!三、实验设计意图与实施建议 实验9 中点四边形
4.计算机模拟操作——精确发现前述结论
(利用几何画板的精确度量功能)
建议:对于几何画板不太熟悉的班级,该部分可由教师进行演示实验,学生观察发现,进而进行逆向思考!三、实验设计意图与实施建议 实验9 中点四边形
5.拓展延伸——从边上中点过度到边和对角线的中点
(渗透转化思想,属思维性实验)
建议:本环节重在引导学生观察与思考,发现此时的四边形EFGH的形状取决于原四边形中AB、CD两边的数量及位置关系!三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议 实验10 变化中的四边形
1.设计意图——四边形这一章的复习而设置,通过操作进一步厘清四边形之间的关系
(从四边形到特殊四边形的转化)
2.实验路径——
操作-观察-思考-发现
3.实验材料——
橡皮筋、螺钉、薄木片(或雪糕棒)等
建议:本实验要先行制作学具,可以教师实验前制作好供学生使用,也可以在教师指导下让学生制作实验工具!三、实验设计意图与实施建议 实验10 变化中的四边形
4.利用橡皮筋——调整对角线进行思考与发现
(从四边形到特殊四边形的转化)
建议:这个实验工具可以在教师指导下让学生制作,然后进行操作实验,发现四边形之间的关系!三、实验设计意图与实施建议 实验10 变化中的四边形
5.利用螺钉——调整边的长度进行思考与发现
(仍然是从四边形到特殊四边形的转化)
建议:这个实验工具可以教师先行制作好,然后让学生分组进行操作实验,发现四边形之间的关系!三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议 实验11 探索分式的性质
1.糖水作为实验材料——也可以选用其他可以代替的材料——从具体模型到抽象的模型
(比如用带有颜色的墨水,近似浓度定义,虽然不是太准确,但可以说明问题)
建议:最好到化学实验室进行实验,烧杯、滴管等一应俱全!三、实验设计意图与实施建议 实验11 探索分式的性质
2.添加糖或水——感受甜度的变化
(从生活中糖水甜度的变化情况——引导学生用数学式子进行表述——不等式)
建议:不一定要真的尝尝,基于学生的生活经验是能够直观感受的,关键是如何用数学式子进行表述,教师需要做铺垫性的引导!三、实验设计意图与实施建议 实验11 探索分式的性质
3.配置糖水——发现分式性质
一方面可以发现:分式的分子分母同时乘以或除以同一个数,分式的值不变(这里指甜度不变);
另一方面也可以发现:等比定理。
建议:操作这个实验时,最好先将一大杯分成等分的小杯;再将等分的小杯倒在一次合成一个大杯,学生容易联想到分式的性质!最后的拓展迁移,宜引导学生从数学内部进行思考!三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议 实验12 探索等积矩形中的函数关系
1.操作与度量并填表——发现所有矩形的长与宽的积都是定值,即所有矩形的面积都相等(旨在发现矩形长与宽之间存在函数关系)
注:附录中给出的10个矩形,其中的边长不都是整数,含有小数,只是让学生感受函数的连续性关系!三、实验设计意图与实施建议 实验12 探索等积矩形中的函数关系
2.用光滑的线联接
矩形右上角的顶点——
发现反比例的
图像是双曲线
(效果非常明显)
注:附录中给出的10个矩形,其中的边长不都是整数,含有小数,只是让学生感受函数的连续性关系!三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议 实验13 验证反比例函数图像的对称性
1.实验目的——验证反比例函数图像的轴对称性和中心对称性
2.实验路径——利用透明纸折叠或旋转-利用计算机作对称点-观察与发现
建议:利用透明纸进行操作——折叠或旋转,可以由学生利用附录中的材料进行,发现对称性;可在教师指导下利用计算机进行相关操作并验证!三、实验设计意图与实施建议 实验13 验证反比例函数图像的对称性
3.验证中心对称性——旋转、找对称点、观察
注:附录中已经配备了透明纸,需要先行固定再旋转!三、实验设计意图与实施建议 实验13 验证反比例函数图像的对称性
3.验证中心对
称性——
旋转、找对称点、
观察
注:先将坐标原点标记为中心,再将P点旋转180度!三、实验设计意图与实施建议 实验13 验证反比例函数图像的对称性
4.验证轴对称性——折叠、找对称点、观察
注:附录中已经配备了透明纸!三、实验设计意图与实施建议 实验13 验证反比例函数图像的对称性
4.验证轴对称性——折叠、找对称点、观察
注:利用附录中已经配备了透明纸!三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议 实验14 拼正方形
1.利用方格纸拼正方形——先思考,再剪
建议:教师先引导学生思考,如果拼成正方形,面积为多少?边长呢?三、实验设计意图与实施建议 实验14 拼正方形
2.利用方格纸画矩形——先画,再计算(通过两条途径进行计算)
3.通过计算拼正方形——先计算,再剪拼
注:一方面,矩形的面积为10;另一方面,矩形的面积应为
第二个图形的等式为三、实验设计意图与实施建议 实验14 拼正方形
4.剪拼组合图形成正方形——先思考,再尝试剪拼
建议:教师要先引导学生思考,拼成的大正方形的面积如何表示?边长如何表示?然后引导学生自己构造线段
三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议 实验15 数格点 算面积
1.控制变量——从N=0,N=1,N=2……
三、实验设计意图与实施建议 实验15 数格点 算面积
1.控制变量——从N=0,N=1,N=2……
三、实验设计意图与实施建议 实验15 数格点 算面积
2.发现规律——填表,发现面积S与边上的格点数L之间的关系
建议:对于几何画板比较熟悉的班级,可以利用几何画板的度量功能,直接得到图形面积!三、实验设计意图与实施建议 实验15 数格点 算面积
2.发现规律——填表,发现面积S与边上的格点数L之间的关系
建议:对于几何画板比较熟悉的班级,可以利用几何画板的度量功能,直接得到图形面积!三、实验设计意图与实施建议 实验15 数格点 算面积
3.发现公式——将四个式子进行比较,发现面积皮克公式
N=0 S=1/2L-1
N=1 S=1/2L
N=2 S=1/2L+1
N=3 S=1/2L+2
……
N=8 S=1/2L+7
S=1/2L+N-1三、实验设计意图与实施建议 实验15 数格点 算面积
4.实践证明——本实验主题并不难
注:小学五年级——《钉子板上的多边形》①②③④233.544678当多边形内有1枚钉子时,S= ___________n÷24781034.556当多边形内有2枚钉子时,S= _________n÷2+1当多边形内有a枚钉子时,S= _______ n÷2+a-1三、实验设计意图与实施建议 实验15 数格点 算面积
4.实践证明——本实验主题并不难
谢 谢 !
仅供参考!
2.数学实验是一个环节,不是整个的教学过程,实验不能替代逻辑推理证明; 利用工具通过操作来完成;
3.数学实验是需要教师的引导和启发,需要教师有意识的设计,需预设实验目标. ? 基本理念:
做数学,让学生享受完整的数学学习过程. 基本思想:
手脑协同,启思明理. 初中数学实验的形态:
以“做”为支架的教与学的方式.全册共15个实验主题一、总体分布情况第7章 数据的收集、整理、描述
实验1
第8章 认识概率
实验2
第9章 中心对称图形——平行四边形
实验3——实验10,共8个
第10章 分式
实验11
第11章 反比例函数
实验12 实验13
第12章 二次根式
实验14
综合 实验15
初中数学实验可以分为六种基本类型,即实物验证型、实物理解型、实物探索型、计算机验证型、计算机理解型以及计算机探索型.(见董主任、魏玉华论文《浅析初中数学实验的基本类型》)
发展指向具体指该实验主题所指向的初中数学学科核心概念:数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力、模型思想、应用意识、创新意识。二、实验所属类型及发展指向二、实验所属类型及发展指向二、实验所属类型及发展指向二、实验所属类型及发展指向二、实验所属类型及发展指向从使用工具来看,实物13.5个(12+0.5+0.5+0.5);
计算机1.5个(0.5+0.5)。
从所属类型来看,实物验证型2.5个(1+0.5+0.5+0.5);
实物理解型5个;
实物探索型6个;
计算机验证型1.5个(0.5+0.5+0.5)。
从发展指向来看,数感0.5个;符号意识0.5;
几何直观6个;数据分析观念2个;
推理能力3个;模型思想2个;
应用意识1个。
三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议 实验1 键盘中字母排列的奥秘
1.直观呈现键盘
目的:便于观察
2.统计:
先小组再全班,样本数据越大效果越好。
3.统计方法:
建议利用word查找替换功能,
三、实验设计意图与实施建议 实验1 键盘中字母排列的奥秘
3.统计方法:
建议利用
word查找替换功能,
三、实验设计意图与实施建议 实验1 键盘中字母排列的奥秘
4.统计结果:
有人曾做过大量统计,把字母和空格键出现的频率由大到小排列为:空格键,E,T,O,A,N,I,R,S,H,D,L,C,F,U,M,P,W,Y,G,B,V,K,X,J,Q,Z.
(见侯正永论文《在数学实验中发展学生的数据分析观念》,中国数学教育2015年第11期)
5.思考交流:
冰冷的数据;
火热的思考!
三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议 实验2 骰子游戏
1.规定次数or规定时间:
从原来规定小组抛掷30次改为现在的限时5min!
(定量——不定量;封闭——开放;被动——主动;
完成任务——引入竞争机制……)
2.填表与绘图
先小组再全班。
小组绘图前需将频数
转化为频率!
三、实验设计意图与实施建议 实验2 骰子游戏
3.成果展示:
建议将各小组的条形统计图粘贴在展示板上!
(充分激发学生的参与欲和展示欲……)
三、实验设计意图与实施建议 实验2 骰子游戏
3.成果展示:
建议将各小组的条形统计图粘贴在展示板上!
(充分激发学生的参与欲和展示欲……)
三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议 实验3 图形旋转
1.从给定旋转中心到先确定旋转中心:
(铺设台阶,拾级而上)
三、实验设计意图与实施建议 实验3 图形旋转
1.从给定旋转中心到先确定旋转中心——发现性质
(引发思考:旋转中心是如何确定的?)
一次旋转
两次平移三、实验设计意图与实施建议 实验3 图形旋转
2.从网格纸到去掉网格纸——验证性质
(利用透明纸,建议学生先在透明纸上描出三角形ABC,再尝试旋转)
从无序尝试走向有序思考!三、实验设计意图与实施建议 实验3 图形旋转
2.从网格纸到去掉网格纸:
(利用透明纸,建议学生先在透明纸上描出三角形ABC,再尝试旋转,最后进行验证)
从无序尝试走向有序思考! 对应点连线段的垂直平分线的交点,即为旋转中心。三、实验设计意图与实施建议 实验3 图形旋转
3.从借助透明纸旋转到尺规画图——应用性质
(1.利用方格纸;2.利用圆规、量角器)
三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议 实验4 设计中心对称图案
1.简单拼图——方法不唯一
(1.边重合;2.顶点重合)
建议:将学生的不同拼法展示在黑板上。三、实验设计意图与实施建议 实验4 设计中心对称图案
2.较为复杂拼图——引导思考
(关键在于两个三角形处于中心对称的位置)
建议:将学生的不同拼法展示在黑板上。三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议 实验5 剪纸与中心对称图案
1.两次折叠,完全重合——剪出既是轴对称又是中心对称的图案
(两条折痕互相垂直——旋转)
隐含:两次翻折相当于一次旋转!
建议:将学生仿照上述两例剪出的图案进
行展示。三、实验设计意图与实施建议 实验5 剪纸与中心对称图案
2.两次折叠,部分重合——剪出中心对称但不是轴对称的图案
(两条折痕互相垂直,边上两次重合——旋转)
隐含:两次翻折相当于一次旋转!
建议:将学生仿照上述两例剪出的图案进
行展示。三、实验设计意图与实施建议 实验5 剪纸与中心对称图案
2.两次折叠,部分重合——剪出中心对称但不是轴对称的图案
(两条折痕互相垂直,有两部分两次重合——旋转)
仍然隐含:两次翻折相当于一次旋转!
强烈建议:这个剪纸让有兴趣的学生课外完成。三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议 实验6 “做”菱形
1.为什么“做”要加引号?
一方面,是“剪”“叠”“折”的统称;
另一方面,是依据菱形的判定而“做”成的。
2.发展推理能力
剪出菱形——利用两条对角线互相垂直平分;
叠出菱形——利用四条边相等;
折出菱形——利用一组邻边相等的平行四边形;利用四条边相等。
建议:上述各种情形也都可以先说明所得到的四边形是平行四边形,再说明是菱形。建议让学生先观察折痕的位置关系以及数量关系,帮助学生会用数学的语言进行表达!三、实验设计意图与实施建议 实验6 “做”菱形
剪出菱形——利用两条对角线互相垂直平分
建议:让学生思考如何利用这张矩形纸片用另外的方法剪出菱形?三、实验设计意图与实施建议 实验6 “做”菱形
叠出菱形——利用四条边相等
建议:学生思考重叠部分何时面积最大与何时面积最小时,请学生先行操作,再说明理由!三、实验设计意图与实施建议 实验6 “做”菱形
折出菱形——利用一组邻边相等的平行四边形
建议:让学生先看懂图示折叠方式,再通过观察折痕之间的位置关系和数量关系进行说理!三、实验设计意图与实施建议 实验6 “做”菱形
折出菱形——利用一组邻边相等的平行四边形;利用四条边相等
建议:让学生先看懂图示折叠方式并独立操作之后,再通过观察折痕之间的位置关系和数量关系进行说理!三、实验设计意图与实施建议 实验6 “做”菱形
折出菱形——利用一组邻边相等的平行四边形;利用四条边相等
建议:让学生先看懂图示折叠方式并独立操作之后,再通过观察折痕之间的位置关系和数量关系进行说理!三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议 实验7 平分图形的面积
1.平分一组特殊的平行四边形的面积
建议:除沿对角线折叠以外,让学生思考平分图形面积的直线还有吗?最后能得到一般结论:过对称中心的任意一条直线均可平分该特殊平行四边形的面积。三、实验设计意图与实施建议 实验7 平分图形的面积
2.平分组合图形的面积
注:第一个图形折叠成两个矩形,过两个矩形对称中心的直线即是平分该组合图形面积的直线;而第二个图形找出矩形的对称中心并不难,然后尝试过矩形的对称中心折叠使得圆被分成的两条弧度重合即可。三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议 实验8 折三角形中位线
1.折三角形中位线——直角三角形和非直角三角形
注:为什么问“非重叠部分是等腰三角形吗?”,主要为再次折叠做铺垫。折非直角三角形中位线隐含转化思想!当然,先折出三边的中点,再折出中位线也是可以的!三、实验设计意图与实施建议 实验8 折三角形中位线
2.折“组合矩形”——承接折三角形的中位线
注:这里的折叠就用到了“非重叠部分是等腰三角形”这一结论!
建议:让学生通过折叠,自己发现中位线定理并说理表达!三、实验设计意图与实施建议 实验8 折三角形中位线
3.画格点三角形——逆向思维的体现
建议:让学生自己先行思考再通过折叠验证,自悟要使折叠成的组合矩形为正方形,必须满足“三角形一边上的高于这边相等”这一条件!三、实验设计意图与实施建议 实验8 折三角形中位线
4.延伸——从三角形到四边形
建议:引导学生从菱形出发进行思考——原四边形的两条对角线需互相垂直!三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议实验9 中点四边形
1.给出定义——非常必要
课本中没有“中点四边形”这一定义,平时只是约定俗成的,这里需要也有必要先行定义。
2.实验路径——
猜想-操作-验证
(从特殊四边形入手,
见右图,附录中有图)
建议:本节课最好与实验8一起进行,因为这是在实验8的基础上的拓展!三、实验设计意图与实施建议 实验9 中点四边形
3.一般四边形的中点四边形——重在思考
中点四边形由原四边形中的什么元素决定的?
实验路径:画图-观察-验证-度量-思考-发现
建议:教师明确要求后,让学生充分活动,教师切勿包办代替,即使发现不了与对角线之间的关系也不要紧!三、实验设计意图与实施建议 实验9 中点四边形
4.计算机模拟操作——精确发现前述结论
(利用几何画板的精确度量功能)
建议:对于几何画板不太熟悉的班级,该部分可由教师进行演示实验,学生观察发现,进而进行逆向思考!三、实验设计意图与实施建议 实验9 中点四边形
5.拓展延伸——从边上中点过度到边和对角线的中点
(渗透转化思想,属思维性实验)
建议:本环节重在引导学生观察与思考,发现此时的四边形EFGH的形状取决于原四边形中AB、CD两边的数量及位置关系!三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议 实验10 变化中的四边形
1.设计意图——四边形这一章的复习而设置,通过操作进一步厘清四边形之间的关系
(从四边形到特殊四边形的转化)
2.实验路径——
操作-观察-思考-发现
3.实验材料——
橡皮筋、螺钉、薄木片(或雪糕棒)等
建议:本实验要先行制作学具,可以教师实验前制作好供学生使用,也可以在教师指导下让学生制作实验工具!三、实验设计意图与实施建议 实验10 变化中的四边形
4.利用橡皮筋——调整对角线进行思考与发现
(从四边形到特殊四边形的转化)
建议:这个实验工具可以在教师指导下让学生制作,然后进行操作实验,发现四边形之间的关系!三、实验设计意图与实施建议 实验10 变化中的四边形
5.利用螺钉——调整边的长度进行思考与发现
(仍然是从四边形到特殊四边形的转化)
建议:这个实验工具可以教师先行制作好,然后让学生分组进行操作实验,发现四边形之间的关系!三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议 实验11 探索分式的性质
1.糖水作为实验材料——也可以选用其他可以代替的材料——从具体模型到抽象的模型
(比如用带有颜色的墨水,近似浓度定义,虽然不是太准确,但可以说明问题)
建议:最好到化学实验室进行实验,烧杯、滴管等一应俱全!三、实验设计意图与实施建议 实验11 探索分式的性质
2.添加糖或水——感受甜度的变化
(从生活中糖水甜度的变化情况——引导学生用数学式子进行表述——不等式)
建议:不一定要真的尝尝,基于学生的生活经验是能够直观感受的,关键是如何用数学式子进行表述,教师需要做铺垫性的引导!三、实验设计意图与实施建议 实验11 探索分式的性质
3.配置糖水——发现分式性质
一方面可以发现:分式的分子分母同时乘以或除以同一个数,分式的值不变(这里指甜度不变);
另一方面也可以发现:等比定理。
建议:操作这个实验时,最好先将一大杯分成等分的小杯;再将等分的小杯倒在一次合成一个大杯,学生容易联想到分式的性质!最后的拓展迁移,宜引导学生从数学内部进行思考!三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议 实验12 探索等积矩形中的函数关系
1.操作与度量并填表——发现所有矩形的长与宽的积都是定值,即所有矩形的面积都相等(旨在发现矩形长与宽之间存在函数关系)
注:附录中给出的10个矩形,其中的边长不都是整数,含有小数,只是让学生感受函数的连续性关系!三、实验设计意图与实施建议 实验12 探索等积矩形中的函数关系
2.用光滑的线联接
矩形右上角的顶点——
发现反比例的
图像是双曲线
(效果非常明显)
注:附录中给出的10个矩形,其中的边长不都是整数,含有小数,只是让学生感受函数的连续性关系!三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议 实验13 验证反比例函数图像的对称性
1.实验目的——验证反比例函数图像的轴对称性和中心对称性
2.实验路径——利用透明纸折叠或旋转-利用计算机作对称点-观察与发现
建议:利用透明纸进行操作——折叠或旋转,可以由学生利用附录中的材料进行,发现对称性;可在教师指导下利用计算机进行相关操作并验证!三、实验设计意图与实施建议 实验13 验证反比例函数图像的对称性
3.验证中心对称性——旋转、找对称点、观察
注:附录中已经配备了透明纸,需要先行固定再旋转!三、实验设计意图与实施建议 实验13 验证反比例函数图像的对称性
3.验证中心对
称性——
旋转、找对称点、
观察
注:先将坐标原点标记为中心,再将P点旋转180度!三、实验设计意图与实施建议 实验13 验证反比例函数图像的对称性
4.验证轴对称性——折叠、找对称点、观察
注:附录中已经配备了透明纸!三、实验设计意图与实施建议 实验13 验证反比例函数图像的对称性
4.验证轴对称性——折叠、找对称点、观察
注:利用附录中已经配备了透明纸!三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议 实验14 拼正方形
1.利用方格纸拼正方形——先思考,再剪
建议:教师先引导学生思考,如果拼成正方形,面积为多少?边长呢?三、实验设计意图与实施建议 实验14 拼正方形
2.利用方格纸画矩形——先画,再计算(通过两条途径进行计算)
3.通过计算拼正方形——先计算,再剪拼
注:一方面,矩形的面积为10;另一方面,矩形的面积应为
第二个图形的等式为三、实验设计意图与实施建议 实验14 拼正方形
4.剪拼组合图形成正方形——先思考,再尝试剪拼
建议:教师要先引导学生思考,拼成的大正方形的面积如何表示?边长如何表示?然后引导学生自己构造线段
三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议三、实验设计意图与实施建议 实验15 数格点 算面积
1.控制变量——从N=0,N=1,N=2……
三、实验设计意图与实施建议 实验15 数格点 算面积
1.控制变量——从N=0,N=1,N=2……
三、实验设计意图与实施建议 实验15 数格点 算面积
2.发现规律——填表,发现面积S与边上的格点数L之间的关系
建议:对于几何画板比较熟悉的班级,可以利用几何画板的度量功能,直接得到图形面积!三、实验设计意图与实施建议 实验15 数格点 算面积
2.发现规律——填表,发现面积S与边上的格点数L之间的关系
建议:对于几何画板比较熟悉的班级,可以利用几何画板的度量功能,直接得到图形面积!三、实验设计意图与实施建议 实验15 数格点 算面积
3.发现公式——将四个式子进行比较,发现面积皮克公式
N=0 S=1/2L-1
N=1 S=1/2L
N=2 S=1/2L+1
N=3 S=1/2L+2
……
N=8 S=1/2L+7
S=1/2L+N-1三、实验设计意图与实施建议 实验15 数格点 算面积
4.实践证明——本实验主题并不难
注:小学五年级——《钉子板上的多边形》①②③④233.544678当多边形内有1枚钉子时,S= ___________n÷24781034.556当多边形内有2枚钉子时,S= _________n÷2+1当多边形内有a枚钉子时,S= _______ n÷2+a-1三、实验设计意图与实施建议 实验15 数格点 算面积
4.实践证明——本实验主题并不难
谢 谢 !
仅供参考!
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
