7.1为什么要证明 课件(共25张PPT)
文档属性
| 名称 | 7.1为什么要证明 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-14 14:46:16 | ||
图片预览








文档简介
(共25张PPT)
第七章平行线的证明
7.1为什么要证明
北师大版 数学 八年级 上册
学习目标
1.初步体会观察、猜测得到的结论不一定正确.
2.通过探索,初步了解数字中推理的重要性.
3.初步了解要判定一个数学结论正确与否,需要进行有根有据的推理.
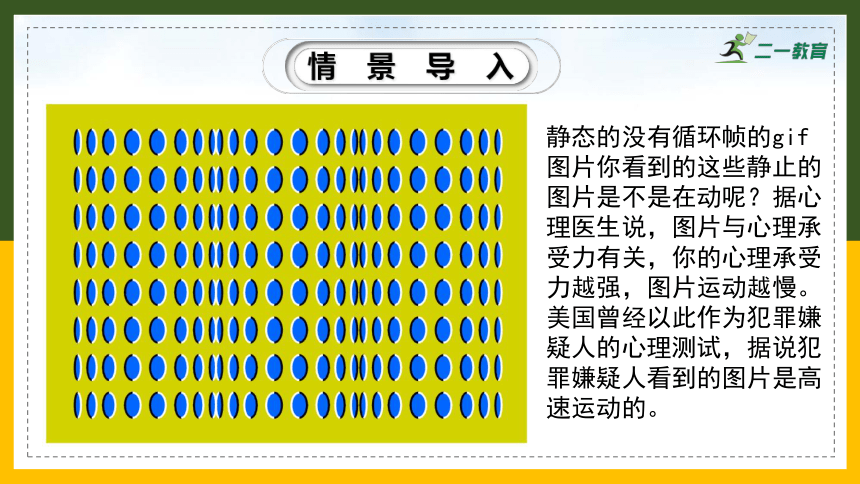
情景导入
静态的没有循环帧的gif图片你看到的这些静止的图片是不是在动呢?据心理医生说,图片与心理承受力有关,你的心理承受力越强,图片运动越慢。美国曾经以此作为犯罪嫌疑人的心理测试,据说犯罪嫌疑人看到的图片是高速运动的。
情景导入
【解析】英国视觉科学家、艺术家尼古拉斯·韦德向我们展示了他的弗雷泽螺旋幻觉的变体形式。虽然图形看起来像螺旋,但实际上它是一系列同心圆。
韦德螺旋:
这真是一个螺旋吗?
探索新知
数学的结论必须经过严格的论证
一
平行线:不敢相信图中的横线是平行的,不过它们就是平行线.
想一想:仅靠观察得到的结论一定正确吗?
不一定正确.
图中的横线是平行的吗?
探索新知
活动一:图1中两条线段a、b的长度相等吗?图2中的四边形是正方形吗?请你先观察,再设法检验你观察到的结论.
图1
b
a
图2
观察未必可靠
测量可以帮助我们验证猜想
探索新知
例1:当n=1,2,3,4,5时,代数式n2-3n+7的值是质数吗?你能肯定:对于所有的自然数,式子n2-3n+7的值都是质数吗?
解:当n=1,2,3,4,5时,n2-3n+7的值分别是5,5,7,11,17,全是质数.而当n=6时,n2-3n+7=62-18+7=25=52.
所以对于所有自然数,式子n2-3n+7的值不都是质数.
探索新知
【解后思考】判断一个数学结论是否正确,仅仅依靠经验、观察是不够的,必须给出严格的证明或实验验证.如此题,我们可以把1,2,3,4,5,6等自然数代入n2-3n+7中进行验证.
总结归纳
探索新知
1.许多猜想的结论,数学上的一些结论以及数学之外的其他事实,应当追其缘由,推理证明是非常必要的.
(1)要判断一个数学结论是否正确,仅仅依靠实验,观察、归纳是不够的,必须进行有根有据的证明.
(2)没有经过严格的推理,仅由若干特例归纳得出的结论可能潜藏着错误.
(3)对一个结论要肯定其是正确的,必须通过一步一步推理,论证才能下结论.
探索新知
2.要点精析:
(1)直觉有时会产生错误,不是永远可信的;
(2)图形的性质并不都是通过测量得出的;
(3)对少数具体例子的观察、测量或计算得出的结论,并不能保证一般情况下都成立;
(4)只有通过推理的方法研究问题,才能揭示问题的本质.
总结归纳
探索新知
检验数学结论的常用方法
二
【类型一】 实验验证
例2:线段a与线段b比较谁更长?
a
b
解:视觉上看,我们感觉线段a比线段b长一点,但用直尺来测量两条线段的长度,我们发现线段a与线段b一样长.
a
探索新知
【类型二】 举出反例
例3:当n为正整数时,代数式(n2-5n+5)2的值都等于1吗?
【分析】对于代数式(n2-5n+5)2,n的取值为正整数,要判断(n2-5n+5)2的值是否为1,可以先取值分别求出代数式的值.
探索新知
解:当n=1时,(n2-5n+5)2=12=1;
当n=2时,(n2-5n+5)2=(-1)2=1;
当n=3时,(n2-5n+5)2=(-1)2=1;
当n=4时,(n2-5n+5)2=12=1;
当n=5时,(n2-5n+5)2=52=25≠1.
所以当n为正整数时,(n2-5n+5)2不一定等于1.
探索新知
【类型三】 推理论证
例4:如图,从点O出发作出四条射线OA、OB、OC、OD,已知OA⊥OC,OB⊥OD.若∠BOC=30°,∠AOB和∠COD有什么关系呢?
【分析】∠AOB、∠COD均与∠BOC互余,根据角的和、差关系,可求∠AOB与∠COD的度数.通过计算发现∠AOB=∠COD.
探索新知
解:因为OA⊥OC,OB⊥OD,
所以∠AOC=∠BOD=90°.
因为∠BOC=30°,
所以∠AOB=∠AOC-∠BOC=90°-30°=60°,
∠COD=∠BOD-∠BOC=90°-30°=60°,
所以∠AOB=∠COD.
探索新知
总结归纳
1.检验数学结论常用的方法:
主要有:实验验证、举出反例、推理证明.实验验证是最基本的方法,它直接反映由具体到抽象、由特殊到一般的逻辑思维方法;举出反例常用于说明该数学结论不一定成立;推理证明是最可靠、最科学的方法,是我们要掌握的重点.实际上每一个正确的结论都需要我们进行严格的推理证明才能得出.检验数学结论的具体过程:观察、度量、实验→猜想归纳→结论→推理正确结论.
探索新知
总结归纳
2.应用:检验数学结论常用的三种方法的应用:
实验验证法常用于检验一些比较直观、简单的结论;举出反例法多用于验证某结论是不是正确的;推理证明主要用来进行严格的推理论证,既可以验证某结论是正确的,也可以验证某结论是不正确的.
当堂检测
1.下列说法正确的是( )
D
A.经验、观察或实验完全可以判断一个数学结论的正确与否
B.推理是科学家的事,与我们没有多大的关系
C.对于自然数 , 一定是质数
D.有10个苹果,将它们放进9个筐中,则至少有一个筐中的苹果不少于2个
当堂检测
2.甲、乙、丙三个学生分别在A,B,C三所大学学习数学、物理、化学中的一个专业,若已知:①甲不在A校学习;②乙不在B校学习;③在B校学习的学数学;④在A校学习的不学化学;⑤乙不学物理,则 ( )
A.甲在B校学习,丙在A校学习
B.甲在B校学习,丙在C校学习
C.甲在C校学习,丙在B校学习
D.甲在C校学习,丙在A校学习
A
当堂检测
3.某公园计划砌一形状如图1所示的喷水池,后来有人建议改为图2的
形状,且外圆直径不变,喷水池边缘的高度、宽度不变,你认为砌喷水池的
边缘( )
图1
图2
C
A.图1需要的材料多 B.图2需要的材料多
C.图1、图2需要的材料一样多 D.无法确定
当堂检测
4.下列结论正确的是( )
A
A.400人至少有两人生日在同一天
B.300人至少有两人生日在同一天
C.300人一定没有两人生日在同一天
D.300人一定有两人生日在同一天
当堂检测
5.如图,大小相同的五角星按照一
定的规律进行排列,其中第一个图
形共有3个五角星,第二个图形共
30
有6个五角星,第三个图形共有9个五角星, ,则第十个图形五角星
的个数为____.
当堂检测
6.小鹿发现当 , ,0,1,2,3, 时,代数式 的值
均大于0,故小鹿断定: “对于任意实数 ,代数式 的值
均大于0”,你认为小鹿的说法正确吗 为什么
解:不正确.
,
所以当 时,代数式 ,
所以小鹿的说法是不正确的.
为什么要证明数学结论必须经过严格的论证实验验证举出反例推理证明论证方法
感谢收看
第七章平行线的证明
7.1为什么要证明
北师大版 数学 八年级 上册
学习目标
1.初步体会观察、猜测得到的结论不一定正确.
2.通过探索,初步了解数字中推理的重要性.
3.初步了解要判定一个数学结论正确与否,需要进行有根有据的推理.
情景导入
静态的没有循环帧的gif图片你看到的这些静止的图片是不是在动呢?据心理医生说,图片与心理承受力有关,你的心理承受力越强,图片运动越慢。美国曾经以此作为犯罪嫌疑人的心理测试,据说犯罪嫌疑人看到的图片是高速运动的。
情景导入
【解析】英国视觉科学家、艺术家尼古拉斯·韦德向我们展示了他的弗雷泽螺旋幻觉的变体形式。虽然图形看起来像螺旋,但实际上它是一系列同心圆。
韦德螺旋:
这真是一个螺旋吗?
探索新知
数学的结论必须经过严格的论证
一
平行线:不敢相信图中的横线是平行的,不过它们就是平行线.
想一想:仅靠观察得到的结论一定正确吗?
不一定正确.
图中的横线是平行的吗?
探索新知
活动一:图1中两条线段a、b的长度相等吗?图2中的四边形是正方形吗?请你先观察,再设法检验你观察到的结论.
图1
b
a
图2
观察未必可靠
测量可以帮助我们验证猜想
探索新知
例1:当n=1,2,3,4,5时,代数式n2-3n+7的值是质数吗?你能肯定:对于所有的自然数,式子n2-3n+7的值都是质数吗?
解:当n=1,2,3,4,5时,n2-3n+7的值分别是5,5,7,11,17,全是质数.而当n=6时,n2-3n+7=62-18+7=25=52.
所以对于所有自然数,式子n2-3n+7的值不都是质数.
探索新知
【解后思考】判断一个数学结论是否正确,仅仅依靠经验、观察是不够的,必须给出严格的证明或实验验证.如此题,我们可以把1,2,3,4,5,6等自然数代入n2-3n+7中进行验证.
总结归纳
探索新知
1.许多猜想的结论,数学上的一些结论以及数学之外的其他事实,应当追其缘由,推理证明是非常必要的.
(1)要判断一个数学结论是否正确,仅仅依靠实验,观察、归纳是不够的,必须进行有根有据的证明.
(2)没有经过严格的推理,仅由若干特例归纳得出的结论可能潜藏着错误.
(3)对一个结论要肯定其是正确的,必须通过一步一步推理,论证才能下结论.
探索新知
2.要点精析:
(1)直觉有时会产生错误,不是永远可信的;
(2)图形的性质并不都是通过测量得出的;
(3)对少数具体例子的观察、测量或计算得出的结论,并不能保证一般情况下都成立;
(4)只有通过推理的方法研究问题,才能揭示问题的本质.
总结归纳
探索新知
检验数学结论的常用方法
二
【类型一】 实验验证
例2:线段a与线段b比较谁更长?
a
b
解:视觉上看,我们感觉线段a比线段b长一点,但用直尺来测量两条线段的长度,我们发现线段a与线段b一样长.
a
探索新知
【类型二】 举出反例
例3:当n为正整数时,代数式(n2-5n+5)2的值都等于1吗?
【分析】对于代数式(n2-5n+5)2,n的取值为正整数,要判断(n2-5n+5)2的值是否为1,可以先取值分别求出代数式的值.
探索新知
解:当n=1时,(n2-5n+5)2=12=1;
当n=2时,(n2-5n+5)2=(-1)2=1;
当n=3时,(n2-5n+5)2=(-1)2=1;
当n=4时,(n2-5n+5)2=12=1;
当n=5时,(n2-5n+5)2=52=25≠1.
所以当n为正整数时,(n2-5n+5)2不一定等于1.
探索新知
【类型三】 推理论证
例4:如图,从点O出发作出四条射线OA、OB、OC、OD,已知OA⊥OC,OB⊥OD.若∠BOC=30°,∠AOB和∠COD有什么关系呢?
【分析】∠AOB、∠COD均与∠BOC互余,根据角的和、差关系,可求∠AOB与∠COD的度数.通过计算发现∠AOB=∠COD.
探索新知
解:因为OA⊥OC,OB⊥OD,
所以∠AOC=∠BOD=90°.
因为∠BOC=30°,
所以∠AOB=∠AOC-∠BOC=90°-30°=60°,
∠COD=∠BOD-∠BOC=90°-30°=60°,
所以∠AOB=∠COD.
探索新知
总结归纳
1.检验数学结论常用的方法:
主要有:实验验证、举出反例、推理证明.实验验证是最基本的方法,它直接反映由具体到抽象、由特殊到一般的逻辑思维方法;举出反例常用于说明该数学结论不一定成立;推理证明是最可靠、最科学的方法,是我们要掌握的重点.实际上每一个正确的结论都需要我们进行严格的推理证明才能得出.检验数学结论的具体过程:观察、度量、实验→猜想归纳→结论→推理正确结论.
探索新知
总结归纳
2.应用:检验数学结论常用的三种方法的应用:
实验验证法常用于检验一些比较直观、简单的结论;举出反例法多用于验证某结论是不是正确的;推理证明主要用来进行严格的推理论证,既可以验证某结论是正确的,也可以验证某结论是不正确的.
当堂检测
1.下列说法正确的是( )
D
A.经验、观察或实验完全可以判断一个数学结论的正确与否
B.推理是科学家的事,与我们没有多大的关系
C.对于自然数 , 一定是质数
D.有10个苹果,将它们放进9个筐中,则至少有一个筐中的苹果不少于2个
当堂检测
2.甲、乙、丙三个学生分别在A,B,C三所大学学习数学、物理、化学中的一个专业,若已知:①甲不在A校学习;②乙不在B校学习;③在B校学习的学数学;④在A校学习的不学化学;⑤乙不学物理,则 ( )
A.甲在B校学习,丙在A校学习
B.甲在B校学习,丙在C校学习
C.甲在C校学习,丙在B校学习
D.甲在C校学习,丙在A校学习
A
当堂检测
3.某公园计划砌一形状如图1所示的喷水池,后来有人建议改为图2的
形状,且外圆直径不变,喷水池边缘的高度、宽度不变,你认为砌喷水池的
边缘( )
图1
图2
C
A.图1需要的材料多 B.图2需要的材料多
C.图1、图2需要的材料一样多 D.无法确定
当堂检测
4.下列结论正确的是( )
A
A.400人至少有两人生日在同一天
B.300人至少有两人生日在同一天
C.300人一定没有两人生日在同一天
D.300人一定有两人生日在同一天
当堂检测
5.如图,大小相同的五角星按照一
定的规律进行排列,其中第一个图
形共有3个五角星,第二个图形共
30
有6个五角星,第三个图形共有9个五角星, ,则第十个图形五角星
的个数为____.
当堂检测
6.小鹿发现当 , ,0,1,2,3, 时,代数式 的值
均大于0,故小鹿断定: “对于任意实数 ,代数式 的值
均大于0”,你认为小鹿的说法正确吗 为什么
解:不正确.
,
所以当 时,代数式 ,
所以小鹿的说法是不正确的.
为什么要证明数学结论必须经过严格的论证实验验证举出反例推理证明论证方法
感谢收看
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
