期末综合复习试题 上学期初中数学人教版八年级上册
文档属性
| 名称 | 期末综合复习试题 上学期初中数学人教版八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 795.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-13 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末综合复习试题
2024--2025学年上学期初中数学人教版八年级上册
一、单选题
1.观察下面图标,其中可以抽象成轴对称图形的是( )
A. B. C. D.
2.下列四个式子中,计算正确的是( )
A. B. C. D.
3.已知多项式是一个完全平方式,则的值为( )
A.2 B.4 C.2或-2 D.4或-4
4.下列因式分解结果正确的是( )
A. B.
C. D.
5.如图所示,三点在同一条直线上,,,,则下列结论错误的是( )
A.与互余 B.
C. D.
6.若分式的值为0,则x的值为( )
A.0 B. C.0或 D.1
7.如图,点,在直线的同侧,,添加一个适当的条件后,仍不能使得成立的是( )
A. B. C. D.
8.我国古代数学家祖冲之推算出的近似值为,它与的误差小于0.0000003.将0.0000003用科学记数法可以表示为( )
A. B. C. D.
9.随着生活水平的提高,小林家购置了私家车,这样他乘坐私家车上学比乘坐公交车上学所需的时间少用了15分钟,现已知小林家距学校8千米,乘私家车平均速度是乘公交车平均速度的2.5倍,若设乘公交车平均每小时走x千米,根据题意可列方程为( )
A. B.
C. D.
10.下列等式从左到右的变形一定正确的是( )
A. B.
C. D.
11.若关于的方程的解为负数,则的取值范围是( )
A. B. C.且 D.且
12.如图,点D是∠FAB内的定点且AD=2,若点C、E分别是射线AF、AB上异于点A的动点,且△CDE周长的最小值是2时,∠FAB的度数是( )
A.30° B.45° C.60° D.90°
二、填空题
13.分解因式:x3﹣4x2﹣12x= .
14.关于x的分式方程-=0无解,则m= .
15.一个多边形的内角和是外角和的2倍,则这个多边形的边数为 .
16.如图,点B、A、D、E在同一直线上,∥,,要使,则只需添加一个适当的条件是 .(只填一个即可)
17.如图,的周长为,的垂直平分线交于点,为垂足,,则的周长为 .
18.已知,…,若 (a,b为正整数),则 , .
三、解答题
19.解分式方程:
(1);
(2).
20.因式分解:
(1);
(2);
(3);
(4).
21.已知,求下列式子的值:
(1);
(2).
22.已知关于x的分式方程的解为非负数,求k的取值范围.
23.甲、乙两个工程队均参与某筑路工程,先由甲队筑路公里,再由乙队完成剩下的筑路工程,已知乙队筑路总公里数是甲队筑路总公里数的倍,甲队比乙队多筑路天.
(1)求乙队筑路的总公里数;
(2)若甲、乙两队平均每天筑路公里数之比为,求乙队平均每天筑路多少公里.
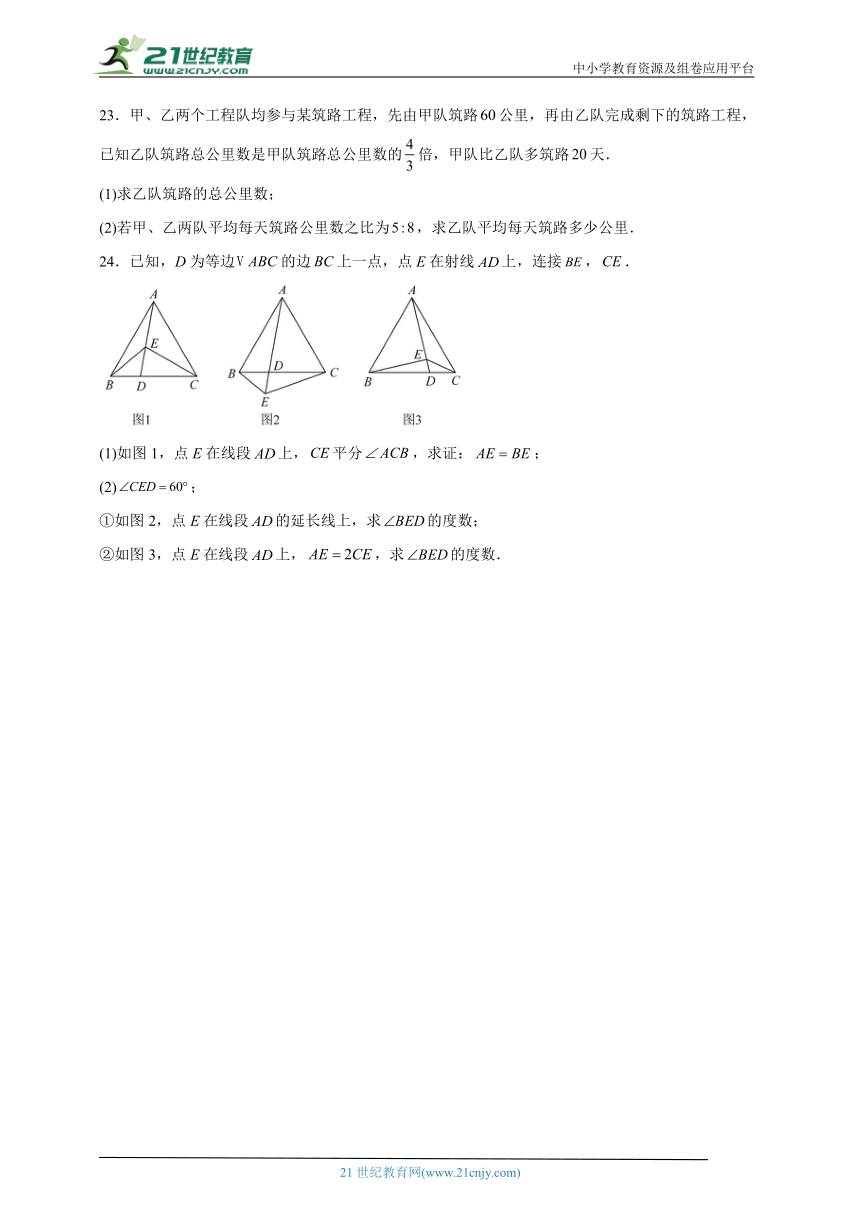
24.已知,D为等边的边上一点,点E在射线上,连接,.
(1)如图1,点E在线段上,平分,求证:;
(2);
①如图2,点E在线段的延长线上,求的度数;
②如图3,点E在线段上,,求的度数.
参考答案:
1.D
解:A、不可以抽象成轴对称图形,故本选项不符合题意;
B、不可以抽象成轴对称图形,故本选项不符合题意;
C、不可以抽象成轴对称图形,故本选项不符合题意;
D、可以抽象成轴对称图形,故本选项符合题意;
2.C
A.,A选项错误,所以A选项不符合题意;
B.,B选项错误,所以B选项不符合题意;
C.,C选项正确,所以C选项符合题意;
D.,D选项错误,所以D选项不符合题意.
3.C
解:∵=(x+|k|)2,
∴2|k|=4,
∴|k|=2,
可得k=-2或k=2,
4.D
解:A.,故A错误;
B.,故B错误;
C.,故C错误;
D.,故D正确.
5.D
解:∵,
∴,,
∵,
∴,
∴,故正确;
∴,故A正确;
在和中,,
∴,故C正确;
无法得出,故D错误;
6.A
解:∵分式的值为0,
∴,且
∴,
7.B
因为,共边,对选项一一分析,选择正确答案.
解:A.补充,可根据判定,故正确;
B.补充,不能判定,故错误;
C.补充,可根据判定,故正确;
D.补充,可根据判定,故正确.
8.A
解:0.0000003
9.D
设乘公交车平均每小时走x千米,根据题意列方程即可.
设乘公交车平均每小时走x千米,则乘私家车平均每小时走千米,
根据题意可列方程为.
10.B
此题这样考查了分式的基本性质,解题的关键是熟练掌握分式的基本性质.根据分式的基本性质,无论是把分式的分子和分母扩大还是缩小相同的倍数,都不要漏乘(除分子、分母中的任何一项,且扩大(缩小)的倍数不能为0,并且分式的值不变,由此即可判定选择项.
解:A、根据分式基本性质知道,故选项错误;
B、根据分式基本性质知道,故选项正确;
C、根据分式基本性质知道,故选项错误;
D、根据分式基本性质知道,故选项错误.
11.A
本题考查了分式方程解的情况,解题关键是熟练的解分式方程并根据题意列出不等式,注意:分式的分母不为.先解方程,再根据题意列不等式即可.
解:
关于的方程的解为负数,
,且,
解得:,
12.A
作D点分别关于AF、AB的对称点G、H,连接GH分别交AF、AB于C′、E′,利用轴对称的性质得AG=AD=AH=2,利用两点之间线段最短判断此时△CDE周长最小为DC′+DE′+C′E′=GH=2,可得△AGH是等边三角形,进而可得∠FAB的度数.
解:如图,作D点分别关于AF、AB的对称点G、H,连接GH分别交AF、AB于C′、E′,连接DC′,DE′,
此时△CDE周长最小为DC′+DE′+C′E′=GH=2,
根据轴对称的性质,得AG=AD=AH=2,∠DAF=∠GAF,∠DAB=∠HAB,
∴AG=AH=GH=2,
∴△AGH是等边三角形,
∴∠GAH=60°,
∴∠FAB=∠GAH=30°,
13.x(x+2)(x-6).
因式分解的步骤:先提公因式,再利用其它方法分解,注意分解要彻底.首先提取公因式x,然后利用十字相乘法求解,
解:x3﹣4x2﹣12x=x(x2﹣4x﹣12)=x(x+2)(x﹣6).
14.0或-4
解:方程去分母得:m-(x-2)=0,
解得:x=2+m,
∴当x=2时分母为0,方程无解,
即2+m=2,
∴m=0时方程无解.
当x=-2时分母为0,方程无解,
即2+m=-2,
∴m=-4时方程无解.
综上所述,m的值是0或-4.
故答案为:0或-4.
15.6
解:设这个多边形的边数为,
多边形的内角和是外角和的2倍,
,解得,
故答案为:.
16.(或)
解:若添加,
∵,
∴,
∵,
∴,即,
在和中,
,
∴;
若添加,
∵,
∴,
∵,
∴,即,
在和中,
,
∴,
若添加,
∵,
∴,
∵,
∴,即,
在和中,
,
∴.
故答案为:或或.
17..
解:∵的垂直平分线交于点,为垂足,
∴,,
∵的周长为,
∴,
∴,
∴的周长
故答案为.
18. 10 99
解:根据题意可得等号左边的整数和等号左边分数的分子是相同的,分母为分子的平方减1,
∵
∴.
故答案为:10,99.
19.(1)
(2)原分式方程无解
(1)解:方程两边乘,得:,
解得:,
检验:当时,,
所以原分式方程的解为;
(2)解:方程两边乘,得,
解得:,
检验:当时,,
所以原分式方程无解.
20.(1);
(2);
(3);
(4).
(1)解:
;
(2)解:
;
(3)解:
;
(4)解:
.
21.(1)
(2)3
(1)∵,
∴,
∴,
解得:;
(2)∵,
∴,
解得:,
∴.
22.且.
先解分式方程,再建立不等式求解即可.
解:解分式方程,得,
根据题意,得:且,
解得:且.
23.(1)乙队筑路的总千米数为80千米;
(2)乙队平均每天筑路千米.
(1)解:(千米),
∴乙队筑路的总千米数为80千米;
(2)解:设甲队平均每天筑路千米,则乙队平均每天筑路千米,
根据题意,得,
解得,
经检验,是原分式方程的解且符合题意,
,
答:乙队平均每天筑路千米.
24.(1)见解析
(2)①;②
(1)结合等边三角形的性质证明,即可作答;
(2)①延长至点F,使,证明,即可作答;②延长交于K,在的延长线上取一点M,使得,连接,,在上截取,使得,连接.先证明是等边三角形,再证明,可得,,即有,可得,再证明是等边三角形,可得,进而可得,即可得,再根据,即可作答.
(1)证明:如图1中,
∵是等边三角形,
∴,
∵平分,
∴,
∵,
∴,
∴.
(2)①解:如图2中,延长至点F,使,
∵是等边三角形,
∴,,
∵,
∴为等边三角形,
∴,,
∵,,
∴,
∵,,
∴,
∴;
②解:如图3中,延长交于K,在的延长线上取一点M,使得,连接,,在上截取,使得,连接.
∵是等边三角形,
∴,,
∵,,
∴是等边三角形,
∴,,
∴,
∴,
∴,,
∴,
∴,
∴,
∵,
∴是等边三角形,
∴,
∵,,
∴,
∵,
∴,
∴,,
∵,,
∴,
∴,
∵,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末综合复习试题
2024--2025学年上学期初中数学人教版八年级上册
一、单选题
1.观察下面图标,其中可以抽象成轴对称图形的是( )
A. B. C. D.
2.下列四个式子中,计算正确的是( )
A. B. C. D.
3.已知多项式是一个完全平方式,则的值为( )
A.2 B.4 C.2或-2 D.4或-4
4.下列因式分解结果正确的是( )
A. B.
C. D.
5.如图所示,三点在同一条直线上,,,,则下列结论错误的是( )
A.与互余 B.
C. D.
6.若分式的值为0,则x的值为( )
A.0 B. C.0或 D.1
7.如图,点,在直线的同侧,,添加一个适当的条件后,仍不能使得成立的是( )
A. B. C. D.
8.我国古代数学家祖冲之推算出的近似值为,它与的误差小于0.0000003.将0.0000003用科学记数法可以表示为( )
A. B. C. D.
9.随着生活水平的提高,小林家购置了私家车,这样他乘坐私家车上学比乘坐公交车上学所需的时间少用了15分钟,现已知小林家距学校8千米,乘私家车平均速度是乘公交车平均速度的2.5倍,若设乘公交车平均每小时走x千米,根据题意可列方程为( )
A. B.
C. D.
10.下列等式从左到右的变形一定正确的是( )
A. B.
C. D.
11.若关于的方程的解为负数,则的取值范围是( )
A. B. C.且 D.且
12.如图,点D是∠FAB内的定点且AD=2,若点C、E分别是射线AF、AB上异于点A的动点,且△CDE周长的最小值是2时,∠FAB的度数是( )
A.30° B.45° C.60° D.90°
二、填空题
13.分解因式:x3﹣4x2﹣12x= .
14.关于x的分式方程-=0无解,则m= .
15.一个多边形的内角和是外角和的2倍,则这个多边形的边数为 .
16.如图,点B、A、D、E在同一直线上,∥,,要使,则只需添加一个适当的条件是 .(只填一个即可)
17.如图,的周长为,的垂直平分线交于点,为垂足,,则的周长为 .
18.已知,…,若 (a,b为正整数),则 , .
三、解答题
19.解分式方程:
(1);
(2).
20.因式分解:
(1);
(2);
(3);
(4).
21.已知,求下列式子的值:
(1);
(2).
22.已知关于x的分式方程的解为非负数,求k的取值范围.
23.甲、乙两个工程队均参与某筑路工程,先由甲队筑路公里,再由乙队完成剩下的筑路工程,已知乙队筑路总公里数是甲队筑路总公里数的倍,甲队比乙队多筑路天.
(1)求乙队筑路的总公里数;
(2)若甲、乙两队平均每天筑路公里数之比为,求乙队平均每天筑路多少公里.
24.已知,D为等边的边上一点,点E在射线上,连接,.
(1)如图1,点E在线段上,平分,求证:;
(2);
①如图2,点E在线段的延长线上,求的度数;
②如图3,点E在线段上,,求的度数.
参考答案:
1.D
解:A、不可以抽象成轴对称图形,故本选项不符合题意;
B、不可以抽象成轴对称图形,故本选项不符合题意;
C、不可以抽象成轴对称图形,故本选项不符合题意;
D、可以抽象成轴对称图形,故本选项符合题意;
2.C
A.,A选项错误,所以A选项不符合题意;
B.,B选项错误,所以B选项不符合题意;
C.,C选项正确,所以C选项符合题意;
D.,D选项错误,所以D选项不符合题意.
3.C
解:∵=(x+|k|)2,
∴2|k|=4,
∴|k|=2,
可得k=-2或k=2,
4.D
解:A.,故A错误;
B.,故B错误;
C.,故C错误;
D.,故D正确.
5.D
解:∵,
∴,,
∵,
∴,
∴,故正确;
∴,故A正确;
在和中,,
∴,故C正确;
无法得出,故D错误;
6.A
解:∵分式的值为0,
∴,且
∴,
7.B
因为,共边,对选项一一分析,选择正确答案.
解:A.补充,可根据判定,故正确;
B.补充,不能判定,故错误;
C.补充,可根据判定,故正确;
D.补充,可根据判定,故正确.
8.A
解:0.0000003
9.D
设乘公交车平均每小时走x千米,根据题意列方程即可.
设乘公交车平均每小时走x千米,则乘私家车平均每小时走千米,
根据题意可列方程为.
10.B
此题这样考查了分式的基本性质,解题的关键是熟练掌握分式的基本性质.根据分式的基本性质,无论是把分式的分子和分母扩大还是缩小相同的倍数,都不要漏乘(除分子、分母中的任何一项,且扩大(缩小)的倍数不能为0,并且分式的值不变,由此即可判定选择项.
解:A、根据分式基本性质知道,故选项错误;
B、根据分式基本性质知道,故选项正确;
C、根据分式基本性质知道,故选项错误;
D、根据分式基本性质知道,故选项错误.
11.A
本题考查了分式方程解的情况,解题关键是熟练的解分式方程并根据题意列出不等式,注意:分式的分母不为.先解方程,再根据题意列不等式即可.
解:
关于的方程的解为负数,
,且,
解得:,
12.A
作D点分别关于AF、AB的对称点G、H,连接GH分别交AF、AB于C′、E′,利用轴对称的性质得AG=AD=AH=2,利用两点之间线段最短判断此时△CDE周长最小为DC′+DE′+C′E′=GH=2,可得△AGH是等边三角形,进而可得∠FAB的度数.
解:如图,作D点分别关于AF、AB的对称点G、H,连接GH分别交AF、AB于C′、E′,连接DC′,DE′,
此时△CDE周长最小为DC′+DE′+C′E′=GH=2,
根据轴对称的性质,得AG=AD=AH=2,∠DAF=∠GAF,∠DAB=∠HAB,
∴AG=AH=GH=2,
∴△AGH是等边三角形,
∴∠GAH=60°,
∴∠FAB=∠GAH=30°,
13.x(x+2)(x-6).
因式分解的步骤:先提公因式,再利用其它方法分解,注意分解要彻底.首先提取公因式x,然后利用十字相乘法求解,
解:x3﹣4x2﹣12x=x(x2﹣4x﹣12)=x(x+2)(x﹣6).
14.0或-4
解:方程去分母得:m-(x-2)=0,
解得:x=2+m,
∴当x=2时分母为0,方程无解,
即2+m=2,
∴m=0时方程无解.
当x=-2时分母为0,方程无解,
即2+m=-2,
∴m=-4时方程无解.
综上所述,m的值是0或-4.
故答案为:0或-4.
15.6
解:设这个多边形的边数为,
多边形的内角和是外角和的2倍,
,解得,
故答案为:.
16.(或)
解:若添加,
∵,
∴,
∵,
∴,即,
在和中,
,
∴;
若添加,
∵,
∴,
∵,
∴,即,
在和中,
,
∴,
若添加,
∵,
∴,
∵,
∴,即,
在和中,
,
∴.
故答案为:或或.
17..
解:∵的垂直平分线交于点,为垂足,
∴,,
∵的周长为,
∴,
∴,
∴的周长
故答案为.
18. 10 99
解:根据题意可得等号左边的整数和等号左边分数的分子是相同的,分母为分子的平方减1,
∵
∴.
故答案为:10,99.
19.(1)
(2)原分式方程无解
(1)解:方程两边乘,得:,
解得:,
检验:当时,,
所以原分式方程的解为;
(2)解:方程两边乘,得,
解得:,
检验:当时,,
所以原分式方程无解.
20.(1);
(2);
(3);
(4).
(1)解:
;
(2)解:
;
(3)解:
;
(4)解:
.
21.(1)
(2)3
(1)∵,
∴,
∴,
解得:;
(2)∵,
∴,
解得:,
∴.
22.且.
先解分式方程,再建立不等式求解即可.
解:解分式方程,得,
根据题意,得:且,
解得:且.
23.(1)乙队筑路的总千米数为80千米;
(2)乙队平均每天筑路千米.
(1)解:(千米),
∴乙队筑路的总千米数为80千米;
(2)解:设甲队平均每天筑路千米,则乙队平均每天筑路千米,
根据题意,得,
解得,
经检验,是原分式方程的解且符合题意,
,
答:乙队平均每天筑路千米.
24.(1)见解析
(2)①;②
(1)结合等边三角形的性质证明,即可作答;
(2)①延长至点F,使,证明,即可作答;②延长交于K,在的延长线上取一点M,使得,连接,,在上截取,使得,连接.先证明是等边三角形,再证明,可得,,即有,可得,再证明是等边三角形,可得,进而可得,即可得,再根据,即可作答.
(1)证明:如图1中,
∵是等边三角形,
∴,
∵平分,
∴,
∵,
∴,
∴.
(2)①解:如图2中,延长至点F,使,
∵是等边三角形,
∴,,
∵,
∴为等边三角形,
∴,,
∵,,
∴,
∵,,
∴,
∴;
②解:如图3中,延长交于K,在的延长线上取一点M,使得,连接,,在上截取,使得,连接.
∵是等边三角形,
∴,,
∵,,
∴是等边三角形,
∴,,
∴,
∴,
∴,,
∴,
∴,
∴,
∵,
∴是等边三角形,
∴,
∵,,
∴,
∵,
∴,
∴,,
∵,,
∴,
∴,
∵,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
