2024-2025学年北师大版数学九年级上册期末培优训练(含答案)
文档属性
| 名称 | 2024-2025学年北师大版数学九年级上册期末培优训练(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 369.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-15 00:00:00 | ||
图片预览




文档简介
2024-2025学年北师大版数学九年级上册期末培优训练
一、单选题(共10题;共30分)
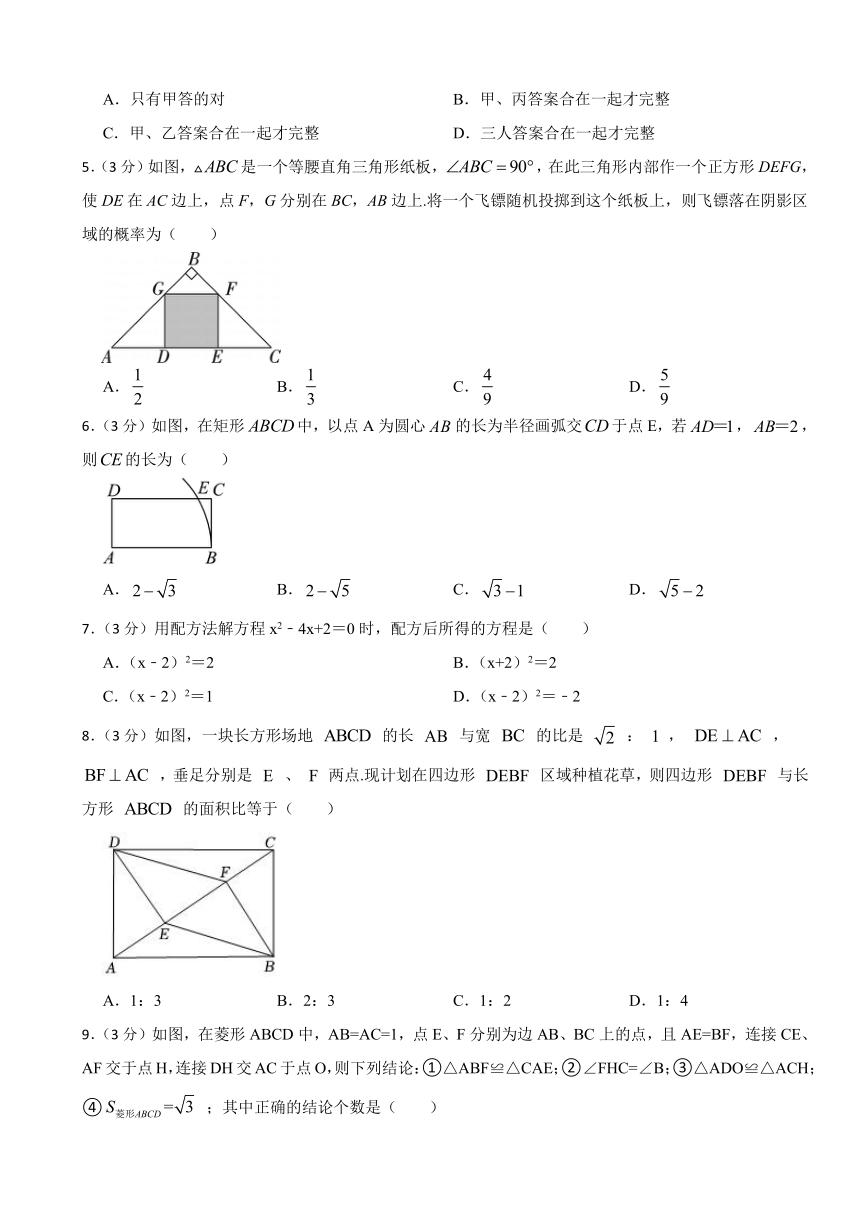
1.(3分)如图,在矩形中,、相交于点O,平分交于点E,若,则的度数为( )
A. B. C. D.
2.(3分)关于x的一元二次方程有两个不相等的实数根,则a的取值范围是( )
A. B. C. D.且
3.(3分)如图,已知和是以点为位似中心的位似图形,点在线叹上.周长为4,若,财的周长为( )
A.12 B.10 C.8 D.6
4.(3分)七巧板是一种开发智力的玩具,为提高学生的感知能力,老师投影演示如下:在正方形纸板中,为对角线,,分别为,的中点,分别交,于,两点,,分别为,的中点,连接,,沿图中实线剪开即可得到一副七巧板.通过观察演示过程,
甲同学得出:图中的三角形都是等腰直角三角形;
乙同学得出:四边形是菱形;
丙同学得出:四边形的面积占正方形面积的.
则正确的是( )
A.只有甲答的对 B.甲、丙答案合在一起才完整
C.甲、乙答案合在一起才完整 D.三人答案合在一起才完整
5.(3分)如图,是一个等腰直角三角形纸板,,在此三角形内部作一个正方形DEFG,使DE在AC边上,点F,G分别在BC,AB边上.将一个飞镖随机投掷到这个纸板上,则飞镖落在阴影区域的概率为( )
A. B. C. D.
6.(3分)如图,在矩形中,以点A为圆心的长为半径画弧交于点E,若,,则的长为( )
A. B. C. D.
7.(3分)用配方法解方程x2﹣4x+2=0时,配方后所得的方程是( )
A.(x﹣2)2=2 B.(x+2)2=2
C.(x﹣2)2=1 D.(x﹣2)2=﹣2
8.(3分)如图,一块长方形场地 的长 与宽 的比是 : , , ,垂足分别是 、 两点.现计划在四边形 区域种植花草,则四边形 与长方形 的面积比等于( )
A.1:3 B.2:3 C.1:2 D.1:4
9.(3分)如图,在菱形ABCD中,AB=AC=1,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AC于点O,则下列结论:①△ABF≌△CAE;②∠FHC=∠B;③△ADO≌△ACH;④ ;其中正确的结论个数是( )
A.1个 B.2个 C.3个 D.4个
10.(3分)如图,已知四边形为正方形,为对角线上一点,连接,过点作,交的延长线于点,以,为邻边作矩形,连接.下列结论:①矩形是正方形;②;③;④.下列正确的选项是( )
A.①②④ B.①③ C.①②③ D.②③④
二、填空题(共6题;共18分)
11.(3分)《算法统宗》记载古人丈量田地的诗:“昨日丈量地回,记得长步整三十.广斜相并五十步,不知几亩及分厘.”其大意是:昨天丈量了田地回到家,记得长方形田的长为30步,宽和对角线之和为50步.不知该田的面积有多少?请帮他算一算,该田的面积为 平方步.
12.(3分)用配方法解一元二次方程,则方程可变形为 .
13.(3分)在实数范围内,对于任意实数,规定一种新运算:.例如:.若,则 .
14.(3分)如图所示,某校数学兴趣小组利用标杆测量建筑物的高度,已知标杆高m,测得m,m.则建筑物的高是 m.
15.(3分)已知关于的方程.若等腰三角形的一边长,另两边长,恰好是这个方程的两个根,求此三角形的周长 .
16.(3分)在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.5m,木竿PQ的影子有一部分落在了墙上,它的影子QN=1.8m,MN=0.8m,木竿PQ的长度为 .
三、解答题(共7题;共52分)
17.(6分)解方程:
(1)(3分)
(2)(3分)
18.(7分)为传承中华优秀传统文化,深入挖掘中华经典诗词中所蕴含的民族正气、爱国情怀、道德品质和艺术魅力,引领诗词教育发展,我校举办诗词大赛,第一轮为经典诵读参赛者从《短歌行》《将进酒》《观沧海》《木兰辞》(分别用A、B、C、D表示)中随机抽取一首进行朗诵:第二轮为诗词讲解,参赛者从《蒹葭》《沁园春·雪》《念奴娇·赤壁怀古》(分别用E、F、G表示)中随机抽取一首进行讲解,小明和晓慧都参加了诗词大赛.
(1)(3分)小明第一轮抽到《将进酒》的概率是______.
(2)(4分)利用树状图或列表法,求晓慧第一轮抽中《木兰辞》且第二轮抽中《沁园春·雪》的概率.
19.(7分)已知一元二次方程
(1)(3分) 若该一元二次方程有两个实数根,求m的范围.
(2)(4分) 若该一元二次方程有一个根为1,求方程的另一个实数根.
20.(7分)随着疫情形势稳定向好,“复工复产”成为主旋律.某生产无人机公司统计发现,公司今年2月份生产A型无人机2000架,4月份生产A型无人机达到12500架.
(1)(3分)求该公司生产A型无人机每月产量的平均增长率;
(2)(4分)该公司还生产B型无人机,已知生产1架A型无人机的成本是200元,生产1架B型无人机的成本是300元,现要生产A、B两种型号的无人机共100架,其中A型无人机的数量不超过B型无人机数量的3倍,公司生产A、B两种型号的无人机各多少架时才可能使生产成本最少?
21.(8分)已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA中点,点P在BC上以每秒1个单位的速度由C向B运动,设运动时间为t秒.
(1)△ODP的面积S=________.
(2)t为何值时,四边形PODB是平行四边形?
(3)在线段PB上是否存在一点Q,使得ODQP为菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由;
(4)若△OPD为等腰三角形,请写出所有满足条件的点P的坐标(请直接写出答案,不必写过程)
22.(8分)如图,菱形的边长为,,对角线、相交于点,点在对角线上,连接,作,且边与直线相交于点.
(1)(4分)求菱形的面积;
(2)(4分)求证:
23.(9分)模拟经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种情况是等可能的,当同向行驶的三辆汽车经过这个十字路口时,
(1)(3分)求三辆车全部同向而行的概率.
(2)(3分)求至少有两辆车向左转的概率.
(3)(3分)这个路口汽车左转.右转、直行的指示绿灯交替亮起,亮的时间均为30秒.交管部门对这个十字路口交通高峰时段车流量作了统计,发现汽车在此十字路口向右转的频率为,向左转和直行的频率均为,在绿灯亮的总时间不变的条件下,为使交通更加通畅,请你用统计的知识对此十字路口三个方向的绿灯亮的时间做出合理的调整.
答案解析部分
1.B
2.D
3.A
4.B
5.C
6.A
7.A
8.A
9.B
10.B
11.480
12.
13.0或-2
14.20
15.16或22
16.3.2m
17.(1),
(2)
18.(1)
(2)
19.(1)解:∵该一元二次方程有两个实数根
∴
∴
(2)解:把
得:
∴
20.(1)解:设该公司生产A型无人机每月产量的平均增长率为x,根据题意可得:
2000(1+x)2=12500,
解得:x1=1.5=150%,x2=﹣3.5(不合题意舍去),
答:该公司生产A型无人机每月产量的平均增长率为150%;
(2)解:设生产A型号无人机a架,则生产B型号无人机(100﹣a)架,需要成本为w元,依据题意可得:
a≤3(100﹣a),
解得:a≤75,
w=200a+300(100﹣a)=﹣100a+30000,
∵﹣100<0,
∴当a的值增大时,w的值减小,
∵a为整数,
∴当a=75时,w取最小值,此时100﹣75=25,
w=﹣100×75+30000=22500,
∴公司生产A型号无人机75架,生产B型号无人机25架成本最小.
21.(1)10;(2)5;(3)(8,4);(4)满足条件的点P的坐标为P1(3,4),P2(2.5,4),P3(2,4),P4(8,4).
22.(1)解:四边形是菱形,
,,,
,
是等边三角形,
,,
,
菱形的面积;
(2)证明:连接,
垂直平分,
,
,
,
,
,
,
,,
,
,
,
,
.
23.(1)解:分别用A、B、C表示向左转,直行,向右转,根据题意画出树状图如下:
由图可知:共有27种等可能的结果数,三辆车全部同向而行的有3种情况,
∴P( 三辆车全部同向而行的概率)= ;
(2)解:∵至少有两辆车向左转的情况数有7种,
∴P( 至少有两辆车向左转 )=;
(3)解:∵汽车向右转、向左转,直行的概率分别为,
∴ 在绿灯亮的总时间不变的条件下可以调整绿灯亮的时间如下:
向左转及直行的绿灯亮的时间都为:(秒),
向右转绿灯亮的时间为:(秒).
一、单选题(共10题;共30分)
1.(3分)如图,在矩形中,、相交于点O,平分交于点E,若,则的度数为( )
A. B. C. D.
2.(3分)关于x的一元二次方程有两个不相等的实数根,则a的取值范围是( )
A. B. C. D.且
3.(3分)如图,已知和是以点为位似中心的位似图形,点在线叹上.周长为4,若,财的周长为( )
A.12 B.10 C.8 D.6
4.(3分)七巧板是一种开发智力的玩具,为提高学生的感知能力,老师投影演示如下:在正方形纸板中,为对角线,,分别为,的中点,分别交,于,两点,,分别为,的中点,连接,,沿图中实线剪开即可得到一副七巧板.通过观察演示过程,
甲同学得出:图中的三角形都是等腰直角三角形;
乙同学得出:四边形是菱形;
丙同学得出:四边形的面积占正方形面积的.
则正确的是( )
A.只有甲答的对 B.甲、丙答案合在一起才完整
C.甲、乙答案合在一起才完整 D.三人答案合在一起才完整
5.(3分)如图,是一个等腰直角三角形纸板,,在此三角形内部作一个正方形DEFG,使DE在AC边上,点F,G分别在BC,AB边上.将一个飞镖随机投掷到这个纸板上,则飞镖落在阴影区域的概率为( )
A. B. C. D.
6.(3分)如图,在矩形中,以点A为圆心的长为半径画弧交于点E,若,,则的长为( )
A. B. C. D.
7.(3分)用配方法解方程x2﹣4x+2=0时,配方后所得的方程是( )
A.(x﹣2)2=2 B.(x+2)2=2
C.(x﹣2)2=1 D.(x﹣2)2=﹣2
8.(3分)如图,一块长方形场地 的长 与宽 的比是 : , , ,垂足分别是 、 两点.现计划在四边形 区域种植花草,则四边形 与长方形 的面积比等于( )
A.1:3 B.2:3 C.1:2 D.1:4
9.(3分)如图,在菱形ABCD中,AB=AC=1,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AC于点O,则下列结论:①△ABF≌△CAE;②∠FHC=∠B;③△ADO≌△ACH;④ ;其中正确的结论个数是( )
A.1个 B.2个 C.3个 D.4个
10.(3分)如图,已知四边形为正方形,为对角线上一点,连接,过点作,交的延长线于点,以,为邻边作矩形,连接.下列结论:①矩形是正方形;②;③;④.下列正确的选项是( )
A.①②④ B.①③ C.①②③ D.②③④
二、填空题(共6题;共18分)
11.(3分)《算法统宗》记载古人丈量田地的诗:“昨日丈量地回,记得长步整三十.广斜相并五十步,不知几亩及分厘.”其大意是:昨天丈量了田地回到家,记得长方形田的长为30步,宽和对角线之和为50步.不知该田的面积有多少?请帮他算一算,该田的面积为 平方步.
12.(3分)用配方法解一元二次方程,则方程可变形为 .
13.(3分)在实数范围内,对于任意实数,规定一种新运算:.例如:.若,则 .
14.(3分)如图所示,某校数学兴趣小组利用标杆测量建筑物的高度,已知标杆高m,测得m,m.则建筑物的高是 m.
15.(3分)已知关于的方程.若等腰三角形的一边长,另两边长,恰好是这个方程的两个根,求此三角形的周长 .
16.(3分)在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.5m,木竿PQ的影子有一部分落在了墙上,它的影子QN=1.8m,MN=0.8m,木竿PQ的长度为 .
三、解答题(共7题;共52分)
17.(6分)解方程:
(1)(3分)
(2)(3分)
18.(7分)为传承中华优秀传统文化,深入挖掘中华经典诗词中所蕴含的民族正气、爱国情怀、道德品质和艺术魅力,引领诗词教育发展,我校举办诗词大赛,第一轮为经典诵读参赛者从《短歌行》《将进酒》《观沧海》《木兰辞》(分别用A、B、C、D表示)中随机抽取一首进行朗诵:第二轮为诗词讲解,参赛者从《蒹葭》《沁园春·雪》《念奴娇·赤壁怀古》(分别用E、F、G表示)中随机抽取一首进行讲解,小明和晓慧都参加了诗词大赛.
(1)(3分)小明第一轮抽到《将进酒》的概率是______.
(2)(4分)利用树状图或列表法,求晓慧第一轮抽中《木兰辞》且第二轮抽中《沁园春·雪》的概率.
19.(7分)已知一元二次方程
(1)(3分) 若该一元二次方程有两个实数根,求m的范围.
(2)(4分) 若该一元二次方程有一个根为1,求方程的另一个实数根.
20.(7分)随着疫情形势稳定向好,“复工复产”成为主旋律.某生产无人机公司统计发现,公司今年2月份生产A型无人机2000架,4月份生产A型无人机达到12500架.
(1)(3分)求该公司生产A型无人机每月产量的平均增长率;
(2)(4分)该公司还生产B型无人机,已知生产1架A型无人机的成本是200元,生产1架B型无人机的成本是300元,现要生产A、B两种型号的无人机共100架,其中A型无人机的数量不超过B型无人机数量的3倍,公司生产A、B两种型号的无人机各多少架时才可能使生产成本最少?
21.(8分)已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA中点,点P在BC上以每秒1个单位的速度由C向B运动,设运动时间为t秒.
(1)△ODP的面积S=________.
(2)t为何值时,四边形PODB是平行四边形?
(3)在线段PB上是否存在一点Q,使得ODQP为菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由;
(4)若△OPD为等腰三角形,请写出所有满足条件的点P的坐标(请直接写出答案,不必写过程)
22.(8分)如图,菱形的边长为,,对角线、相交于点,点在对角线上,连接,作,且边与直线相交于点.
(1)(4分)求菱形的面积;
(2)(4分)求证:
23.(9分)模拟经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种情况是等可能的,当同向行驶的三辆汽车经过这个十字路口时,
(1)(3分)求三辆车全部同向而行的概率.
(2)(3分)求至少有两辆车向左转的概率.
(3)(3分)这个路口汽车左转.右转、直行的指示绿灯交替亮起,亮的时间均为30秒.交管部门对这个十字路口交通高峰时段车流量作了统计,发现汽车在此十字路口向右转的频率为,向左转和直行的频率均为,在绿灯亮的总时间不变的条件下,为使交通更加通畅,请你用统计的知识对此十字路口三个方向的绿灯亮的时间做出合理的调整.
答案解析部分
1.B
2.D
3.A
4.B
5.C
6.A
7.A
8.A
9.B
10.B
11.480
12.
13.0或-2
14.20
15.16或22
16.3.2m
17.(1),
(2)
18.(1)
(2)
19.(1)解:∵该一元二次方程有两个实数根
∴
∴
(2)解:把
得:
∴
20.(1)解:设该公司生产A型无人机每月产量的平均增长率为x,根据题意可得:
2000(1+x)2=12500,
解得:x1=1.5=150%,x2=﹣3.5(不合题意舍去),
答:该公司生产A型无人机每月产量的平均增长率为150%;
(2)解:设生产A型号无人机a架,则生产B型号无人机(100﹣a)架,需要成本为w元,依据题意可得:
a≤3(100﹣a),
解得:a≤75,
w=200a+300(100﹣a)=﹣100a+30000,
∵﹣100<0,
∴当a的值增大时,w的值减小,
∵a为整数,
∴当a=75时,w取最小值,此时100﹣75=25,
w=﹣100×75+30000=22500,
∴公司生产A型号无人机75架,生产B型号无人机25架成本最小.
21.(1)10;(2)5;(3)(8,4);(4)满足条件的点P的坐标为P1(3,4),P2(2.5,4),P3(2,4),P4(8,4).
22.(1)解:四边形是菱形,
,,,
,
是等边三角形,
,,
,
菱形的面积;
(2)证明:连接,
垂直平分,
,
,
,
,
,
,
,,
,
,
,
,
.
23.(1)解:分别用A、B、C表示向左转,直行,向右转,根据题意画出树状图如下:
由图可知:共有27种等可能的结果数,三辆车全部同向而行的有3种情况,
∴P( 三辆车全部同向而行的概率)= ;
(2)解:∵至少有两辆车向左转的情况数有7种,
∴P( 至少有两辆车向左转 )=;
(3)解:∵汽车向右转、向左转,直行的概率分别为,
∴ 在绿灯亮的总时间不变的条件下可以调整绿灯亮的时间如下:
向左转及直行的绿灯亮的时间都为:(秒),
向右转绿灯亮的时间为:(秒).
同课章节目录
