24.1.4圆周角(三)习题课
文档属性
| 名称 | 24.1.4圆周角(三)习题课 |

|
|
| 格式 | rar | ||
| 文件大小 | 111.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-11-10 00:00:00 | ||
图片预览





文档简介
课件24张PPT。 2、在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.1、顶点在圆上,两边与圆相交的角,叫圆周角.推论:半圆或直径所对的圆周角都相等,都等于
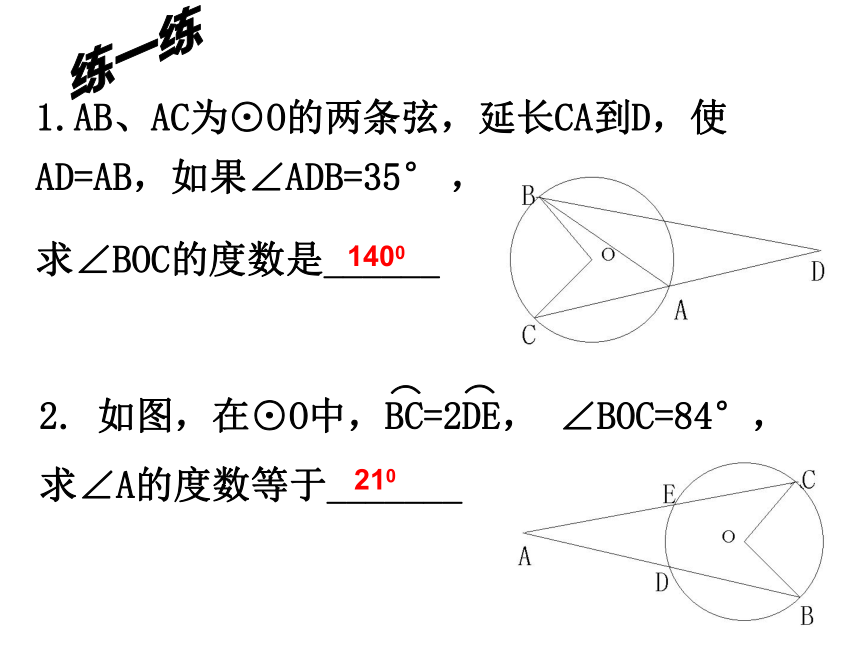
90°; 90°的圆周角所对的弦是圆的直径.3、圆的内接四边形对角互补。复习与巩固1.AB、AC为⊙O的两条弦,延长CA到D,使 AD=AB,如果∠ADB=35° ,
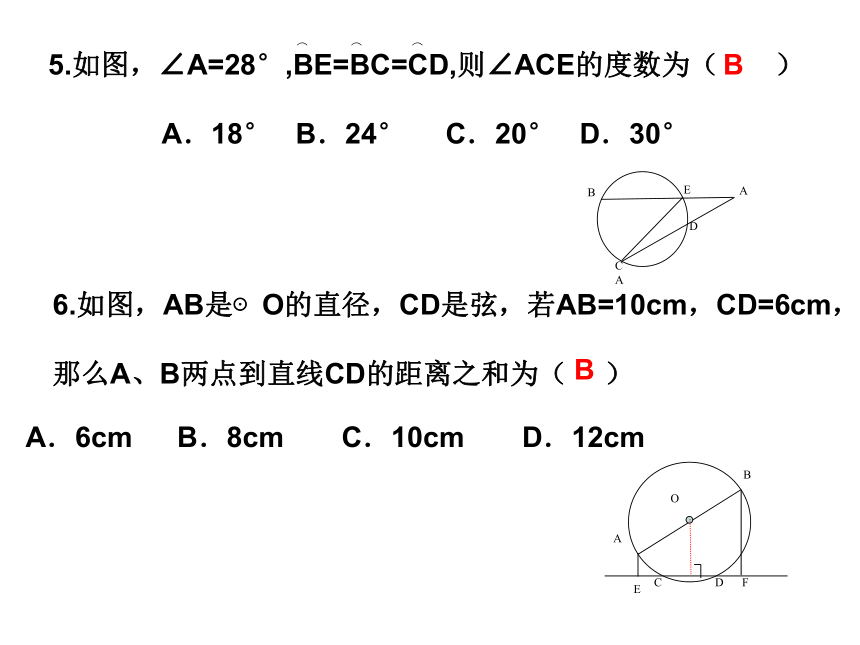
求∠BOC的度数是______1400210练一练3.如图,圆心角∠AOB=100°,则∠ACB=______。13006605.如图,∠A=28°,BE=BC=CD,则∠ACE的度数为( )
A.18° B.24° C.20° D.30°6.如图,AB是⊙O的直径,CD是弦,若AB=10cm,CD=6cm,
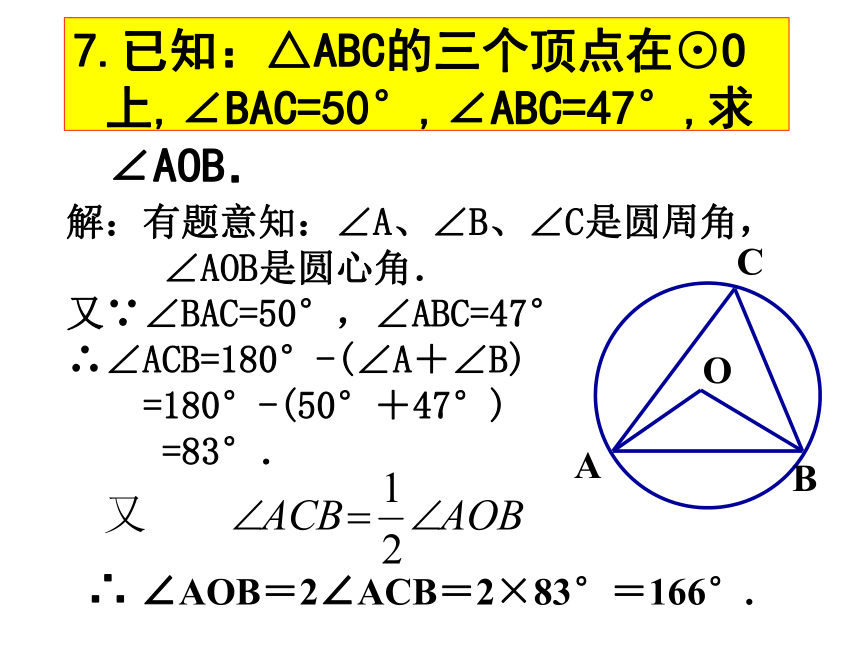
那么A、B两点到直线CD的距离之和为( )FDEABOCA.6cm B.8cm C.10cm D.12cmBB⌒⌒⌒7.已知:△ABC的三个顶点在⊙O上,∠BAC=50°,∠ABC=47°,求∠AOB.解:有题意知:∠A、∠B、∠C是圆周角,
∠AOB是圆心角.
又∵∠BAC=50°,∠ABC=47° ∴∠ACB=180°-(∠A+∠B)
=180°-(50°+47°)
=83°.∴ ∠AOB=2∠ACB=2×83°=166°.2009.11.6例1如图,P是△ABC的外接圆上的一点∠APC=∠CPB=60°。求证:△ABC是等边三角形证明:∵∠ABC和∠APC
都是⌒所对的圆周角。 AC∴∠ABC=∠APC=60°(同弧所对的圆周角相等)同理,∵∠BAC和∠CPB都是⌒所对的圆周角,BC∴∠BAC=∠CPB=60°。∴△ABC等边三角形。例2.如图OA、OB、OC都是⊙O的半径,∠AOB=2∠BOC.
求证:∠ACB=∠BAC.例3.求证:如果一个三角形一边上的中线等于这条边的一半,那么这个三角形是直角三角形。求证:△ABC是直角三角形。 已知:△ABC中,CD是AB边上的中线,CD= AB,CD是AB边上的中线
∵AD=BD 右∵AD=CD
∴∠A=∠ACD ∵BD=DC ∴∠DCB=∠B ∵∠A+∠ACD+∠DCB+∠B=180° 2∠ACD+2∠DAC=180° ∴∠BAD+∠DCB=90° ∴∠ACB=900
即三角形是直角三角形 例4.如图:AB是⊙O的直径,弦CD⊥AB于点E,G是⌒上任意一点,延长AG,与DC的延长线相交于点F,连接AD,GD,CG,找出图中所有和∠ADC相等的角,并说明理由.ACABDGFCEO1.如图7-59,AB是⊙O的直径,AB=2cm,
点C在圆周上,且∠BAC=30°,∠ABD=120°,
CD⊥BD于D.求BD的长.类似练习3. 已知:如图7-82,AB是⊙O的直径,弦CD⊥AB于E,
M为AC上一点,AM的延长线交DC的延长线于F,
求证:∠AMD= ∠FMC
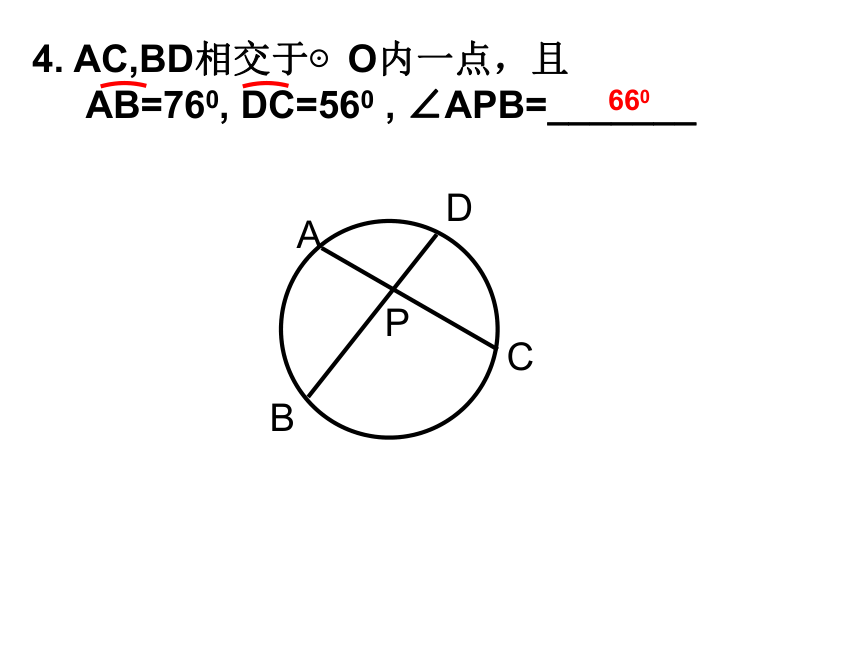
⌒提示:连结BC或连结AD均可。1.(08青海西宁)10.如图, ⊙O中,弦DC,AB的 延长线相交于点P,如果∠AOD=1200,∠BDC=250,那么∠P= .中考连接3502.(08山东泰安)如图,在⊙O中,∠AOB的度数为m,C是∠ACB上一点,D,E是AB弧上不同的两点(不与A,B两点重合),则∠D+∠E的度数为( )
A.m B. C. D.中考连接B3.如图AB是⊙O的直径,M是劣弧AC的中点,弦AC与BM相交于点D,∠ABC=2∠A,求证:AD=2DC。中考连接已知⊙O的半径OA=1,弦AB、AC的长分别是、则∠BAC的度数是______________。已知圆内接△ABC中,AB=AC,圆心O到BC距离为3cm,
圆半径为7cm,则腰长AB=_______ ,__________。750OCBANMAOCBMNABCHOABCOH分类讨论:(注意)150实际应用题:例1.一个圆形人工湖,弦AB是湖上的一座桥,已知桥AB长100m.测得圆周角∠C=45°求这个人工湖的直径.ABC一个圆形人工湖,弦AB是湖上的一座桥,已知桥AB长100m.测得圆周角∠C=45°求这个人工湖的直径.ABCD实际应用题: 例2.如图,在足球比赛中,甲、乙两名队员互相配合向对方球门MN进攻,当甲带球冲到A点时,乙已跟随冲到B点,此时自己直接射门好,还是迅速将球回传给乙,让乙射门好?
解: 考虑过M、N以及A、B中的任一点作一圆,这里不妨作出⊙BMN,显然,A点在⊙BMN外,设MA交圆于C,则
∠MAN<∠MCN,而∠MCN=∠MBN,
所以∠MAN<∠MBN.
因此,甲应将球回传给乙,让乙射门.例3. 船在航行过程中,船长常常通过测定角度来确定是否会遇到暗礁。如图A,B表示灯塔,暗礁分布在经过A,B两点的一个圆形区域内,C表示一个危险临界点,∠ACB就是“危险角”,当船与两个灯塔的夹角大于“危险角”时,就有可能触礁。弓形所含的圆周角∠C=50°,问船在航行时怎样才能保证不进入暗礁区?(1)当船与两个灯塔的夹角∠α大于“危险角”时,船位于哪个区域?为什么?(2)当船与两个灯塔的夹角∠α小于“危险角”时,船位于哪个区域?为什么?解:(1)当船与两个灯塔的夹角∠α大于“危险角” ∠C时,
船位于暗礁区域内(即⊙O内),理由是:
连结BE,假设船在(⊙O上,则有∠α=∠C,
这与∠α>∠C矛盾,所以船不可能在⊙O上;
假设船在⊙O外,则有∠α<∠AEB,即∠α<∠C,
这与∠α>∠C矛盾,所以船不可能在⊙O外.因此.
船只能位于⊙O内.
(2)当船与两个灯塔的夹角∠α小于“危险角” ∠C时,
船位于暗礁区域外(即⊙O外).
理由是:假设船在⊙O上,则有∠α=∠C,
这与∠α<∠C矛盾,所以船不可能在⊙O上;
假设船在⊙O内,则有∠α>∠AEB,即∠α>∠C.
这与∠α<∠C矛盾,所以船不可能在⊙O内,
因此,船只能位于⊙O外.
90°; 90°的圆周角所对的弦是圆的直径.3、圆的内接四边形对角互补。复习与巩固1.AB、AC为⊙O的两条弦,延长CA到D,使 AD=AB,如果∠ADB=35° ,
求∠BOC的度数是______1400210练一练3.如图,圆心角∠AOB=100°,则∠ACB=______。13006605.如图,∠A=28°,BE=BC=CD,则∠ACE的度数为( )
A.18° B.24° C.20° D.30°6.如图,AB是⊙O的直径,CD是弦,若AB=10cm,CD=6cm,
那么A、B两点到直线CD的距离之和为( )FDEABOCA.6cm B.8cm C.10cm D.12cmBB⌒⌒⌒7.已知:△ABC的三个顶点在⊙O上,∠BAC=50°,∠ABC=47°,求∠AOB.解:有题意知:∠A、∠B、∠C是圆周角,
∠AOB是圆心角.
又∵∠BAC=50°,∠ABC=47° ∴∠ACB=180°-(∠A+∠B)
=180°-(50°+47°)
=83°.∴ ∠AOB=2∠ACB=2×83°=166°.2009.11.6例1如图,P是△ABC的外接圆上的一点∠APC=∠CPB=60°。求证:△ABC是等边三角形证明:∵∠ABC和∠APC
都是⌒所对的圆周角。 AC∴∠ABC=∠APC=60°(同弧所对的圆周角相等)同理,∵∠BAC和∠CPB都是⌒所对的圆周角,BC∴∠BAC=∠CPB=60°。∴△ABC等边三角形。例2.如图OA、OB、OC都是⊙O的半径,∠AOB=2∠BOC.
求证:∠ACB=∠BAC.例3.求证:如果一个三角形一边上的中线等于这条边的一半,那么这个三角形是直角三角形。求证:△ABC是直角三角形。 已知:△ABC中,CD是AB边上的中线,CD= AB,CD是AB边上的中线
∵AD=BD 右∵AD=CD
∴∠A=∠ACD ∵BD=DC ∴∠DCB=∠B ∵∠A+∠ACD+∠DCB+∠B=180° 2∠ACD+2∠DAC=180° ∴∠BAD+∠DCB=90° ∴∠ACB=900
即三角形是直角三角形 例4.如图:AB是⊙O的直径,弦CD⊥AB于点E,G是⌒上任意一点,延长AG,与DC的延长线相交于点F,连接AD,GD,CG,找出图中所有和∠ADC相等的角,并说明理由.ACABDGFCEO1.如图7-59,AB是⊙O的直径,AB=2cm,
点C在圆周上,且∠BAC=30°,∠ABD=120°,
CD⊥BD于D.求BD的长.类似练习3. 已知:如图7-82,AB是⊙O的直径,弦CD⊥AB于E,
M为AC上一点,AM的延长线交DC的延长线于F,
求证:∠AMD= ∠FMC
⌒提示:连结BC或连结AD均可。1.(08青海西宁)10.如图, ⊙O中,弦DC,AB的 延长线相交于点P,如果∠AOD=1200,∠BDC=250,那么∠P= .中考连接3502.(08山东泰安)如图,在⊙O中,∠AOB的度数为m,C是∠ACB上一点,D,E是AB弧上不同的两点(不与A,B两点重合),则∠D+∠E的度数为( )
A.m B. C. D.中考连接B3.如图AB是⊙O的直径,M是劣弧AC的中点,弦AC与BM相交于点D,∠ABC=2∠A,求证:AD=2DC。中考连接已知⊙O的半径OA=1,弦AB、AC的长分别是、则∠BAC的度数是______________。已知圆内接△ABC中,AB=AC,圆心O到BC距离为3cm,
圆半径为7cm,则腰长AB=_______ ,__________。750OCBANMAOCBMNABCHOABCOH分类讨论:(注意)150实际应用题:例1.一个圆形人工湖,弦AB是湖上的一座桥,已知桥AB长100m.测得圆周角∠C=45°求这个人工湖的直径.ABC一个圆形人工湖,弦AB是湖上的一座桥,已知桥AB长100m.测得圆周角∠C=45°求这个人工湖的直径.ABCD实际应用题: 例2.如图,在足球比赛中,甲、乙两名队员互相配合向对方球门MN进攻,当甲带球冲到A点时,乙已跟随冲到B点,此时自己直接射门好,还是迅速将球回传给乙,让乙射门好?
解: 考虑过M、N以及A、B中的任一点作一圆,这里不妨作出⊙BMN,显然,A点在⊙BMN外,设MA交圆于C,则
∠MAN<∠MCN,而∠MCN=∠MBN,
所以∠MAN<∠MBN.
因此,甲应将球回传给乙,让乙射门.例3. 船在航行过程中,船长常常通过测定角度来确定是否会遇到暗礁。如图A,B表示灯塔,暗礁分布在经过A,B两点的一个圆形区域内,C表示一个危险临界点,∠ACB就是“危险角”,当船与两个灯塔的夹角大于“危险角”时,就有可能触礁。弓形所含的圆周角∠C=50°,问船在航行时怎样才能保证不进入暗礁区?(1)当船与两个灯塔的夹角∠α大于“危险角”时,船位于哪个区域?为什么?(2)当船与两个灯塔的夹角∠α小于“危险角”时,船位于哪个区域?为什么?解:(1)当船与两个灯塔的夹角∠α大于“危险角” ∠C时,
船位于暗礁区域内(即⊙O内),理由是:
连结BE,假设船在(⊙O上,则有∠α=∠C,
这与∠α>∠C矛盾,所以船不可能在⊙O上;
假设船在⊙O外,则有∠α<∠AEB,即∠α<∠C,
这与∠α>∠C矛盾,所以船不可能在⊙O外.因此.
船只能位于⊙O内.
(2)当船与两个灯塔的夹角∠α小于“危险角” ∠C时,
船位于暗礁区域外(即⊙O外).
理由是:假设船在⊙O上,则有∠α=∠C,
这与∠α<∠C矛盾,所以船不可能在⊙O上;
假设船在⊙O内,则有∠α>∠AEB,即∠α>∠C.
这与∠α<∠C矛盾,所以船不可能在⊙O内,
因此,船只能位于⊙O外.
同课章节目录
