正弦和余弦 第一课时课件

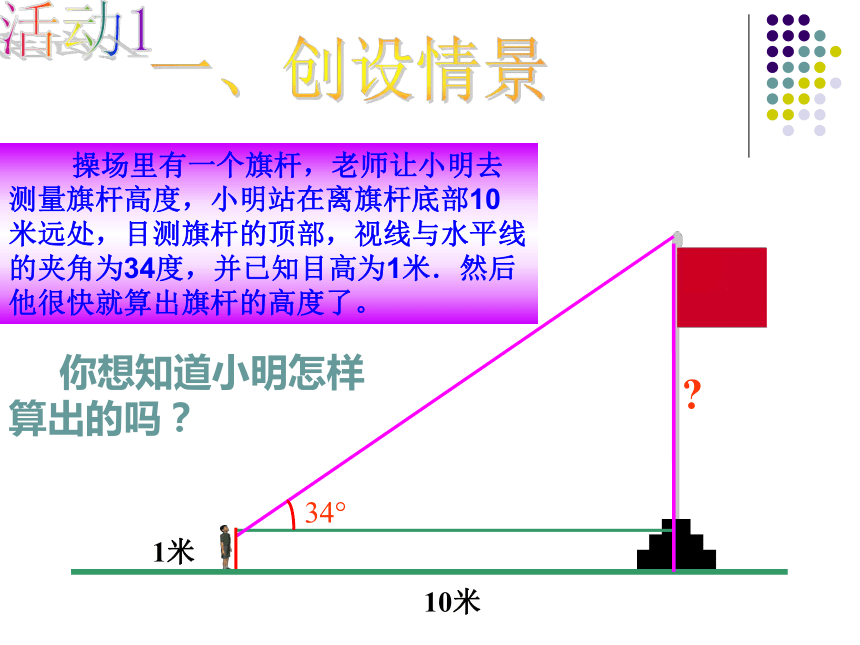
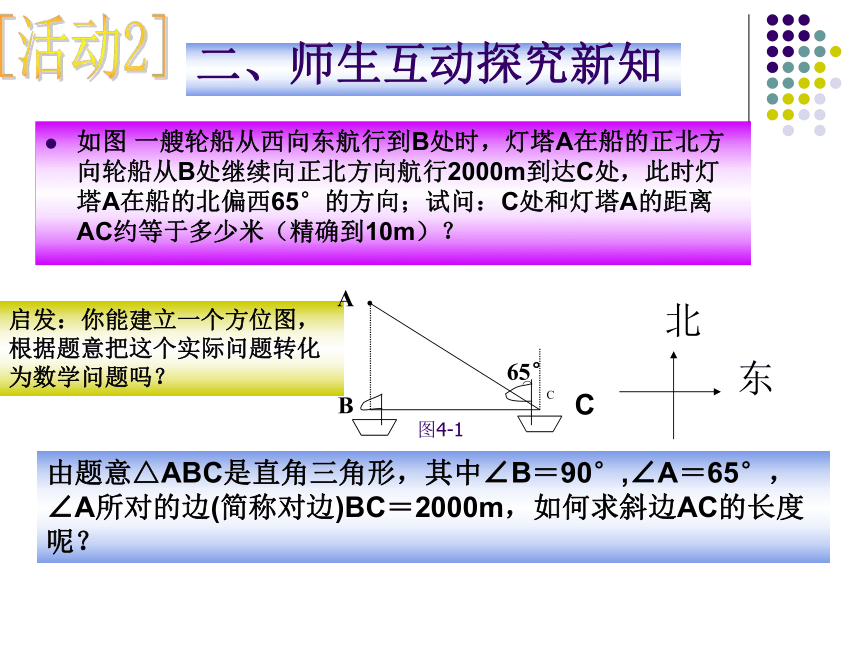
课件12张PPT。云场坪镇中学 龙琳锐角三角函数 操场里有一个旗杆，老师让小明去测量旗杆高度，小明站在离旗杆底部10米远处，目测旗杆的顶部，视线与水平线的夹角为34度，并已知目高为1米．然后他很快就算出旗杆的高度了。1米10米? 你想知道小明怎样算出的吗？一、创设情景活动1如图 一艘轮船从西向东航行到B处时，灯塔A在船的正北方向轮船从B处继续向正北方向航行2000m到达C处，此时灯塔A在船的北偏西65°的方向；试问：C处和灯塔A的距离AC约等于多少米（精确到10m）？北东启发：你能建立一个方位图，根据题意把这个实际问题转化为数学问题吗？C由题意△ABC是直角三角形，其中∠B＝90°,∠A＝65°，∠A所对的边(简称对边)BC＝2000m，如何求斜边AC的长度呢？[活动2]二、师生互动探究新知 图4-1上述问题就是：知道直角三角形的一个为65°的锐角和这个锐角的对边长度，想求斜边长度。
启发：能否使用已学的直角三角形的有关知识来解决？
为了解决这个问题，我们可以去探究在直角三角形中，65°角的对边与斜边的比值有什么规律？ (1)每位同学画一个直角三角形其中一个锐角为65°，量出65°角的对边长度和斜边长度，并计算:
＝？
(2) 与同桌和前后桌的同学交流计算结果，你有什么发现(精确到0. 01)？
由于各人画的直角三角形大小不一样，所以量得的长度也不一样，但比值为什么相等呢？
发现:在有一个锐角为65°的直角三角形中，65°角的对边与斜边的比值是一个常数，它约等于0.91。
[活动3]
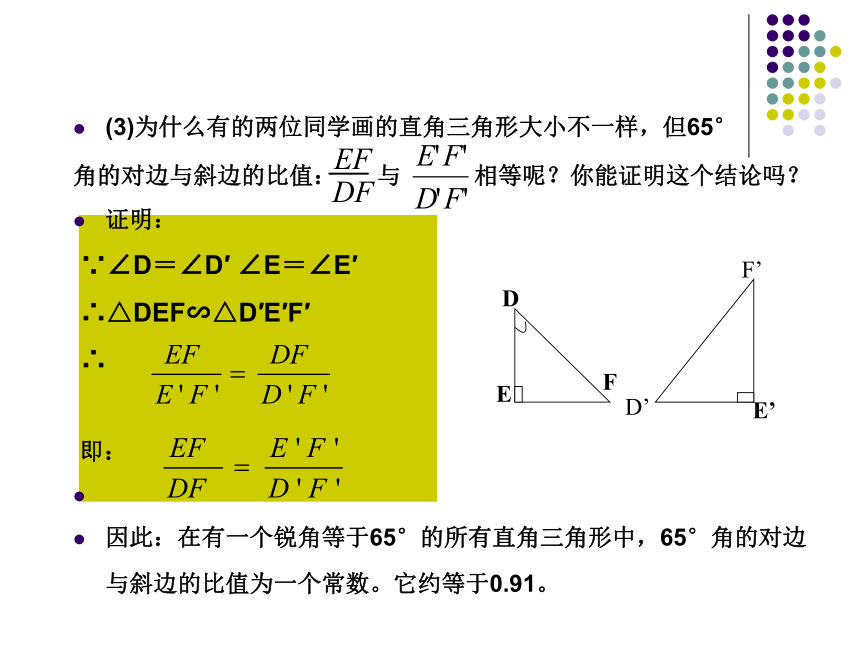
(3)为什么有的两位同学画的直角三角形大小不一样，但65°
角的对边与斜边的比值： 与 相等呢？你能证明这个结论吗？
证明：
∵∠D＝∠D′ ∠E＝∠E′
∴△DEF∽△D′E′F′
∴
即：

因此：在有一个锐角等于65°的所有直角三角形中，65°角的对边与斜边的比值为一个常数。它约等于0.91。 问:现在你能解决轮船航行到C处时与灯塔A的距离约等于多少米的问题吗？ 图4-1的直角三角形ABC中，BC=2000，∠A=65°，因此∠A的对边BC与斜边AC的比值应当等于上述常数，即
解得AC[活动4]图4-1类似的可以证明：在有一个锐角等于α的所有直角三角形中，角α的对边与斜边的比值为一个常数。
定义：在直角三角形中，锐角α的对边与斜边的比叫角α 的正弦（sine），记作Sinα 即
如图: 角α的对边 [活动5] 注意：1、sinα不是一个角；
2、sinα不是 sin与α的乘积 ；
3、sinα是一个比值 ； 4、sinα没有单位。Sinα读作sain α三、应用新知、解决问题 例1 如图 在直角三角形ABC中，∠C＝90°，BC=3，AB=5.
(1)求∠A的正弦SinA.
(2)求∠B的正弦SinB.
解：(1) ∠A的对边BC=3，斜边AB=5 ，
于是
SinA=
(2)∠B的对边是AC，根据勾股定理，得
AC2=AB2-BC2=52-32=16
于是 AC=4，
因此 SinB= 35[活动6]四、巩固提高深化认识
1、如图，在直角三角形ABC中，角C=90°,BC=5,AB=13。
(1)求sinA的值；
(2)求sinB的值。
解：
sinA=
sinB=
2、小刚说：对于任意锐角α，都有0＜sinα＜1你认为对吗？为什么？
答：小刚说得对。
∵
角α的对边是直角边，而直角边长小于斜边长。
∴ 0＜sinα＜1
513[活动7]五、回顾反思总结提炼 这节课我们主要学习了哪些知识？如图：
SinA= SinB= 六、课堂作业1、基础题（必做）：教科书 习题4.1第1题。
2、提高题（选做）：某人沿着坡角为65°的一斜坡从坡底向上走，当他沿坡面走了50米时，人上升了多少米？(精确1m