北师版七年级数学下册第二章单元练习(含答案)
文档属性
| 名称 | 北师版七年级数学下册第二章单元练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 105.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-04 00:00:00 | ||
图片预览



文档简介
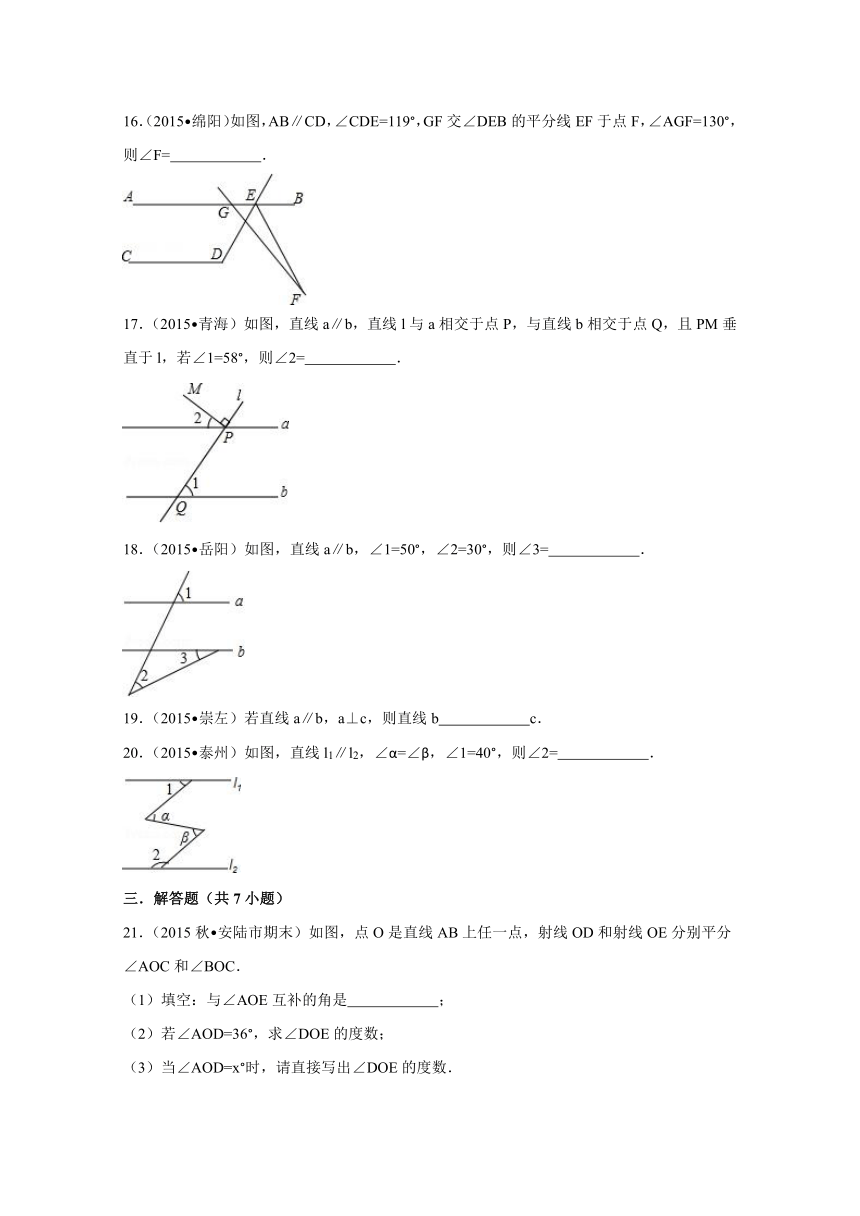
北师版七年级数学下册第二章单元练习
一.选择题(共12小题)
1.(2015?崇左)下列各图中,∠1与∠2互为余角的是( )
A. B. C. D.
2.(2015?百色)一个角的余角是这个角的补角的,则这个角的度数是( )
A.30° B.45° C.60° D.70°
3.(2015?厦门)如图,△ABC是锐角三角形,过点C作CD⊥AB,垂足为D,则点C到直线AB的距离是( )
A.线段CA的长 B.线段CD的长 C.线段AD的长 D.线段AB的长
4.(2014?汕尾)如图,能判定EB∥AC的条件是( )
A.∠C=∠ABE B.∠A=∠EBD C.∠C=∠ABC D.∠A=∠ABE
5.(2014?长春)如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=45°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转( )
A.15° B.30° C.45° D.60°
6.(2013?铜仁市)如图,在下列条件中,能判断AD∥BC的是( )
A.∠DAC=∠BCA B.∠DCB+∠ABC=180°
C.∠ABD=∠BDC D.∠BAC=∠ACD
7.(2013?抚顺)如图,直线l1、l2被直线l3、l4所截,下列条件中,不能判断直线l1∥l2的是( )
A.∠1=∠3 B.∠5=∠4 C.∠5+∠3=180° D.∠4+∠2=180°
8.(2015?重庆)如图,直线AB∥CD,直线EF分别与直线AB,CD相交于点G,H.若∠1=135°,则∠2的度数为( )
A.65° B.55° C.45° D.35°
9.(2015?湖北)如图,将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上.如果∠2=60°,那么∠1的度数为( )
A.60° B.50° C.40° D.30°
10.(2015?东莞)如图,直线a∥b,∠1=75°,∠2=35°,则∠3的度数是( )
A.75° B.55° C.40° D.35°
11.(2015?泸州)如图,AB∥CD,CB平分∠ABD.若∠C=40°,则∠D的度数为( )
A.90° B.100° C.110° D.120°
12.(2015?莱芜)如图,AB∥CD,EF平分∠AEG,若∠FGE=40°,那么∠EFG的度数为( )
A.35° B.40° C.70° D.140°
二.填空题(共9小题)
13.(2015?梧州)如图,已知直线AB与CD交于点O,ON平分∠DOB,若∠BOC=110°,则∠AON的度数为 度.
14.(2014?西藏)如图,点B、C、E在同一条直线上,请你写出一个能使AB∥CD成立的条件: .(只写一个即可,不添加任何字母或数字)
15.(2010?大田县)如图所示,已知∠C=100°,若增加一个条件,使得AB∥CD,试写出符合要求的一个条件 .
16.(2015?绵阳)如图,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=130°,则∠F= .
17.(2015?青海)如图,直线a∥b,直线l与a相交于点P,与直线b相交于点Q,且PM垂直于l,若∠1=58°,则∠2= .
18.(2015?岳阳)如图,直线a∥b,∠1=50°,∠2=30°,则∠3= .
19.(2015?崇左)若直线a∥b,a⊥c,则直线b c.
20.(2015?泰州)如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2= .
三.解答题(共7小题)
21.(2015秋?安陆市期末)如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.
(1)填空:与∠AOE互补的角是 ;
(2)若∠AOD=36°,求∠DOE的度数;
(3)当∠AOD=x°时,请直接写出∠DOE的度数.
22.(2015秋?商水县期末)已知一个角的补角比这个角的余角的3倍少18°,求这个角.
23.(2015秋?东莞校级月考)如图,∠B=42°,∠A+10°=∠ACB,∠ACD=64°.求证:AB∥CD.
24.(2014春?台安县月考)看图填空,并在括号内注明说理依据.
如图,已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,AC与BD平行吗?AE与BF平行吗?
解:因为∠1=35°,∠2=35°(已知),
所以∠1=∠2.
所以 ∥ ( ).
又因为AC⊥AE(已知),
所以∠EAC=90°.( )
所以∠EAB=∠EAC+∠1=125°.
同理可得,∠FBG=∠FBD+∠2= °.
所以∠EAB=∠FBG( ).
所以 ∥ (同位角相等,两直线平行).
25.(2015春?建昌县期末)已知:如图,AB∥CD,FE⊥AB于G,∠EMD=134°,求∠GEM的度数.
26.(2015春?临清市期末)如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D.
试说明:AC∥DF.
参考答案
一.选择题(共12小题)
1. C.2. B.3. B.4. D.5. A.6. A.7. B.8. C.9. D10. C.11. B.12. C.
二.填空题(共9小题)
13. 145. 14.∠1=∠2(答案不唯一).
15.∠BEC=180°﹣100°=80°(同旁内角互补两直线平行).
16. 9.5°. 17. 32°. 18. 20°. 19.⊥. 20. 140°.
三.解答题(共7小题)
21.解:(1)∵OE平分∠BOC,
∴∠BOE=∠COE;
∵∠AOE+∠BOE=180°,
∴∠AOE+∠COE=180°,
∴与∠AOE互补的角是∠BOE、∠COE;
故答案为∠BOE、∠COE;
(2)∵OD、OE分别平分∠AOC、∠BOC,
∴∠COD=∠AOD=36°,∠COE=∠BOE=∠BOC,
∴∠AOC=2×36°=72°,
∴∠BOC=180°﹣72°=108°,
∴∠COE=∠BOC=54°,
∴∠DOE=∠COD+∠COE=90°;
(3)当∠AOD=x°时,∠DOE=90°.
22.解:设这个角的度数为x°,则它的余角为(900﹣x°),补角为(1800﹣x°),
由题意得,180﹣x=3(90﹣x)﹣18,
解得,x=36,
答:这个角的度数为36°.
23.证明:∵∠A+∠ACB+∠B=180°,∠A+10°=∠ACB,
∴∠A+(∠A+10°)+∠B=180°
∴∠A=64°,
∵∠ACD=64°,
∴∠A=∠ACD,
∴AB∥CD(内错角相等,两直线平行).
24.解:因为∠1=35°,∠2=35°(已知),
所以∠1=∠2.
所以AC∥BD(同位角相等,两直线平行).
又因为AC⊥AE(已知),
所以∠EAC=90°.(垂直的定义)
所以∠EAB=∠EAC+∠1=125°.
同理可得,∠FBG=∠FBD+∠2=125°.
所以∠EAB=∠FBG(等量代换).
所以AE∥BF(同位角相等,两直线平行).
故答案为:AC;BD;同位角相等,两直线平行;垂直的定义;125;等量代换;AE;BF.
25.解:作EN∥CD,如图所示:
则∠EMD+∠MEN=180°,
∴∠MEN=180°﹣134°=46°,
∵FE⊥AB,
∴∠FGB=90°,
∵AB∥CD,
∴EN∥AB,
∴∠GEN=∠FGB=90°,
∴∠GEM=90°+46°=136°.
26.解:∵∠1=∠2(已知) (1分)
∠1=∠3( 对顶角相等 ) (2分)
∴∠2=∠3(等量代换) (3分)
∴DB∥EC ( 同位角相等,两直线平行 ) (5分)
∴∠C=∠ABD ( 两直线平行,同位角相等 ) (7分)
又∵∠C=∠D(已知) (8分)
∴∠D=∠ABD( 等量代换 ) (10分)
∴AC∥DF( 内错角相等,两直线平行 ) (12分)
一.选择题(共12小题)
1.(2015?崇左)下列各图中,∠1与∠2互为余角的是( )
A. B. C. D.
2.(2015?百色)一个角的余角是这个角的补角的,则这个角的度数是( )
A.30° B.45° C.60° D.70°
3.(2015?厦门)如图,△ABC是锐角三角形,过点C作CD⊥AB,垂足为D,则点C到直线AB的距离是( )
A.线段CA的长 B.线段CD的长 C.线段AD的长 D.线段AB的长
4.(2014?汕尾)如图,能判定EB∥AC的条件是( )
A.∠C=∠ABE B.∠A=∠EBD C.∠C=∠ABC D.∠A=∠ABE
5.(2014?长春)如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=45°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转( )
A.15° B.30° C.45° D.60°
6.(2013?铜仁市)如图,在下列条件中,能判断AD∥BC的是( )
A.∠DAC=∠BCA B.∠DCB+∠ABC=180°
C.∠ABD=∠BDC D.∠BAC=∠ACD
7.(2013?抚顺)如图,直线l1、l2被直线l3、l4所截,下列条件中,不能判断直线l1∥l2的是( )
A.∠1=∠3 B.∠5=∠4 C.∠5+∠3=180° D.∠4+∠2=180°
8.(2015?重庆)如图,直线AB∥CD,直线EF分别与直线AB,CD相交于点G,H.若∠1=135°,则∠2的度数为( )
A.65° B.55° C.45° D.35°
9.(2015?湖北)如图,将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上.如果∠2=60°,那么∠1的度数为( )
A.60° B.50° C.40° D.30°
10.(2015?东莞)如图,直线a∥b,∠1=75°,∠2=35°,则∠3的度数是( )
A.75° B.55° C.40° D.35°
11.(2015?泸州)如图,AB∥CD,CB平分∠ABD.若∠C=40°,则∠D的度数为( )
A.90° B.100° C.110° D.120°
12.(2015?莱芜)如图,AB∥CD,EF平分∠AEG,若∠FGE=40°,那么∠EFG的度数为( )
A.35° B.40° C.70° D.140°
二.填空题(共9小题)
13.(2015?梧州)如图,已知直线AB与CD交于点O,ON平分∠DOB,若∠BOC=110°,则∠AON的度数为 度.
14.(2014?西藏)如图,点B、C、E在同一条直线上,请你写出一个能使AB∥CD成立的条件: .(只写一个即可,不添加任何字母或数字)
15.(2010?大田县)如图所示,已知∠C=100°,若增加一个条件,使得AB∥CD,试写出符合要求的一个条件 .
16.(2015?绵阳)如图,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=130°,则∠F= .
17.(2015?青海)如图,直线a∥b,直线l与a相交于点P,与直线b相交于点Q,且PM垂直于l,若∠1=58°,则∠2= .
18.(2015?岳阳)如图,直线a∥b,∠1=50°,∠2=30°,则∠3= .
19.(2015?崇左)若直线a∥b,a⊥c,则直线b c.
20.(2015?泰州)如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2= .
三.解答题(共7小题)
21.(2015秋?安陆市期末)如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.
(1)填空:与∠AOE互补的角是 ;
(2)若∠AOD=36°,求∠DOE的度数;
(3)当∠AOD=x°时,请直接写出∠DOE的度数.
22.(2015秋?商水县期末)已知一个角的补角比这个角的余角的3倍少18°,求这个角.
23.(2015秋?东莞校级月考)如图,∠B=42°,∠A+10°=∠ACB,∠ACD=64°.求证:AB∥CD.
24.(2014春?台安县月考)看图填空,并在括号内注明说理依据.
如图,已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,AC与BD平行吗?AE与BF平行吗?
解:因为∠1=35°,∠2=35°(已知),
所以∠1=∠2.
所以 ∥ ( ).
又因为AC⊥AE(已知),
所以∠EAC=90°.( )
所以∠EAB=∠EAC+∠1=125°.
同理可得,∠FBG=∠FBD+∠2= °.
所以∠EAB=∠FBG( ).
所以 ∥ (同位角相等,两直线平行).
25.(2015春?建昌县期末)已知:如图,AB∥CD,FE⊥AB于G,∠EMD=134°,求∠GEM的度数.
26.(2015春?临清市期末)如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D.
试说明:AC∥DF.
参考答案
一.选择题(共12小题)
1. C.2. B.3. B.4. D.5. A.6. A.7. B.8. C.9. D10. C.11. B.12. C.
二.填空题(共9小题)
13. 145. 14.∠1=∠2(答案不唯一).
15.∠BEC=180°﹣100°=80°(同旁内角互补两直线平行).
16. 9.5°. 17. 32°. 18. 20°. 19.⊥. 20. 140°.
三.解答题(共7小题)
21.解:(1)∵OE平分∠BOC,
∴∠BOE=∠COE;
∵∠AOE+∠BOE=180°,
∴∠AOE+∠COE=180°,
∴与∠AOE互补的角是∠BOE、∠COE;
故答案为∠BOE、∠COE;
(2)∵OD、OE分别平分∠AOC、∠BOC,
∴∠COD=∠AOD=36°,∠COE=∠BOE=∠BOC,
∴∠AOC=2×36°=72°,
∴∠BOC=180°﹣72°=108°,
∴∠COE=∠BOC=54°,
∴∠DOE=∠COD+∠COE=90°;
(3)当∠AOD=x°时,∠DOE=90°.
22.解:设这个角的度数为x°,则它的余角为(900﹣x°),补角为(1800﹣x°),
由题意得,180﹣x=3(90﹣x)﹣18,
解得,x=36,
答:这个角的度数为36°.
23.证明:∵∠A+∠ACB+∠B=180°,∠A+10°=∠ACB,
∴∠A+(∠A+10°)+∠B=180°
∴∠A=64°,
∵∠ACD=64°,
∴∠A=∠ACD,
∴AB∥CD(内错角相等,两直线平行).
24.解:因为∠1=35°,∠2=35°(已知),
所以∠1=∠2.
所以AC∥BD(同位角相等,两直线平行).
又因为AC⊥AE(已知),
所以∠EAC=90°.(垂直的定义)
所以∠EAB=∠EAC+∠1=125°.
同理可得,∠FBG=∠FBD+∠2=125°.
所以∠EAB=∠FBG(等量代换).
所以AE∥BF(同位角相等,两直线平行).
故答案为:AC;BD;同位角相等,两直线平行;垂直的定义;125;等量代换;AE;BF.
25.解:作EN∥CD,如图所示:
则∠EMD+∠MEN=180°,
∴∠MEN=180°﹣134°=46°,
∵FE⊥AB,
∴∠FGB=90°,
∵AB∥CD,
∴EN∥AB,
∴∠GEN=∠FGB=90°,
∴∠GEM=90°+46°=136°.
26.解:∵∠1=∠2(已知) (1分)
∠1=∠3( 对顶角相等 ) (2分)
∴∠2=∠3(等量代换) (3分)
∴DB∥EC ( 同位角相等,两直线平行 ) (5分)
∴∠C=∠ABD ( 两直线平行,同位角相等 ) (7分)
又∵∠C=∠D(已知) (8分)
∴∠D=∠ABD( 等量代换 ) (10分)
∴AC∥DF( 内错角相等,两直线平行 ) (12分)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
