期末练习卷-2024-2025学年数学八年级上册苏科版(含答案)
文档属性
| 名称 | 期末练习卷-2024-2025学年数学八年级上册苏科版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 551.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-15 21:27:51 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末练习卷-2024-2025学年数学八年级上册苏科版
一.选择题(共8小题)
1.(2023秋 裕华区校级期末)用等式表示“81的平方根等于±9”,正确的是( )
A. B. C. D.
2.(2023秋 海口期末)如图,△ABC中,DE是AC的垂直平分线,若AE=3,△ABC的周长为19,则△ABD的周长为( )
A.13 B.14 C.15 D.16
3.(2023秋 东莞市校级期末)如图,AC、BD相交于点O,OA=OC,要使△AOB≌△COD,则下列添加的条件中,错误的是( )
A.∠A=∠C B.AB=CD C.OB=OD D.∠B=∠D
4.(2023秋 金安区校级期末)函数中,自变量x可取的值是( )
A.5 B.﹣3 C.0 D.1
5.(2023秋 雁塔区校级期末)已知一次函数y=3x+1与的图象交点坐标为(a,﹣1),则方程组的解是( )
A. B.
C. D.
6.(2023秋 仓山区校级期末)如图,在△ABC中,AD平分∠BAC,DF⊥AB于点F,E是线段BC的中点,若S△AEC=6,DF=2,AC=7.5,则AB的长是( )
A.3.5 B.4 C.4.5 D.5
7.(2023秋 蜀山区期末)如图,在△ABE和△BCD中,AB=BE=EA,BC=CD=DB,且两个三角形在线段AC同侧,则下列式子中错误的是( )
A.△ABD≌△EBC B.△NBC≌△MBD C.△ABM≌△EBN D.△AME≌△BCD
8.(2023秋 花山区校级期末)一辆快车将一批物资从乙地运往甲地送达后立即沿原路返回,且往返速度的大小不变,一辆慢车将一批物资从甲地运往乙地,两车离甲地的距离y(单位:km)与慢车行驶时间t(单位:h)的函数关系如图,下列不正确的是( )
A.慢车的速度为50km/h
B.快车的速度为150km/h
C.两车两次相遇间隔1.5h
D.两车两次相遇间隔1h
二.填空题(共9小题)
9.(2023秋 赤坎区校级期末)比较大小 (填“>”,“<”,“=”).
10.(2023秋 甘井子区校级期末)等腰三角形一个角为80°,它的另外两个角为 .
11.(2023秋 金台区期末)已知平面直角坐标系中,点P(3m,8)到坐标原点距离为10,则m的值为 .
12.(2023秋 侯马市期末)已知AB∥CD,请你添加一个条件,使得△CDA≌△ABC(不添加字母及辅助线),你添加的条件是 .
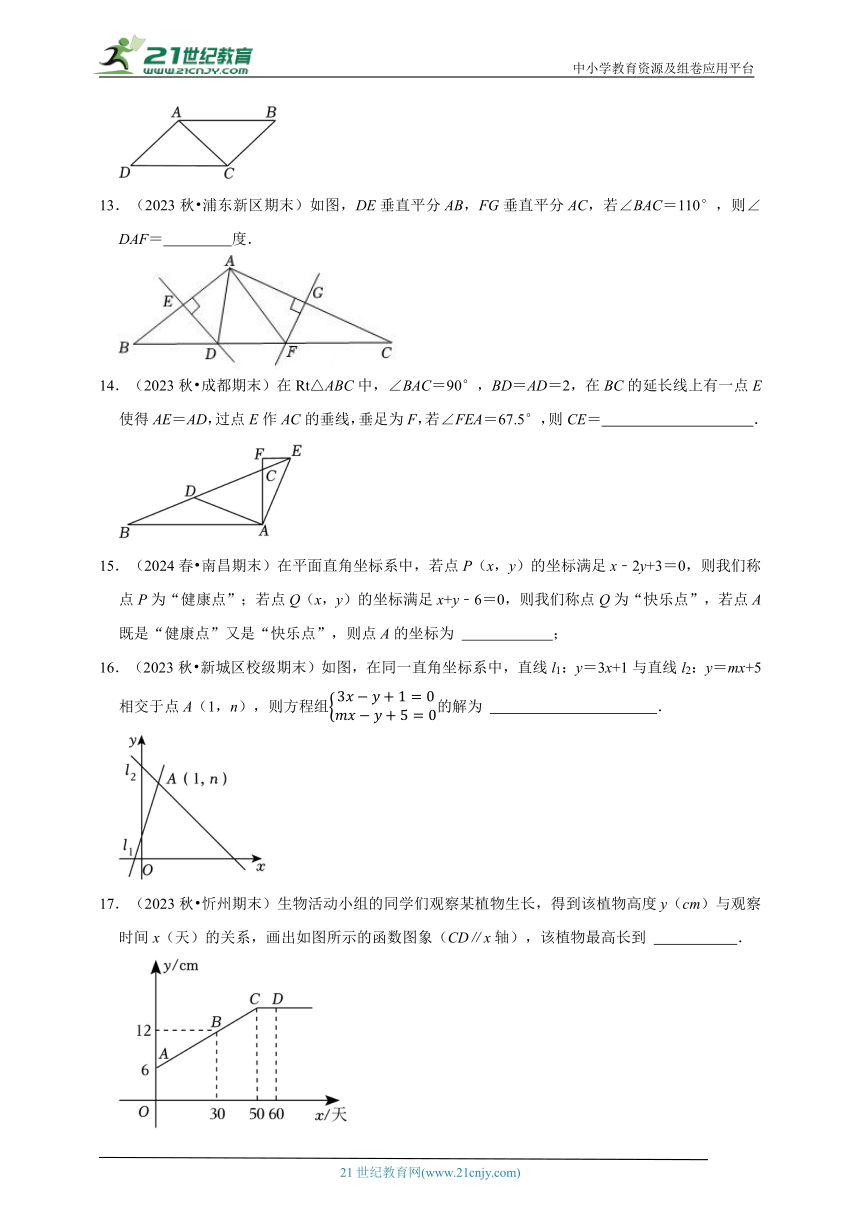
13.(2023秋 浦东新区期末)如图,DE垂直平分AB,FG垂直平分AC,若∠BAC=110°,则∠DAF= 度.
14.(2023秋 成都期末)在Rt△ABC中,∠BAC=90°,BD=AD=2,在BC的延长线上有一点E使得AE=AD,过点E作AC的垂线,垂足为F,若∠FEA=67.5°,则CE= .
15.(2024春 南昌期末)在平面直角坐标系中,若点P(x,y)的坐标满足x﹣2y+3=0,则我们称点P为“健康点”;若点Q(x,y)的坐标满足x+y﹣6=0,则我们称点Q为“快乐点”,若点A既是“健康点”又是“快乐点”,则点A的坐标为 ;
16.(2023秋 新城区校级期末)如图,在同一直角坐标系中,直线l1:y=3x+1与直线l2:y=mx+5相交于点A(1,n),则方程组的解为 .
17.(2023秋 忻州期末)生物活动小组的同学们观察某植物生长,得到该植物高度y(cm)与观察时间x(天)的关系,画出如图所示的函数图象(CD∥x轴),该植物最高长到 .
三.解答题(共8小题)
18.(2023秋 广陵区校级期末)求值:
(1)计算:;
(2)已知:(x﹣1)2=4,求x的值.
19.(2023秋 桐城市校级期末)如图,网格中小正方形的边长为1,△ABC在平面直角坐标系中的位置如图所示.
(1)求△ABC的面积;
(2)作出△ABC关于x轴对称的△A′B′C′,并直接写出A′,B′,C′三点的坐标.
20.(2023秋 常宁市期末)定义:如果一个三角形中有两个内角α,β满足α+2β=90°,那我们称这个三角形为“近直角三角形”.
(1)若△ABC是近直角三角形,∠B>90°,∠C=50°,则∠A= .
(2)在Rt△ABC中,∠BAC=90°,AB=3,AC=4,若CD是∠ACB的平分线.
①求证:△BDC为近直角三角形.
②求BD的长.
21.(2023秋 隆昌市校级期末)如图,在△ABC中,AD平分∠BAC交BC于点D,CE⊥AD,分别交AB、AD于点E、F.
(1)求证:EF=CF;
(2)若∠ACB=80°,∠BCE=30°,求∠ABC的度数.
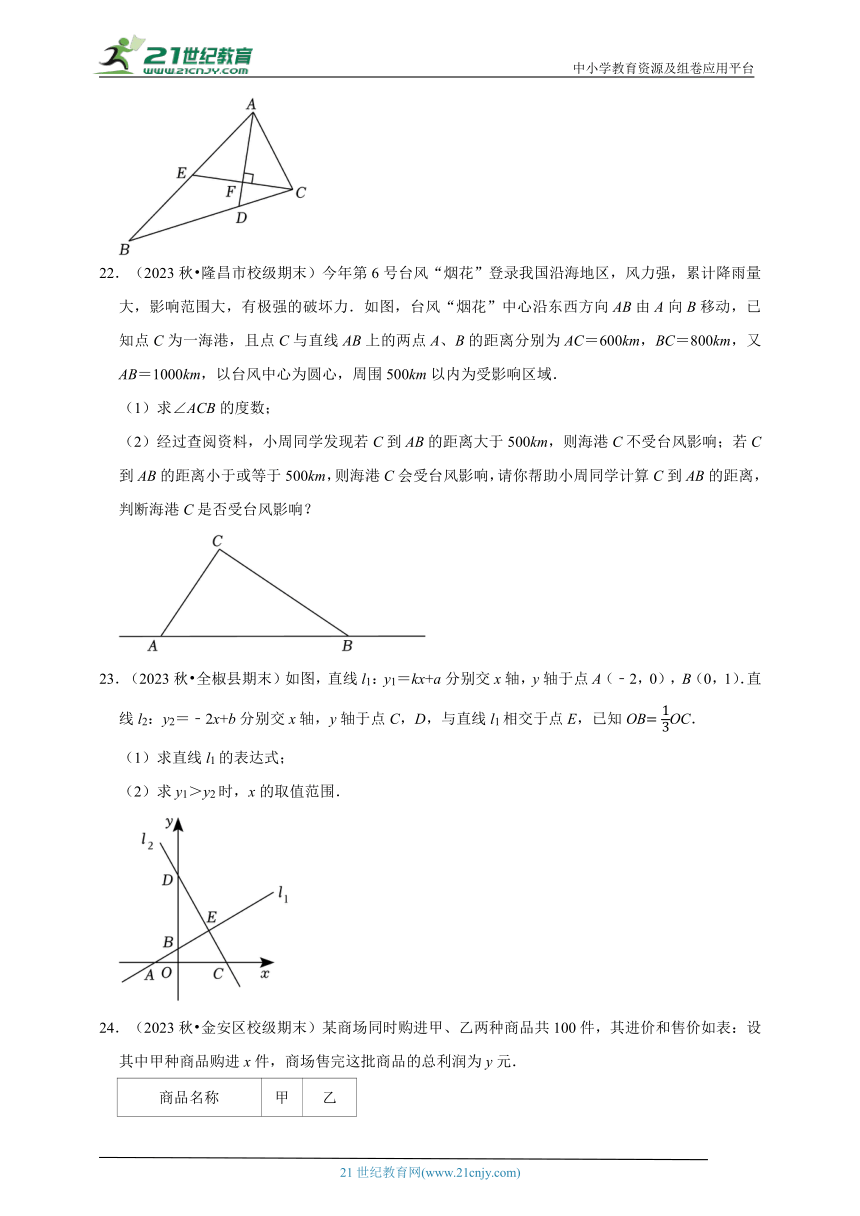
22.(2023秋 隆昌市校级期末)今年第6号台风“烟花”登录我国沿海地区,风力强,累计降雨量大,影响范围大,有极强的破坏力.如图,台风“烟花”中心沿东西方向AB由A向B移动,已知点C为一海港,且点C与直线AB上的两点A、B的距离分别为AC=600km,BC=800km,又AB=1000km,以台风中心为圆心,周围500km以内为受影响区域.
(1)求∠ACB的度数;
(2)经过查阅资料,小周同学发现若C到AB的距离大于500km,则海港C不受台风影响;若C到AB的距离小于或等于500km,则海港C会受台风影响,请你帮助小周同学计算C到AB的距离,判断海港C是否受台风影响?
23.(2023秋 全椒县期末)如图,直线l1:y1=kx+a分别交x轴,y轴于点A(﹣2,0),B(0,1).直线l2:y2=﹣2x+b分别交x轴,y轴于点C,D,与直线l1相交于点E,已知OBOC.
(1)求直线l1的表达式;
(2)求y1>y2时,x的取值范围.
24.(2023秋 金安区校级期末)某商场同时购进甲、乙两种商品共100件,其进价和售价如表:设其中甲种商品购进x件,商场售完这批商品的总利润为y元.
商品名称 甲 乙
进价(元/件) 40 90
售价(无/件) 60 120
(1)写出y关于x的函数关系式;
(2)该商品计划最多投入8000元用于购买这两种商品,则至少要购进多少件甲商品?若销售完这些商品,则商场可获得的最大利润是多少元?
25.(2023秋 金台区期末)如图,直线y=2x+4与x轴交于点A,与y轴交于点B,点C是OB的中点.
(1)求点C的坐标;
(2)求△ABC的面积;
(3)在坐标轴上是否存在一点P,使得△ABP是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
期末练习卷-2024-2025学年数学八年级上册苏科版
参考答案与试题解析
题号 1 2 3 4 5 6 7 8
答案 B A B A B C D D
一.选择题(共8小题)
1.(2023秋 裕华区校级期末)用等式表示“81的平方根等于±9”,正确的是( )
A. B. C. D.
【解答】解:用等式表示“81的平方根等于±9”为,
故选:B.
2.(2023秋 海口期末)如图,△ABC中,DE是AC的垂直平分线,若AE=3,△ABC的周长为19,则△ABD的周长为( )
A.13 B.14 C.15 D.16
【解答】解:∵DE是AC的垂直平分线,
∴AE=CE=3,AD=DC,
∴AC=6,
∵△ABC的周长为19,
∴AB+AC+BC=19,
∴AB+BC=13,
∴△ABD的周长为AB+BD+AD=AB+BD+DC=AB+BC=13,
故选:A.
3.(2023秋 东莞市校级期末)如图,AC、BD相交于点O,OA=OC,要使△AOB≌△COD,则下列添加的条件中,错误的是( )
A.∠A=∠C B.AB=CD C.OB=OD D.∠B=∠D
【解答】解:∵OA=OC,∠AOB=∠COD (对顶角相等),
∴A、如果添加∠A=∠C,则可根据ASA判定△AOB≌△COD;
B、如果添加 AB=CD,则根据SSA不能判定△AOB≌△COD;
C、如果添加 OB=OD,则可根据SAS判定△AOB≌△COD;
D、如果添加∠B=∠D,则可根据AAS判定△AOB≌△COD.
故选:B.
4.(2023秋 金安区校级期末)函数中,自变量x可取的值是( )
A.5 B.﹣3 C.0 D.1
【解答】解:由题意得:x﹣3≥0,
解得:x≥3,
则自变量x的可能取值是5,
故选:A.
5.(2023秋 雁塔区校级期末)已知一次函数y=3x+1与的图象交点坐标为(a,﹣1),则方程组的解是( )
A. B.
C. D.
【解答】解:∵一次函数y=3x+1与图象的交点的坐标是(a,﹣1),
∴3a+1=﹣1,
∴;
∵方程组即,
而的解为,
即方程组的解是.
故选:B.
6.(2023秋 仓山区校级期末)如图,在△ABC中,AD平分∠BAC,DF⊥AB于点F,E是线段BC的中点,若S△AEC=6,DF=2,AC=7.5,则AB的长是( )
A.3.5 B.4 C.4.5 D.5
【解答】解:如图,作DH⊥AC于H,
∵AD平分∠BAC,DF⊥AB,DH⊥AC,DE=2,
∴DF=DH=2,
∵E是线段BC的中点,
∴S△ABC=2S△AEC=2×6=12,
∴S△ABD+S△ACD=S△ABC=12,
∵,
∴,
解得AB=4.5,
故选:C.
7.(2023秋 蜀山区期末)如图,在△ABE和△BCD中,AB=BE=EA,BC=CD=DB,且两个三角形在线段AC同侧,则下列式子中错误的是( )
A.△ABD≌△EBC B.△NBC≌△MBD C.△ABM≌△EBN D.△AME≌△BCD
【解答】解:∵AB=BE=EA,BC=CD=DB,
∴△ABE和△BCD为等边三角形,
∴∠ABE=∠DBC=∠DCB=∠EBD=60°,
∴∠ABD=∠EBC=120°,
∵在△ABD和△EBC中,
,
∴△ABD≌△EBC(SAS),
∴∠ADB=∠ECB,
∵在△NBC和△MBD中,
,
∴△NBC≌△MBD(AAS),
∴BM=BN,
∵在△ABM和△EBN中,
,
∴△ABM≌△EBN(SAS),
△AME≌△BCD不一定成立,故D错误,符合题意.
故选:D.
8.(2023秋 花山区校级期末)一辆快车将一批物资从乙地运往甲地送达后立即沿原路返回,且往返速度的大小不变,一辆慢车将一批物资从甲地运往乙地,两车离甲地的距离y(单位:km)与慢车行驶时间t(单位:h)的函数关系如图,下列不正确的是( )
A.慢车的速度为50km/h
B.快车的速度为150km/h
C.两车两次相遇间隔1.5h
D.两车两次相遇间隔1h
【解答】解:根据图象可知,慢车的速度为300÷6=50(km/h),故A不符合题意;
对于快车,由于往返速度大小不变,总共行驶时间是4h,因此单程所花时间为2h,故其速度300÷2=150(km/h),故B不符合题意;
两车第一次相遇时,50x+150x=300,
解得x=1.5,
两车第二次相遇时,150(x﹣2)=50x,
解得x=3,
∴两车两次相遇间隔1.5h,故C不符合题意;D符合题意,
故选:D.
二.填空题(共9小题)
9.(2023秋 赤坎区校级期末)比较大小 < (填“>”,“<”,“=”).
【解答】解:∵,,
∴.
故答案为:<.
10.(2023秋 甘井子区校级期末)等腰三角形一个角为80°,它的另外两个角为 80°,20°或50°,50° .
【解答】解:①当这个角是底角时,另外两个角是:80°,20°;
②当这个角是顶角时,另外两个角是:50°,50°.
故答案为:80°,20°或50°,50°.
11.(2023秋 金台区期末)已知平面直角坐标系中,点P(3m,8)到坐标原点距离为10,则m的值为 ±2 .
【解答】解:∵点P(3m,8)到坐标原点距离为10,
∴10,
解得m=±2,
故答案为:±2.
12.(2023秋 侯马市期末)已知AB∥CD,请你添加一个条件,使得△CDA≌△ABC(不添加字母及辅助线),你添加的条件是 AB=CD(答案不唯一) .
【解答】证明:∵AB∥CD,
∴∠ACD=∠CAB,
在△CDA和△ABC中,
,
∴△CDA≌△ABC(SAS),
∴添加一个条件AB=CD(答案不唯一),使得△CDA≌△ABC.
故答案为:AB=CD(答案不唯一).
13.(2023秋 浦东新区期末)如图,DE垂直平分AB,FG垂直平分AC,若∠BAC=110°,则∠DAF= 40 度.
【解答】解:∵∠BAC=110°,
∴∠B+∠C=180°﹣∠BAC=180°﹣110°=70°,
∵DE垂直平分AB,
∴DA=DB,
∴∠DAB=∠B,
同理可得:∠PAC=∠C,
∴∠DAB+∠PAC=∠B+∠C=70°,
∴∠DAF=110°﹣70°=40°,
故答案为:40.
14.(2023秋 成都期末)在Rt△ABC中,∠BAC=90°,BD=AD=2,在BC的延长线上有一点E使得AE=AD,过点E作AC的垂线,垂足为F,若∠FEA=67.5°,则CE= 22 .
【解答】解:∵BD=AD,
∴∠B=∠BAD,
∴∠ADE=∠B+∠BAD=2∠B,
∵AD=AE,
∴∠AED=∠ADE=2∠B,
∵EF⊥AF,BA⊥AF,
∴EF∥AB,
∠CEF=∠B,
∴∠AEF=∠AEC+∠CEF=3∠B=67.5°,
∴∠B=22.5°,
∴∠ADE=45°,
∵∠AED=∠ADE=45°,
∴△ADE是等腰直角三角形,
∴DE2,
∵∠BAC=90°,
∴∠B+∠ACD=∠BAD+∠DAC=90°,
∴∠ACD=∠DAC,
∴DC=AD=2,
∴CE=DE﹣CD=22.
故答案为:22.
15.(2024春 南昌期末)在平面直角坐标系中,若点P(x,y)的坐标满足x﹣2y+3=0,则我们称点P为“健康点”;若点Q(x,y)的坐标满足x+y﹣6=0,则我们称点Q为“快乐点”,若点A既是“健康点”又是“快乐点”,则点A的坐标为 (3,3) ;
【解答】解:点A既是“健康点”又是“快乐点”,则A坐标应该满足x﹣2y+3=0和x+y﹣6=0,
解
得:,
∴A的坐标为(3,3);
故答案为:(3,3).
16.(2023秋 新城区校级期末)如图,在同一直角坐标系中,直线l1:y=3x+1与直线l2:y=mx+5相交于点A(1,n),则方程组的解为 .
【解答】解:∵直线l1:y=3x+1与直线l2:y=mx+5相交于点A(1,n),
∴n=3×1+1=4,
∴A(1,4),
∴方程组的解为.
故答案为:
17.(2023秋 忻州期末)生物活动小组的同学们观察某植物生长,得到该植物高度y(cm)与观察时间x(天)的关系,画出如图所示的函数图象(CD∥x轴),该植物最高长到 16cm .
【解答】解:设AC的函数关系式为y=kx+b(k、b为常数,且k≠0).
将A(0,6)和B(30,12)代入y=kx+b,
得,解得,
∴AC的函数关系式为yx+6(0≤x≤50).
当x=50时,yx+650+6=16,
∴该植物最高长到16cm.
故答案为:16cm.
三.解答题(共8小题)
18.(2023秋 广陵区校级期末)求值:
(1)计算:;
(2)已知:(x﹣1)2=4,求x的值.
【解答】解:(1)
;
(2)∵(x﹣1)2=4,
∴,
解得:x=3或x=﹣1.
19.(2023秋 桐城市校级期末)如图,网格中小正方形的边长为1,△ABC在平面直角坐标系中的位置如图所示.
(1)求△ABC的面积;
(2)作出△ABC关于x轴对称的△A′B′C′,并直接写出A′,B′,C′三点的坐标.
【解答】解:(1)依题意,
,
∴△ABC的面积为;
(2)如图:
∴A′,B′,C′三点的坐标分别是(4,﹣3),(3,﹣1),(1,﹣2),
20.(2023秋 常宁市期末)定义:如果一个三角形中有两个内角α,β满足α+2β=90°,那我们称这个三角形为“近直角三角形”.
(1)若△ABC是近直角三角形,∠B>90°,∠C=50°,则∠A= 20° .
(2)在Rt△ABC中,∠BAC=90°,AB=3,AC=4,若CD是∠ACB的平分线.
①求证:△BDC为近直角三角形.
②求BD的长.
【解答】解:(1)∠B不可能是α或β,
当∠A=α时,∠C=β=50°,α+2β=90°,不成立;
故∠A=β,∠C=α,α+2β=90°,则β=20°,
故答案为:20°;
(2)①如图1,设∠ACD=∠DCB=β,∠B=α,
则α+2β=90°,故△BDC是“近直角三角形”;
②如图2,过点D作DM⊥BC于点M,
∵CD平分∠ACB,DM⊥BC,DA⊥CA,
∴AD=DM.
在Rt△ACD和Rt△MCD中,
,
∴Rt△ACD≌Rt△MCD(HL).
∴AC=CM=4.
∵AB=3,AC=4,
∴BC5.
∴BM=1.
设AD=DM=x,
∵DM2+BM2=DB2,
∴x2+12=(3﹣x)2,
∴x,
∴BD=AB﹣AD=3.
21.(2023秋 隆昌市校级期末)如图,在△ABC中,AD平分∠BAC交BC于点D,CE⊥AD,分别交AB、AD于点E、F.
(1)求证:EF=CF;
(2)若∠ACB=80°,∠BCE=30°,求∠ABC的度数.
【解答】(1)证明:∵AD平分∠BAC,CE⊥AD,
∴∠EAF=∠CAF,∠AFE=∠AFC=90°,
在△AFE和△AFC中,
,
∴△AFE≌△AFC(ASA),
∴EF=CF;
(2)解:由(1)可得△AFE≌△AFC,
∴∠AEC=∠ACE,
∵∠ACB=80°,∠BCE=30°,
∴∠AEC=∠ACE=∠ACB﹣∠BCE=50°,
∴∠ABC=∠AEC﹣∠BCE=20°.
22.(2023秋 隆昌市校级期末)今年第6号台风“烟花”登录我国沿海地区,风力强,累计降雨量大,影响范围大,有极强的破坏力.如图,台风“烟花”中心沿东西方向AB由A向B移动,已知点C为一海港,且点C与直线AB上的两点A、B的距离分别为AC=600km,BC=800km,又AB=1000km,以台风中心为圆心,周围500km以内为受影响区域.
(1)求∠ACB的度数;
(2)经过查阅资料,小周同学发现若C到AB的距离大于500km,则海港C不受台风影响;若C到AB的距离小于或等于500km,则海港C会受台风影响,请你帮助小周同学计算C到AB的距离,判断海港C是否受台风影响?
【解答】解:(1)∵AC=600km,BC=800km,AB=1000km,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠ACB=90°;
(2)海港C受台风影响,理由如下:
过点C作CD⊥AB于点D,
∵△ABC是直角三角形,
∴AC BCCD AB,
∴CD480(km),
∵480km<500km,
∴海港C会受台风影响.
23.(2023秋 全椒县期末)如图,直线l1:y1=kx+a分别交x轴,y轴于点A(﹣2,0),B(0,1).直线l2:y2=﹣2x+b分别交x轴,y轴于点C,D,与直线l1相交于点E,已知OBOC.
(1)求直线l1的表达式;
(2)求y1>y2时,x的取值范围.
【解答】解:(1)根据题意得,
解得,
∴直线l1的表达式为y1x+1;
(2)∵B(0,1),
∴OB=1,
∵OBOC,
∴OC=3OB=3,
∴C(3,0),
把C(3,0)代入y2=﹣2x+b得﹣6+b=0,
解得b=6,
∴y2=﹣2x+6,
解不等式x+1>﹣2x+6得x>2,
即y1>y2时,x的取值范围为x>2.
24.(2023秋 金安区校级期末)某商场同时购进甲、乙两种商品共100件,其进价和售价如表:设其中甲种商品购进x件,商场售完这批商品的总利润为y元.
商品名称 甲 乙
进价(元/件) 40 90
售价(无/件) 60 120
(1)写出y关于x的函数关系式;
(2)该商品计划最多投入8000元用于购买这两种商品,则至少要购进多少件甲商品?若销售完这些商品,则商场可获得的最大利润是多少元?
【解答】解:(1)由题意得y=(60﹣40)x+(120﹣90)×(100﹣x)=﹣10x+3000,
∴y与x的函数关系式为y=﹣10x+3000.
(2)由题意得40x+90×(100﹣x)≤8000,
解得x≥20,
∵y=﹣10x+3000,
∴y随x的增大而减小,
∴当x=20时,利润最大且ymax=2800,
∴若售完这些商品,则至少购进20件甲商品商场可获得最大利润,获得的最大利润是2800元.
25.(2023秋 金台区期末)如图,直线y=2x+4与x轴交于点A,与y轴交于点B,点C是OB的中点.
(1)求点C的坐标;
(2)求△ABC的面积;
(3)在坐标轴上是否存在一点P,使得△ABP是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
【解答】解:(1)∵y=2x+4与y轴交于点B,
当x=0时,y=2×0+4=4,则B(0,4),
∴OB=4,
∵点C是OB的中点,
∴BC=OC=2,
∴C(0,2);
(2)当y=0时,2x+4=0,
∴x=﹣2,
∴OA=2,
∴S△ABCCB×AO2×2=2;
(3)分两种情况:
i)设x轴上存在一点P(m,0),使得△ABP是直角三角形,
∵A(﹣2,0),B(0,4),∠AOB=90°,
根据勾股定理可得:AB2=OB2+OA2,
∴AB2=42+22=20,
∵AP2=(m+2)2,BP2=m2+16,
△ABP是直角三角形,分两种情况:
①∠APB=90°时,P与原点重合,此时P(0,0);
②∠ABP=90°时,则AB2+BP2=AP2,
∴20+m2+16=(m+2)2,
解得:m=8,此时P(8,0);
ii)设y轴上存在一点P(0,n),使得△ABP是直角三角形,
∵AB2=20,BP2=(n﹣4)2,AP2=n2+4,
当∠BAP=90°时,则AB2+AP2=BP2,
∴20+4+n2=(n﹣4)2,
解得:n=﹣1,此时P(0,﹣1);
综上所述:P(0,0)或(8,0)或(0,﹣1).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末练习卷-2024-2025学年数学八年级上册苏科版
一.选择题(共8小题)
1.(2023秋 裕华区校级期末)用等式表示“81的平方根等于±9”,正确的是( )
A. B. C. D.
2.(2023秋 海口期末)如图,△ABC中,DE是AC的垂直平分线,若AE=3,△ABC的周长为19,则△ABD的周长为( )
A.13 B.14 C.15 D.16
3.(2023秋 东莞市校级期末)如图,AC、BD相交于点O,OA=OC,要使△AOB≌△COD,则下列添加的条件中,错误的是( )
A.∠A=∠C B.AB=CD C.OB=OD D.∠B=∠D
4.(2023秋 金安区校级期末)函数中,自变量x可取的值是( )
A.5 B.﹣3 C.0 D.1
5.(2023秋 雁塔区校级期末)已知一次函数y=3x+1与的图象交点坐标为(a,﹣1),则方程组的解是( )
A. B.
C. D.
6.(2023秋 仓山区校级期末)如图,在△ABC中,AD平分∠BAC,DF⊥AB于点F,E是线段BC的中点,若S△AEC=6,DF=2,AC=7.5,则AB的长是( )
A.3.5 B.4 C.4.5 D.5
7.(2023秋 蜀山区期末)如图,在△ABE和△BCD中,AB=BE=EA,BC=CD=DB,且两个三角形在线段AC同侧,则下列式子中错误的是( )
A.△ABD≌△EBC B.△NBC≌△MBD C.△ABM≌△EBN D.△AME≌△BCD
8.(2023秋 花山区校级期末)一辆快车将一批物资从乙地运往甲地送达后立即沿原路返回,且往返速度的大小不变,一辆慢车将一批物资从甲地运往乙地,两车离甲地的距离y(单位:km)与慢车行驶时间t(单位:h)的函数关系如图,下列不正确的是( )
A.慢车的速度为50km/h
B.快车的速度为150km/h
C.两车两次相遇间隔1.5h
D.两车两次相遇间隔1h
二.填空题(共9小题)
9.(2023秋 赤坎区校级期末)比较大小 (填“>”,“<”,“=”).
10.(2023秋 甘井子区校级期末)等腰三角形一个角为80°,它的另外两个角为 .
11.(2023秋 金台区期末)已知平面直角坐标系中,点P(3m,8)到坐标原点距离为10,则m的值为 .
12.(2023秋 侯马市期末)已知AB∥CD,请你添加一个条件,使得△CDA≌△ABC(不添加字母及辅助线),你添加的条件是 .
13.(2023秋 浦东新区期末)如图,DE垂直平分AB,FG垂直平分AC,若∠BAC=110°,则∠DAF= 度.
14.(2023秋 成都期末)在Rt△ABC中,∠BAC=90°,BD=AD=2,在BC的延长线上有一点E使得AE=AD,过点E作AC的垂线,垂足为F,若∠FEA=67.5°,则CE= .
15.(2024春 南昌期末)在平面直角坐标系中,若点P(x,y)的坐标满足x﹣2y+3=0,则我们称点P为“健康点”;若点Q(x,y)的坐标满足x+y﹣6=0,则我们称点Q为“快乐点”,若点A既是“健康点”又是“快乐点”,则点A的坐标为 ;
16.(2023秋 新城区校级期末)如图,在同一直角坐标系中,直线l1:y=3x+1与直线l2:y=mx+5相交于点A(1,n),则方程组的解为 .
17.(2023秋 忻州期末)生物活动小组的同学们观察某植物生长,得到该植物高度y(cm)与观察时间x(天)的关系,画出如图所示的函数图象(CD∥x轴),该植物最高长到 .
三.解答题(共8小题)
18.(2023秋 广陵区校级期末)求值:
(1)计算:;
(2)已知:(x﹣1)2=4,求x的值.
19.(2023秋 桐城市校级期末)如图,网格中小正方形的边长为1,△ABC在平面直角坐标系中的位置如图所示.
(1)求△ABC的面积;
(2)作出△ABC关于x轴对称的△A′B′C′,并直接写出A′,B′,C′三点的坐标.
20.(2023秋 常宁市期末)定义:如果一个三角形中有两个内角α,β满足α+2β=90°,那我们称这个三角形为“近直角三角形”.
(1)若△ABC是近直角三角形,∠B>90°,∠C=50°,则∠A= .
(2)在Rt△ABC中,∠BAC=90°,AB=3,AC=4,若CD是∠ACB的平分线.
①求证:△BDC为近直角三角形.
②求BD的长.
21.(2023秋 隆昌市校级期末)如图,在△ABC中,AD平分∠BAC交BC于点D,CE⊥AD,分别交AB、AD于点E、F.
(1)求证:EF=CF;
(2)若∠ACB=80°,∠BCE=30°,求∠ABC的度数.
22.(2023秋 隆昌市校级期末)今年第6号台风“烟花”登录我国沿海地区,风力强,累计降雨量大,影响范围大,有极强的破坏力.如图,台风“烟花”中心沿东西方向AB由A向B移动,已知点C为一海港,且点C与直线AB上的两点A、B的距离分别为AC=600km,BC=800km,又AB=1000km,以台风中心为圆心,周围500km以内为受影响区域.
(1)求∠ACB的度数;
(2)经过查阅资料,小周同学发现若C到AB的距离大于500km,则海港C不受台风影响;若C到AB的距离小于或等于500km,则海港C会受台风影响,请你帮助小周同学计算C到AB的距离,判断海港C是否受台风影响?
23.(2023秋 全椒县期末)如图,直线l1:y1=kx+a分别交x轴,y轴于点A(﹣2,0),B(0,1).直线l2:y2=﹣2x+b分别交x轴,y轴于点C,D,与直线l1相交于点E,已知OBOC.
(1)求直线l1的表达式;
(2)求y1>y2时,x的取值范围.
24.(2023秋 金安区校级期末)某商场同时购进甲、乙两种商品共100件,其进价和售价如表:设其中甲种商品购进x件,商场售完这批商品的总利润为y元.
商品名称 甲 乙
进价(元/件) 40 90
售价(无/件) 60 120
(1)写出y关于x的函数关系式;
(2)该商品计划最多投入8000元用于购买这两种商品,则至少要购进多少件甲商品?若销售完这些商品,则商场可获得的最大利润是多少元?
25.(2023秋 金台区期末)如图,直线y=2x+4与x轴交于点A,与y轴交于点B,点C是OB的中点.
(1)求点C的坐标;
(2)求△ABC的面积;
(3)在坐标轴上是否存在一点P,使得△ABP是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
期末练习卷-2024-2025学年数学八年级上册苏科版
参考答案与试题解析
题号 1 2 3 4 5 6 7 8
答案 B A B A B C D D
一.选择题(共8小题)
1.(2023秋 裕华区校级期末)用等式表示“81的平方根等于±9”,正确的是( )
A. B. C. D.
【解答】解:用等式表示“81的平方根等于±9”为,
故选:B.
2.(2023秋 海口期末)如图,△ABC中,DE是AC的垂直平分线,若AE=3,△ABC的周长为19,则△ABD的周长为( )
A.13 B.14 C.15 D.16
【解答】解:∵DE是AC的垂直平分线,
∴AE=CE=3,AD=DC,
∴AC=6,
∵△ABC的周长为19,
∴AB+AC+BC=19,
∴AB+BC=13,
∴△ABD的周长为AB+BD+AD=AB+BD+DC=AB+BC=13,
故选:A.
3.(2023秋 东莞市校级期末)如图,AC、BD相交于点O,OA=OC,要使△AOB≌△COD,则下列添加的条件中,错误的是( )
A.∠A=∠C B.AB=CD C.OB=OD D.∠B=∠D
【解答】解:∵OA=OC,∠AOB=∠COD (对顶角相等),
∴A、如果添加∠A=∠C,则可根据ASA判定△AOB≌△COD;
B、如果添加 AB=CD,则根据SSA不能判定△AOB≌△COD;
C、如果添加 OB=OD,则可根据SAS判定△AOB≌△COD;
D、如果添加∠B=∠D,则可根据AAS判定△AOB≌△COD.
故选:B.
4.(2023秋 金安区校级期末)函数中,自变量x可取的值是( )
A.5 B.﹣3 C.0 D.1
【解答】解:由题意得:x﹣3≥0,
解得:x≥3,
则自变量x的可能取值是5,
故选:A.
5.(2023秋 雁塔区校级期末)已知一次函数y=3x+1与的图象交点坐标为(a,﹣1),则方程组的解是( )
A. B.
C. D.
【解答】解:∵一次函数y=3x+1与图象的交点的坐标是(a,﹣1),
∴3a+1=﹣1,
∴;
∵方程组即,
而的解为,
即方程组的解是.
故选:B.
6.(2023秋 仓山区校级期末)如图,在△ABC中,AD平分∠BAC,DF⊥AB于点F,E是线段BC的中点,若S△AEC=6,DF=2,AC=7.5,则AB的长是( )
A.3.5 B.4 C.4.5 D.5
【解答】解:如图,作DH⊥AC于H,
∵AD平分∠BAC,DF⊥AB,DH⊥AC,DE=2,
∴DF=DH=2,
∵E是线段BC的中点,
∴S△ABC=2S△AEC=2×6=12,
∴S△ABD+S△ACD=S△ABC=12,
∵,
∴,
解得AB=4.5,
故选:C.
7.(2023秋 蜀山区期末)如图,在△ABE和△BCD中,AB=BE=EA,BC=CD=DB,且两个三角形在线段AC同侧,则下列式子中错误的是( )
A.△ABD≌△EBC B.△NBC≌△MBD C.△ABM≌△EBN D.△AME≌△BCD
【解答】解:∵AB=BE=EA,BC=CD=DB,
∴△ABE和△BCD为等边三角形,
∴∠ABE=∠DBC=∠DCB=∠EBD=60°,
∴∠ABD=∠EBC=120°,
∵在△ABD和△EBC中,
,
∴△ABD≌△EBC(SAS),
∴∠ADB=∠ECB,
∵在△NBC和△MBD中,
,
∴△NBC≌△MBD(AAS),
∴BM=BN,
∵在△ABM和△EBN中,
,
∴△ABM≌△EBN(SAS),
△AME≌△BCD不一定成立,故D错误,符合题意.
故选:D.
8.(2023秋 花山区校级期末)一辆快车将一批物资从乙地运往甲地送达后立即沿原路返回,且往返速度的大小不变,一辆慢车将一批物资从甲地运往乙地,两车离甲地的距离y(单位:km)与慢车行驶时间t(单位:h)的函数关系如图,下列不正确的是( )
A.慢车的速度为50km/h
B.快车的速度为150km/h
C.两车两次相遇间隔1.5h
D.两车两次相遇间隔1h
【解答】解:根据图象可知,慢车的速度为300÷6=50(km/h),故A不符合题意;
对于快车,由于往返速度大小不变,总共行驶时间是4h,因此单程所花时间为2h,故其速度300÷2=150(km/h),故B不符合题意;
两车第一次相遇时,50x+150x=300,
解得x=1.5,
两车第二次相遇时,150(x﹣2)=50x,
解得x=3,
∴两车两次相遇间隔1.5h,故C不符合题意;D符合题意,
故选:D.
二.填空题(共9小题)
9.(2023秋 赤坎区校级期末)比较大小 < (填“>”,“<”,“=”).
【解答】解:∵,,
∴.
故答案为:<.
10.(2023秋 甘井子区校级期末)等腰三角形一个角为80°,它的另外两个角为 80°,20°或50°,50° .
【解答】解:①当这个角是底角时,另外两个角是:80°,20°;
②当这个角是顶角时,另外两个角是:50°,50°.
故答案为:80°,20°或50°,50°.
11.(2023秋 金台区期末)已知平面直角坐标系中,点P(3m,8)到坐标原点距离为10,则m的值为 ±2 .
【解答】解:∵点P(3m,8)到坐标原点距离为10,
∴10,
解得m=±2,
故答案为:±2.
12.(2023秋 侯马市期末)已知AB∥CD,请你添加一个条件,使得△CDA≌△ABC(不添加字母及辅助线),你添加的条件是 AB=CD(答案不唯一) .
【解答】证明:∵AB∥CD,
∴∠ACD=∠CAB,
在△CDA和△ABC中,
,
∴△CDA≌△ABC(SAS),
∴添加一个条件AB=CD(答案不唯一),使得△CDA≌△ABC.
故答案为:AB=CD(答案不唯一).
13.(2023秋 浦东新区期末)如图,DE垂直平分AB,FG垂直平分AC,若∠BAC=110°,则∠DAF= 40 度.
【解答】解:∵∠BAC=110°,
∴∠B+∠C=180°﹣∠BAC=180°﹣110°=70°,
∵DE垂直平分AB,
∴DA=DB,
∴∠DAB=∠B,
同理可得:∠PAC=∠C,
∴∠DAB+∠PAC=∠B+∠C=70°,
∴∠DAF=110°﹣70°=40°,
故答案为:40.
14.(2023秋 成都期末)在Rt△ABC中,∠BAC=90°,BD=AD=2,在BC的延长线上有一点E使得AE=AD,过点E作AC的垂线,垂足为F,若∠FEA=67.5°,则CE= 22 .
【解答】解:∵BD=AD,
∴∠B=∠BAD,
∴∠ADE=∠B+∠BAD=2∠B,
∵AD=AE,
∴∠AED=∠ADE=2∠B,
∵EF⊥AF,BA⊥AF,
∴EF∥AB,
∠CEF=∠B,
∴∠AEF=∠AEC+∠CEF=3∠B=67.5°,
∴∠B=22.5°,
∴∠ADE=45°,
∵∠AED=∠ADE=45°,
∴△ADE是等腰直角三角形,
∴DE2,
∵∠BAC=90°,
∴∠B+∠ACD=∠BAD+∠DAC=90°,
∴∠ACD=∠DAC,
∴DC=AD=2,
∴CE=DE﹣CD=22.
故答案为:22.
15.(2024春 南昌期末)在平面直角坐标系中,若点P(x,y)的坐标满足x﹣2y+3=0,则我们称点P为“健康点”;若点Q(x,y)的坐标满足x+y﹣6=0,则我们称点Q为“快乐点”,若点A既是“健康点”又是“快乐点”,则点A的坐标为 (3,3) ;
【解答】解:点A既是“健康点”又是“快乐点”,则A坐标应该满足x﹣2y+3=0和x+y﹣6=0,
解
得:,
∴A的坐标为(3,3);
故答案为:(3,3).
16.(2023秋 新城区校级期末)如图,在同一直角坐标系中,直线l1:y=3x+1与直线l2:y=mx+5相交于点A(1,n),则方程组的解为 .
【解答】解:∵直线l1:y=3x+1与直线l2:y=mx+5相交于点A(1,n),
∴n=3×1+1=4,
∴A(1,4),
∴方程组的解为.
故答案为:
17.(2023秋 忻州期末)生物活动小组的同学们观察某植物生长,得到该植物高度y(cm)与观察时间x(天)的关系,画出如图所示的函数图象(CD∥x轴),该植物最高长到 16cm .
【解答】解:设AC的函数关系式为y=kx+b(k、b为常数,且k≠0).
将A(0,6)和B(30,12)代入y=kx+b,
得,解得,
∴AC的函数关系式为yx+6(0≤x≤50).
当x=50时,yx+650+6=16,
∴该植物最高长到16cm.
故答案为:16cm.
三.解答题(共8小题)
18.(2023秋 广陵区校级期末)求值:
(1)计算:;
(2)已知:(x﹣1)2=4,求x的值.
【解答】解:(1)
;
(2)∵(x﹣1)2=4,
∴,
解得:x=3或x=﹣1.
19.(2023秋 桐城市校级期末)如图,网格中小正方形的边长为1,△ABC在平面直角坐标系中的位置如图所示.
(1)求△ABC的面积;
(2)作出△ABC关于x轴对称的△A′B′C′,并直接写出A′,B′,C′三点的坐标.
【解答】解:(1)依题意,
,
∴△ABC的面积为;
(2)如图:
∴A′,B′,C′三点的坐标分别是(4,﹣3),(3,﹣1),(1,﹣2),
20.(2023秋 常宁市期末)定义:如果一个三角形中有两个内角α,β满足α+2β=90°,那我们称这个三角形为“近直角三角形”.
(1)若△ABC是近直角三角形,∠B>90°,∠C=50°,则∠A= 20° .
(2)在Rt△ABC中,∠BAC=90°,AB=3,AC=4,若CD是∠ACB的平分线.
①求证:△BDC为近直角三角形.
②求BD的长.
【解答】解:(1)∠B不可能是α或β,
当∠A=α时,∠C=β=50°,α+2β=90°,不成立;
故∠A=β,∠C=α,α+2β=90°,则β=20°,
故答案为:20°;
(2)①如图1,设∠ACD=∠DCB=β,∠B=α,
则α+2β=90°,故△BDC是“近直角三角形”;
②如图2,过点D作DM⊥BC于点M,
∵CD平分∠ACB,DM⊥BC,DA⊥CA,
∴AD=DM.
在Rt△ACD和Rt△MCD中,
,
∴Rt△ACD≌Rt△MCD(HL).
∴AC=CM=4.
∵AB=3,AC=4,
∴BC5.
∴BM=1.
设AD=DM=x,
∵DM2+BM2=DB2,
∴x2+12=(3﹣x)2,
∴x,
∴BD=AB﹣AD=3.
21.(2023秋 隆昌市校级期末)如图,在△ABC中,AD平分∠BAC交BC于点D,CE⊥AD,分别交AB、AD于点E、F.
(1)求证:EF=CF;
(2)若∠ACB=80°,∠BCE=30°,求∠ABC的度数.
【解答】(1)证明:∵AD平分∠BAC,CE⊥AD,
∴∠EAF=∠CAF,∠AFE=∠AFC=90°,
在△AFE和△AFC中,
,
∴△AFE≌△AFC(ASA),
∴EF=CF;
(2)解:由(1)可得△AFE≌△AFC,
∴∠AEC=∠ACE,
∵∠ACB=80°,∠BCE=30°,
∴∠AEC=∠ACE=∠ACB﹣∠BCE=50°,
∴∠ABC=∠AEC﹣∠BCE=20°.
22.(2023秋 隆昌市校级期末)今年第6号台风“烟花”登录我国沿海地区,风力强,累计降雨量大,影响范围大,有极强的破坏力.如图,台风“烟花”中心沿东西方向AB由A向B移动,已知点C为一海港,且点C与直线AB上的两点A、B的距离分别为AC=600km,BC=800km,又AB=1000km,以台风中心为圆心,周围500km以内为受影响区域.
(1)求∠ACB的度数;
(2)经过查阅资料,小周同学发现若C到AB的距离大于500km,则海港C不受台风影响;若C到AB的距离小于或等于500km,则海港C会受台风影响,请你帮助小周同学计算C到AB的距离,判断海港C是否受台风影响?
【解答】解:(1)∵AC=600km,BC=800km,AB=1000km,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠ACB=90°;
(2)海港C受台风影响,理由如下:
过点C作CD⊥AB于点D,
∵△ABC是直角三角形,
∴AC BCCD AB,
∴CD480(km),
∵480km<500km,
∴海港C会受台风影响.
23.(2023秋 全椒县期末)如图,直线l1:y1=kx+a分别交x轴,y轴于点A(﹣2,0),B(0,1).直线l2:y2=﹣2x+b分别交x轴,y轴于点C,D,与直线l1相交于点E,已知OBOC.
(1)求直线l1的表达式;
(2)求y1>y2时,x的取值范围.
【解答】解:(1)根据题意得,
解得,
∴直线l1的表达式为y1x+1;
(2)∵B(0,1),
∴OB=1,
∵OBOC,
∴OC=3OB=3,
∴C(3,0),
把C(3,0)代入y2=﹣2x+b得﹣6+b=0,
解得b=6,
∴y2=﹣2x+6,
解不等式x+1>﹣2x+6得x>2,
即y1>y2时,x的取值范围为x>2.
24.(2023秋 金安区校级期末)某商场同时购进甲、乙两种商品共100件,其进价和售价如表:设其中甲种商品购进x件,商场售完这批商品的总利润为y元.
商品名称 甲 乙
进价(元/件) 40 90
售价(无/件) 60 120
(1)写出y关于x的函数关系式;
(2)该商品计划最多投入8000元用于购买这两种商品,则至少要购进多少件甲商品?若销售完这些商品,则商场可获得的最大利润是多少元?
【解答】解:(1)由题意得y=(60﹣40)x+(120﹣90)×(100﹣x)=﹣10x+3000,
∴y与x的函数关系式为y=﹣10x+3000.
(2)由题意得40x+90×(100﹣x)≤8000,
解得x≥20,
∵y=﹣10x+3000,
∴y随x的增大而减小,
∴当x=20时,利润最大且ymax=2800,
∴若售完这些商品,则至少购进20件甲商品商场可获得最大利润,获得的最大利润是2800元.
25.(2023秋 金台区期末)如图,直线y=2x+4与x轴交于点A,与y轴交于点B,点C是OB的中点.
(1)求点C的坐标;
(2)求△ABC的面积;
(3)在坐标轴上是否存在一点P,使得△ABP是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
【解答】解:(1)∵y=2x+4与y轴交于点B,
当x=0时,y=2×0+4=4,则B(0,4),
∴OB=4,
∵点C是OB的中点,
∴BC=OC=2,
∴C(0,2);
(2)当y=0时,2x+4=0,
∴x=﹣2,
∴OA=2,
∴S△ABCCB×AO2×2=2;
(3)分两种情况:
i)设x轴上存在一点P(m,0),使得△ABP是直角三角形,
∵A(﹣2,0),B(0,4),∠AOB=90°,
根据勾股定理可得:AB2=OB2+OA2,
∴AB2=42+22=20,
∵AP2=(m+2)2,BP2=m2+16,
△ABP是直角三角形,分两种情况:
①∠APB=90°时,P与原点重合,此时P(0,0);
②∠ABP=90°时,则AB2+BP2=AP2,
∴20+m2+16=(m+2)2,
解得:m=8,此时P(8,0);
ii)设y轴上存在一点P(0,n),使得△ABP是直角三角形,
∵AB2=20,BP2=(n﹣4)2,AP2=n2+4,
当∠BAP=90°时,则AB2+AP2=BP2,
∴20+4+n2=(n﹣4)2,
解得:n=﹣1,此时P(0,﹣1);
综上所述:P(0,0)或(8,0)或(0,﹣1).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
