期末真题重组卷-2024-2025学年数学八年级上册北师大版(含答案)
文档属性
| 名称 | 期末真题重组卷-2024-2025学年数学八年级上册北师大版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 692.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-15 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
期末真题重组卷-2024-2025学年数学八年级上册北师大版
一.选择题(共9小题)
1.(2023秋 榆树市期末)﹣8的立方根是( )
A.4 B.2 C.﹣2 D.±2
2.(2022秋 惠来县期末)已知一组数据8,5,x,8,10的平均数是8,以下说法错误的是( )
A.极差是5 B.众数是8 C.中位数是9 D.方差是2.8
3.(2024春 扶沟县期末)将下列长度的三根木棒首尾顺次连接,能组成直角三角形的是( )
A.1、2、3 B.2、3、4 C.3、4、5 D.4、5、6
4.(2023秋 罗湖区校级期末)下列各式中,是最简二次根式的是( )
A. B. C. D.
5.(2024春 会泽县期末)在平面直角坐标系中,点(3,﹣2)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.(2024春 田阳区期末)如图,在平面直角坐标系中,已知点A(﹣2,0),B(0,3),以点A为圆心,AB长为半径画弧,交x轴的正半轴于点C,则点C的横坐标为( )
A. B. C. D.
7.(2023秋 莲湖区期末)若一次函数y=(k﹣2)x+3的函数值y随自变量x的减小而增大,则k的取值范围是( )
A.k<2 B.k>2 C.k<0 D.k>3
8.(2023秋 尧都区校级期末)下列命题中,是真命题的是( )
A.三角形的一个外角大于任何一个内角
B.有且只有一条直线与已知直线垂直
C.0的平方根、算术平方根和立方根都是0
D.两边和一角对应相等的两个三角形全等
9.(2023秋 蜀山区期末)A,B两地相距640km,甲、乙两辆汽车从A地出发到B地,均匀速行驶,甲出发1小时后,乙出发沿同一路线行驶,设甲、乙两车相距s(km),甲行驶的时间为t(h),s与t的关系如图所示,下列说法:
①甲车行驶的速度是60km/h,乙车行驶的速度是80km/h;
②乙出发4h后追上甲;
③甲比乙晚到;
④甲车行驶8h或,甲,乙两车相距80km.
其中正确的是( )
A.①③ B.①②④ C.①③④ D.②③④
二.填空题(共7小题)
10.(2023秋 金台区期末)已知一个数的一个平方根是,则这个数是 .
11.(2023秋 金台区期末)若函数y=(4+m)x+|m|﹣4是正比例函数,则m的值是 .
12.(2023秋 金台区期末)如图所示,已知AB∥CD,AD和BC相交于点O,若∠A=42°,∠C=58°,则∠AOB= °.
13.(2023秋 兰州期末)在第二象限内的点P到x轴的距离是3,到y轴的距离是4,则点P的坐标是 .
14.(2023秋 金台区期末)如果实数x,y满足方程组,那么(2x+y)2023= .
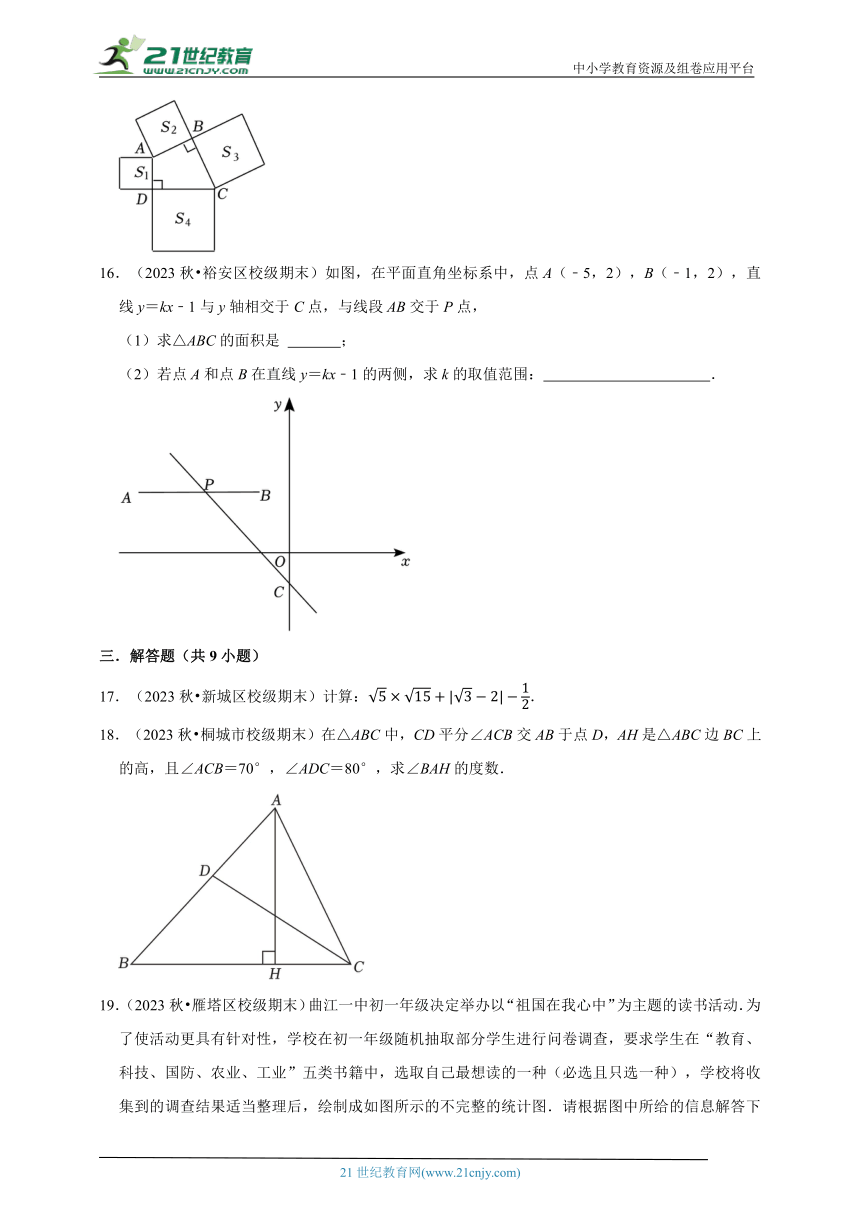
15.(2023秋 金台区期末)如图,在四边形ABCD中,∠ABC=∠CDA=90°,分别以四边形ABCD的四条边为边长,向外作四个正方形,面积分别为S1,S2,S3,S4,若S1=6,S2=12,S3=14,则S4的值为 .
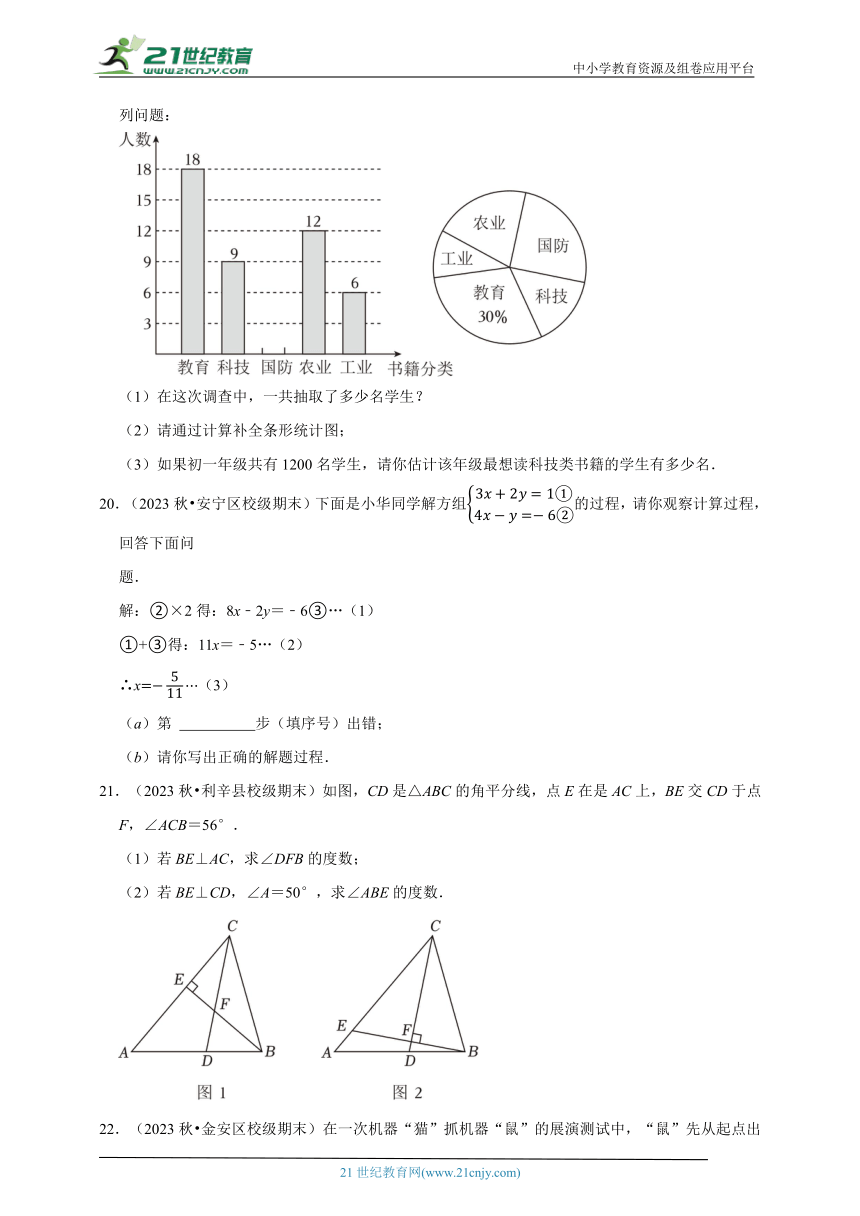
16.(2023秋 裕安区校级期末)如图,在平面直角坐标系中,点A(﹣5,2),B(﹣1,2),直线y=kx﹣1与y轴相交于C点,与线段AB交于P点,
(1)求△ABC的面积是 ;
(2)若点A和点B在直线y=kx﹣1的两侧,求k的取值范围: .
三.解答题(共9小题)
17.(2023秋 新城区校级期末)计算:.
18.(2023秋 桐城市校级期末)在△ABC中,CD平分∠ACB交AB于点D,AH是△ABC边BC上的高,且∠ACB=70°,∠ADC=80°,求∠BAH的度数.
19.(2023秋 雁塔区校级期末)曲江一中初一年级决定举办以“祖国在我心中”为主题的读书活动.为了使活动更具有针对性,学校在初一年级随机抽取部分学生进行问卷调查,要求学生在“教育、科技、国防、农业、工业”五类书籍中,选取自己最想读的一种(必选且只选一种),学校将收集到的调查结果适当整理后,绘制成如图所示的不完整的统计图.请根据图中所给的信息解答下列问题:
(1)在这次调查中,一共抽取了多少名学生?
(2)请通过计算补全条形统计图;
(3)如果初一年级共有1200名学生,请你估计该年级最想读科技类书籍的学生有多少名.
20.(2023秋 安宁区校级期末)下面是小华同学解方组的过程,请你观察计算过程,回答下面问
题.
解:②×2得:8x﹣2y=﹣6③…(1)
①+③得:11x=﹣5…(2)
∴x(3)
(a)第 步(填序号)出错;
(b)请你写出正确的解题过程.
21.(2023秋 利辛县校级期末)如图,CD是△ABC的角平分线,点E在是AC上,BE交CD于点F,∠ACB=56°.
(1)若BE⊥AC,求∠DFB的度数;
(2)若BE⊥CD,∠A=50°,求∠ABE的度数.
22.(2023秋 金安区校级期末)在一次机器“猫”抓机器“鼠”的展演测试中,“鼠”先从起点出发,1min后,“猫”从同起点出发去追“鼠”,抓住“鼠”并稍作停留后,“猫”抓着“鼠”沿原路返回.“鼠”、“猫距起点的距离y(m)与时间x(min)之间的关系如图所示.
(1)在“猫”追“鼠”的过程中,“鼠”的平均速度是 m/min;
(2)求AB所在直线的函数表达式;
(3)求“猫”从起点出发到返回至起点所用的时间.
23.(2023秋 安宁区校级期末)如图,直线y1=2x﹣2的图象与y轴交于点A,直线y2=﹣2x+6的图象与y轴交于点B,两者相交于点C.
(1)方程组的解是 ;
(2)当y1>0与y2>0同时成立时,x的取值范围为 ;
(3)求△ABC的面积.
24.(2023秋 桐城市校级期末)某公司销售A型和B型两种电脑,其中A型电脑每台利润为400元,B型电脑每台利润为500元.该公司计划一次性购进这两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
(1)求y关于x的函数关系式;
(2)该商店购进A型、B型电脑各多少台,才能使销售总利润最大,最大利润是多少?
(3)实际进货时,厂家对A型电脑出厂价下调a(0<a<200)元,若该公司保持这两种型号电脑的售价不变,并且无论该公司如何进货这100台电脑的销售利润不变,求a的值.
25.(2023秋 台江区期末)在数学实践活动课上,小亮同学利用一副三角尺探索与研究共直角顶点的两个直角三角形中的位置关系与数量关系.(其中∠A=30°,∠B=60°,∠C=∠D=45°)
(1)将三角尺如图1所示叠放在一起.
①∠AOD与∠BOC大小关系是 ;
②∠BOD与∠AOC的数量关系是 .
(2)小亮固定其中一块三角尺△COD不变,绕点O顺时针转动另一块三角尺,从图2的OA与OC重合开始,到图3的OA与OC在一条直线上时结束,探索△AOB的一边与△COD的一边平行的情况.
①求当AB∥CD时,如图4所示,∠AOC的大小;
②直接写出∠AOC的其余所有可能值.
期末真题重组卷-2024-2025学年数学八年级上册北师大版
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9
答案 C C C C D A A C C
一.选择题(共9小题)
1.(2023秋 榆树市期末)﹣8的立方根是( )
A.4 B.2 C.﹣2 D.±2
【解答】解:﹣8的立方根是﹣2.
故选:C.
2.(2022秋 惠来县期末)已知一组数据8,5,x,8,10的平均数是8,以下说法错误的是( )
A.极差是5 B.众数是8 C.中位数是9 D.方差是2.8
【解答】解:∵一组数据8,5,x,8,10的平均数是8,
∴(8+5+x+8+10)=8,
解得x=9,
∴这组数据为:5,8,8,9,10,
∴极差为10﹣5=5,A正确;
众数是8,B正确;
中位数是8,故C错误;
方差为:[(5﹣8)2+(8﹣8)2+(8﹣8)2+(9﹣8)2+(10﹣8)2]=2.8,故D正确.
故选:C.
3.(2024春 扶沟县期末)将下列长度的三根木棒首尾顺次连接,能组成直角三角形的是( )
A.1、2、3 B.2、3、4 C.3、4、5 D.4、5、6
【解答】解:A、∵12+22≠32,∴不能组成直角三角形,故A选项错误;
B、∵22+32≠42,∴不能组成直角三角形,故B选项错误;
C、∵32+42=52,∴组成直角三角形,故C选项正确;
D、∵42+52≠62,∴不能组成直角三角形,故D选项错误.
故选:C.
4.(2023秋 罗湖区校级期末)下列各式中,是最简二次根式的是( )
A. B. C. D.
【解答】解:A、,则A选项错误,不符合题意;
B、,则B选项错误,不符合题意;
C、是最简二次根式,正确,故符合题意;
D、,则D选项错误,不符合题意.
故选:C.
5.(2024春 会泽县期末)在平面直角坐标系中,点(3,﹣2)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【解答】解:点(3,﹣2)所在象限是第四象限.
故选:D.
6.(2024春 田阳区期末)如图,在平面直角坐标系中,已知点A(﹣2,0),B(0,3),以点A为圆心,AB长为半径画弧,交x轴的正半轴于点C,则点C的横坐标为( )
A. B. C. D.
【解答】解:根据题意,可知,AC=AB,
∴.
又点A的坐标为(﹣2,0),
∴点C的坐标为.
故选:A.
7.(2023秋 莲湖区期末)若一次函数y=(k﹣2)x+3的函数值y随自变量x的减小而增大,则k的取值范围是( )
A.k<2 B.k>2 C.k<0 D.k>3
【解答】解:∵一次函数y=(k﹣2)x+3的函数值y随自变量x的减小而增大,
∴k﹣2<0,解得:k<2,
故选:A.
8.(2023秋 尧都区校级期末)下列命题中,是真命题的是( )
A.三角形的一个外角大于任何一个内角
B.有且只有一条直线与已知直线垂直
C.0的平方根、算术平方根和立方根都是0
D.两边和一角对应相等的两个三角形全等
【解答】解:A.三角形一个外角大于它不相邻的任何一个内角,故此命题是假命题,不符合题意;
B.同一平面内,过一点有且只有一条直线与已知直线垂直,故此命题是假命题,不符合题意;
C.0的平方根、算术平方根和立方根都是0,故此命题为真命题,符合题意;
D.两边对应相等,且两边的夹角相等,则这两个三角形全等,故此命题是假命题,不符合题意.
故选:C.
9.(2023秋 蜀山区期末)A,B两地相距640km,甲、乙两辆汽车从A地出发到B地,均匀速行驶,甲出发1小时后,乙出发沿同一路线行驶,设甲、乙两车相距s(km),甲行驶的时间为t(h),s与t的关系如图所示,下列说法:
①甲车行驶的速度是60km/h,乙车行驶的速度是80km/h;
②乙出发4h后追上甲;
③甲比乙晚到;
④甲车行驶8h或,甲,乙两车相距80km.
其中正确的是( )
A.①③ B.①②④ C.①③④ D.②③④
【解答】解:①由图可得,甲车行驶的速度是60÷1=60km/h,
∵甲先出发1h,乙出发3h后追上甲,
∴3(v乙﹣60)=60,
∴v乙=80km/h,
即乙车行驶的速度是80km/h,故①正确;
②∵当t=1时,乙出发,当t=4时,乙追上甲,
∴乙出发3h后追上甲,故②错误;
③由图可得,当乙到达B地时,甲乙相距100km,
∴甲比乙晚到,故③正确;
④由图可得,当乙车在甲车前,且未到达B地时,则60t+80=80(t﹣1),
解得t=8;
当乙车到达B地后时,60t+80=640,
解得,
∴甲车行驶8h或,甲,乙两车相距80km,故④正确;
综上所述,①③④正确.
故选:C.
二.填空题(共7小题)
10.(2023秋 金台区期末)已知一个数的一个平方根是,则这个数是 6 .
【解答】解:∵一个数的一个平方根是,
∴这个数是()2=6.
故答案为:6.
11.(2023秋 金台区期末)若函数y=(4+m)x+|m|﹣4是正比例函数,则m的值是 4 .
【解答】解:由题意知,4+m≠0且|m|﹣4=0,
解得m=4,
故答案为:4.
12.(2023秋 金台区期末)如图所示,已知AB∥CD,AD和BC相交于点O,若∠A=42°,∠C=58°,则∠AOB= 80 °.
【解答】解:∵AB平行CD,
∴∠B=∠C=58°,
在△ABO中,∠AOB+∠A+∠B=180°
∴∠AOB=180°﹣58°﹣42°=80°.
故答案为:80°.
13.(2023秋 兰州期末)在第二象限内的点P到x轴的距离是3,到y轴的距离是4,则点P的坐标是 (﹣4,3) .
【解答】解:第二象限内的点横坐标小于0,纵坐标大于0;到x轴的距离是3,说明点的纵坐标为3,到y轴的距离为4,说明点的横坐标为﹣4,因而点P的坐标是(﹣4,3).故答案填:(﹣4,3).
14.(2023秋 金台区期末)如果实数x,y满足方程组,那么(2x+y)2023= ﹣1 .
【解答】解:将x+2y=﹣2记作①,x﹣y=1记作②,
①+②,得2x+y=﹣1,
∴(2x+y)2023=(﹣1)2023=﹣1.
故答案为:﹣1.
15.(2023秋 金台区期末)如图,在四边形ABCD中,∠ABC=∠CDA=90°,分别以四边形ABCD的四条边为边长,向外作四个正方形,面积分别为S1,S2,S3,S4,若S1=6,S2=12,S3=14,则S4的值为 20 .
【解答】解:如图,连接AC,
∵S1=6,S2=12,S3=14,
∴AD2=6,AB2=12,BC2=14,
在Rt△ABC与Rt△ADC中,由勾股定理得,
AC2=AB2+BC2=26,
CD2=AC2﹣AD2,
∴CD2=26﹣6=20,
∴S4=20,
故答案为:20.
16.(2023秋 裕安区校级期末)如图,在平面直角坐标系中,点A(﹣5,2),B(﹣1,2),直线y=kx﹣1与y轴相交于C点,与线段AB交于P点,
(1)求△ABC的面积是 6 ;
(2)若点A和点B在直线y=kx﹣1的两侧,求k的取值范围: .
【解答】解:(1)∵A(﹣5,2),B(﹣1,2),
∴AB∥x轴,延长线段AB交y轴于点D,AB⊥y轴,
∵CD=2﹣(﹣1)=3,AB=﹣1﹣(﹣5)=4,
∴,
故答案为:6;
(2)设直线AC的解析式为y=kx+b(k≠0),
∴,
解得,
∴直线AC的解析式为,
设直线BC的解析式为y=mx+n(m≠0),
∴,
解得,
∴直线BC的解析式为y=﹣3x﹣1,
∵点A和点B在直线y=kx﹣1的两侧,
∴
故答案为:.
三.解答题(共9小题)
17.(2023秋 新城区校级期末)计算:.
【解答】解:
.
18.(2023秋 桐城市校级期末)在△ABC中,CD平分∠ACB交AB于点D,AH是△ABC边BC上的高,且∠ACB=70°,∠ADC=80°,求∠BAH的度数.
【解答】解:∵CD平分∠ACB,∠ACB=70°,
∴∠ACD∠ACB=35°,
∵∠ADC=80°,
∴∠BAC=180°﹣∠ACD﹣∠ADC=180°﹣35°﹣80°=65°;
∵AH⊥BC,
∴∠AHC=90°,
∴∠HAC=90°﹣∠ACB=90°﹣70°=20°,
∴∠BAH=∠BAC﹣∠HAC=65°﹣20°=45°.
19.(2023秋 雁塔区校级期末)曲江一中初一年级决定举办以“祖国在我心中”为主题的读书活动.为了使活动更具有针对性,学校在初一年级随机抽取部分学生进行问卷调查,要求学生在“教育、科技、国防、农业、工业”五类书籍中,选取自己最想读的一种(必选且只选一种),学校将收集到的调查结果适当整理后,绘制成如图所示的不完整的统计图.请根据图中所给的信息解答下列问题:
(1)在这次调查中,一共抽取了多少名学生?
(2)请通过计算补全条形统计图;
(3)如果初一年级共有1200名学生,请你估计该年级最想读科技类书籍的学生有多少名.
【解答】解:(1)由题意知,一共抽取了(名)学生,
∴一共抽取了60名学生;
(2)由题意知,国防的人数为60﹣18﹣9﹣12﹣6=15(人),
补图如下:
(3)由题意知,(名),
∴估计该年级最想读科技类书籍的学生有180名.
20.(2023秋 安宁区校级期末)下面是小华同学解方组的过程,请你观察计算过程,回答下面问
题.
解:②×2得:8x﹣2y=﹣6③…(1)
①+③得:11x=﹣5…(2)
∴x(3)
(a)第 (1) 步(填序号)出错;
(b)请你写出正确的解题过程.
【解答】解:(a)第(1)步出错,
故答案为:(1);
(b),
②×2得:8x﹣2y=﹣12③,
①+③得:11x=﹣11,
∴x=﹣1,
把x=﹣1代入②,得y=2,
所以方程组的解是.
21.(2023秋 利辛县校级期末)如图,CD是△ABC的角平分线,点E在是AC上,BE交CD于点F,∠ACB=56°.
(1)若BE⊥AC,求∠DFB的度数;
(2)若BE⊥CD,∠A=50°,求∠ABE的度数.
【解答】解:(1)∵CD是∠ACB的平分线,
∴,
∵BE⊥AC,
∴∠CEF=90°.
∴∠EFC=90°﹣∠ACD=62°,
∴∠DFB=∠EFC=62°;
(2)∵BE⊥CD,CD是∠ACB 的平分线,
∴∠CFE=90°,∠ACD=28°,
∴∠CEB=180°﹣∠CFE﹣∠ACD=62°,
∴∠AEB=180°﹣∠CEB=118°,
∴∠ABE=180°﹣∠AEB﹣∠A=180°﹣118°﹣50°=12°.
22.(2023秋 金安区校级期末)在一次机器“猫”抓机器“鼠”的展演测试中,“鼠”先从起点出发,1min后,“猫”从同起点出发去追“鼠”,抓住“鼠”并稍作停留后,“猫”抓着“鼠”沿原路返回.“鼠”、“猫距起点的距离y(m)与时间x(min)之间的关系如图所示.
(1)在“猫”追“鼠”的过程中,“鼠”的平均速度是 5 m/min;
(2)求AB所在直线的函数表达式;
(3)求“猫”从起点出发到返回至起点所用的时间.
【解答】解:(1)由图象知:“鼠”6min跑了30m,
∴“鼠”的速度为:30÷6=5(m/min),
∴“鼠”的平均速度为5m/min;
(2)设AB的解析式为:y=kx+b,
∵图象经过A(7,30)和B(10,18),
把点A和点B坐标代入函数解析式得:
,
解得:,
∴AB的解析式为:y=﹣4x+58;
(3)令y=0,则﹣4x+58=0,
∴x=14.5,
∵“猫”比“鼠”迟一分钟出发,
∴“猫”从起点出发到返回至起点所用的时间为14.5﹣1=13.5(min).
答:“猫”从起点出发到返回至起点所用的时间为13.5min.
23.(2023秋 安宁区校级期末)如图,直线y1=2x﹣2的图象与y轴交于点A,直线y2=﹣2x+6的图象与y轴交于点B,两者相交于点C.
(1)方程组的解是 ;
(2)当y1>0与y2>0同时成立时,x的取值范围为 1<x<3 ;
(3)求△ABC的面积.
【解答】解:(1)如图所示:方程组组的解为:;
故答案为:;
(2)如图所示:当y1>0与y2>0同时成立时,
x取何值范围是:1<x<3;
故答案为:1<x<3;
(3)∵令x=0,则y1=﹣2,y2=6,
∴A(0,﹣2),B(0,6).
∴AB=8.
∴S△ABC8×2=8.
24.(2023秋 桐城市校级期末)某公司销售A型和B型两种电脑,其中A型电脑每台利润为400元,B型电脑每台利润为500元.该公司计划一次性购进这两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
(1)求y关于x的函数关系式;
(2)该商店购进A型、B型电脑各多少台,才能使销售总利润最大,最大利润是多少?
(3)实际进货时,厂家对A型电脑出厂价下调a(0<a<200)元,若该公司保持这两种型号电脑的售价不变,并且无论该公司如何进货这100台电脑的销售利润不变,求a的值.
【解答】解:(1)根据题意,y=400x+500(100﹣x)=﹣100x+50000;
(2)∵100﹣x≤2x,
∴x,
∵y=﹣100x+50000中k=﹣100<0,
∴y随x的增大而减小,
∵x为整数,
∴x=34时,y取得最大值,最大值为46600,
答:该商店购进A型34台、B型电脑66台,才能使销售总利润最大,最大利润是46600元;
(3)据题意得,y=(400+a)x+500(100﹣x),即y=(a﹣100)x+50000,
当a=100时,无论该公司如何进货这100台电脑的销售利润不变.
25.(2023秋 台江区期末)在数学实践活动课上,小亮同学利用一副三角尺探索与研究共直角顶点的两个直角三角形中的位置关系与数量关系.(其中∠A=30°,∠B=60°,∠C=∠D=45°)
(1)将三角尺如图1所示叠放在一起.
①∠AOD与∠BOC大小关系是 相等 ;
②∠BOD与∠AOC的数量关系是 ∠BOD+∠AOC=180° .
(2)小亮固定其中一块三角尺△COD不变,绕点O顺时针转动另一块三角尺,从图2的OA与OC重合开始,到图3的OA与OC在一条直线上时结束,探索△AOB的一边与△COD的一边平行的情况.
①求当AB∥CD时,如图4所示,∠AOC的大小;
②直接写出∠AOC的其余所有可能值.
【解答】解:(1)①∠AOD与∠BOC大小关系是相等;
∵∠AOD+∠AOC=90°,∠BOC+∠AOC=90°,
∴∠AOD=∠BOC,
故答案为:相等;
②∠BOD与∠AOC的数量关系是:∠BOD+∠AOC=180°;
∵∠DOC=90°,∠AOB=∠BOC+∠AOC=90°,
∴∠BOD+∠AOC=∠COD+∠COB+∠AOC=180°;
(2)①过点O作OE∥AB,如图4.1,
∵AB∥CD,
∴AB∥CD∥OE,
∴∠AOE=∠A=30°,∠COE=∠C=45°,
∴∠AOC=∠AOE+∠COE=75°;
②当AB∥OC时,如图4.2,则∠AOC=∠A=30°;
当OA∥CD时,如图4.3,则∠AOC=∠C=45°;
当AB∥OD时,如图4.4,则∠BOD=∠B=60°,
∴∠AOC=360°﹣90°﹣90°﹣∠BOD=120°;
当OB∥CD时,如图4.5,则∠BOD=∠D=45°,
∴∠AOC=360°﹣90°﹣90°﹣∠BOD=135°;
综上所述:∠AOC的其余可能值为30°或45°或120°或135°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末真题重组卷-2024-2025学年数学八年级上册北师大版
一.选择题(共9小题)
1.(2023秋 榆树市期末)﹣8的立方根是( )
A.4 B.2 C.﹣2 D.±2
2.(2022秋 惠来县期末)已知一组数据8,5,x,8,10的平均数是8,以下说法错误的是( )
A.极差是5 B.众数是8 C.中位数是9 D.方差是2.8
3.(2024春 扶沟县期末)将下列长度的三根木棒首尾顺次连接,能组成直角三角形的是( )
A.1、2、3 B.2、3、4 C.3、4、5 D.4、5、6
4.(2023秋 罗湖区校级期末)下列各式中,是最简二次根式的是( )
A. B. C. D.
5.(2024春 会泽县期末)在平面直角坐标系中,点(3,﹣2)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.(2024春 田阳区期末)如图,在平面直角坐标系中,已知点A(﹣2,0),B(0,3),以点A为圆心,AB长为半径画弧,交x轴的正半轴于点C,则点C的横坐标为( )
A. B. C. D.
7.(2023秋 莲湖区期末)若一次函数y=(k﹣2)x+3的函数值y随自变量x的减小而增大,则k的取值范围是( )
A.k<2 B.k>2 C.k<0 D.k>3
8.(2023秋 尧都区校级期末)下列命题中,是真命题的是( )
A.三角形的一个外角大于任何一个内角
B.有且只有一条直线与已知直线垂直
C.0的平方根、算术平方根和立方根都是0
D.两边和一角对应相等的两个三角形全等
9.(2023秋 蜀山区期末)A,B两地相距640km,甲、乙两辆汽车从A地出发到B地,均匀速行驶,甲出发1小时后,乙出发沿同一路线行驶,设甲、乙两车相距s(km),甲行驶的时间为t(h),s与t的关系如图所示,下列说法:
①甲车行驶的速度是60km/h,乙车行驶的速度是80km/h;
②乙出发4h后追上甲;
③甲比乙晚到;
④甲车行驶8h或,甲,乙两车相距80km.
其中正确的是( )
A.①③ B.①②④ C.①③④ D.②③④
二.填空题(共7小题)
10.(2023秋 金台区期末)已知一个数的一个平方根是,则这个数是 .
11.(2023秋 金台区期末)若函数y=(4+m)x+|m|﹣4是正比例函数,则m的值是 .
12.(2023秋 金台区期末)如图所示,已知AB∥CD,AD和BC相交于点O,若∠A=42°,∠C=58°,则∠AOB= °.
13.(2023秋 兰州期末)在第二象限内的点P到x轴的距离是3,到y轴的距离是4,则点P的坐标是 .
14.(2023秋 金台区期末)如果实数x,y满足方程组,那么(2x+y)2023= .
15.(2023秋 金台区期末)如图,在四边形ABCD中,∠ABC=∠CDA=90°,分别以四边形ABCD的四条边为边长,向外作四个正方形,面积分别为S1,S2,S3,S4,若S1=6,S2=12,S3=14,则S4的值为 .
16.(2023秋 裕安区校级期末)如图,在平面直角坐标系中,点A(﹣5,2),B(﹣1,2),直线y=kx﹣1与y轴相交于C点,与线段AB交于P点,
(1)求△ABC的面积是 ;
(2)若点A和点B在直线y=kx﹣1的两侧,求k的取值范围: .
三.解答题(共9小题)
17.(2023秋 新城区校级期末)计算:.
18.(2023秋 桐城市校级期末)在△ABC中,CD平分∠ACB交AB于点D,AH是△ABC边BC上的高,且∠ACB=70°,∠ADC=80°,求∠BAH的度数.
19.(2023秋 雁塔区校级期末)曲江一中初一年级决定举办以“祖国在我心中”为主题的读书活动.为了使活动更具有针对性,学校在初一年级随机抽取部分学生进行问卷调查,要求学生在“教育、科技、国防、农业、工业”五类书籍中,选取自己最想读的一种(必选且只选一种),学校将收集到的调查结果适当整理后,绘制成如图所示的不完整的统计图.请根据图中所给的信息解答下列问题:
(1)在这次调查中,一共抽取了多少名学生?
(2)请通过计算补全条形统计图;
(3)如果初一年级共有1200名学生,请你估计该年级最想读科技类书籍的学生有多少名.
20.(2023秋 安宁区校级期末)下面是小华同学解方组的过程,请你观察计算过程,回答下面问
题.
解:②×2得:8x﹣2y=﹣6③…(1)
①+③得:11x=﹣5…(2)
∴x(3)
(a)第 步(填序号)出错;
(b)请你写出正确的解题过程.
21.(2023秋 利辛县校级期末)如图,CD是△ABC的角平分线,点E在是AC上,BE交CD于点F,∠ACB=56°.
(1)若BE⊥AC,求∠DFB的度数;
(2)若BE⊥CD,∠A=50°,求∠ABE的度数.
22.(2023秋 金安区校级期末)在一次机器“猫”抓机器“鼠”的展演测试中,“鼠”先从起点出发,1min后,“猫”从同起点出发去追“鼠”,抓住“鼠”并稍作停留后,“猫”抓着“鼠”沿原路返回.“鼠”、“猫距起点的距离y(m)与时间x(min)之间的关系如图所示.
(1)在“猫”追“鼠”的过程中,“鼠”的平均速度是 m/min;
(2)求AB所在直线的函数表达式;
(3)求“猫”从起点出发到返回至起点所用的时间.
23.(2023秋 安宁区校级期末)如图,直线y1=2x﹣2的图象与y轴交于点A,直线y2=﹣2x+6的图象与y轴交于点B,两者相交于点C.
(1)方程组的解是 ;
(2)当y1>0与y2>0同时成立时,x的取值范围为 ;
(3)求△ABC的面积.
24.(2023秋 桐城市校级期末)某公司销售A型和B型两种电脑,其中A型电脑每台利润为400元,B型电脑每台利润为500元.该公司计划一次性购进这两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
(1)求y关于x的函数关系式;
(2)该商店购进A型、B型电脑各多少台,才能使销售总利润最大,最大利润是多少?
(3)实际进货时,厂家对A型电脑出厂价下调a(0<a<200)元,若该公司保持这两种型号电脑的售价不变,并且无论该公司如何进货这100台电脑的销售利润不变,求a的值.
25.(2023秋 台江区期末)在数学实践活动课上,小亮同学利用一副三角尺探索与研究共直角顶点的两个直角三角形中的位置关系与数量关系.(其中∠A=30°,∠B=60°,∠C=∠D=45°)
(1)将三角尺如图1所示叠放在一起.
①∠AOD与∠BOC大小关系是 ;
②∠BOD与∠AOC的数量关系是 .
(2)小亮固定其中一块三角尺△COD不变,绕点O顺时针转动另一块三角尺,从图2的OA与OC重合开始,到图3的OA与OC在一条直线上时结束,探索△AOB的一边与△COD的一边平行的情况.
①求当AB∥CD时,如图4所示,∠AOC的大小;
②直接写出∠AOC的其余所有可能值.
期末真题重组卷-2024-2025学年数学八年级上册北师大版
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9
答案 C C C C D A A C C
一.选择题(共9小题)
1.(2023秋 榆树市期末)﹣8的立方根是( )
A.4 B.2 C.﹣2 D.±2
【解答】解:﹣8的立方根是﹣2.
故选:C.
2.(2022秋 惠来县期末)已知一组数据8,5,x,8,10的平均数是8,以下说法错误的是( )
A.极差是5 B.众数是8 C.中位数是9 D.方差是2.8
【解答】解:∵一组数据8,5,x,8,10的平均数是8,
∴(8+5+x+8+10)=8,
解得x=9,
∴这组数据为:5,8,8,9,10,
∴极差为10﹣5=5,A正确;
众数是8,B正确;
中位数是8,故C错误;
方差为:[(5﹣8)2+(8﹣8)2+(8﹣8)2+(9﹣8)2+(10﹣8)2]=2.8,故D正确.
故选:C.
3.(2024春 扶沟县期末)将下列长度的三根木棒首尾顺次连接,能组成直角三角形的是( )
A.1、2、3 B.2、3、4 C.3、4、5 D.4、5、6
【解答】解:A、∵12+22≠32,∴不能组成直角三角形,故A选项错误;
B、∵22+32≠42,∴不能组成直角三角形,故B选项错误;
C、∵32+42=52,∴组成直角三角形,故C选项正确;
D、∵42+52≠62,∴不能组成直角三角形,故D选项错误.
故选:C.
4.(2023秋 罗湖区校级期末)下列各式中,是最简二次根式的是( )
A. B. C. D.
【解答】解:A、,则A选项错误,不符合题意;
B、,则B选项错误,不符合题意;
C、是最简二次根式,正确,故符合题意;
D、,则D选项错误,不符合题意.
故选:C.
5.(2024春 会泽县期末)在平面直角坐标系中,点(3,﹣2)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【解答】解:点(3,﹣2)所在象限是第四象限.
故选:D.
6.(2024春 田阳区期末)如图,在平面直角坐标系中,已知点A(﹣2,0),B(0,3),以点A为圆心,AB长为半径画弧,交x轴的正半轴于点C,则点C的横坐标为( )
A. B. C. D.
【解答】解:根据题意,可知,AC=AB,
∴.
又点A的坐标为(﹣2,0),
∴点C的坐标为.
故选:A.
7.(2023秋 莲湖区期末)若一次函数y=(k﹣2)x+3的函数值y随自变量x的减小而增大,则k的取值范围是( )
A.k<2 B.k>2 C.k<0 D.k>3
【解答】解:∵一次函数y=(k﹣2)x+3的函数值y随自变量x的减小而增大,
∴k﹣2<0,解得:k<2,
故选:A.
8.(2023秋 尧都区校级期末)下列命题中,是真命题的是( )
A.三角形的一个外角大于任何一个内角
B.有且只有一条直线与已知直线垂直
C.0的平方根、算术平方根和立方根都是0
D.两边和一角对应相等的两个三角形全等
【解答】解:A.三角形一个外角大于它不相邻的任何一个内角,故此命题是假命题,不符合题意;
B.同一平面内,过一点有且只有一条直线与已知直线垂直,故此命题是假命题,不符合题意;
C.0的平方根、算术平方根和立方根都是0,故此命题为真命题,符合题意;
D.两边对应相等,且两边的夹角相等,则这两个三角形全等,故此命题是假命题,不符合题意.
故选:C.
9.(2023秋 蜀山区期末)A,B两地相距640km,甲、乙两辆汽车从A地出发到B地,均匀速行驶,甲出发1小时后,乙出发沿同一路线行驶,设甲、乙两车相距s(km),甲行驶的时间为t(h),s与t的关系如图所示,下列说法:
①甲车行驶的速度是60km/h,乙车行驶的速度是80km/h;
②乙出发4h后追上甲;
③甲比乙晚到;
④甲车行驶8h或,甲,乙两车相距80km.
其中正确的是( )
A.①③ B.①②④ C.①③④ D.②③④
【解答】解:①由图可得,甲车行驶的速度是60÷1=60km/h,
∵甲先出发1h,乙出发3h后追上甲,
∴3(v乙﹣60)=60,
∴v乙=80km/h,
即乙车行驶的速度是80km/h,故①正确;
②∵当t=1时,乙出发,当t=4时,乙追上甲,
∴乙出发3h后追上甲,故②错误;
③由图可得,当乙到达B地时,甲乙相距100km,
∴甲比乙晚到,故③正确;
④由图可得,当乙车在甲车前,且未到达B地时,则60t+80=80(t﹣1),
解得t=8;
当乙车到达B地后时,60t+80=640,
解得,
∴甲车行驶8h或,甲,乙两车相距80km,故④正确;
综上所述,①③④正确.
故选:C.
二.填空题(共7小题)
10.(2023秋 金台区期末)已知一个数的一个平方根是,则这个数是 6 .
【解答】解:∵一个数的一个平方根是,
∴这个数是()2=6.
故答案为:6.
11.(2023秋 金台区期末)若函数y=(4+m)x+|m|﹣4是正比例函数,则m的值是 4 .
【解答】解:由题意知,4+m≠0且|m|﹣4=0,
解得m=4,
故答案为:4.
12.(2023秋 金台区期末)如图所示,已知AB∥CD,AD和BC相交于点O,若∠A=42°,∠C=58°,则∠AOB= 80 °.
【解答】解:∵AB平行CD,
∴∠B=∠C=58°,
在△ABO中,∠AOB+∠A+∠B=180°
∴∠AOB=180°﹣58°﹣42°=80°.
故答案为:80°.
13.(2023秋 兰州期末)在第二象限内的点P到x轴的距离是3,到y轴的距离是4,则点P的坐标是 (﹣4,3) .
【解答】解:第二象限内的点横坐标小于0,纵坐标大于0;到x轴的距离是3,说明点的纵坐标为3,到y轴的距离为4,说明点的横坐标为﹣4,因而点P的坐标是(﹣4,3).故答案填:(﹣4,3).
14.(2023秋 金台区期末)如果实数x,y满足方程组,那么(2x+y)2023= ﹣1 .
【解答】解:将x+2y=﹣2记作①,x﹣y=1记作②,
①+②,得2x+y=﹣1,
∴(2x+y)2023=(﹣1)2023=﹣1.
故答案为:﹣1.
15.(2023秋 金台区期末)如图,在四边形ABCD中,∠ABC=∠CDA=90°,分别以四边形ABCD的四条边为边长,向外作四个正方形,面积分别为S1,S2,S3,S4,若S1=6,S2=12,S3=14,则S4的值为 20 .
【解答】解:如图,连接AC,
∵S1=6,S2=12,S3=14,
∴AD2=6,AB2=12,BC2=14,
在Rt△ABC与Rt△ADC中,由勾股定理得,
AC2=AB2+BC2=26,
CD2=AC2﹣AD2,
∴CD2=26﹣6=20,
∴S4=20,
故答案为:20.
16.(2023秋 裕安区校级期末)如图,在平面直角坐标系中,点A(﹣5,2),B(﹣1,2),直线y=kx﹣1与y轴相交于C点,与线段AB交于P点,
(1)求△ABC的面积是 6 ;
(2)若点A和点B在直线y=kx﹣1的两侧,求k的取值范围: .
【解答】解:(1)∵A(﹣5,2),B(﹣1,2),
∴AB∥x轴,延长线段AB交y轴于点D,AB⊥y轴,
∵CD=2﹣(﹣1)=3,AB=﹣1﹣(﹣5)=4,
∴,
故答案为:6;
(2)设直线AC的解析式为y=kx+b(k≠0),
∴,
解得,
∴直线AC的解析式为,
设直线BC的解析式为y=mx+n(m≠0),
∴,
解得,
∴直线BC的解析式为y=﹣3x﹣1,
∵点A和点B在直线y=kx﹣1的两侧,
∴
故答案为:.
三.解答题(共9小题)
17.(2023秋 新城区校级期末)计算:.
【解答】解:
.
18.(2023秋 桐城市校级期末)在△ABC中,CD平分∠ACB交AB于点D,AH是△ABC边BC上的高,且∠ACB=70°,∠ADC=80°,求∠BAH的度数.
【解答】解:∵CD平分∠ACB,∠ACB=70°,
∴∠ACD∠ACB=35°,
∵∠ADC=80°,
∴∠BAC=180°﹣∠ACD﹣∠ADC=180°﹣35°﹣80°=65°;
∵AH⊥BC,
∴∠AHC=90°,
∴∠HAC=90°﹣∠ACB=90°﹣70°=20°,
∴∠BAH=∠BAC﹣∠HAC=65°﹣20°=45°.
19.(2023秋 雁塔区校级期末)曲江一中初一年级决定举办以“祖国在我心中”为主题的读书活动.为了使活动更具有针对性,学校在初一年级随机抽取部分学生进行问卷调查,要求学生在“教育、科技、国防、农业、工业”五类书籍中,选取自己最想读的一种(必选且只选一种),学校将收集到的调查结果适当整理后,绘制成如图所示的不完整的统计图.请根据图中所给的信息解答下列问题:
(1)在这次调查中,一共抽取了多少名学生?
(2)请通过计算补全条形统计图;
(3)如果初一年级共有1200名学生,请你估计该年级最想读科技类书籍的学生有多少名.
【解答】解:(1)由题意知,一共抽取了(名)学生,
∴一共抽取了60名学生;
(2)由题意知,国防的人数为60﹣18﹣9﹣12﹣6=15(人),
补图如下:
(3)由题意知,(名),
∴估计该年级最想读科技类书籍的学生有180名.
20.(2023秋 安宁区校级期末)下面是小华同学解方组的过程,请你观察计算过程,回答下面问
题.
解:②×2得:8x﹣2y=﹣6③…(1)
①+③得:11x=﹣5…(2)
∴x(3)
(a)第 (1) 步(填序号)出错;
(b)请你写出正确的解题过程.
【解答】解:(a)第(1)步出错,
故答案为:(1);
(b),
②×2得:8x﹣2y=﹣12③,
①+③得:11x=﹣11,
∴x=﹣1,
把x=﹣1代入②,得y=2,
所以方程组的解是.
21.(2023秋 利辛县校级期末)如图,CD是△ABC的角平分线,点E在是AC上,BE交CD于点F,∠ACB=56°.
(1)若BE⊥AC,求∠DFB的度数;
(2)若BE⊥CD,∠A=50°,求∠ABE的度数.
【解答】解:(1)∵CD是∠ACB的平分线,
∴,
∵BE⊥AC,
∴∠CEF=90°.
∴∠EFC=90°﹣∠ACD=62°,
∴∠DFB=∠EFC=62°;
(2)∵BE⊥CD,CD是∠ACB 的平分线,
∴∠CFE=90°,∠ACD=28°,
∴∠CEB=180°﹣∠CFE﹣∠ACD=62°,
∴∠AEB=180°﹣∠CEB=118°,
∴∠ABE=180°﹣∠AEB﹣∠A=180°﹣118°﹣50°=12°.
22.(2023秋 金安区校级期末)在一次机器“猫”抓机器“鼠”的展演测试中,“鼠”先从起点出发,1min后,“猫”从同起点出发去追“鼠”,抓住“鼠”并稍作停留后,“猫”抓着“鼠”沿原路返回.“鼠”、“猫距起点的距离y(m)与时间x(min)之间的关系如图所示.
(1)在“猫”追“鼠”的过程中,“鼠”的平均速度是 5 m/min;
(2)求AB所在直线的函数表达式;
(3)求“猫”从起点出发到返回至起点所用的时间.
【解答】解:(1)由图象知:“鼠”6min跑了30m,
∴“鼠”的速度为:30÷6=5(m/min),
∴“鼠”的平均速度为5m/min;
(2)设AB的解析式为:y=kx+b,
∵图象经过A(7,30)和B(10,18),
把点A和点B坐标代入函数解析式得:
,
解得:,
∴AB的解析式为:y=﹣4x+58;
(3)令y=0,则﹣4x+58=0,
∴x=14.5,
∵“猫”比“鼠”迟一分钟出发,
∴“猫”从起点出发到返回至起点所用的时间为14.5﹣1=13.5(min).
答:“猫”从起点出发到返回至起点所用的时间为13.5min.
23.(2023秋 安宁区校级期末)如图,直线y1=2x﹣2的图象与y轴交于点A,直线y2=﹣2x+6的图象与y轴交于点B,两者相交于点C.
(1)方程组的解是 ;
(2)当y1>0与y2>0同时成立时,x的取值范围为 1<x<3 ;
(3)求△ABC的面积.
【解答】解:(1)如图所示:方程组组的解为:;
故答案为:;
(2)如图所示:当y1>0与y2>0同时成立时,
x取何值范围是:1<x<3;
故答案为:1<x<3;
(3)∵令x=0,则y1=﹣2,y2=6,
∴A(0,﹣2),B(0,6).
∴AB=8.
∴S△ABC8×2=8.
24.(2023秋 桐城市校级期末)某公司销售A型和B型两种电脑,其中A型电脑每台利润为400元,B型电脑每台利润为500元.该公司计划一次性购进这两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
(1)求y关于x的函数关系式;
(2)该商店购进A型、B型电脑各多少台,才能使销售总利润最大,最大利润是多少?
(3)实际进货时,厂家对A型电脑出厂价下调a(0<a<200)元,若该公司保持这两种型号电脑的售价不变,并且无论该公司如何进货这100台电脑的销售利润不变,求a的值.
【解答】解:(1)根据题意,y=400x+500(100﹣x)=﹣100x+50000;
(2)∵100﹣x≤2x,
∴x,
∵y=﹣100x+50000中k=﹣100<0,
∴y随x的增大而减小,
∵x为整数,
∴x=34时,y取得最大值,最大值为46600,
答:该商店购进A型34台、B型电脑66台,才能使销售总利润最大,最大利润是46600元;
(3)据题意得,y=(400+a)x+500(100﹣x),即y=(a﹣100)x+50000,
当a=100时,无论该公司如何进货这100台电脑的销售利润不变.
25.(2023秋 台江区期末)在数学实践活动课上,小亮同学利用一副三角尺探索与研究共直角顶点的两个直角三角形中的位置关系与数量关系.(其中∠A=30°,∠B=60°,∠C=∠D=45°)
(1)将三角尺如图1所示叠放在一起.
①∠AOD与∠BOC大小关系是 相等 ;
②∠BOD与∠AOC的数量关系是 ∠BOD+∠AOC=180° .
(2)小亮固定其中一块三角尺△COD不变,绕点O顺时针转动另一块三角尺,从图2的OA与OC重合开始,到图3的OA与OC在一条直线上时结束,探索△AOB的一边与△COD的一边平行的情况.
①求当AB∥CD时,如图4所示,∠AOC的大小;
②直接写出∠AOC的其余所有可能值.
【解答】解:(1)①∠AOD与∠BOC大小关系是相等;
∵∠AOD+∠AOC=90°,∠BOC+∠AOC=90°,
∴∠AOD=∠BOC,
故答案为:相等;
②∠BOD与∠AOC的数量关系是:∠BOD+∠AOC=180°;
∵∠DOC=90°,∠AOB=∠BOC+∠AOC=90°,
∴∠BOD+∠AOC=∠COD+∠COB+∠AOC=180°;
(2)①过点O作OE∥AB,如图4.1,
∵AB∥CD,
∴AB∥CD∥OE,
∴∠AOE=∠A=30°,∠COE=∠C=45°,
∴∠AOC=∠AOE+∠COE=75°;
②当AB∥OC时,如图4.2,则∠AOC=∠A=30°;
当OA∥CD时,如图4.3,则∠AOC=∠C=45°;
当AB∥OD时,如图4.4,则∠BOD=∠B=60°,
∴∠AOC=360°﹣90°﹣90°﹣∠BOD=120°;
当OB∥CD时,如图4.5,则∠BOD=∠D=45°,
∴∠AOC=360°﹣90°﹣90°﹣∠BOD=135°;
综上所述:∠AOC的其余可能值为30°或45°或120°或135°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
