专题六 分式方程 课件(59张PPT)2025届中考数学一轮复习
文档属性
| 名称 | 专题六 分式方程 课件(59张PPT)2025届中考数学一轮复习 |  | |
| 格式 | pptx | ||
| 文件大小 | 13.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-15 09:33:23 | ||
图片预览










文档简介
(共59张PPT)
专题六 分式方程
中考数学一轮复习备考合集
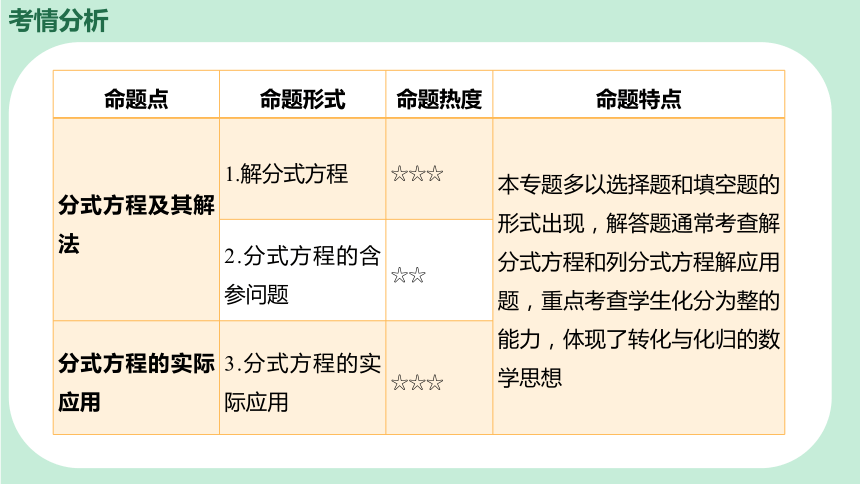
考情分析
命题点 命题形式 命题热度 命题特点
分式方程及其解法 1.解分式方程 ☆☆☆ 本专题多以选择题和填空题的形式出现,解答题通常考查解分式方程和列分式方程解应用题,重点考查学生化分为整的能力,体现了转化与化归的数学思想
2.分式方程的含参问题 ☆☆ 分式方程的实际应用 3.分式方程的实际应用 ☆☆☆
讲解一:
分式方程的概念及解法
知识复习
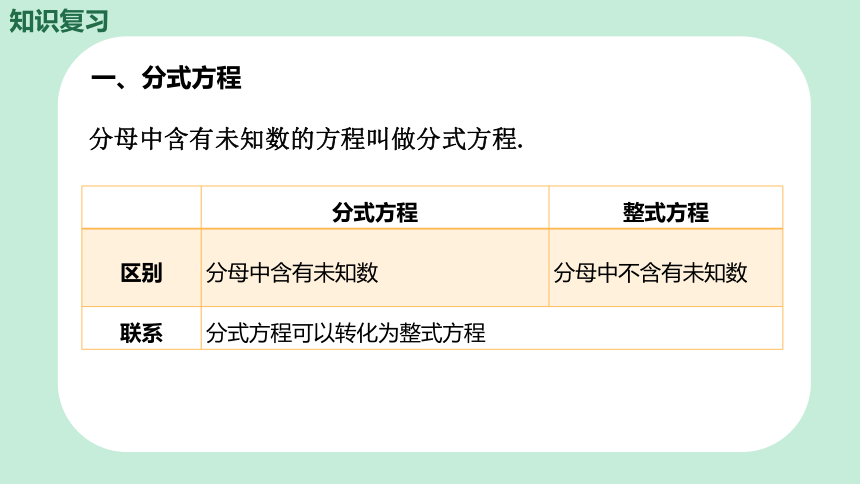
一、分式方程
分母中含有未知数的方程叫做分式方程.
分式方程 整式方程
区别 分母中含有未知数 分母中不含有未知数
联系 分式方程可以转化为整式方程
知识复习
一、分式方程
【注意】
(1)判断一个方程是否为分式方程,要掌握以下三点:
① 是方程;② 方程中含有分母;③ 分母中含有未知数.
(2)并不是含有分母的方程就是分式方程,必须是分母中含有未知数的方程才是分式方程.
知识复习
二、解分式方程
解分式方程的基本思路是通过去分母把分式方程转化为整式方程,再求解.
①去分母
方程两边同乘最简公分母,化为整式方程
②解方程
解整式方程
知识复习
二、解分式方程
③检验
把整式方程的解代入最简公分母
最简公分母不为0,是分式方程的解
最简公分母为0,不是分式方程的解,是增根.
知识复习
二、解分式方程
④写解
1.检验是解分式方程必不可少的步骤
2.分式方程无解,可能是解为增根,也可能是去分母后的整式方程无解
【注意】
3.用分式方程中的最简公分母同乘方程的两边,从而约去分母,但要注意用最简公分母乘方程两边各项时,不要漏乘不含分母的项.
知识复习
二、解分式方程
【拓展延伸】
对增根产生的原因理解如下:增根是在解分式方程的第一步,即去分母时产生的,根据方程的同解原理,方程两边都乘(或除以)同一个不为0的数,所得方程是原方程的同解方程.如果方程的两边同时乘0,那么所得方程与原方程不是同解方程,这时求得的根就是原方程的增根.
知识复习
三、分式方程的含参问题
1.根据分式方程有增根求参数的值的解题思路:
先将分式方程化为整式方程,再将增根代入整式方程,从而求出参数的值.
2.根据分式方程解的情况求参数的值或取值范围的解题思路:
先将分式方程化为整式方程,并解整式方程,用含参数的代数式表示出整式方程的解,再结合分式方程解的情况列方程或不等式求出参数的值或取值范围,注意要考虑分式方程中分母不为0的限制条件.
命题形式1 解分式方程
D
【思路点拨】
本题考查解分式方程,根据解分式方程方法和步骤(去分母,去括号,移项,合并同类项,系数化为1,检验)求解,即可解题.
命题形式1 解分式方程
命题形式1 解分式方程
x = -1
【思路点拨】
本题考查了解分式方程,熟练掌握解分式方程的方法和步骤是解题的关键.
先去分母,转化为解一元一次方程,注意要检验是否有增根.
命题形式1 解分式方程
命题形式1 解分式方程
3
命题形式1 解分式方程
【题型解读】
此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
命题形式1 解分式方程
x = 3
命题形式1 解分式方程
命题形式1 解分式方程
【思路点拨】
本题主要考查了解分式方程,先去分母变分式方程为整式方程,然后再解整式方程,最后对方程的解进行检验即可.
命题形式1 解分式方程
命题形式1 解分式方程
【思路点拨】
本题考查的是解分式方程,掌握分式方程的解法是解题关键,注意检验.依次去分母、去括号、移项、合并同类项求解,检验后即可得到答案.
命题形式1 解分式方程
命题形式2 分式方程的含参问题
A
命题形式2 分式方程的含参问题
命题形式2 分式方程的含参问题
B
命题形式2 分式方程的含参问题
A
命题形式2 分式方程的含参问题
命题形式2 分式方程的含参问题
-1
【思路点拨】
本题考查了根据分式方程的解的情况求参数,解分式方程求出分式方程的解,由解是正整数,确定出整数m的值即可.
命题形式2 分式方程的含参问题
命题形式2 分式方程的含参问题
12
命题形式2 分式方程的含参问题
命题形式2 分式方程的含参问题
命题形式2 分式方程的含参问题
-1
命题形式2 分式方程的含参问题
讲解二:
分式方程的实际应用
知识复习
列分式方程常用的等量关系
知识复习
列分式方程解应用题的一般步骤:
(1)审:审清题意,弄清已知量和未知量;找出已知的或隐含的等量关系,常用表格分析法.
(2)设:设未知数(既可以设直接未知数,也可以设间接未知数).
(3)列:列出分式方程.
(4)解:解这个方程.
(5)验:检验,既要检验所求得的根是不是所列分式方程的解,又要检验所求得的根是否符合实际意义.
(6)答:写出答案.
知识复习
【注意】
(1)在实际问题中,有时题目中包含多个相等的数量关系,在列方程时一定要选择一个能够体现全部(或大部分)题意的等量关系.
(2)在检验过程中,不仅要检验所得的根是否为原分式方程的根,还要检验这个根在实际问题中是否具有实际意义,如时间非负,人数非负等.
(3)在一些实际问题中,有时直接设问题所求的量为未知数比较麻烦,所以可以间接地设未知数.
(4)设一个未知数不容易表示等量关系时,还可以设多个未知数,即设辅助未知数.
命题形式3 分式方程的实际应用
A
命题形式3 分式方程的实际应用
命题形式3 分式方程的实际应用
D
命题形式3 分式方程的实际应用
命题形式3 分式方程的实际应用
命题形式3 分式方程的实际应用
D
命题形式3 分式方程的实际应用
命题形式3 分式方程的实际应用
A
命题形式3 分式方程的实际应用
命题形式3 分式方程的实际应用
B
命题形式3 分式方程的实际应用
命题形式3 分式方程的实际应用
命题形式3 分式方程的实际应用
命题形式3 分式方程的实际应用
命题形式3 分式方程的实际应用
命题形式3 分式方程的实际应用
命题形式3 分式方程的实际应用
命题形式3 分式方程的实际应用
命题形式3 分式方程的实际应用
命题形式3 分式方程的实际应用
我们下节课再见
See you in the next video
专题六 分式方程
中考数学一轮复习备考合集
考情分析
命题点 命题形式 命题热度 命题特点
分式方程及其解法 1.解分式方程 ☆☆☆ 本专题多以选择题和填空题的形式出现,解答题通常考查解分式方程和列分式方程解应用题,重点考查学生化分为整的能力,体现了转化与化归的数学思想
2.分式方程的含参问题 ☆☆ 分式方程的实际应用 3.分式方程的实际应用 ☆☆☆
讲解一:
分式方程的概念及解法
知识复习
一、分式方程
分母中含有未知数的方程叫做分式方程.
分式方程 整式方程
区别 分母中含有未知数 分母中不含有未知数
联系 分式方程可以转化为整式方程
知识复习
一、分式方程
【注意】
(1)判断一个方程是否为分式方程,要掌握以下三点:
① 是方程;② 方程中含有分母;③ 分母中含有未知数.
(2)并不是含有分母的方程就是分式方程,必须是分母中含有未知数的方程才是分式方程.
知识复习
二、解分式方程
解分式方程的基本思路是通过去分母把分式方程转化为整式方程,再求解.
①去分母
方程两边同乘最简公分母,化为整式方程
②解方程
解整式方程
知识复习
二、解分式方程
③检验
把整式方程的解代入最简公分母
最简公分母不为0,是分式方程的解
最简公分母为0,不是分式方程的解,是增根.
知识复习
二、解分式方程
④写解
1.检验是解分式方程必不可少的步骤
2.分式方程无解,可能是解为增根,也可能是去分母后的整式方程无解
【注意】
3.用分式方程中的最简公分母同乘方程的两边,从而约去分母,但要注意用最简公分母乘方程两边各项时,不要漏乘不含分母的项.
知识复习
二、解分式方程
【拓展延伸】
对增根产生的原因理解如下:增根是在解分式方程的第一步,即去分母时产生的,根据方程的同解原理,方程两边都乘(或除以)同一个不为0的数,所得方程是原方程的同解方程.如果方程的两边同时乘0,那么所得方程与原方程不是同解方程,这时求得的根就是原方程的增根.
知识复习
三、分式方程的含参问题
1.根据分式方程有增根求参数的值的解题思路:
先将分式方程化为整式方程,再将增根代入整式方程,从而求出参数的值.
2.根据分式方程解的情况求参数的值或取值范围的解题思路:
先将分式方程化为整式方程,并解整式方程,用含参数的代数式表示出整式方程的解,再结合分式方程解的情况列方程或不等式求出参数的值或取值范围,注意要考虑分式方程中分母不为0的限制条件.
命题形式1 解分式方程
D
【思路点拨】
本题考查解分式方程,根据解分式方程方法和步骤(去分母,去括号,移项,合并同类项,系数化为1,检验)求解,即可解题.
命题形式1 解分式方程
命题形式1 解分式方程
x = -1
【思路点拨】
本题考查了解分式方程,熟练掌握解分式方程的方法和步骤是解题的关键.
先去分母,转化为解一元一次方程,注意要检验是否有增根.
命题形式1 解分式方程
命题形式1 解分式方程
3
命题形式1 解分式方程
【题型解读】
此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
命题形式1 解分式方程
x = 3
命题形式1 解分式方程
命题形式1 解分式方程
【思路点拨】
本题主要考查了解分式方程,先去分母变分式方程为整式方程,然后再解整式方程,最后对方程的解进行检验即可.
命题形式1 解分式方程
命题形式1 解分式方程
【思路点拨】
本题考查的是解分式方程,掌握分式方程的解法是解题关键,注意检验.依次去分母、去括号、移项、合并同类项求解,检验后即可得到答案.
命题形式1 解分式方程
命题形式2 分式方程的含参问题
A
命题形式2 分式方程的含参问题
命题形式2 分式方程的含参问题
B
命题形式2 分式方程的含参问题
A
命题形式2 分式方程的含参问题
命题形式2 分式方程的含参问题
-1
【思路点拨】
本题考查了根据分式方程的解的情况求参数,解分式方程求出分式方程的解,由解是正整数,确定出整数m的值即可.
命题形式2 分式方程的含参问题
命题形式2 分式方程的含参问题
12
命题形式2 分式方程的含参问题
命题形式2 分式方程的含参问题
命题形式2 分式方程的含参问题
-1
命题形式2 分式方程的含参问题
讲解二:
分式方程的实际应用
知识复习
列分式方程常用的等量关系
知识复习
列分式方程解应用题的一般步骤:
(1)审:审清题意,弄清已知量和未知量;找出已知的或隐含的等量关系,常用表格分析法.
(2)设:设未知数(既可以设直接未知数,也可以设间接未知数).
(3)列:列出分式方程.
(4)解:解这个方程.
(5)验:检验,既要检验所求得的根是不是所列分式方程的解,又要检验所求得的根是否符合实际意义.
(6)答:写出答案.
知识复习
【注意】
(1)在实际问题中,有时题目中包含多个相等的数量关系,在列方程时一定要选择一个能够体现全部(或大部分)题意的等量关系.
(2)在检验过程中,不仅要检验所得的根是否为原分式方程的根,还要检验这个根在实际问题中是否具有实际意义,如时间非负,人数非负等.
(3)在一些实际问题中,有时直接设问题所求的量为未知数比较麻烦,所以可以间接地设未知数.
(4)设一个未知数不容易表示等量关系时,还可以设多个未知数,即设辅助未知数.
命题形式3 分式方程的实际应用
A
命题形式3 分式方程的实际应用
命题形式3 分式方程的实际应用
D
命题形式3 分式方程的实际应用
命题形式3 分式方程的实际应用
命题形式3 分式方程的实际应用
D
命题形式3 分式方程的实际应用
命题形式3 分式方程的实际应用
A
命题形式3 分式方程的实际应用
命题形式3 分式方程的实际应用
B
命题形式3 分式方程的实际应用
命题形式3 分式方程的实际应用
命题形式3 分式方程的实际应用
命题形式3 分式方程的实际应用
命题形式3 分式方程的实际应用
命题形式3 分式方程的实际应用
命题形式3 分式方程的实际应用
命题形式3 分式方程的实际应用
命题形式3 分式方程的实际应用
命题形式3 分式方程的实际应用
我们下节课再见
See you in the next video
同课章节目录
