用函数模型解决函数问题
图片预览







文档简介
课件20张PPT。4.2.2:用函数模型解决实际问题 函数模型是应用最广泛的数学模型之一,许多实际问题一旦认定是函数关系,就可以通过研究函数的性质把握问题,使问题得到解决。教学目的及重点
理解解决应用题的步骤及思维方式,能利用信息技术帮助理解应用问题。
教学难点:建立恰当的数学模型。1.一次函数的解析式为__________________ , 其图像是一条____线,
当________时,一次函数在 上为增函数,当_______时,
一次函数在 上为减函数。2.二次函数的解析式为_______________________, 其图像是一条
________线,当______时,函数有最小值为___________,当______
时,函数有最大值为____________。直抛物例1 某公司一年需要一种计算机元件8000个,每天需同样多的元件用于组装整机,该元件每年分n次进货,每次购买元件的数量均为x,购一次货需要手续费500元,已购进而未使用的元件要付库存费,可以认为平均库存量为x/2件,每个元件的库存费是一年2元,请核算一下,每年进货几次花费最小?分析:
1,每次进货量x与进货次数n有什么关系:
2,进货次数为:
3,全年的手续费是:
4,一年的总库存费为:
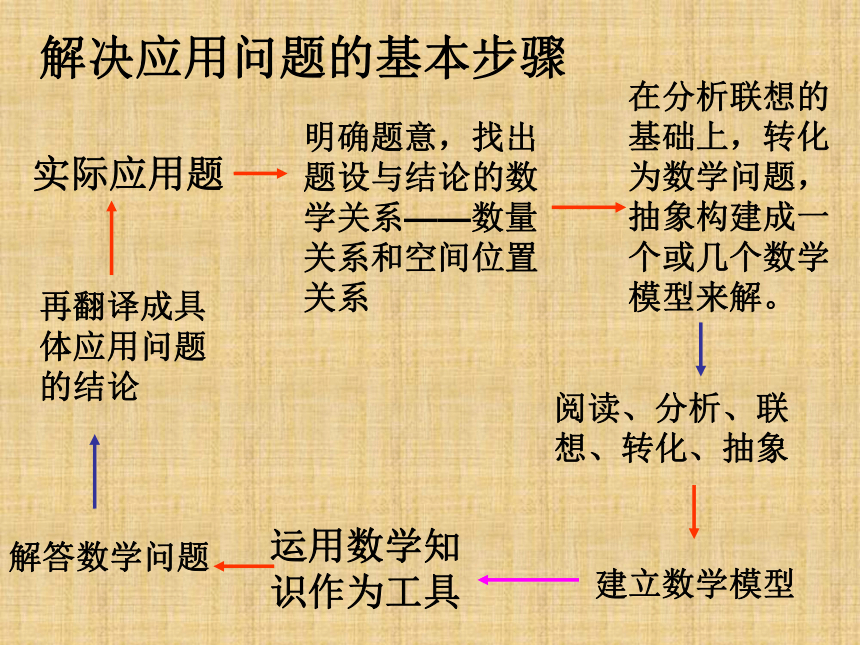
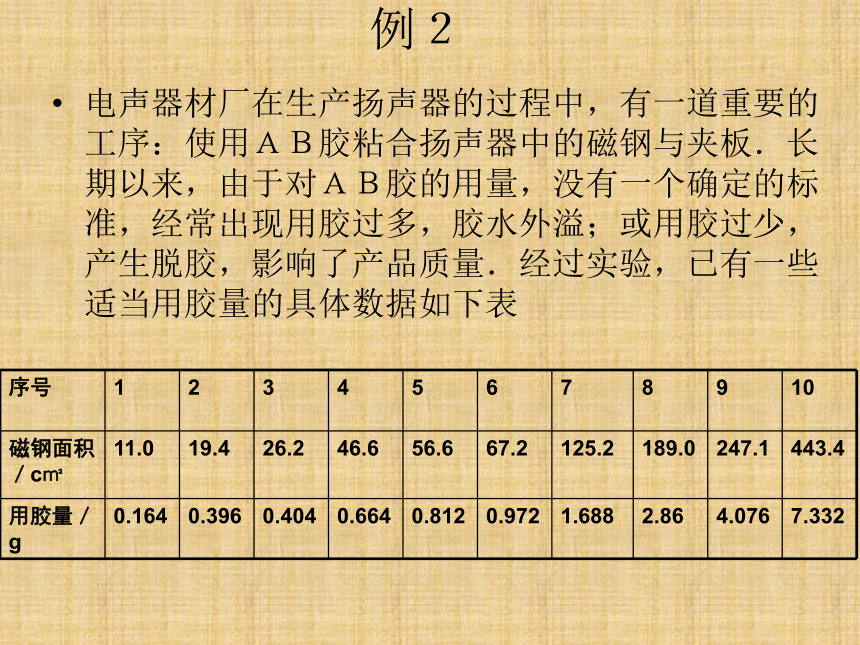
5,其它费用:C解决应用问题的基本步骤实际应用题明确题意,找出题设与结论的数学关系——数量关系和空间位置关系在分析联想的基础上,转化为数学问题,抽象构建成一个或几个数学模型来解。阅读、分析、联想、转化、抽象建立数学模型运用数学知识作为工具解答数学问题再翻译成具体应用问题的结论例2 电声器材厂在生产扬声器的过程中,有一道重要的工序:使用AB胶粘合扬声器中的磁钢与夹板.长期以来,由于对AB胶的用量,没有一个确定的标准,经常出现用胶过多,胶水外溢;或用胶过少,产生脱胶,影响了产品质量.经过实验,已有一些适当用胶量的具体数据如下表取点(56.6,0.812),(189.0,2.86),将他们的坐标代入y=ax+b,得方程组 {0.182=56.6a+b2.86=189.0a+b解得 a=0.01547,b=-0.06350.这条直线是y=0.01547x-0.06350例2已知某商品的价格每上涨x%,销售的数量就减少kx%,其中k为正常数。
1. 当 时,该商品的价格上涨多少,就能使销售的总金额最大?
2. 如果适当的涨价,能使销售总金额增加,求k的取值范围。解:1.设商品现在定价a元,卖出的数量为b个。
由题设:当价格上涨x%时,销售总额为
即
取 得:
当 x = 50时, 即该商品的价格上涨50%时,销售总金额最大。2.∵二次函数
在 上递增,
在 上递减
∴适当地涨价,即 x > 0 , 即
就是 0 < k <1 , 能使销售总金额增加。例3某乡镇现在人均一年占有粮食360千克,如果该乡镇人口平均每年增长1.2%,粮食总产量平均每年增长4%,那么x年后若人均一年占有y千克粮食,求出函数y关于x的解析式.解:设该乡镇现在人口量为M,则该乡镇现在一年的粮食总产量360M,经过1年后,该乡镇粮食总产量为360M(1+4%),人口量为M(1+1.2%)则人均占有粮食为
经过2年后,人均占有粮食为
……
经过x年后,人均占有粮食
y=
即所求函数式为: y=360( )x例4(本例2)电器材厂在生产扬声器的过程中,有一道重要的工序:使用AB胶粘合扬声器中的钢与夹板。长期以来,由于对AB胶的用量没有一个确定的标准,经常出现用胶过多,脱水外溢;或用胶过少,产生脱胶,影响了产品质量。经过实验,已有一些恰当用胶量的具体数据(见表4-3)现在需要提出一个既科学又简便的方法来确定磁钢面积与用胶量的关系。例5某地区不同身高的未成年男性的体重平均值如表:
(1)根据表提供的的数据,能否建立一个恰当的函数模型,使它能比较近似地反映这个地区一体化未成年男性体重ykg与身高xcm的函数关系?试写出这个函数模型的关系式;(2)若体重超过相同身高男性体重的平均值的1.2倍为偏胖,低于0.8倍为偏瘦,那么这个地区一名身高为175cm,体重为78kg的在校男生的体重是否正常?解:(1)以身高为横坐标,体重为纵坐标,画出散点图,根据图的分布特点,设y=a.bx这一函数来近似刻画其关系;取两点(70,7.90),(160,47.25),代入
y=a.bx得:
用计算器得:a?2, b?1.02
这样就得到函数模型:y=2?1.02x为所求解析式;(2)将x=175代入y=2?1.02x,得
y=2?1.02175,用计算器得:y?63.98.
由于78?63.98?1.22>1.2,所以这个男生偏胖。练习P142作业P148:A组:2; B组:1小结:掌握解决应用题的步骤及思维方式。
见开始
理解解决应用题的步骤及思维方式,能利用信息技术帮助理解应用问题。
教学难点:建立恰当的数学模型。1.一次函数的解析式为__________________ , 其图像是一条____线,
当________时,一次函数在 上为增函数,当_______时,
一次函数在 上为减函数。2.二次函数的解析式为_______________________, 其图像是一条
________线,当______时,函数有最小值为___________,当______
时,函数有最大值为____________。直抛物例1 某公司一年需要一种计算机元件8000个,每天需同样多的元件用于组装整机,该元件每年分n次进货,每次购买元件的数量均为x,购一次货需要手续费500元,已购进而未使用的元件要付库存费,可以认为平均库存量为x/2件,每个元件的库存费是一年2元,请核算一下,每年进货几次花费最小?分析:
1,每次进货量x与进货次数n有什么关系:
2,进货次数为:
3,全年的手续费是:
4,一年的总库存费为:
5,其它费用:C解决应用问题的基本步骤实际应用题明确题意,找出题设与结论的数学关系——数量关系和空间位置关系在分析联想的基础上,转化为数学问题,抽象构建成一个或几个数学模型来解。阅读、分析、联想、转化、抽象建立数学模型运用数学知识作为工具解答数学问题再翻译成具体应用问题的结论例2 电声器材厂在生产扬声器的过程中,有一道重要的工序:使用AB胶粘合扬声器中的磁钢与夹板.长期以来,由于对AB胶的用量,没有一个确定的标准,经常出现用胶过多,胶水外溢;或用胶过少,产生脱胶,影响了产品质量.经过实验,已有一些适当用胶量的具体数据如下表取点(56.6,0.812),(189.0,2.86),将他们的坐标代入y=ax+b,得方程组 {0.182=56.6a+b2.86=189.0a+b解得 a=0.01547,b=-0.06350.这条直线是y=0.01547x-0.06350例2已知某商品的价格每上涨x%,销售的数量就减少kx%,其中k为正常数。
1. 当 时,该商品的价格上涨多少,就能使销售的总金额最大?
2. 如果适当的涨价,能使销售总金额增加,求k的取值范围。解:1.设商品现在定价a元,卖出的数量为b个。
由题设:当价格上涨x%时,销售总额为
即
取 得:
当 x = 50时, 即该商品的价格上涨50%时,销售总金额最大。2.∵二次函数
在 上递增,
在 上递减
∴适当地涨价,即 x > 0 , 即
就是 0 < k <1 , 能使销售总金额增加。例3某乡镇现在人均一年占有粮食360千克,如果该乡镇人口平均每年增长1.2%,粮食总产量平均每年增长4%,那么x年后若人均一年占有y千克粮食,求出函数y关于x的解析式.解:设该乡镇现在人口量为M,则该乡镇现在一年的粮食总产量360M,经过1年后,该乡镇粮食总产量为360M(1+4%),人口量为M(1+1.2%)则人均占有粮食为
经过2年后,人均占有粮食为
……
经过x年后,人均占有粮食
y=
即所求函数式为: y=360( )x例4(本例2)电器材厂在生产扬声器的过程中,有一道重要的工序:使用AB胶粘合扬声器中的钢与夹板。长期以来,由于对AB胶的用量没有一个确定的标准,经常出现用胶过多,脱水外溢;或用胶过少,产生脱胶,影响了产品质量。经过实验,已有一些恰当用胶量的具体数据(见表4-3)现在需要提出一个既科学又简便的方法来确定磁钢面积与用胶量的关系。例5某地区不同身高的未成年男性的体重平均值如表:
(1)根据表提供的的数据,能否建立一个恰当的函数模型,使它能比较近似地反映这个地区一体化未成年男性体重ykg与身高xcm的函数关系?试写出这个函数模型的关系式;(2)若体重超过相同身高男性体重的平均值的1.2倍为偏胖,低于0.8倍为偏瘦,那么这个地区一名身高为175cm,体重为78kg的在校男生的体重是否正常?解:(1)以身高为横坐标,体重为纵坐标,画出散点图,根据图的分布特点,设y=a.bx这一函数来近似刻画其关系;取两点(70,7.90),(160,47.25),代入
y=a.bx得:
用计算器得:a?2, b?1.02
这样就得到函数模型:y=2?1.02x为所求解析式;(2)将x=175代入y=2?1.02x,得
y=2?1.02175,用计算器得:y?63.98.
由于78?63.98?1.22>1.2,所以这个男生偏胖。练习P142作业P148:A组:2; B组:1小结:掌握解决应用题的步骤及思维方式。
见开始
