八上数学：2.4-估算

(共18张PPT)
2.4 估算
第二章 实数
导入新课
讲授新课
当堂练习
课堂小结
情境引入
学习目标
1.了解估算的基本方法.(重点)
2.能够运用估算解决生活中的实际问题.(难点)
导入新课
观察与思考
某地开辟了一块长方形荒地，新建一个以环保为主题的公园.已知这块荒地的长是宽的2倍，它的面积为400000m2.
(1)公园的宽大约是多少？它有1000m吗？
1000
2000
S=400000
∵2000×1000=2000000 >400000，
∴公园的宽没有1 000m.
(2)如果要求误差小于10米，它的宽大约是多少？
x
2x
S=400000
x 2x=400000,
2x2=400000,
x2=200000,
x=
大约是多少呢？
解：设公园的宽为x米.
讲授新课
估算的基本方法
一
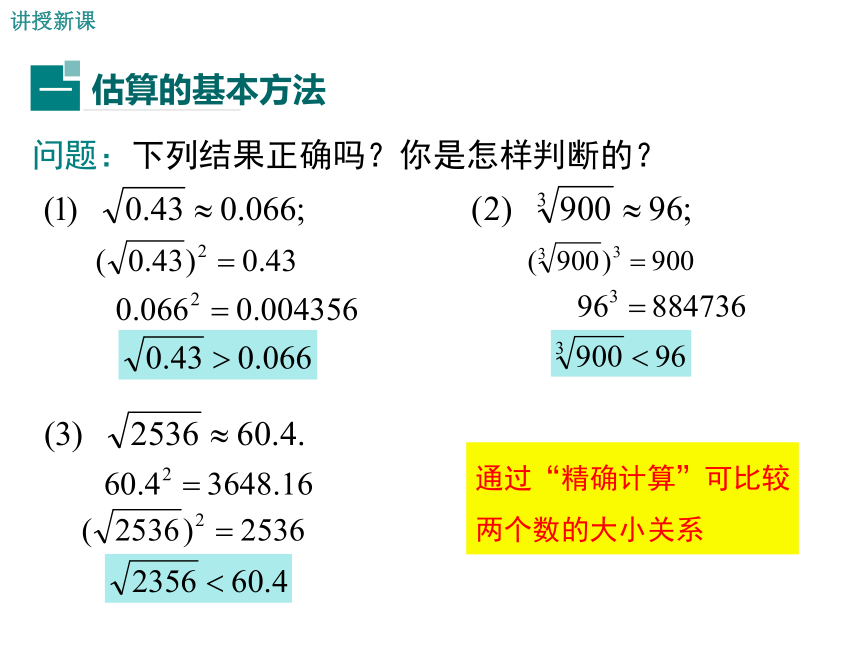
问题：下列结果正确吗？你是怎样判断的？
通过“精确计算”可比较
两个数的大小关系
通过“估算”也可比较
两个数的大小关系
估算无理数大小的方法：
(1)利用乘方与开方互为逆运算来确定无理数的整数部分；
(2)根据所要求的误差确定小数部分.
要点归纳
所以 的值约是3.5或3.6.
例1：怎样估算无理数 (误差小于0.1)？
的整数部分是3，
典例精析
按要求估算下列无理数：
解：
练一练
例2：生活经验表明，靠墙摆放梯子时，若梯子底端离墙的距离约为梯子长度的 ，则梯子比较稳定.现有一长为6 m的梯子，当梯子稳定摆放时，它的顶端能达到5.6m高的墙头吗
解：设梯子稳定摆放时的高度为x m，此时梯子底端离墙的距离恰为梯子长度的 ，根据勾股定理
6
所以梯子稳定摆放时，它的顶端能够达到5.6m高的墙头.
例3：通过估算，比较 与 的大小.
解：
用估算法比较数的大小
二
方法归纳
两个带根号的无理数比较大小的结论：
1.
2.
3. 若a,b都为正数，则
方法归纳
对于含根号的数比较大小，一般可采取下列方法：
1.先估算含根号的数的近似值，再和另一个数进行比较；
2.当符合相同时，把不含根号的数平方，和被开方数比较，本方法的实质是比较被开方数，被开方数越大，其算术平方根越大；
3.若同分母或同分子的，可比较它们的分子或分母的大小.
当堂练习
1.通过估算,比较下面各组数的大小:
2. 一个人一生平均要饮用的液体总量大约为40m3 .如果用一圆柱形的容器（底面直径等于高）来装这些液体，这个容器大约有多高？（结果精确到1 m）
解：设圆柱的高为 xm，那么它的底面半径为0.5xm,
则:
3.小丽想用一块面积为400cm2的正方形纸片，沿着边的方向裁出一块面积为300cm2的长方形纸片，使它的长宽之比为3∶2.她不知能否裁得出来，正在发愁.小明见了说：“别发愁，一定能用一块面积大的纸片裁出一块面积小的纸片.”你同意小明的说法吗？小丽能用这块纸片裁出符合要求的纸片吗？Z
解:由题意知正方形纸片的边长为20cm.
设长方形的长为3x cm,则宽为2x cm.则有
估算
估算的基本方法
课堂小结
估算在生活中的应用