北师大版八上第六章第一节《平均数第一课时》课件
文档属性
| 名称 | 北师大版八上第六章第一节《平均数第一课时》课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-14 17:15:56 | ||
图片预览






文档简介
(共14张PPT)
北师大版数学八年级上册第六单元
《平均数(1)》
我们常说“某次考试中,甲班的成绩比乙班的成绩更好”,怎样理解“甲班的成绩比乙班的成绩更好”?
学习目标:
核心素养:数据分析、数学建模.
1、理解算术平均数、加权平均数的概念,会选用合适的方法求一组数据的算术平均数和加权平均数.
2、经历用平均数描述数据集中趋势的过程,体会数据中所蕴含的信息,发展数据分析观念;
3、体会算术平均数与加权平均数的联系与区别,发展应用意识.
[课前自主学习]
阅读课本第136-138页,完成下面问题:
问题1、小明所在小组的12位学生在某次数学考试中成绩如下(单位:分):91,88,90,88,91,90,91,93,88,87,88,93.求小明所在小组学生的平均分(结果保留一位小数).
解法1:
(91+88+90+88+91+90+91+93+88+87+88+93)÷12 ≈ 89.8(分)
平均数=数据的和÷数据的个数
解法2:以90分为基准,每个数据都减去90分得到12个新数据如下:
1,-2,0,-2,1,0,1,3,-2,-3,-2,3.求这组新数据的平均数为:
七年级上册引入负数后的新方法
(分)
解法中以90分为基准,为什么选择90为基准?
用平均数来描述一组数据的集中趋势.
91,88,90,88,91,90,91,93,88,87,88,93.
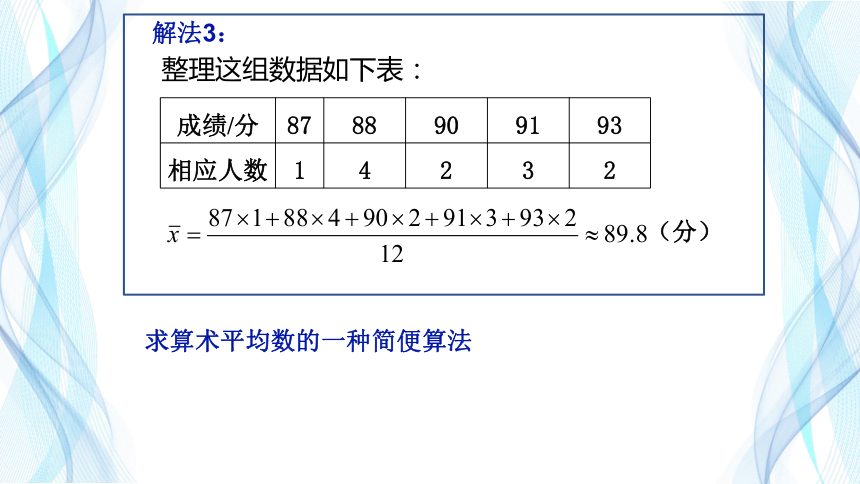
解法3:
求算术平均数的一种简便算法
整理这组数据如下表:
成绩/分 87 88 90 91 93
相应人数 1 4 2 3 2
(分)
例题:学校广播站招聘音乐鉴赏栏目策划人员一名,对A、B、C三名候选人进行了三项素质测试,他们各项测试成绩如下表所示:
测试项目 测试成绩 A B C
音乐知识 72 85 67
语言 50 74 70
普通话 88 45 67
(1)如果根据三项测试的平均成绩确定采用人选,那么谁将被录用?
(2)据实际需要,学校广播站将音乐知识、语言、普通话三项测试得分按4:3:1的比例确定各人的测试成绩,此时谁将被录用?
测试项目 测试成绩 A B C
音乐知识 72 85 67
语言 50 74 70
普通话 88 45 67
(1)如果根据三项测试的平均成绩确定采用人选,那么谁将被录用?
候选人A将被录用。
招
聘
音
乐
鉴
赏
栏
目
策
划
人
员
测试项目 测试成绩 A B C
音乐知识 72 85 67
语言 50 74 70
普通话 88 45 67
(2)据实际需要,学校广播站将音乐知识、语言、普通话三项测试得分按4:3:1的比例确定各人的测试成绩,此时谁将被录用?
候选人B将被录用。
(1)(2)的结果不同说明什么?
招
聘
音
乐
鉴
赏
栏
目
策
划
人
员
测试项目 测试成绩 A B C
音乐知识 72 85 67
语言 50 74 70
普通话 88 45 67
(2)据实际需要,学校广播站将音乐知识、语言、普通话三项测试得分按4:3:1的比例确定各人的测试成绩,此时谁将被录用?
招
聘
音
乐
鉴
赏
栏
目
策
划
人
员
合作探究
变式一:如果学校广播站招聘的是播音员,学校广播站将音乐知识、语言、普通话三项测试得分按1:3:4的比例确定各人的测试成绩,此时谁将被录用?
你觉得广播站调整的三项测试得分的权是否合适?
权的变化,直接导致结果不同,这既体现了权在求加权平均数的作用,又反映了应用统计知识解决实际问题时要灵活、体现知识要活学活用.
合作探究
变式二、老师在计算学期总平均分的时候按如下标准:作业占5%、平时测验占20%、期中占30%、期末考试占45%,小明的成绩如下表:
学生 作业 测验 期中考试 期末考试
小明 90 85 88 80
这里的权分别是什么?与之前的权的形式相比有什么变化?
权在不同的情境中表现形式可能不同,权有时表现为数据出现的次数,有时表现为百分比.
总结:
这节课学习了什么?你收获了什么?
(1)加权平均数在数据分析中的作用是什么?
(2)权的作用是什么?权的形式主要有哪些?
(3) 算术平均数与加权平均数的联系与区别有哪些?
北师大版数学八年级上册第六单元
《平均数(1)》
我们常说“某次考试中,甲班的成绩比乙班的成绩更好”,怎样理解“甲班的成绩比乙班的成绩更好”?
学习目标:
核心素养:数据分析、数学建模.
1、理解算术平均数、加权平均数的概念,会选用合适的方法求一组数据的算术平均数和加权平均数.
2、经历用平均数描述数据集中趋势的过程,体会数据中所蕴含的信息,发展数据分析观念;
3、体会算术平均数与加权平均数的联系与区别,发展应用意识.
[课前自主学习]
阅读课本第136-138页,完成下面问题:
问题1、小明所在小组的12位学生在某次数学考试中成绩如下(单位:分):91,88,90,88,91,90,91,93,88,87,88,93.求小明所在小组学生的平均分(结果保留一位小数).
解法1:
(91+88+90+88+91+90+91+93+88+87+88+93)÷12 ≈ 89.8(分)
平均数=数据的和÷数据的个数
解法2:以90分为基准,每个数据都减去90分得到12个新数据如下:
1,-2,0,-2,1,0,1,3,-2,-3,-2,3.求这组新数据的平均数为:
七年级上册引入负数后的新方法
(分)
解法中以90分为基准,为什么选择90为基准?
用平均数来描述一组数据的集中趋势.
91,88,90,88,91,90,91,93,88,87,88,93.
解法3:
求算术平均数的一种简便算法
整理这组数据如下表:
成绩/分 87 88 90 91 93
相应人数 1 4 2 3 2
(分)
例题:学校广播站招聘音乐鉴赏栏目策划人员一名,对A、B、C三名候选人进行了三项素质测试,他们各项测试成绩如下表所示:
测试项目 测试成绩 A B C
音乐知识 72 85 67
语言 50 74 70
普通话 88 45 67
(1)如果根据三项测试的平均成绩确定采用人选,那么谁将被录用?
(2)据实际需要,学校广播站将音乐知识、语言、普通话三项测试得分按4:3:1的比例确定各人的测试成绩,此时谁将被录用?
测试项目 测试成绩 A B C
音乐知识 72 85 67
语言 50 74 70
普通话 88 45 67
(1)如果根据三项测试的平均成绩确定采用人选,那么谁将被录用?
候选人A将被录用。
招
聘
音
乐
鉴
赏
栏
目
策
划
人
员
测试项目 测试成绩 A B C
音乐知识 72 85 67
语言 50 74 70
普通话 88 45 67
(2)据实际需要,学校广播站将音乐知识、语言、普通话三项测试得分按4:3:1的比例确定各人的测试成绩,此时谁将被录用?
候选人B将被录用。
(1)(2)的结果不同说明什么?
招
聘
音
乐
鉴
赏
栏
目
策
划
人
员
测试项目 测试成绩 A B C
音乐知识 72 85 67
语言 50 74 70
普通话 88 45 67
(2)据实际需要,学校广播站将音乐知识、语言、普通话三项测试得分按4:3:1的比例确定各人的测试成绩,此时谁将被录用?
招
聘
音
乐
鉴
赏
栏
目
策
划
人
员
合作探究
变式一:如果学校广播站招聘的是播音员,学校广播站将音乐知识、语言、普通话三项测试得分按1:3:4的比例确定各人的测试成绩,此时谁将被录用?
你觉得广播站调整的三项测试得分的权是否合适?
权的变化,直接导致结果不同,这既体现了权在求加权平均数的作用,又反映了应用统计知识解决实际问题时要灵活、体现知识要活学活用.
合作探究
变式二、老师在计算学期总平均分的时候按如下标准:作业占5%、平时测验占20%、期中占30%、期末考试占45%,小明的成绩如下表:
学生 作业 测验 期中考试 期末考试
小明 90 85 88 80
这里的权分别是什么?与之前的权的形式相比有什么变化?
权在不同的情境中表现形式可能不同,权有时表现为数据出现的次数,有时表现为百分比.
总结:
这节课学习了什么?你收获了什么?
(1)加权平均数在数据分析中的作用是什么?
(2)权的作用是什么?权的形式主要有哪些?
(3) 算术平均数与加权平均数的联系与区别有哪些?
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
