八年级下册:1.3.2-三角形三边的垂直平分线及作图
文档属性
| 名称 | 八年级下册:1.3.2-三角形三边的垂直平分线及作图 |

|
|
| 格式 | ppt | ||
| 文件大小 | 592.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-14 17:46:24 | ||
图片预览




文档简介
(共21张PPT)
1.3 线段的垂直平分线
第一章 三角形的证明
导入新课
讲授新课
当堂练习
课堂小结
第2课时 三角形三边的垂直平分线及作图
1.理解并掌握三角形三边的垂直平分线的性质,能
够运用其解决实际问题.(重点)
2.能够利用尺规作出三角形的垂直平分线.
学习目标
导入新课
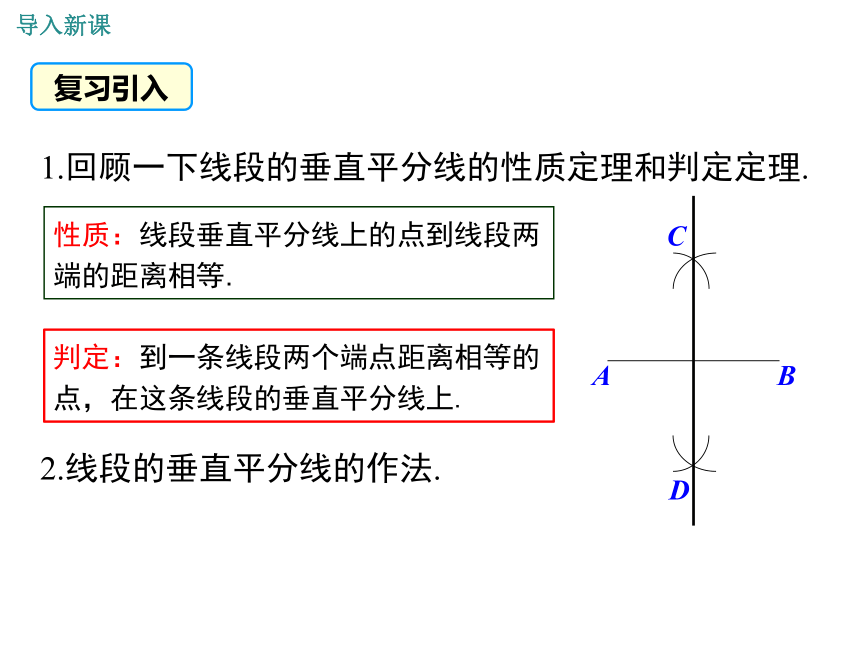
复习引入
A
B
C
D
1.回顾一下线段的垂直平分线的性质定理和判定定理.
2.线段的垂直平分线的作法.
性质:线段垂直平分线上的点到线段两端的距离相等.
判定:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
讲授新课
三角形三边的垂直平分线的性质
一
合作探究
画一画:利用尺规作三角形三条边的垂直平分线,完成之后你发现了什么?
发现:三角形三边的垂直平分线交于一点.这一点到三角形三个顶点的距离相等.
怎样证明这个结论呢
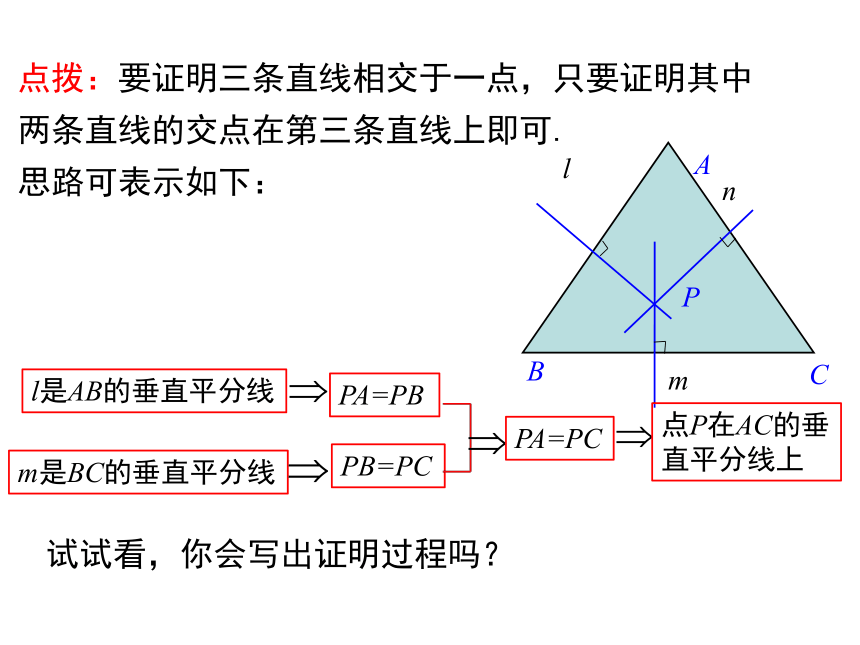
点拨:要证明三条直线相交于一点,只要证明其中两条直线的交点在第三条直线上即可.
思路可表示如下:
试试看,你会写出证明过程吗?
B
C
A
P
l
n
m
l是AB的垂直平分线
m是BC的垂直平分线
PA=PB
PB=PC
PA=PC
点P在AC的垂直平分线上
证明:连接PA,PB,PC.
∵点P在AB,AC的垂直平分线上, ∴PA=PB,PA=PC
(线段垂直平分线上 的点到线段两端距离相等).
∴PB=PC.
∴点P在BC的垂直平分线上
(到线段两端距离相等的点在线段的垂直平分线上).
B
C
A
P
l
n
m
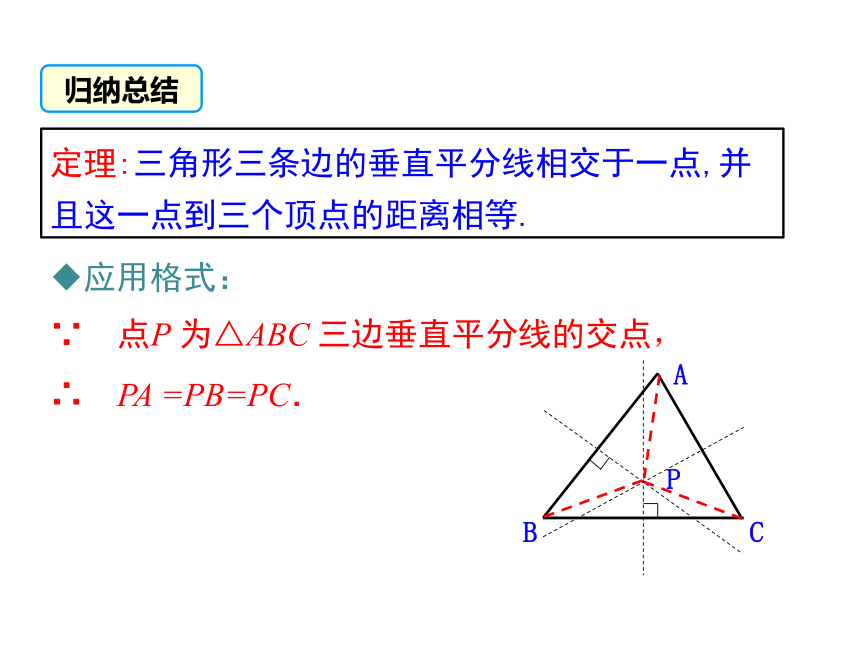
定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
归纳总结
应用格式:
∵ 点P 为△ABC 三边垂直平分线的交点,
∴ PA =PB=PC.
A
B
C
P
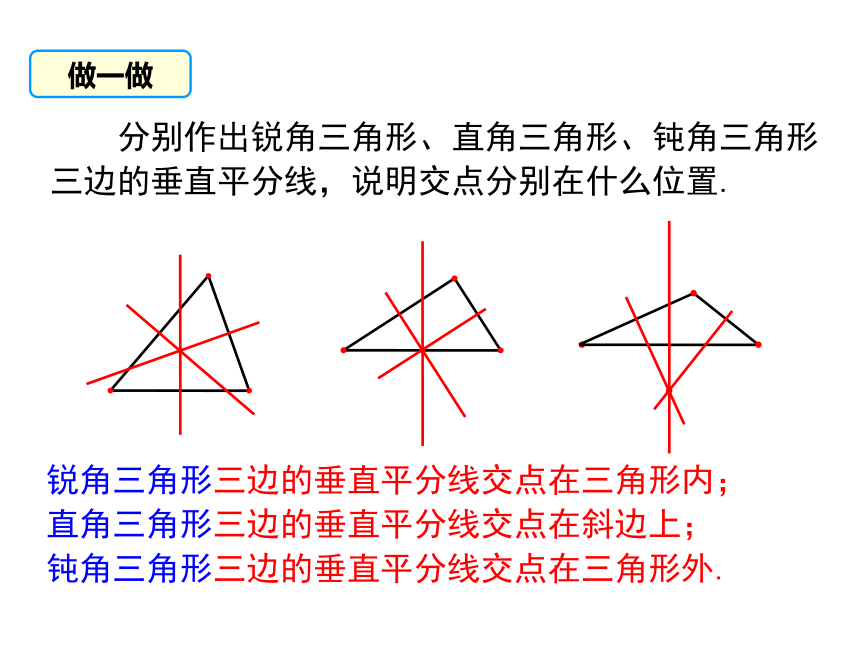
分别作出锐角三角形、直角三角形、钝角三角形三边的垂直平分线,说明交点分别在什么位置.
锐角三角形三边的垂直平分线交点在三角形内;
直角三角形三边的垂直平分线交点在斜边上;
钝角三角形三边的垂直平分线交点在三角形外.
做一做
尺规作图
二
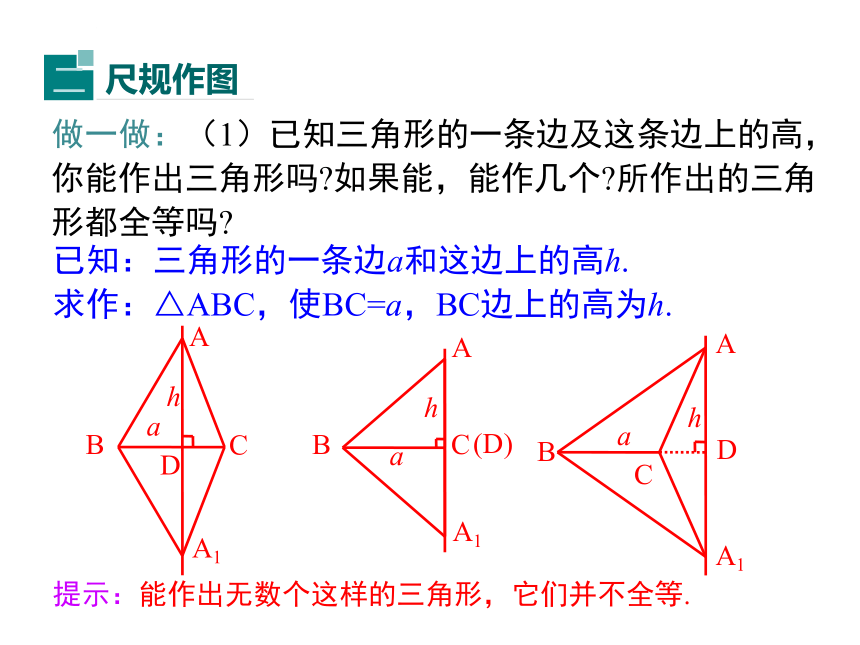
做一做:(1)已知三角形的一条边及这条边上的高,你能作出三角形吗 如果能,能作几个 所作出的三角形都全等吗
已知:三角形的一条边a和这边上的高h.
求作:△ABC,使BC=a,BC边上的高为h.
A1
D
C
B
A
a
h
(D)
C
B
A
a
h
A1
D
C
B
A
a
h
A1
提示:能作出无数个这样的三角形,它们并不全等.
(2)已知等腰三角形的底边,你能用尺规作出等腰三角形吗 如果能,能作几个 所作出的三角形都全等吗
这样的等腰三角形有无数多个.根据线段垂直平分线上的点到线段两个端点的距离相等,只要作底边的垂直平分线,取它上面除底边的中点外的任意一点,和底边的两个端点相连接,都可以得到一个等腰三角形.
如图所示,这些三角形不都全等.
(3)已知等腰三角形的底及底边上的高,你能用尺规作出等腰三角形吗?能作几个?
这样的等腰三角形只有两个,并且它们是全等的,分别位于已知底边的两侧.
例 已知:线段a,h.
求作:△ABC,使AB=AC,BC=a,高AD=h.
N
M
D
C
B
a
h
A
作法:
1.作BC=a;
2.作线段BC的垂直平分线MN交BC于D点;
3.以D为圆心,h长为半径作弧交MN于A点;
4.连接AB,AC.
△ABC就是所求作的三角形.
典例精析
1.已知直线l和其上一点P,利用尺规作 l 的垂线,使它经过点P.
P
●
l
试一试
A
B
C
P
已知:直线 l 和 l 上一点P.
求作:PC⊥ l .
作法:
1.以点P为圆心,以任意长为半径作弧,与直线 l 相交于点A和B.
2.作线段AB的垂直平分线PC.
直线PC就是所求 l 的垂线.
l
B
A
作法:
2.已知直线 l 和线外一点P,利用尺规作 l 的垂线,使它经过点P.
(1)先以P为圆心,大于点P到直线 l 的垂直距离R为半径作圆,交直线 l 于A,B.
(2)分别以A、B为圆心,大于R的长
为半径作圆,相交于C、D两点.
(3)过两交点作直线 l ',此直线为
l 过P的垂线.
P ●
C
D
当堂练习
1.如图,等腰△ABC中,AB=AC,∠A=20°.线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于( )
A.80° B.70°
C.60° D.50°
C
B
A
D
E
C
2.下列说法错误的是 ( )
A.三角形三条边的垂直平分线必交于一点
B.如果等腰三角形内一点到底边两端点的距离相等,那么过这点与顶点的直线必垂直于底边
C.平面上只存在一点到已知三角形三个顶点距离相等
D.三角形关于任一边上的垂直平分线成轴对称
D
【解析】选D.等边三角形关于任一边上的垂直平分线成轴对称,等腰三角形关于底边上的垂直平分线成轴对称,一般三角形不是轴对称图形,D选项没有说明三角形的形状,所以D选项说法错误.
3.如图所示,在△ABC中,∠B=22.5°,AB的垂直平分线交BC于点D,DF⊥AC于点F,并与BC边上的高AE交于G.
求证:EG=EC.
F
A
B
C
E
G
D
证明:连接AD.∵点D在线段AB的垂直平分线上,
∴DA=DB,∴∠DAB=∠B=22.5°,
∴∠ADE=∠DAB+∠B=45°.
∵AE⊥BC,∴∠DAE=∠ADE=45°,
∴AE=DE.又∵DF⊥AC,
∴∠DFC=∠AEC=90°,
∴∠C+∠CAE=∠C+∠CDF=90°,
∴∠CAE=∠CDF,
∴△DEG≌△AEC(ASA),
∴EG=EC.
F
A
B
C
E
G
D
4.已知:线段a.
求作:△ABC,使∠ACB=90°,AC=BC=a.
作法:
(1)作直线l.
(2)在直线l上任取一条线段DE.
(3)作线段DE的垂直平分线MN交DE于C.
(4)在射线CE上截取CA=a,
在射线CM上截取CB=a.
(5)连接AB.
△ABC就是所求作的三角形.
课堂小结
1.定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
2.已知等腰三角形的底边和底边上的高作等腰三角形.
A
B
C
P
a
b
c
1.3 线段的垂直平分线
第一章 三角形的证明
导入新课
讲授新课
当堂练习
课堂小结
第2课时 三角形三边的垂直平分线及作图
1.理解并掌握三角形三边的垂直平分线的性质,能
够运用其解决实际问题.(重点)
2.能够利用尺规作出三角形的垂直平分线.
学习目标
导入新课
复习引入
A
B
C
D
1.回顾一下线段的垂直平分线的性质定理和判定定理.
2.线段的垂直平分线的作法.
性质:线段垂直平分线上的点到线段两端的距离相等.
判定:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
讲授新课
三角形三边的垂直平分线的性质
一
合作探究
画一画:利用尺规作三角形三条边的垂直平分线,完成之后你发现了什么?
发现:三角形三边的垂直平分线交于一点.这一点到三角形三个顶点的距离相等.
怎样证明这个结论呢
点拨:要证明三条直线相交于一点,只要证明其中两条直线的交点在第三条直线上即可.
思路可表示如下:
试试看,你会写出证明过程吗?
B
C
A
P
l
n
m
l是AB的垂直平分线
m是BC的垂直平分线
PA=PB
PB=PC
PA=PC
点P在AC的垂直平分线上
证明:连接PA,PB,PC.
∵点P在AB,AC的垂直平分线上, ∴PA=PB,PA=PC
(线段垂直平分线上 的点到线段两端距离相等).
∴PB=PC.
∴点P在BC的垂直平分线上
(到线段两端距离相等的点在线段的垂直平分线上).
B
C
A
P
l
n
m
定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
归纳总结
应用格式:
∵ 点P 为△ABC 三边垂直平分线的交点,
∴ PA =PB=PC.
A
B
C
P
分别作出锐角三角形、直角三角形、钝角三角形三边的垂直平分线,说明交点分别在什么位置.
锐角三角形三边的垂直平分线交点在三角形内;
直角三角形三边的垂直平分线交点在斜边上;
钝角三角形三边的垂直平分线交点在三角形外.
做一做
尺规作图
二
做一做:(1)已知三角形的一条边及这条边上的高,你能作出三角形吗 如果能,能作几个 所作出的三角形都全等吗
已知:三角形的一条边a和这边上的高h.
求作:△ABC,使BC=a,BC边上的高为h.
A1
D
C
B
A
a
h
(D)
C
B
A
a
h
A1
D
C
B
A
a
h
A1
提示:能作出无数个这样的三角形,它们并不全等.
(2)已知等腰三角形的底边,你能用尺规作出等腰三角形吗 如果能,能作几个 所作出的三角形都全等吗
这样的等腰三角形有无数多个.根据线段垂直平分线上的点到线段两个端点的距离相等,只要作底边的垂直平分线,取它上面除底边的中点外的任意一点,和底边的两个端点相连接,都可以得到一个等腰三角形.
如图所示,这些三角形不都全等.
(3)已知等腰三角形的底及底边上的高,你能用尺规作出等腰三角形吗?能作几个?
这样的等腰三角形只有两个,并且它们是全等的,分别位于已知底边的两侧.
例 已知:线段a,h.
求作:△ABC,使AB=AC,BC=a,高AD=h.
N
M
D
C
B
a
h
A
作法:
1.作BC=a;
2.作线段BC的垂直平分线MN交BC于D点;
3.以D为圆心,h长为半径作弧交MN于A点;
4.连接AB,AC.
△ABC就是所求作的三角形.
典例精析
1.已知直线l和其上一点P,利用尺规作 l 的垂线,使它经过点P.
P
●
l
试一试
A
B
C
P
已知:直线 l 和 l 上一点P.
求作:PC⊥ l .
作法:
1.以点P为圆心,以任意长为半径作弧,与直线 l 相交于点A和B.
2.作线段AB的垂直平分线PC.
直线PC就是所求 l 的垂线.
l
B
A
作法:
2.已知直线 l 和线外一点P,利用尺规作 l 的垂线,使它经过点P.
(1)先以P为圆心,大于点P到直线 l 的垂直距离R为半径作圆,交直线 l 于A,B.
(2)分别以A、B为圆心,大于R的长
为半径作圆,相交于C、D两点.
(3)过两交点作直线 l ',此直线为
l 过P的垂线.
P ●
C
D
当堂练习
1.如图,等腰△ABC中,AB=AC,∠A=20°.线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于( )
A.80° B.70°
C.60° D.50°
C
B
A
D
E
C
2.下列说法错误的是 ( )
A.三角形三条边的垂直平分线必交于一点
B.如果等腰三角形内一点到底边两端点的距离相等,那么过这点与顶点的直线必垂直于底边
C.平面上只存在一点到已知三角形三个顶点距离相等
D.三角形关于任一边上的垂直平分线成轴对称
D
【解析】选D.等边三角形关于任一边上的垂直平分线成轴对称,等腰三角形关于底边上的垂直平分线成轴对称,一般三角形不是轴对称图形,D选项没有说明三角形的形状,所以D选项说法错误.
3.如图所示,在△ABC中,∠B=22.5°,AB的垂直平分线交BC于点D,DF⊥AC于点F,并与BC边上的高AE交于G.
求证:EG=EC.
F
A
B
C
E
G
D
证明:连接AD.∵点D在线段AB的垂直平分线上,
∴DA=DB,∴∠DAB=∠B=22.5°,
∴∠ADE=∠DAB+∠B=45°.
∵AE⊥BC,∴∠DAE=∠ADE=45°,
∴AE=DE.又∵DF⊥AC,
∴∠DFC=∠AEC=90°,
∴∠C+∠CAE=∠C+∠CDF=90°,
∴∠CAE=∠CDF,
∴△DEG≌△AEC(ASA),
∴EG=EC.
F
A
B
C
E
G
D
4.已知:线段a.
求作:△ABC,使∠ACB=90°,AC=BC=a.
作法:
(1)作直线l.
(2)在直线l上任取一条线段DE.
(3)作线段DE的垂直平分线MN交DE于C.
(4)在射线CE上截取CA=a,
在射线CM上截取CB=a.
(5)连接AB.
△ABC就是所求作的三角形.
课堂小结
1.定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
2.已知等腰三角形的底边和底边上的高作等腰三角形.
A
B
C
P
a
b
c
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
