八年级下册:2.6.2-一元一次不等式组的解法(2)及应用 课件
文档属性
| 名称 | 八年级下册:2.6.2-一元一次不等式组的解法(2)及应用 课件 |

|
|
| 格式 | ppt | ||
| 文件大小 | 282.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-14 17:46:24 | ||
图片预览



文档简介
(共10张PPT)
2.6 一元一次不等式组
导入新课
讲授新课
当堂练习
课堂小结
第2课时 一元一次不等式组的解法(2)
及应用
1.解较复杂的一元一次不等式组;(重点、难点)
2.一元一次不等式组的实际应用.(难点)
学习目标
导入新课
问题:在什么条件下,长度为3cm , 7cm , xcm的三条线段可以围成一个三角形
所以,x的取值范围为4复习引入
利用三角形三边关系可知:
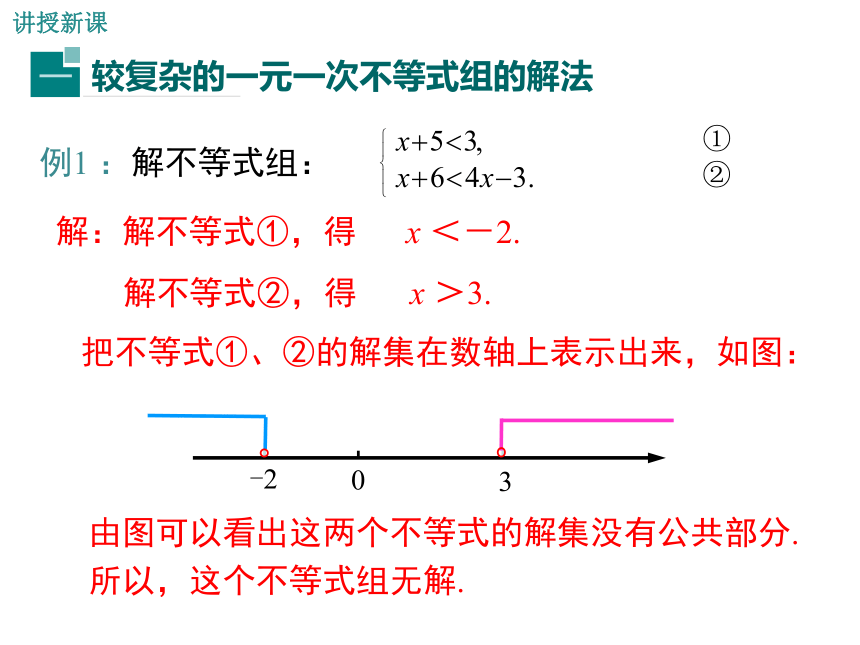
例1 :解不等式组:
解:解不等式①,得
x <-2.
解不等式②,得
x >3.
①
②
把不等式①、②的解集在数轴上表示出来,如图:
由图可以看出这两个不等式的解集没有公共部分.
所以,这个不等式组无解.
0
-2
3
较复杂的一元一次不等式组的解法
一
讲授新课
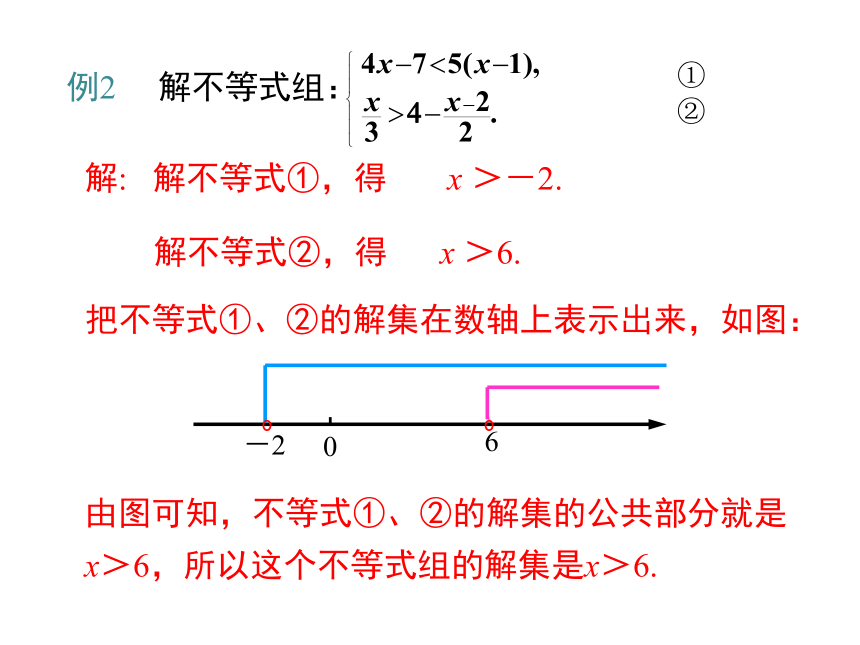
例2 解不等式组:
①
②
解: 解不等式①,得
x >-2.
解不等式②,得
x >6.
把不等式①、②的解集在数轴上表示出来,如图:
0
-2
6
由图可知,不等式①、②的解集的公共部分就是x>6,所以这个不等式组的解集是x>6.
例3 已知不等式组 的解集为-1<x<1,
则(a+1)(b-1)的值为多少
2x—a<1
x—2b>3
解: 由不等式组得:
x <
x >3+2b
因为不等式组的解集为: -1< x < 1 ,
所以,
=1
3a+2b= -1
解得
所以 (a+1)(b-1)=2×(-3)=-6.
b= -2
a= 1
因为x只能取整数,所以x=6,即有6辆汽车运这批货物.
例4 用若干辆载重量为 8 t 的汽车运一批货物,若每辆汽车只装 4 t ,则剩下 20 t 货物;若每辆汽车装满 8 t,则最后一辆汽车不满也不空.请你算一算:有多少辆汽车运这批货物?
解:设有x 辆汽车,则这批货物共有(4x+20 )t.依题意得
解不等式组,得5<x <7.
一元一次不等式组的应用
二
1.解下列不等式组:
解:(1) 1<x<5;
(2)-4<x≤1;
当堂练习
2.某校今年冬季烧煤取暖时间为4个月.如果每月比计划多烧5吨煤,那么取暖用煤量将超过100吨;如果每月比计划少烧5吨煤,呢么取暖用煤总量不足68吨.若设该校计划每月烧煤 x 吨,求x的取值范围.
解:根据题意,得
4(x+5)>100, ①
4(x-5)<68. ②
解不等式②,得
x <22.
解不等式①,得
x >20.
因此,原不等式组的解集为 20<x <22.
一元一次不等式组
课堂小结
利用公共部分确定不等式组的解集
分步解不等式
去括号、去分母
解较复杂的一元一次不等式组
→
实际应用(整数解)
→
2.6 一元一次不等式组
导入新课
讲授新课
当堂练习
课堂小结
第2课时 一元一次不等式组的解法(2)
及应用
1.解较复杂的一元一次不等式组;(重点、难点)
2.一元一次不等式组的实际应用.(难点)
学习目标
导入新课
问题:在什么条件下,长度为3cm , 7cm , xcm的三条线段可以围成一个三角形
所以,x的取值范围为4
利用三角形三边关系可知:
例1 :解不等式组:
解:解不等式①,得
x <-2.
解不等式②,得
x >3.
①
②
把不等式①、②的解集在数轴上表示出来,如图:
由图可以看出这两个不等式的解集没有公共部分.
所以,这个不等式组无解.
0
-2
3
较复杂的一元一次不等式组的解法
一
讲授新课
例2 解不等式组:
①
②
解: 解不等式①,得
x >-2.
解不等式②,得
x >6.
把不等式①、②的解集在数轴上表示出来,如图:
0
-2
6
由图可知,不等式①、②的解集的公共部分就是x>6,所以这个不等式组的解集是x>6.
例3 已知不等式组 的解集为-1<x<1,
则(a+1)(b-1)的值为多少
2x—a<1
x—2b>3
解: 由不等式组得:
x <
x >3+2b
因为不等式组的解集为: -1< x < 1 ,
所以,
=1
3a+2b= -1
解得
所以 (a+1)(b-1)=2×(-3)=-6.
b= -2
a= 1
因为x只能取整数,所以x=6,即有6辆汽车运这批货物.
例4 用若干辆载重量为 8 t 的汽车运一批货物,若每辆汽车只装 4 t ,则剩下 20 t 货物;若每辆汽车装满 8 t,则最后一辆汽车不满也不空.请你算一算:有多少辆汽车运这批货物?
解:设有x 辆汽车,则这批货物共有(4x+20 )t.依题意得
解不等式组,得5<x <7.
一元一次不等式组的应用
二
1.解下列不等式组:
解:(1) 1<x<5;
(2)-4<x≤1;
当堂练习
2.某校今年冬季烧煤取暖时间为4个月.如果每月比计划多烧5吨煤,那么取暖用煤量将超过100吨;如果每月比计划少烧5吨煤,呢么取暖用煤总量不足68吨.若设该校计划每月烧煤 x 吨,求x的取值范围.
解:根据题意,得
4(x+5)>100, ①
4(x-5)<68. ②
解不等式②,得
x <22.
解不等式①,得
x >20.
因此,原不等式组的解集为 20<x <22.
一元一次不等式组
课堂小结
利用公共部分确定不等式组的解集
分步解不等式
去括号、去分母
解较复杂的一元一次不等式组
→
实际应用(整数解)
→
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
