2.5.1一元一次不等式与一次函数

(共18张PPT)
（2007年潍坊市）幼儿园把新购进的一批玩具分给小朋友．若每人3件，那么还剩余59件；若每人5件，那么最后一个小朋友分到玩具，但不足4件，这批玩具共有 件．
昨日思考题
2.5.1一元一次不等式与一次函数
深圳罗湖外语实验学校 郑常娟
2.5.1一元一次不等式与一次函数
知识点：
1.通过观察一次函数的图象求出相应的一元一次方程的解、一元一次不等式的解集.
2.通过一元一次不等式与一次函数的图象之间的结合，培养数形结合意识.
知识回顾
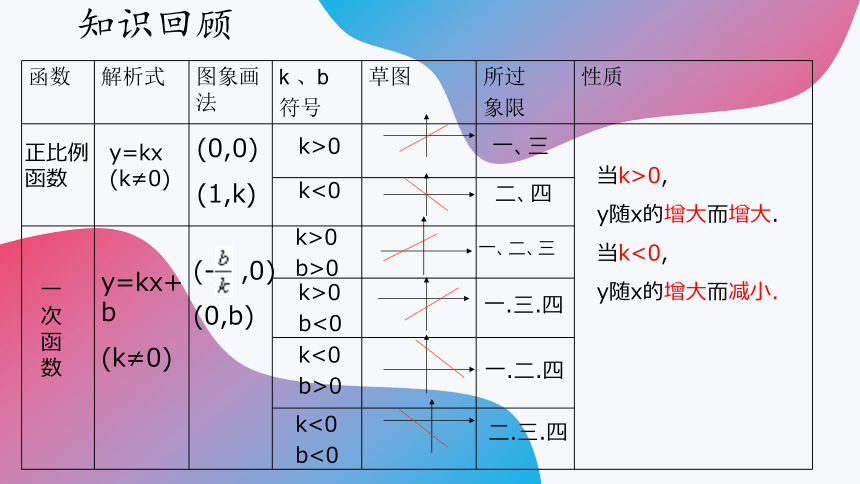
函数 解析式 图象画法 k 、b 符号 草图 所过 象限 性质
k<0
b>0
k<0
b<0
y=kx+b
(k≠0)
正比例函数
一次函数
k>0
y=kx (k≠0)
k<0
k>0
b>0
k>0
b<0
(0,0)
(1,k)
(- ,0)
(0,b)
一.二.四
二.三.四
当k>0,
y随x的增大而增大.
当k<0,
y随x的增大而减小.
一、三
二、四
一、二、三
一.三.四
知识回顾
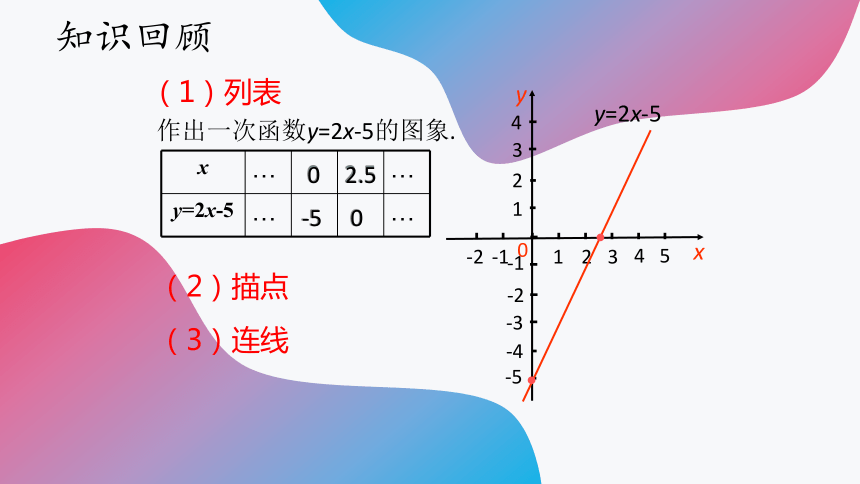
作出一次函数y=2x-5的图象.
0
1
2
3
4
5
-2
-1
x
2
-1
3
1
4
-3
-5
-2
-4
y
x … …
y=2x-5 … …
0
-5
2.5
0
y=2x-5
（2）描点
（3）连线
（1）列表
0
x
-1
1
y
2
3
1
4
3
2
-2
-3
-4
-5
-6
-1
P50例题：函数y=2x-5的图象如图,观察图象并回答问题：
（1）当x取何值时，2x-5=0
（2）当x取哪些值时，2x-5>0
解：当 x = 2.5 时， 2x-5=0.
解：当 x > 2.5 时， 2x-5>0.
(2.5,0)
y=2x-5
分析:
y=0
分析:
y>0
新知探究
0
x
-1
1
y
2
3
1
4
3
2
-2
-3
-4
-5
-6
-1
函数y=2x-5的图象如图,观察图象并回答问题：
（3）当x取哪些值时，2x-5<0
（4）当x取哪些值时，2x-5>1
新知探究
解：当 x < 2.5时， 2x-5<0.
(2.5,0)
（3,1）
解：当 x > 3时， 2x-5>1.
y=2x-5
分析:
y＜0
分析:
y > 1
0
x
-1
1
y
2
3
1
4
3
2
-2
-3
-4
-5
-6
-1
函数y=2x-5的图象如图,观察图象并回答问题：
（1）当x取何值时，2x-5=0
（2）当x取何值时，2x-5>0
（3）当x取何值时，2x-5<0
(2.5,0)
y=2x-5
观图象
找界点
分左右
定范围
新知探究
利用一次函数图像解决一元一次不等式问题
问题1：
作出函数y=2x-5的图象，观察图象回答下列问题：
(1) x取何值时，2x-5=0？
(2) x取哪些值时, 2x-5>0？
(3) x取哪些值时, 2x-5<0
(4) x取哪些值时, 2x-5>3
思考
能否将下述 “关于函数值的问题 ”,
改为 “关于x 的不等式的问题” ？
在一次函数 中，
当 时，可得一元一次方程 .
当 时，可得一元一次不等式 .
当 时，可得一元一次不等式 .
列式计算解法
用直接解不等式的方法求上题中的三个
不等式的解集，并比较两种方法的结果相同吗？
由上述讨论易知：
函数、(方程) 不等式
“关于一次函数的值的问题”
可变换成 “关于一次不等式的问题” ；
反过来， “关于一次不等式的问题”
可变换成 “关于一次函数的值的问题”。
因此，
我们既可以运用函数图象解不等式 ，
也可以运用解不等式帮助研究函数问题 ，
二者相互渗透 ，互相作用。
数形结合思想
想一想：
1、如果y=-2x-5,
那么当x取何
值时，y>0
1
2
3
4
-1
-2
-3
-1
-2
-3
-4
0
1
2
3
4
x
-5
y
y=-2x-5
解：由图可知，当x<-2.5时,y>0
y
y
y
-2.5
2020/9/26
2、若y1=-x+3,y2=3x-4,试确定当x取何值时
（1）y1＜y2？
（2）y1=y2？
（3）y1>y2？
当x＞ 　时，y1＜y2
当x=　　时，y1=y2
当x＜　　时，y1>y2
3、如图，直线y1=x+b与y2=kx-1相交于点P，若P的横坐标为-1，则关于x的不等式x+b＞kx-1的解集是（　　）
A. x≥-1 B. x＞-1
C. x≤-1 D. x＜-1
解：由图像可知，
当x＞-1时，x+b＞kx-1，
即不等式x+b＞kx-1的解集为x＞-1．
故选B．
B
4、兄弟俩赛跑，哥哥先让弟弟9m，然后自己才开始跑，已知弟弟每秒跑3m，哥哥每秒4m，列出函数关系式，画出函数图象，观察图象回答下列问题：
（1）何时弟弟跑在哥哥前面？
（2）何时哥哥跑在弟弟前面？
（3）谁先跑过20m？谁先跑过100m？
（4）你是怎样求解的？与同伴交流。
答案：
y1=4x，y2=9+3x.
（1）9秒前弟弟在哥哥前。
（2）9秒后哥哥跑在弟弟前。
（3）弟弟先跑过20m处，
哥哥先跑过100m处。
（4）除了运用图象法解之外，
还可直接用不等式求解。
（9，*）
5、甲、乙两辆摩托车从相距20km的A、B两地相向而行，图中l1、l2分别表示两辆摩托车离开A地的距离s（km）与行驶时间t（h）之间函数关系。
（1）哪辆摩托车的速度较快？
（2）经过多长时间，甲车行驶到A、B两地中点？
解答：（1）从图象中可知
故摩托车乙速度快。
（2）当s=10km时，
即经过0.3h时，甲车行驶到A、B两地的中点。
1、一次函数(值)的变化对应着相应自变量的取值范围,
这个取值范围, 既可从一次函数的图象上直观看出(近似值),
也可通过解(方程)不等式而得到(精确值).
2、“一次函数问题”可转换成 “一次不等式的问题” ；
反过来，“一次不等式的问题”可转换成 “一次函数的问题”。
我们既可以运用函数图象解不等式 ，也可以运用解不等式帮助研究函数问题 ，二者相互渗透 ，互相作用。
不等式与 函数 、方程 是紧密联系着的一个整体 。
课堂小结
2、课堂笔记今天下午6点之前拍照上传科代表实时打卡，作为上课表现评判标准之一。
3、写好本堂课日期、名称；做好本节课全部笔记和课堂练习；书写认真清晰；课堂练习要求要用红笔订正。
作业要求（注意按照“作业要求”完成作业）
新课标38页基础训练1，2，3，4，5.
1、 今晚10：00前完成作业，拍高清照上传到作业登记本