4.2.1提取公因式(八年级下册)深圳市桂园中学黄诗蕴
文档属性
| 名称 | 4.2.1提取公因式(八年级下册)深圳市桂园中学黄诗蕴 |

|
|
| 格式 | pptx | ||
| 文件大小 | 831.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-14 18:01:56 | ||
图片预览








文档简介
(共29张PPT)
授课老师:深圳市桂园中学黄诗蕴
§4.2.1提取公因式
北师大版八年级下册
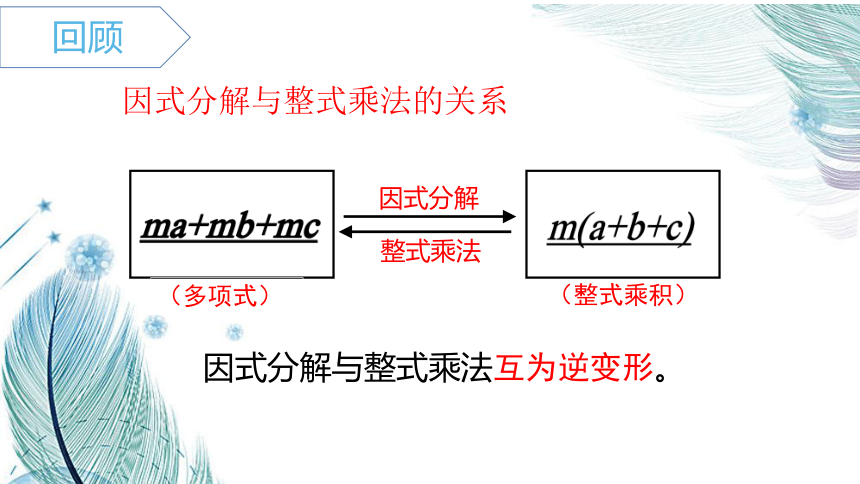
因式分解
整式乘法
(多项式)
(整式乘积)
因式分解与整式乘法互为逆变形。
因式分解与整式乘法的关系
回顾
问题一:什么是公因式
观察下列各式的结构,有什么共同特点?
各项中都含有一个公共的因式
如果一个多项式中各项都含有一个公共的因式,则我们把这个因式叫做这个多项式的公因式。
尝试探究
例: 找 2 x 2 + 6 x 的公因式。
定系数
2
定字母
x
定指数
2
3
所以,公因式是 2 x
2
思考
怎样确定多项式的公因式?
多项式中各项都含有的相同因式,叫做这个多项式各项的公因式。
系数:找各项的最大公约数。
字母:找各项的相同字母
指数:找相同字母的最低次幂
多项式的公因式
如何确定公因式?
归纳
1. 在横线上写出下列各多项式的公因式:
(1)x2-5xy:_________;
(2)-3m2+12mn:__________;
(3)12b3-8b2+4b:__________;
(4)-4a3b2-12ab3:__________;
(5)-x3y3+x2y2+2xy:__________;
(6)8x3y2-12xy3:__________.
x
-3m
4b
-4ab2
-xy
4xy2
练一练
注意:各项系数都是整数时,因式的系数应取各项系数的最大公约数;字母取各项的相同的字母,而且各字母的指数取次数最低的.
如果多项式的各项有公因式,那么可以把这个公因式提到括号外面,将多项式写成因式乘积的形式,这种分解因式的方法,叫做提取公因式。
探索新知
例1:把 3a2-9ab分解因式.
温馨提示
分两步
第一步,找出公因式;
第二步,提取公因式 ,
(即将多项式化为两个因式的乘积)
解:原式 =3a a-3a 3b
=3a(a-3b)
例题讲解
例2 把 9x2– 6xy+3xz 分解因式.
=
3x·3x - 3x·2y +3x·z
解:
=
3x (3x-2y+z)
9x2 – 6 x y + 3x z
例题讲解
练一练:把下列各式因式分解
巩固练习
提公因式法分解因式
正确的找出多项式各项的公因式。
注意:
1 多项式是几项,提公因式后也剩几项。
2 当多项式的某一项和公因式相同时提公因式后剩余的项是1。
3、当多项式第一项系数是负数,通常先提出“-”号,使括号内第一项系数变为正数,注意括号内各项都要变号。
归纳
.把下列各式分解因式:
解:原式=-(a2-ab+ac)
=-a(a-b+c);
解:原式=-(2x3-6x2+2x)
=-2x(x2-3x+1).
巩固练习
判断下列因式分解是否正确
1.4a2b- 6ab2+ 2ab=2ab(2a–3b)
2.6(a-b)2–12(a-b)= 2(a-b)(3a-3b-6)
正解: 4a2b- 6ab2+ 2ab=2ab(2a–3b+1)
正解: 6(a-b)2–12(a-b)= 6(a-b) (a-b-2)
x(x+y)2–x(x+y)(x–y)= x(x+y)[(x+y)–(x–y)]
正解: x(x+y)2–x(x+y)(x–y)
= x(x+y)[(x+y)–(x–y)]
= x(x+y)(x+y–x+y)
=2xy(x+y)
巩固练习
课本P96,习题4.2,第1题
看你能否过关?
巩固练习
巩固练习
【例5】已知a+b=2,ab=2,求a2b+ab2的值.
解:∵a+b=2,ab=2,
∴a2b+ab2
=ab(a+b)
=2×2
=4.
新知应用
练一练:
已知x+2y+4=0,xy=3,求-6x2y-12xy2的值.
解:由x+2y+4=0,得x+2y=-4.
∴-6x2y-12xy2
=-6xy(x+2y)
=-6×3×(-4)
=72.
巩固练习
1.若x+y=1,xy=﹣7,则x2y+xy2= .
解:∵x+y=1,xy=﹣7,
∴原式=xy(x+y)=﹣7, 故答案为:﹣7
2.已知:x2+3x+2=0,则5x1000+15x999+10x998= .
解:5x1000+15x999+10x998=5x998(x2+3x+2),
∵x2+3x+2=0,
∴原式=0.故答案为0.
-7
0
3.如果x+y=5,xy=﹣3,则x2y+xy2= ,x2+y2=______
解:∵x+y=5,xy=﹣3,
∴x2y+xy2=xy(x+y)=﹣3×5=﹣15,
x2+y2=(x+y)2﹣2xy=52﹣2×(﹣3)=31.故答案为:﹣15,31.
4.若a,b互为相反数,则a(x﹣3y)﹣b(3y﹣x)的值为 .
解:∵a,b互为相反数,
∴a+b=0,
∴a(x﹣3y)﹣b(3y﹣x)=a(x﹣3y)+b(x﹣3y)=(x﹣3y)(a+b)=0.
巩固练习
-15
31
0
.先阅读下列因式分解的过程,再回答所提出的问题:
例1、1+x+x(1+x) 例2、1+x+x(1+x)+x(1+x)2
=(1+x)(1+x) =(1+x)(1+x)+x(1+x)2
=(1+x)2 =(1+x)2+x(1+x)2
=(1+x)2(1+x)
=(1+x)3
(1)分解因式:
1+x+x(1+x)+x(1+x)2+x(1+x)3= ______;
1+x+x(1+x)+x(1+x)2+x(1+x)3+x(1+x)4= _____;
1+x+x(1+x)+x(1+x)2+…+x(1+x)n= ______.
(1+x)4
(1+x)5
(1+x)n+1
.先阅读下列因式分解的过程,再回答所提出的问题:
例1、1+x+x(1+x) 例2、1+x+x(1+x)+x(1+x)2
=(1+x)(1+x) =(1+x)(1+x)+x(1+x)2
=(1+x)2 =(1+x)2+x(1+x)2
=(1+x)2(1+x)
=(1+x)3
(2)分解因式:(要求写出关键步骤)
x﹣1﹣x(x﹣1)+x(x﹣1)2﹣x(x﹣1)3+x(x﹣1)4.
(2)x﹣1﹣x(x﹣1)+x(x﹣1)2﹣x(x﹣1)3+x(x﹣1)4
=(x﹣1)﹣x(x﹣1)+x(x﹣1)2﹣x(x﹣1)3+x(x﹣1)4
=﹣(x﹣1)(x﹣1)+x(x﹣1)2﹣x(x﹣1)3+x(x﹣1)4
=(x﹣1)2(﹣1+x)﹣x(x﹣1)3+x(x﹣1)4
=(x﹣1)3(1﹣x)+x(x﹣1)4
=(x﹣1)4(x﹣1)
=(x﹣1)5.
2、确定公因式的方法:
小结与反思
3、用提公因式法分解因式的步骤:
1、什么叫公因式、提公因式法?
4、用提公因式法分解因式应注意的问题:
(1)公因式要提尽;
(2)小心漏项;
(3)首项为负与众不同。
第一步,找出公因式; 第二步,提公因式; 第三步,把多项式化成两个因式乘积的形式。
1)定系数 2)定字母 3)定指数
:
=--
答:能被45整除
布置作业:练习册
谢谢观看
授课教师:深圳市桂园中学黄诗蕴
授课老师:深圳市桂园中学黄诗蕴
§4.2.1提取公因式
北师大版八年级下册
因式分解
整式乘法
(多项式)
(整式乘积)
因式分解与整式乘法互为逆变形。
因式分解与整式乘法的关系
回顾
问题一:什么是公因式
观察下列各式的结构,有什么共同特点?
各项中都含有一个公共的因式
如果一个多项式中各项都含有一个公共的因式,则我们把这个因式叫做这个多项式的公因式。
尝试探究
例: 找 2 x 2 + 6 x 的公因式。
定系数
2
定字母
x
定指数
2
3
所以,公因式是 2 x
2
思考
怎样确定多项式的公因式?
多项式中各项都含有的相同因式,叫做这个多项式各项的公因式。
系数:找各项的最大公约数。
字母:找各项的相同字母
指数:找相同字母的最低次幂
多项式的公因式
如何确定公因式?
归纳
1. 在横线上写出下列各多项式的公因式:
(1)x2-5xy:_________;
(2)-3m2+12mn:__________;
(3)12b3-8b2+4b:__________;
(4)-4a3b2-12ab3:__________;
(5)-x3y3+x2y2+2xy:__________;
(6)8x3y2-12xy3:__________.
x
-3m
4b
-4ab2
-xy
4xy2
练一练
注意:各项系数都是整数时,因式的系数应取各项系数的最大公约数;字母取各项的相同的字母,而且各字母的指数取次数最低的.
如果多项式的各项有公因式,那么可以把这个公因式提到括号外面,将多项式写成因式乘积的形式,这种分解因式的方法,叫做提取公因式。
探索新知
例1:把 3a2-9ab分解因式.
温馨提示
分两步
第一步,找出公因式;
第二步,提取公因式 ,
(即将多项式化为两个因式的乘积)
解:原式 =3a a-3a 3b
=3a(a-3b)
例题讲解
例2 把 9x2– 6xy+3xz 分解因式.
=
3x·3x - 3x·2y +3x·z
解:
=
3x (3x-2y+z)
9x2 – 6 x y + 3x z
例题讲解
练一练:把下列各式因式分解
巩固练习
提公因式法分解因式
正确的找出多项式各项的公因式。
注意:
1 多项式是几项,提公因式后也剩几项。
2 当多项式的某一项和公因式相同时提公因式后剩余的项是1。
3、当多项式第一项系数是负数,通常先提出“-”号,使括号内第一项系数变为正数,注意括号内各项都要变号。
归纳
.把下列各式分解因式:
解:原式=-(a2-ab+ac)
=-a(a-b+c);
解:原式=-(2x3-6x2+2x)
=-2x(x2-3x+1).
巩固练习
判断下列因式分解是否正确
1.4a2b- 6ab2+ 2ab=2ab(2a–3b)
2.6(a-b)2–12(a-b)= 2(a-b)(3a-3b-6)
正解: 4a2b- 6ab2+ 2ab=2ab(2a–3b+1)
正解: 6(a-b)2–12(a-b)= 6(a-b) (a-b-2)
x(x+y)2–x(x+y)(x–y)= x(x+y)[(x+y)–(x–y)]
正解: x(x+y)2–x(x+y)(x–y)
= x(x+y)[(x+y)–(x–y)]
= x(x+y)(x+y–x+y)
=2xy(x+y)
巩固练习
课本P96,习题4.2,第1题
看你能否过关?
巩固练习
巩固练习
【例5】已知a+b=2,ab=2,求a2b+ab2的值.
解:∵a+b=2,ab=2,
∴a2b+ab2
=ab(a+b)
=2×2
=4.
新知应用
练一练:
已知x+2y+4=0,xy=3,求-6x2y-12xy2的值.
解:由x+2y+4=0,得x+2y=-4.
∴-6x2y-12xy2
=-6xy(x+2y)
=-6×3×(-4)
=72.
巩固练习
1.若x+y=1,xy=﹣7,则x2y+xy2= .
解:∵x+y=1,xy=﹣7,
∴原式=xy(x+y)=﹣7, 故答案为:﹣7
2.已知:x2+3x+2=0,则5x1000+15x999+10x998= .
解:5x1000+15x999+10x998=5x998(x2+3x+2),
∵x2+3x+2=0,
∴原式=0.故答案为0.
-7
0
3.如果x+y=5,xy=﹣3,则x2y+xy2= ,x2+y2=______
解:∵x+y=5,xy=﹣3,
∴x2y+xy2=xy(x+y)=﹣3×5=﹣15,
x2+y2=(x+y)2﹣2xy=52﹣2×(﹣3)=31.故答案为:﹣15,31.
4.若a,b互为相反数,则a(x﹣3y)﹣b(3y﹣x)的值为 .
解:∵a,b互为相反数,
∴a+b=0,
∴a(x﹣3y)﹣b(3y﹣x)=a(x﹣3y)+b(x﹣3y)=(x﹣3y)(a+b)=0.
巩固练习
-15
31
0
.先阅读下列因式分解的过程,再回答所提出的问题:
例1、1+x+x(1+x) 例2、1+x+x(1+x)+x(1+x)2
=(1+x)(1+x) =(1+x)(1+x)+x(1+x)2
=(1+x)2 =(1+x)2+x(1+x)2
=(1+x)2(1+x)
=(1+x)3
(1)分解因式:
1+x+x(1+x)+x(1+x)2+x(1+x)3= ______;
1+x+x(1+x)+x(1+x)2+x(1+x)3+x(1+x)4= _____;
1+x+x(1+x)+x(1+x)2+…+x(1+x)n= ______.
(1+x)4
(1+x)5
(1+x)n+1
.先阅读下列因式分解的过程,再回答所提出的问题:
例1、1+x+x(1+x) 例2、1+x+x(1+x)+x(1+x)2
=(1+x)(1+x) =(1+x)(1+x)+x(1+x)2
=(1+x)2 =(1+x)2+x(1+x)2
=(1+x)2(1+x)
=(1+x)3
(2)分解因式:(要求写出关键步骤)
x﹣1﹣x(x﹣1)+x(x﹣1)2﹣x(x﹣1)3+x(x﹣1)4.
(2)x﹣1﹣x(x﹣1)+x(x﹣1)2﹣x(x﹣1)3+x(x﹣1)4
=(x﹣1)﹣x(x﹣1)+x(x﹣1)2﹣x(x﹣1)3+x(x﹣1)4
=﹣(x﹣1)(x﹣1)+x(x﹣1)2﹣x(x﹣1)3+x(x﹣1)4
=(x﹣1)2(﹣1+x)﹣x(x﹣1)3+x(x﹣1)4
=(x﹣1)3(1﹣x)+x(x﹣1)4
=(x﹣1)4(x﹣1)
=(x﹣1)5.
2、确定公因式的方法:
小结与反思
3、用提公因式法分解因式的步骤:
1、什么叫公因式、提公因式法?
4、用提公因式法分解因式应注意的问题:
(1)公因式要提尽;
(2)小心漏项;
(3)首项为负与众不同。
第一步,找出公因式; 第二步,提公因式; 第三步,把多项式化成两个因式乘积的形式。
1)定系数 2)定字母 3)定指数
:
=--
答:能被45整除
布置作业:练习册
谢谢观看
授课教师:深圳市桂园中学黄诗蕴
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
