刘珂珂说课《平面图形的镶嵌》

(共17张PPT)
《平面图形的镶嵌》
刘珂珂
八年级下册 综合与实践
学习目标
知识与技能：通过观察图片，发现特征，得出平面镶嵌的概念；
过程与方法：通过小组合作，探索用一种正多边形镶嵌平面的条件，并进一步运用到一般多边形或几种图形的平面图形镶嵌；
情感态度与价值观：经历观察、拼图、交流等活动，提高分析图形、合情推理的能力，培养审美情趣。
课前准备
基本图形的纸片：
三角形：正三角形、一般三角形
四边形：正方形、一般四边形
五边形：正五边形、一般五边形
六边形：正六边形、一般六边形
八边形：正八边形
课前导入
认真观察我们周围的事物，你会发现许多用各种材料拼接成的美丽图案。
小组讨论，这些拼接成的图案有什么共同特点？
新课讲授
探究一：平面图形的镶嵌的概念
这些拼接成的图案具有的特征：
完全相同的基本图形
不留空隙
不重叠
课本 P351
平面图形的镶嵌：
用形状、大小完全相同的一种或几种平面图形进行拼接，彼此之间不留空隙、不重叠地铺成一片，就是平面图形的镶嵌。
新课讲授
探究二：一种多边形的平面镶嵌
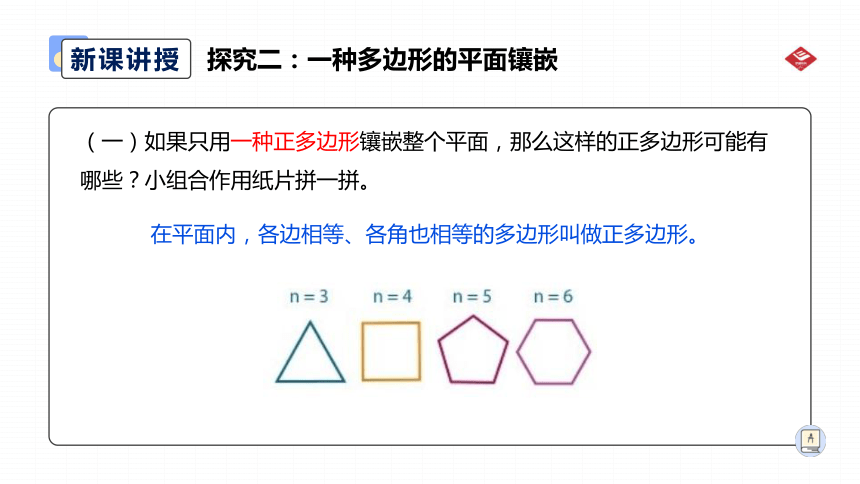
（一）如果只用一种正多边形镶嵌整个平面，那么这样的正多边形可能有哪些？小组合作用纸片拼一拼。
在平面内，各边相等、各角也相等的多边形叫做正多边形。
新课讲授
探究二：一种多边形的平面镶嵌
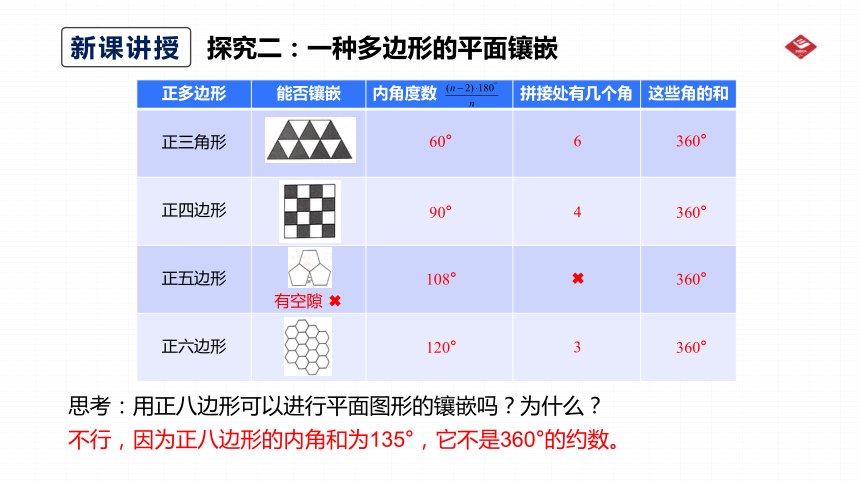
正多边形 能否镶嵌 内角度数 拼接处有几个角 这些角的和
正三角形
正四边形
正五边形
正六边形
有空隙
60°
90°
108°
120°
6
4

3
360°
360°
360°
360°
思考：用正八边形可以进行平面图形的镶嵌吗？为什么？
不行，因为正八边形的内角和为135°，它不是360°的约数。
新课讲授
探究二：一种多边形的平面镶嵌
归纳总结：
1、只用一种正多边形进行平面图形的镶嵌，这样的多边形有：正三角形、正四边形、正六边形。
2、能够进行平面镶嵌的根本原因：能拼成360°的角。
新课讲授
探究二：一种多边形的平面镶嵌
（二）在一般的多边形中，有哪些可以镶嵌整个平面？小组合作用纸片拼一拼。
一般三角形
一般四边形
一般五边形
一般六边形
可以
可以
有条件：比如3个内角相等，其余2个内角为90°
有条件
七边形及以上
不可以
新课讲授
探究三：两种多边形的平面镶嵌
如果用两种正多边形进行镶嵌，你能想到哪些？小组合作拼一拼。
正三角形+正四边形
正三角形+正六边形
正四边形+正八边形
新课讲授
探究三：两种多边形的平面镶嵌
通过探究我们知道，能够进行平面镶嵌的根本原因：能拼成360°的角。那你可以用一个方程来表示两种正多边形镶嵌背后的数量关系吗？
设：m个内角为ɑ的正多边形，n个内角为β的正多边形可以实现镶嵌，则
新课讲授
探究三：两种多边形的平面镶嵌
验证：正三角形与正六边形能够进行平面镶嵌。
设：在一个顶点周围有m个正三角形，n个正六边形的角，则
拓展延伸
探究四：不规则图形的平面镶嵌
（一）用如图所示的2种图形，能镶嵌整个平面吗？小组合作画一画。
可以，这两个曲边形能够补成一个正方形
拓展延伸
探究四：不规则图形的平面镶嵌
（二）用如图所示的2种图形，能镶嵌整个平面吗？将它们与平行四边形的镶嵌图案作比较，两者分别有什么关系？小组合作画一画。
可以，它们都可以看成由平行四边形切割组合而成
如果一个图形（如平行四边形）通过平移可以镶嵌平面，那么将这个图形上的一部分切割组合，仍然可以镶嵌平面。
课堂练习
一幅美丽的图案，在某个顶点处由四个边长相等的正多边形镶嵌而成，其中的三个分别为正三角形、正方形、正六边形，则另一个是（ ）
[答案] B
A.正三角形
C.正五边形
D．正六边形
B．正方形
解析：
能够进行平面镶嵌的根本原因：能拼成360°的角。正三角形内角为60°，正方形内角为90°，正六边形内角为120°，所以用360°- 60°- 90°- 120° = 90°
课堂小结
1、用形状、大小完全相同的一种或几种平面图形进行拼接，彼此之间不留空隙、不重叠地铺成一片，就是平面图形的镶嵌。
2、只用一种正多边形进行平面图形的镶嵌，这样的多边形有：正三角形、正四边形、正六边形。
3、能够进行平面镶嵌的根本原因：能拼成360°的角。
课后作业