平面图形的镶嵌-说课-翠园文锦中学-汤子弘
文档属性
| 名称 | 平面图形的镶嵌-说课-翠园文锦中学-汤子弘 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-14 18:01:56 | ||
图片预览





文档简介
(共16张PPT)
平面图形的镶嵌
深圳市文锦中学 - 汤子弘
教材分析
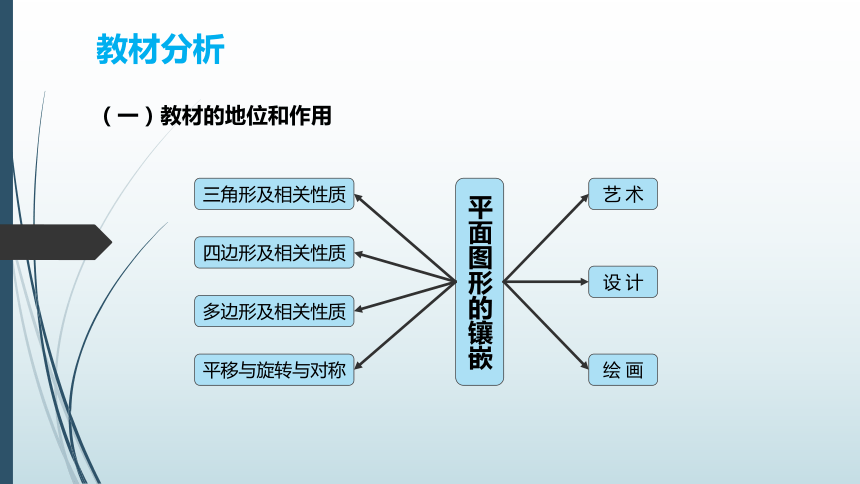
(一)教材的地位和作用
平面图形的镶嵌
三角形及相关性质
四边形及相关性质
多边形及相关性质
平移与旋转与对称
艺 术
绘 画
设 计
教材分析
(二)教学目标
1、知识与技能:通过探索平面图形的镶嵌,使学生了解平面图形镶嵌的概念。了解任意一个三角形、四边形或正六边形可以镶嵌平面图形。
2、过程与方法:经历探索的过程,发展学生的合作能力,增强推理能力,能运用这几种图形进行简单的平面图形镶嵌设计。
3、情感态度价值观:培养学生观察、动手操作能力,让学生进一步感受数学与生活的紧密联系。
教材分析
教学重点:
探索多边形镶嵌的条件的过程。
教学难点:
寻找多边形镶嵌的条并如何运用镶嵌的条件解决问题。
教法分析
讨论法、实验演示法
教师
学生
镶嵌的条件
注重引导
多元提问
小组探究
实践归纳
特殊
一般
探索规律
总结规律
理论
实践
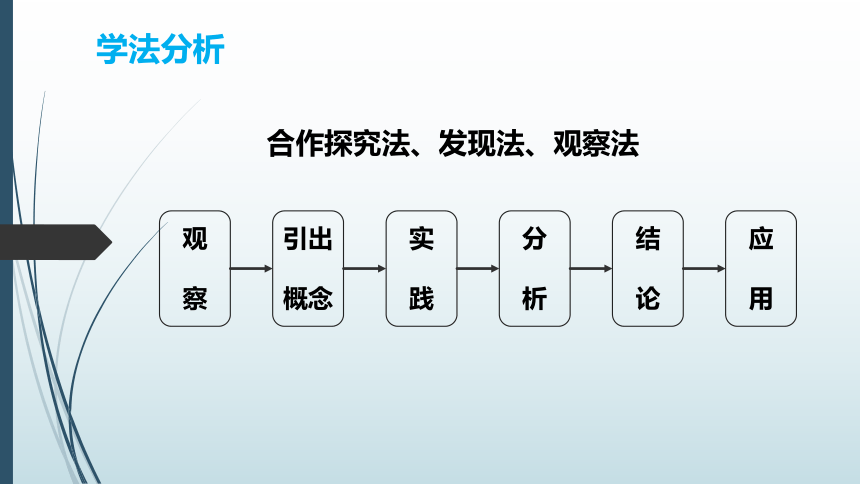
学法分析
观
察
引出
概念
实
践
分
析
结
论
应
用
合作探究法、发现法、观察法
教学过程
各环节时间安排:
环节一:依纲靠本独立研习——10分钟
环节二:分享交流互动引深——18分钟
环节三:小组分享互助研习——12分钟
环节四:巩固内化小组总结——5分钟
一、多观察
通过观察以上图案,在形状和大小方面分别有什么共同特征?这些图形在拼接时有什么特点?请同学们分组讨论、交流。
四边形
四边形
六边形
四边形
四边形
1、形状一样
2、大小一样
3、没有缝隙
密
铺
平面图形的镶嵌
二、动动手
以小组为单位,组内拿出课前准备的正三角形、正四边形、正五边形、正六边形的硬纸片拼接镶嵌图形,随后进行小组展示。(要求:密铺)
得出结论:
因为正六边形的每一个内角是 °,在每一个顶点处有 个正六边形, 分别有一个内角,它们彼此相邻,这三个内角的和是 °。正三角形、正方形密铺也满足以拼接点为顶点的各角之和为 °。
二、动动手
全等的正六边形能密铺,正六边形的每个内角是多少度?
在一个顶点处的三个正六边形,分别有一个内角,它们彼此相邻,这三个内角的和是多少度 正三角形、正方形呢
120
360
360
3
二、动动手
如果一种平面图形能密铺,那么这种图形的若干个内角和是 °。
正五边形的每个内角是 °;它的若干个内角的和能等于360°吗?那么全等的正五边形能密铺吗?
360
108
正多边形镶嵌的条件:以拼接点为顶点的各角之和为360°.
结论:
难道密铺一定要是同一种图形吗?
三、拼图竞赛
小组用准备好的不同多边形硬纸板密铺地面。不同的图形硬纸板能否实现密铺呢?按照什么样的方式能够密铺呢?
在3分钟内,以小组为单位进行密铺,最后由老师选出一名一等奖、两名二等奖、三名三等奖。
四、总结
密
铺
平面图形的镶嵌
正多边形镶嵌的条件:
以拼接点为顶点的各角之和为360°.
五、密铺的艺术
埃舍尔作品欣赏
五、密铺的艺术
埃舍尔作品欣赏
谢谢大家
平面图形的镶嵌
深圳市文锦中学 - 汤子弘
教材分析
(一)教材的地位和作用
平面图形的镶嵌
三角形及相关性质
四边形及相关性质
多边形及相关性质
平移与旋转与对称
艺 术
绘 画
设 计
教材分析
(二)教学目标
1、知识与技能:通过探索平面图形的镶嵌,使学生了解平面图形镶嵌的概念。了解任意一个三角形、四边形或正六边形可以镶嵌平面图形。
2、过程与方法:经历探索的过程,发展学生的合作能力,增强推理能力,能运用这几种图形进行简单的平面图形镶嵌设计。
3、情感态度价值观:培养学生观察、动手操作能力,让学生进一步感受数学与生活的紧密联系。
教材分析
教学重点:
探索多边形镶嵌的条件的过程。
教学难点:
寻找多边形镶嵌的条并如何运用镶嵌的条件解决问题。
教法分析
讨论法、实验演示法
教师
学生
镶嵌的条件
注重引导
多元提问
小组探究
实践归纳
特殊
一般
探索规律
总结规律
理论
实践
学法分析
观
察
引出
概念
实
践
分
析
结
论
应
用
合作探究法、发现法、观察法
教学过程
各环节时间安排:
环节一:依纲靠本独立研习——10分钟
环节二:分享交流互动引深——18分钟
环节三:小组分享互助研习——12分钟
环节四:巩固内化小组总结——5分钟
一、多观察
通过观察以上图案,在形状和大小方面分别有什么共同特征?这些图形在拼接时有什么特点?请同学们分组讨论、交流。
四边形
四边形
六边形
四边形
四边形
1、形状一样
2、大小一样
3、没有缝隙
密
铺
平面图形的镶嵌
二、动动手
以小组为单位,组内拿出课前准备的正三角形、正四边形、正五边形、正六边形的硬纸片拼接镶嵌图形,随后进行小组展示。(要求:密铺)
得出结论:
因为正六边形的每一个内角是 °,在每一个顶点处有 个正六边形, 分别有一个内角,它们彼此相邻,这三个内角的和是 °。正三角形、正方形密铺也满足以拼接点为顶点的各角之和为 °。
二、动动手
全等的正六边形能密铺,正六边形的每个内角是多少度?
在一个顶点处的三个正六边形,分别有一个内角,它们彼此相邻,这三个内角的和是多少度 正三角形、正方形呢
120
360
360
3
二、动动手
如果一种平面图形能密铺,那么这种图形的若干个内角和是 °。
正五边形的每个内角是 °;它的若干个内角的和能等于360°吗?那么全等的正五边形能密铺吗?
360
108
正多边形镶嵌的条件:以拼接点为顶点的各角之和为360°.
结论:
难道密铺一定要是同一种图形吗?
三、拼图竞赛
小组用准备好的不同多边形硬纸板密铺地面。不同的图形硬纸板能否实现密铺呢?按照什么样的方式能够密铺呢?
在3分钟内,以小组为单位进行密铺,最后由老师选出一名一等奖、两名二等奖、三名三等奖。
四、总结
密
铺
平面图形的镶嵌
正多边形镶嵌的条件:
以拼接点为顶点的各角之和为360°.
五、密铺的艺术
埃舍尔作品欣赏
五、密铺的艺术
埃舍尔作品欣赏
谢谢大家
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
