2.5 一元一次不等式与一次函数(2)
文档属性
| 名称 | 2.5 一元一次不等式与一次函数(2) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-14 18:01:56 | ||
图片预览








文档简介
(共26张PPT)
第二章 一元一次不等式与
一元一次不等式组
2.5 一元一次不等式与一次函数(二)
授课人:翠园初级中学 徐怡旭
1.利用一次函数、一元一次不等式及一元一次方程这
三者之间的关系解决生活中的实际问题.(重点、难点)
2.运用数形结合思想方便快捷解决问题.
学习目标
复习导入
一次函数与一元一次不等式
一
“解不等式ax+b>0(a,b为常数,a≠0)”与
“求自变量x在什么范围内,一次函数y=ax+b的值大于0”
这两个问题之间有什么关系?
这两个问题实际上是同一个问题.
由于任何一元一次不等式都可以转化为ax+b>0或ax+b<0(a、b为常数,a≠0)的形式,所以解一元一次不等式可以看作:当对应的一次函数值大于(或小于)0时,求自变量相应的取值范围。
问题情境
目前受疫情影响,学生只能在家网络学习.某偏远地区的郝同学因家中没有网络,只能选择用手机流量上课.某电信公司有两种手机流量收费业务.套餐一规定每月月租费10元,每使用1G流量收费2元;套餐二不收月租费,但每使用1G流量收费4元.你认为郝同学选择哪种套餐更合算?
一元一次不等式与一次函数的综合应用
一
解:设郝同学每月使用的流量为 x G,套餐一每个月的消费额为y1,套餐二每个月的消费额为y2,根据题意可知
y1=10+2x y2=4x
问题情境
一元一次不等式与一次函数的综合应用
一
当两种套餐消费额一样时,
即y1= y2,得10+2x=4x,
解得x=5;
y1=10+2x y2=4x
当两种套餐消费额不一样时,
①由y1>y2,得10+2x>4x,解得x<5;
此时选择套餐二比较合算.
②由y15.
此时选择套餐一比较合算.
目前受疫情影响,学生只能在家网络学习.某偏远地区的郝同学因家中没有网络,只能选择用手机流量上课.某电信公司有两种手机流量收费业务.套餐一规定每月月租费10元,每使用1G流量收费2元;套餐二不收月租费,但每使用1G流量收费4元.你认为郝同学选择哪种套餐更合算?
问题情境
一元一次不等式与一次函数的综合应用
一
所以当郝同学每个月使用的流量等于5G时,选择两种套餐一样合算;
如果每个月使用的流量大于5G时,选择套餐一比较合算;
如果每个月使用的流量小于5G时,选择套餐二比较合算.
目前受疫情影响,学生只能在家网络学习.某偏远地区的郝同学因家中没有网络,只能选择用手机流量上课.某电信公司有两种手机流量收费业务.套餐一规定每月月租费10元,每使用1G流量收费2元;套餐二不收月租费,但每使用1G流量收费4元.你认为郝同学选择哪种套餐更合算?
概括总结
方案选择问题解题思路:
(1)根据题意分别写出方案A、B的函数解析式yA、yB;
(2)将方案A、B进行比较:①yA>yB , ②yA<yB , ③yA=yB;解方程或不等式从而分别得到自变量的取值范围;
(3)根据实际情况选择方案.
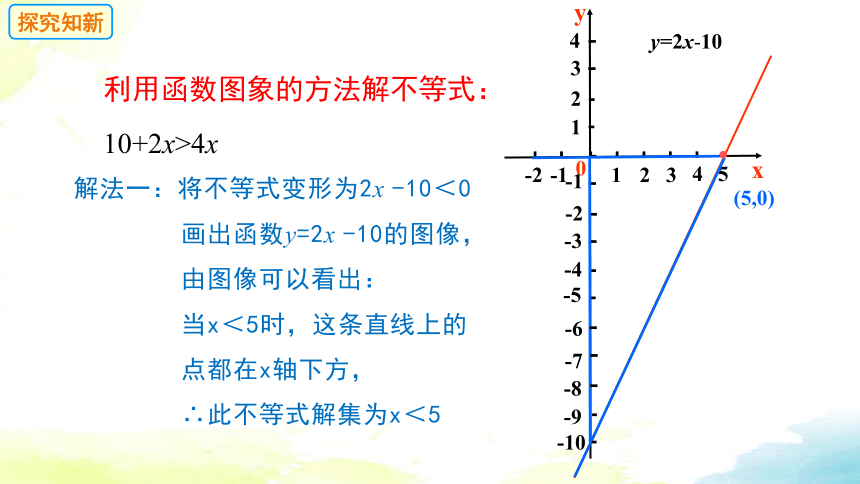
探究知新
利用函数图象的方法解不等式:
10+2x>4x
解法一:将不等式变形为2x -10<0
画出函数y=2x -10的图像,
由图像可以看出:
当x<5时,这条直线上的
点都在x轴下方,
∴此不等式解集为x<5
0
1
2
3
4
5
-2
-1
x
2
-1
3
1
4
-3
-5
-2
-4
y
y=2x-10
(5,0)
-6
-8
-10
-7
-9
探究知新
利用函数图象的方法解不等式:
10+2x>4x
解法二:画出函数y=2x +10与y=4x的图像
由图像可知,交点的横坐标为5.
当x<5时,直线y=2x +10的点都
在直线 y=4x的上方,即10+2x>4x,
∴此不等式解集为x<5
概括总结
k1x+b1>k2x+b2
表示一条直线在另一条上方时,x的取值范围.
y2=k2x+b2
y1=k1x+b1
做一做
直线l1:y1=kx+b与直线l2:y2=x+a在同一平面直角坐标系中的图象如图所示,则关于kx+b>x+a的不等式的解为( )
A. x>3 B. x<3
C. x=3 D. 无法确定
【解析】从图象可以知道两条直线的交点的横坐标为3,通过观察发现 x<3时, kx+b>x+a.故选B.
典型例题
一元一次不等式与一次函数的综合应用
一
例2:某单位计划在新年期间组织员工到某地旅游,参加旅游的人数估计为10至25人,甲、乙两家旅行社的服务质量相同,且报价都是每人200元.经过协商,甲:每位游客七五折优惠;乙:先免去一位游客的旅游费用,其余游客八折优惠.该选择哪一家旅行社呢?
解:设该单位参加这次旅游的人数是x人,选择甲旅行社时,所需的费用为y1元,选择乙旅行社时,所需的费用为y2元,则:
y1 = 200×0.75x, 即y1 = 150x
y2 = 200×0.8(x-1), 即y2= 160x-160
典型例题
一元一次不等式与一次函数的综合应用
一
由y1 = y2,得150x =160x-160,解得x =16
由y1 > y2,得150x>160x-160,解得x<16
由y1 < y2,得150x<160x-160,解得x>16
因为参加旅游的人数为10~25人,所以:
当 x =16 时,y1 = y2 ,甲、乙两家旅行社的收费相同;
当16当10≤x<16时,y1> y2 ,选择乙旅行社费用较少.
概括总结
方案选择问题解题思路:
在本节问题中,一次函数刻画了问题中两个变量之间存在的一种相互依赖关系,而一元一次不等式则描述了问题中这两个变量满足某些特定条件时的状态.
因此,可以从一次函数的角度解决一元一次不等式的问题,也可以利用一元一次不等式解决一次函数的相关问题.
当堂练习
1.如图是一次函数y=kx+b的图象,当y<2时,x的取值范围是( )
A. x<1 B. x>1
C. x<3 D. x>3
C
当堂练习
2.直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐
标系中的图象如图所示,则关于x的不等式k1x+b>k2x
的解为( )
A.x>-1 B.x<-1
C.x<-2 D.x>-2
B
3.如图,直线y=kx+b经过点A(-1,-2)和点B(-2,0),
直线y=2x过点A,则不等式2x<kx+b<0的解集为( )
A.x<-2 B.-2<x<-1
C.-2<x<0 D.-1<x<0
当堂练习
B
当堂练习
4.某校实行学案式教学,需印制若干份数学学案,印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示:
(1)填空:甲种收费的函数关系式是___________.
乙种收费的函数关系式是___________.
(2)该校某年级每次需印制100~450(含100和450)份学案,选择哪种印刷方式较合算?
y1=0.1x+6
y2=0.12x
由y1 = y2,得0.1x+6=0.12x, 解得x =300
由y1 > y2,得0.1x+6>0.12x,解得x<300
由y1 < y2,得0.1x+6<0.12x,解得x>300
因为需印制100~450(含100和450)份学案,所以:
当 x =300 时,y1 = y2 ,甲、乙两种方式一样合算;
当100≤x<300时,y1> y2 ,选择乙种方式合算;
当300<x≤450时,y1> y2 ,选择甲种方式合算.
当堂练习
课堂小结
一元一次不等式与一次函数在决策型应用题中的应用
实际问题
写出两个函数表达式
不等式
解不等式
画出图象
分析图象
解决问题
延伸拓展
四个“一次”在纠缠
四个“一次”是指一元一次方程、二元一次方程(组)、 一元一次不等式与一次函数.它们之间的关系非常密切,既可以运用函数图象解一元一次不等式和一次方程,也可以运用一元一次不等式和一次方程研究函数问题.四者相互渗透,相互作用.
延伸拓展
一次函数与一元一次方程
0
1
2
3
4
5
-2
-1
x
2
-1
3
1
4
-3
-5
-2
-4
y
y=2x-5
例1:作出函数y=2x-5的图象并观察,
当x取何值时,2x-5=0
当x取何值时,2x-5=3
当x取何值时,2x-5=-5
延伸拓展
一次函数与二元一次方程(组)
例2:如图,一次函数y=kx+b与y=x+2的图象相交于点P(m,4),则关于x,y的二元一次方程组 的解是( )
A. B.
C. D.
C
延伸拓展
一次函数与一元一次不等式
如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式
x>kx+b>-2的解集为( )
A. x<2 B. x>-1
C. x<1或x>2 D. -1<x<2
D
思考题
如图,直线y=kx和y=ax+4交于A(1,k),则不等式kx-61<x<
y=kx-6
同学们再见
第二章 一元一次不等式与
一元一次不等式组
2.5 一元一次不等式与一次函数(二)
授课人:翠园初级中学 徐怡旭
1.利用一次函数、一元一次不等式及一元一次方程这
三者之间的关系解决生活中的实际问题.(重点、难点)
2.运用数形结合思想方便快捷解决问题.
学习目标
复习导入
一次函数与一元一次不等式
一
“解不等式ax+b>0(a,b为常数,a≠0)”与
“求自变量x在什么范围内,一次函数y=ax+b的值大于0”
这两个问题之间有什么关系?
这两个问题实际上是同一个问题.
由于任何一元一次不等式都可以转化为ax+b>0或ax+b<0(a、b为常数,a≠0)的形式,所以解一元一次不等式可以看作:当对应的一次函数值大于(或小于)0时,求自变量相应的取值范围。
问题情境
目前受疫情影响,学生只能在家网络学习.某偏远地区的郝同学因家中没有网络,只能选择用手机流量上课.某电信公司有两种手机流量收费业务.套餐一规定每月月租费10元,每使用1G流量收费2元;套餐二不收月租费,但每使用1G流量收费4元.你认为郝同学选择哪种套餐更合算?
一元一次不等式与一次函数的综合应用
一
解:设郝同学每月使用的流量为 x G,套餐一每个月的消费额为y1,套餐二每个月的消费额为y2,根据题意可知
y1=10+2x y2=4x
问题情境
一元一次不等式与一次函数的综合应用
一
当两种套餐消费额一样时,
即y1= y2,得10+2x=4x,
解得x=5;
y1=10+2x y2=4x
当两种套餐消费额不一样时,
①由y1>y2,得10+2x>4x,解得x<5;
此时选择套餐二比较合算.
②由y1
此时选择套餐一比较合算.
目前受疫情影响,学生只能在家网络学习.某偏远地区的郝同学因家中没有网络,只能选择用手机流量上课.某电信公司有两种手机流量收费业务.套餐一规定每月月租费10元,每使用1G流量收费2元;套餐二不收月租费,但每使用1G流量收费4元.你认为郝同学选择哪种套餐更合算?
问题情境
一元一次不等式与一次函数的综合应用
一
所以当郝同学每个月使用的流量等于5G时,选择两种套餐一样合算;
如果每个月使用的流量大于5G时,选择套餐一比较合算;
如果每个月使用的流量小于5G时,选择套餐二比较合算.
目前受疫情影响,学生只能在家网络学习.某偏远地区的郝同学因家中没有网络,只能选择用手机流量上课.某电信公司有两种手机流量收费业务.套餐一规定每月月租费10元,每使用1G流量收费2元;套餐二不收月租费,但每使用1G流量收费4元.你认为郝同学选择哪种套餐更合算?
概括总结
方案选择问题解题思路:
(1)根据题意分别写出方案A、B的函数解析式yA、yB;
(2)将方案A、B进行比较:①yA>yB , ②yA<yB , ③yA=yB;解方程或不等式从而分别得到自变量的取值范围;
(3)根据实际情况选择方案.
探究知新
利用函数图象的方法解不等式:
10+2x>4x
解法一:将不等式变形为2x -10<0
画出函数y=2x -10的图像,
由图像可以看出:
当x<5时,这条直线上的
点都在x轴下方,
∴此不等式解集为x<5
0
1
2
3
4
5
-2
-1
x
2
-1
3
1
4
-3
-5
-2
-4
y
y=2x-10
(5,0)
-6
-8
-10
-7
-9
探究知新
利用函数图象的方法解不等式:
10+2x>4x
解法二:画出函数y=2x +10与y=4x的图像
由图像可知,交点的横坐标为5.
当x<5时,直线y=2x +10的点都
在直线 y=4x的上方,即10+2x>4x,
∴此不等式解集为x<5
概括总结
k1x+b1>k2x+b2
表示一条直线在另一条上方时,x的取值范围.
y2=k2x+b2
y1=k1x+b1
做一做
直线l1:y1=kx+b与直线l2:y2=x+a在同一平面直角坐标系中的图象如图所示,则关于kx+b>x+a的不等式的解为( )
A. x>3 B. x<3
C. x=3 D. 无法确定
【解析】从图象可以知道两条直线的交点的横坐标为3,通过观察发现 x<3时, kx+b>x+a.故选B.
典型例题
一元一次不等式与一次函数的综合应用
一
例2:某单位计划在新年期间组织员工到某地旅游,参加旅游的人数估计为10至25人,甲、乙两家旅行社的服务质量相同,且报价都是每人200元.经过协商,甲:每位游客七五折优惠;乙:先免去一位游客的旅游费用,其余游客八折优惠.该选择哪一家旅行社呢?
解:设该单位参加这次旅游的人数是x人,选择甲旅行社时,所需的费用为y1元,选择乙旅行社时,所需的费用为y2元,则:
y1 = 200×0.75x, 即y1 = 150x
y2 = 200×0.8(x-1), 即y2= 160x-160
典型例题
一元一次不等式与一次函数的综合应用
一
由y1 = y2,得150x =160x-160,解得x =16
由y1 > y2,得150x>160x-160,解得x<16
由y1 < y2,得150x<160x-160,解得x>16
因为参加旅游的人数为10~25人,所以:
当 x =16 时,y1 = y2 ,甲、乙两家旅行社的收费相同;
当16
概括总结
方案选择问题解题思路:
在本节问题中,一次函数刻画了问题中两个变量之间存在的一种相互依赖关系,而一元一次不等式则描述了问题中这两个变量满足某些特定条件时的状态.
因此,可以从一次函数的角度解决一元一次不等式的问题,也可以利用一元一次不等式解决一次函数的相关问题.
当堂练习
1.如图是一次函数y=kx+b的图象,当y<2时,x的取值范围是( )
A. x<1 B. x>1
C. x<3 D. x>3
C
当堂练习
2.直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐
标系中的图象如图所示,则关于x的不等式k1x+b>k2x
的解为( )
A.x>-1 B.x<-1
C.x<-2 D.x>-2
B
3.如图,直线y=kx+b经过点A(-1,-2)和点B(-2,0),
直线y=2x过点A,则不等式2x<kx+b<0的解集为( )
A.x<-2 B.-2<x<-1
C.-2<x<0 D.-1<x<0
当堂练习
B
当堂练习
4.某校实行学案式教学,需印制若干份数学学案,印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示:
(1)填空:甲种收费的函数关系式是___________.
乙种收费的函数关系式是___________.
(2)该校某年级每次需印制100~450(含100和450)份学案,选择哪种印刷方式较合算?
y1=0.1x+6
y2=0.12x
由y1 = y2,得0.1x+6=0.12x, 解得x =300
由y1 > y2,得0.1x+6>0.12x,解得x<300
由y1 < y2,得0.1x+6<0.12x,解得x>300
因为需印制100~450(含100和450)份学案,所以:
当 x =300 时,y1 = y2 ,甲、乙两种方式一样合算;
当100≤x<300时,y1> y2 ,选择乙种方式合算;
当300<x≤450时,y1> y2 ,选择甲种方式合算.
当堂练习
课堂小结
一元一次不等式与一次函数在决策型应用题中的应用
实际问题
写出两个函数表达式
不等式
解不等式
画出图象
分析图象
解决问题
延伸拓展
四个“一次”在纠缠
四个“一次”是指一元一次方程、二元一次方程(组)、 一元一次不等式与一次函数.它们之间的关系非常密切,既可以运用函数图象解一元一次不等式和一次方程,也可以运用一元一次不等式和一次方程研究函数问题.四者相互渗透,相互作用.
延伸拓展
一次函数与一元一次方程
0
1
2
3
4
5
-2
-1
x
2
-1
3
1
4
-3
-5
-2
-4
y
y=2x-5
例1:作出函数y=2x-5的图象并观察,
当x取何值时,2x-5=0
当x取何值时,2x-5=3
当x取何值时,2x-5=-5
延伸拓展
一次函数与二元一次方程(组)
例2:如图,一次函数y=kx+b与y=x+2的图象相交于点P(m,4),则关于x,y的二元一次方程组 的解是( )
A. B.
C. D.
C
延伸拓展
一次函数与一元一次不等式
如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式
x>kx+b>-2的解集为( )
A. x<2 B. x>-1
C. x<1或x>2 D. -1<x<2
D
思考题
如图,直线y=kx和y=ax+4交于A(1,k),则不等式kx-6
y=kx-6
同学们再见
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
