【高考题型分类突破】拓展培优05 圆锥曲线中常用的二级结论 2025年高考数学二轮专题复习 学案(含答案)
文档属性
| 名称 | 【高考题型分类突破】拓展培优05 圆锥曲线中常用的二级结论 2025年高考数学二轮专题复习 学案(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 252.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-14 21:27:08 | ||
图片预览




文档简介
拓展培优(五) 圆锥曲线中常用的二级结论
圆锥曲线是数学高考的重点之一,题目往往思维量大、计算烦琐,如果掌握一些常用的二级结论,便能简化思维过程,提高解题速度和准确度,节约做题时间,从而轻松拿高分.
焦点弦的问题
典例1 已知椭圆C:+=1(a>b>0)的左、右焦点分别为F1,F2,P为椭圆C上一点,且|PF1|=4|PF2|,则椭圆C的离心率的取值范围是( ).
A., B.,
C.,1 D.,1
根据椭圆的定义结合已知条件解出|PF2|=,|PF1|=,再根据焦半径的取值范围及椭圆的离心率e∈(0,1),即可解出离心率的取值范围.
典例2 已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l1,l2,直线l1与C交于A,B两点,直线l2与C交于D,E两点,则|AB|+|DE|的最小值为( ).
A.16 B.14 C.12 D.10
方法总结:
焦点弦是圆锥曲线的“动脉神经”,涉及离心率、直线斜率(或倾斜角)、定比分点(向量)、焦半径和焦点弦长等有关知识,集数学知识、思想方法和解题策略于一体.解决此类问题的关键:(1)熟悉常用结论,包括结论的推导方法(常用结论见下);(2)设直线、联立方程、设而不求及应用韦达定理或点差法.
1.焦半径公式——坐标式
(1)如图1,椭圆+=1(a>b>0)的左、右焦点分别为F1,F2,离心率为e,点P(x0,y0)为椭圆上的任意一点,则椭圆的焦半径|PF1|和|PF2|可按下面的公式计算:
①|PF1|=a+ex0;②|PF2|=a-ex0(记忆:左加右减).
(2)如图2,双曲线-=1(a>0,b>0)的左、右焦点分别为F1,F2,离心率为e,点P(x0,y0)为双曲线上的任意一点,则双曲线的焦半径|PF1|和|PF2|可按下面的公式计算:①|PF1|=|ex0+a|;②|PF2|=|ex0-a|(记忆:左加右减).
2.焦半径公式——角度式
(1)椭圆的焦半径公式
如图,已知直线l过左焦点F1,且与椭圆交于A,B两点,设∠AF1F2=α,则焦半径|AF1|=;|BF1|=;+=;|AB|=|AF1|+|BF1|=.最长焦点弦为长轴,最短焦点弦为通径.
(2)双曲线的焦半径公式
如图,已知直线l过左焦点F1,且与双曲线左支交于A,B两点,设∠AF1F2=α,则焦半径|AF1|=;|BF1|=;+=;|AB|=|AF1|+|BF1|=.
(3)抛物线y2=2px(p>0)的焦半径公式
|AF|=,|BF|=(F为抛物线的焦点,AB为焦点弦,α为直线AB的倾斜角,且点A在x轴上方,点B在x轴下方).
3.焦点弦分比定值定理
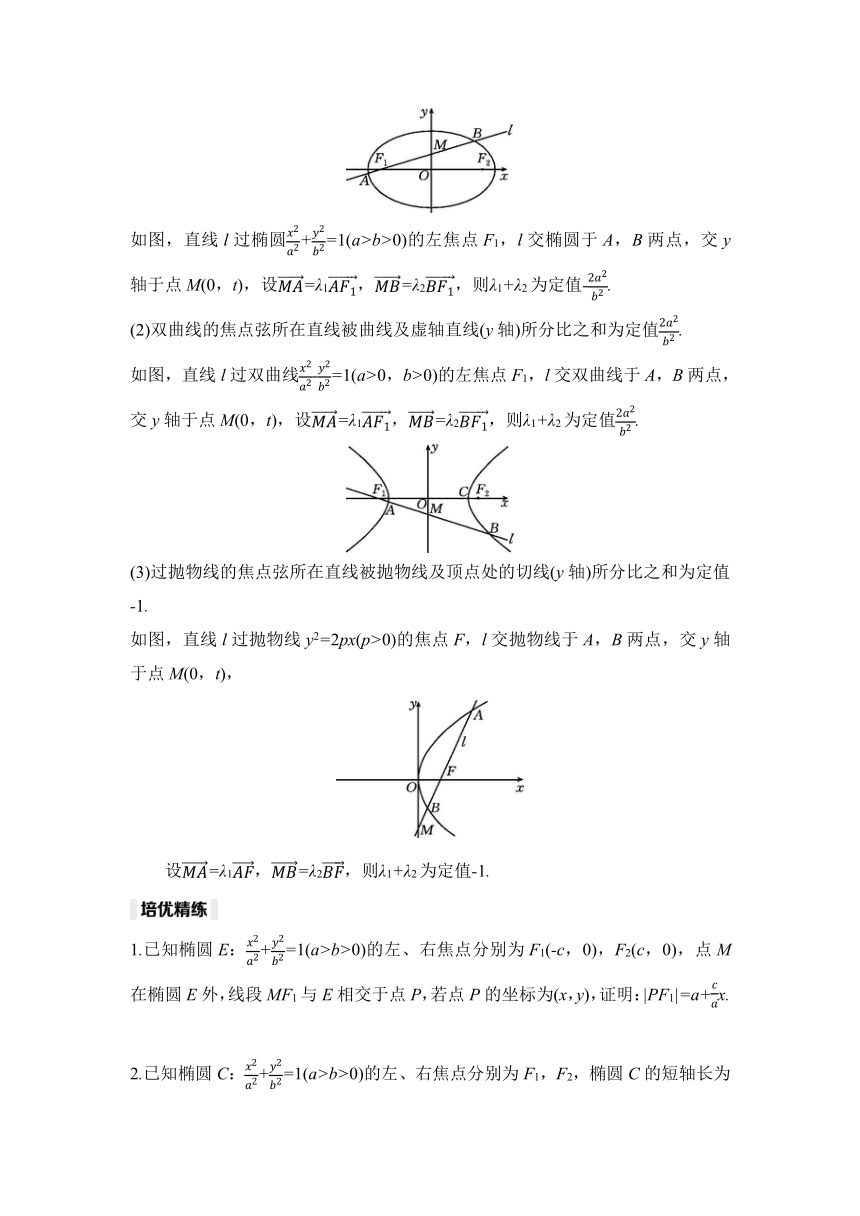
(1)椭圆的焦点弦所在直线被椭圆及短轴所在直线(y轴)所分比之和为定值-.
如图,直线l过椭圆+=1(a>b>0)的左焦点F1,l交椭圆于A,B两点,交y轴于点M(0,t),设=λ1,=λ2,则λ1+λ2为定值-.
(2)双曲线的焦点弦所在直线被曲线及虚轴直线(y轴)所分比之和为定值.
如图,直线l过双曲线-=1(a>0,b>0)的左焦点F1,l交双曲线于A,B两点,交y轴于点M(0,t),设=λ1,=λ2,则λ1+λ2为定值.
(3)过抛物线的焦点弦所在直线被抛物线及顶点处的切线(y轴)所分比之和为定值-1.
如图,直线l过抛物线y2=2px(p>0)的焦点F,l交抛物线于A,B两点,交y轴于点M(0,t),
设=λ1,=λ2,则λ1+λ2为定值-1.
1.已知椭圆E:+=1(a>b>0)的左、右焦点分别为F1(-c,0),F2(c,0),点M在椭圆E外,线段MF1与E相交于点P,若点P的坐标为(x,y),证明:|PF1|=a+x.
2.已知椭圆C:+=1(a>b>0)的左、右焦点分别为F1,F2,椭圆C的短轴长为2,离心率为.点P(x0,y0)为椭圆C上的一个动点,直线PF1与椭圆C的另一个交点为A,直线PF2与椭圆C的另一个交点为B,设=λ1,=λ2.
(1)求椭圆C的方程.
(2)证明:λ1+λ2为定值.
等角的性质
典例3 设椭圆C:+=1的右焦点为F,过F的直线l与C交于A,B两点,点M的坐标为(3,0).
(1)当l与x轴垂直时,求直线AM的方程.
(2)设O为坐标原点,证明:∠OMA=∠OMB.
方法总结:
圆锥曲线中证明角度相等常用的定理有角平分线定理、余弦定理、斜率等.解决方法如下:
1.将角度问题转化为斜率问题.设直线方程为y=kx+m时要讨论斜率是否存在;设直线方程为ty+m=x时要注意该方程无法表示倾斜角为0°的直线.
2.利用等角性质定理:
(1)椭圆等角定理:过椭圆+=1(a>b>0)长轴上任意一点N(t,0)(t≠0)的一条弦的端点与对应点G,0的连线所成的角被焦点所在直线平分.
(2)双曲线等角定理:过双曲线-=1(a>0,b>0)实轴上任意一点N(t,0)(t≠0)的一条弦的端点与对应点G,0的连线所成的角被焦点所在直线平分.
(3)抛物线等角定理:过抛物线y2=2px(p>0)对称轴上任意一点N(a,0)(a>0)的一条弦的端点与对应点G(-a,0)的连线所成的角被对称轴平分.
如果题目符合等角性质定理的条件,那么对于客观题可直接运用,对于主观题,可结合定理正向、逆向思维,加快解题进程.
已知点A是圆C:(x-1)2+y2=16上的任意一点,点F(-1,0),线段AF的垂直平分线交AC于点P.
(1)求动点P的轨迹E的方程.
(2)若过点G(3,0)且斜率不为0的直线l交(1)中轨迹E于M,N两点,O为坐标原点,点B(2,0).问:x轴上是否存在定点T,使得∠MTO=∠NTB恒成立.若存在,请求出点T的坐标;若不存在,请说明理由.
切线、切点弦方程
典例4 (1)已知抛物线C:x2=4y的焦点为F,A是抛物线C上的一点,且点A在第一象限,若|AF|=4,则抛物线C在点A处的切线方程为( ).
A.x-y-3=0 B.2x-y-1=0
C.x-y-1=0 D.x-y-2=0
(2)已知抛物线C:y2=2px(p>0)上的一点处的切线方程为y-x-1=0,A,B为C上两动点,且|AB|=6,则AB的中点M到y轴的距离的取值范围为( ).
A.[2,+∞) B.,+∞
C.[3,+∞) D.,+∞
(3)已知P(x0,y0)(x0≠0)是抛物线C1:y2=-4x上一点,过点P作抛物线C2:y2=4x的两条切线PM,PN,切点分别为M,N,H为线段MN的中点,F为C2的焦点,则( ).
A.若x0=-1,则直线MN经过点F
B.直线PH⊥y轴
C.点H的轨迹方程为y2=x
D.∠PFM=∠PFN
(1)设A(x1,y1),先根据抛物线的定义解出A点坐标;接下来的思路有两条:一是运用抛物线上的点的切线方程结论直接求解;二是根据导函数的几何意义求出切线斜率,由点斜式写出方程.
(2)思路一:根据抛物线上的点的切线方程结论,求得p,接着设出A(x1,y1),B(x2,y2),表示出点M到y轴的距离d,然后利用抛物线的定义,将其转化为两条焦半径的和,结合图形易得d≥2,从而得解.思路二:通过求导数,设切点,求出p=2.后同思路一.
(3)利用抛物线上的点的切线方程结论,先表示出切线方程,联立方程,得直线MN的方程为y0y=2(x0+x),解得y=,从而得P,,可判定A,B;再由点H,,可得轨迹方程,判定C;由向量的坐标运算得cos∠PFM==,cos∠PFN=,判定D.
方法总结:
1.椭圆与切线
(1)点M(x0,y0)在椭圆+=1(a>b>0)上,过点M作椭圆的切线,切线方程为+=1.
(2)点M(x0,y0)在椭圆+=1(a>b>0)外,过点M作椭圆的两条切线,切点分别为A,B,则切点弦AB的直线方程为+=1.
(3)点M(x0,y0)在椭圆+=1(a>b>0)内,过点M作椭圆的弦AB(不过椭圆中心),分别过A,B作椭圆的切线,则两条切线的交点P的轨迹方程为+=1.
2.双曲线与切线
(1)点M(x0,y0)在双曲线-=1(a>0,b>0)上,过点M作双曲线的切线,切线方程为-=1.
(2)点M(x0,y0)在双曲线-=1(a>0,b>0)外,过点M作双曲线的两条切线,切点分别为A,B,则切点弦AB的直线方程为-=1.
(3)点M(x0,y0)在双曲线-=1(a>0,b>0)内,过点M作双曲线的弦AB(不过双曲线中心),分别过A,B作双曲线的切线,则两条切线的交点P的轨迹方程为-=1.
3.抛物线与切线
(1)点M(x0,y0)在抛物线y2=2px(p>0)上,过点M作抛物线的切线,切线方程为y0y=p(x+x0).
(2)点M(x0,y0)在抛物线y2=2px(p>0)外,过点M作抛物线的两条切线,切点分别为A,B,则切点弦AB的直线方程为y0y=p(x+x0).
(3)点M(x0,y0)在抛物线y2=2px(p>0)内,过点M作抛物线的弦AB,分别过A,B作抛物线的切线,则两条切线的交点P的轨迹方程为y0y=p(x+x0).
1.与抛物线x2=2y和圆x2+(y+1)2=1都相切的直线的条数为( ).
A.0 B.1 C.2 D.3
2.已知直线y=x+m与抛物线C:y2=8x相切于点P,过P作两条斜率互为相反数的直线,这两条直线与C的另一个交点分别为A,B,直线y=2x-4与C交于M,N两点,则( ).
A.m=4
B.线段AB中点的纵坐标为-4
C.直线AB的斜率为-1
D.直线PM,PN的斜率之积为4
3.已知椭圆C:+=1(a>b>0)的离心率为,短轴长为2.
(1)求椭圆C的方程;
(2)设O为坐标原点,过点P-1,-分别作直线l1,l2,直线l1与椭圆相切于第三象限内的点G,直线l2交椭圆C于M,N两点,若|PG|2=|PM|·|PN|,判断直线l2与直线OG的位置关系,并说明理由.
参考答案
拓展培优(五) 圆锥曲线中常用的二级结论
考向1 焦点弦的问题
典例1 D
【解析】(法一)因为|PF1|=4|PF2|,|PF1|+|PF2|=2a,所以4|PF2|+|PF2|=2a,故|PF2|=,|PF1|=.
因为|PF1|∈[a-c,a+c],所以a-c≤≤a+c,
即1-e≤≤1+e,解得e≥,又因为椭圆的离心率e∈(0,1),所以e∈,1.
(法二)设点P的坐标为(x0,y0),因为|PF1|=4|PF2|,所以a+ex0=4(a-ex0),整理得e=,因为0典例2 A
【解析】设l1的倾斜角为θ,不妨设θ∈,那么|AB|==,因为l1⊥l2,所以l2的倾斜角为θ++或θ-,|DE|==,求|AB|+|DE|的最小值,即求4+在0,上的最小值,因为4+=,所以令f(θ)=.
当sin θcos θ取得最大值,即θ=时,f(θ)取得最小值,最小值为f==16.
故|AB|+|DE|的最小值为16.
培优精练
1.解析 由题意可知|PF1|=,|PF2|=,
则-=4cx,
因为|PF1|+|PF2|=2a,即|PF2|=2a-|PF1|,
所以-(2a-|PF1|)2=4cx,整理得4a|PF1|=4a2+4cx,
所以|PF1|=a+x.
2.解析 (1)由题意知2b=2,得b=,又===,解得a=,
所以椭圆C的方程为+=1.
(2)如图,由(1)知F1(-1,0),F2(1,0),设A(x1,y1),B(x2,y2),
则=(-1-x0,-y0),=(x1+1,y1),=(1-x0,-y0),=(x2-1,y2),
由=λ1,得所以
又点A(x1,y1)在椭圆上,所以+=1,即+=.
又+=1,所以+1-=,即(1+x0+λ1)2+3--3=0.
将其展开,得到-2+2(1+x0)λ1+(1+x0)2+3-=0,即-2+2(1+x0)λ1+2x0+4=0.
从而-(1+x0)λ1-x0-2=0,即(λ1+1)(λ1-2-x0)=0,
易知λ1>0,所以λ1-2-x0=0,得λ1=2+x0,
同理,由=λ2,得所以
又点B(x2,y2)在椭圆上,所以+=1,即+=.
又+=1,所以+1-=,即(1-x0+λ2)2+3--3=0.
将其展开,得到-2+2(1-x0)λ2+(1-x0)2+3-=0,即-2+2(1-x0)λ2-2x0+4=0.
从而-(1-x0)λ2+x0-2=0,即(λ2+1)(λ2-2+x0)=0,
易知λ2>0,所以λ2-2+x0=0,得λ2=2-x0,所以λ1+λ2=4,即λ1+λ2为定值.
考向2 等角的性质
典例3
【解析】(1)由题意得a2=3,b2=2,c2=a2-b2=1,所以c=1,则F(1,0).
当l与x轴垂直时,直线l的方程为x=1.
联立直线与椭圆C的方程,得解得或
所以点A的坐标为1,或1,-.
当点A的坐标为1,时,可得kAM==-,所以直线AM的方程为y=-(x-3),整理可得x+y-3=0;
当点A的坐标为1,-时,可得kAM==,所以直线AM的方程为y=(x-3),整理可得x-y-3=0.
综上所述,直线AM的方程为x+y-3=0或x-y-3=0.
(2)
(法一)当直线l与x轴重合时,∠OMA=∠OMB=0°,结论成立.
当直线l与x轴不重合时,可设直线l的方程为x=my+1.
设A(x1,y1),B(x2,y2),
由可得(2m2+3)y2+4my-4=0.
显然Δ>0,由韦达定理可知且x1=my1+1,x2=my2+1.
因为my1y2-(y1+y2)=---=0,
所以my1y2=y1+y2.
所以kMA+kMB=+====0,
所以直线MA,MB的倾斜角互补,
所以∠OMA=∠OMB.
综上所述,∠OMA=∠OMB.
(法二)当l与x轴重合时,∠OMA=∠OMB=0°,
当l与x轴垂直时,OM为AB的垂直平分线,∴∠OMA=∠OMB,
当l与x轴不重合也不垂直时,设l的方程为y=k(x-1),k≠0,
联立y=k(x-1)和+=1,得(3k2+2)x2-6k2x+3k2-6=0.
设A(x1,y1),B(x2,y2),则x1<,x2<,且x1+x2=,x1x2=,y1=k(x1-1),y2=k(x2-1),
所以kMA+kMB=+=,
而2kx1x2-4k(x1+x2)+6k=(3k2-6-12k2+9k2+6)=0,进而kMA+kMB=0,
故MA,MB的倾斜角互补,所以∠OMA=∠OMB.
综上所述,∠OMA=∠OMB.
培优精练
【解析】(1)由圆C:(x-1)2+y2=16,可得圆心坐标为C(1,0),半径r=4,
如图所示,线段AF的垂直平分线交AC于点P,
所以|PF|+|PC|=|PA|+|PC|=4>|FC|=2,
根据椭圆的定义,可知点P的轨迹是以F,C为焦点的椭圆,且2a=4,2c=2,
可得a=2,c=1,则b==,
所以动点P的轨迹方程为+=1.
(2)由题意知直线l的斜率不为0.
当直线l与x轴垂直时,无交点M,N,舍去.
当直线l与x轴不重合也不垂直时,设直线l的方程为y=k(x-3),且k≠0,
由整理得(3+4k2)x2-24k2x+36k2-12=0,由Δ>0,解得-设M(x1,y1),N(x2,y2),则x1+x2=,x1x2=,
根据椭圆的对称性,不妨令点M,N在x轴上方,且x2>x1,
假设存在T(t,0),使得∠MTO=∠NTB恒成立,即tan∠MTO=tan∠NTB恒成立,显然x1可得kMT=-kNT,即kMT+kNT=0恒成立,即+=0恒成立.
又由+=,
得t(y1+y2)-x1y2-x2y1=0,
所以t======,
所以存在点T,0,使得∠MTO=∠NTB恒成立.
考向3 切线、切点弦方程
典例4 (1)A (2)A (3)ABD
【解析】(1)(法一)设A(x1,y1),由x2=4y,得p=2,所以抛物线的准线方程为y=-1.
由抛物线的定义可得|AF|=y1+1=4,得y1=3,代入x2=4y,得x1=±2,
又点A在第一象限,所以x1=2,所以点A的坐标为(2,3),
所以抛物线C:x2=4y在点A处的切线方程为2x=2(y+3),即x-y-3=0.
(法二)同法一得A(2,3),由x2=4y,得y=x2,所以y'=x,所以抛物线C在点A处的切线方程的斜率为×2=,
所以抛物线C在点A处的切线方程为y-3=(x-2),即x-y-3=0.
(2)(法一)因为抛物线C:y2=2px(p>0)上的一点D(x0,y0)处的切线方程为y0y=p(x+x0),即y0y=px+,整理可得y-x-=0,又由题意知该切线方程为y-x-1=0,所以可得y0=p=2,故C的方程为y2=4x.
如图,设点A(x1,y1),B(x2,y2),则M,,点M到y轴的距离d==-1=-1≥-1=2,
当且仅当线段AB经过点F时,等号成立.故AB的中点M到y轴的距离的取值范围为[2,+∞).
(法二)依题意知,切线的斜率为1,故切点必在第一象限,设切点为(x0,y0)(x0>0,y0>0),即,y0,由y=求导可得y'=,
则=1,即=1,化简得y0=p,故切点为,p,代入y-x-1=0中,解得p=2,故C的方程为y2=4x.
以下同法一,可得AB的中点M到y轴的距离的取值范围为[2,+∞).
(3)设M(x1,y1),N(x2,y2),
则过点M的切线方程为y1y=2(x1+x),过点N的切线方程为y2y=2(x2+x),
由题意知这两条切线交于点P(x0,y0),则
从而直线MN的方程为y0y=2(x0+x).
若x0=-1,则直线MN经过点F(1,0),A正确.
因为点M,N在C2上,所以
所以由
解得y=,
即y0=,从而x0=,即P,.
因为H为线段MN的中点,所以H,,
所以PH⊥y轴,B正确.
因为点H,,==-x0=,=y0,
所以点H的轨迹方程为y2=x(x≠0),C错误.
因为=(x0-1,y0),=(x1-1,y1),=(x2-1,y2),
所以·=(x0-1,y0)·(x1-1,y1)=x0x1-x1-x0+1+y0y1=x0x1-x1-x0+1+2(x0+x1)=(x0+1)(x1+1).
又|MF|=x1+1,所以cos ∠PFM==,
同理可得cos ∠PFN=,从而∠PFM=∠PFN,D正确.故选ABD.
培优精练
1.D
【解析】设直线与抛物线x2=2y相切的切点坐标为t,t2,由y=x2求导得y'=x,
因此抛物线x2=2y在点t,t2处的切线方程为y-t2=t(x-t),即tx-y-t2=0,
依题意,此切线与圆x2+(y+1)2=1相切,于是=1,解得t=0或t=±2,所以所求切线的条数为3.故选D.
2.BCD
【解析】对于A,由得x2+(2m-8)x+m2=0,
由Δ=(2m-8)2-4m2=0,解得m=2,故A错误;
对于B,由m=2,得x2-4x+4=0,故x=2,y=2+2=4,故P点坐标为(2,4),
设lPA:y=k(x-2)+4,则lPB:y=-k(x-2)+4,k≠0,
联立lPA与抛物线的方程,得消去x可得ky2-8y+32-16k=0,
Δ=64-4k(32-16k)=64(k-1)2>0,即k≠1,则有yA+4=,即yA=-4,
同理可得yB=--4,故==-4,故B正确;
对于C,kAB=====-1,故C正确;
对于D,由题意可得kPM====,
同理可得kPN=,则kPM·kPN=·=,
联立lMN与抛物线的方程,得消去x可得y2-4y-16=0,
故yM+yN=4,yMyN=-16,
即有kPM·kPN===4,故D正确.故选BCD.
3.解析 (1)由题意得解得
所以椭圆C的方程为+=1.
(2)直线l2与直线OG平行.证明如下:
显然直线l1的斜率存在,设直线l1的方程为y+=m(x+1).
由得(4m2+1)x2+(8m2-12m)x+4m2-12m+1=0.
因为直线l1与椭圆相切,
所以Δ=(8m2-12m)2-4(4m2+1)(4m2-12m+1)=4(28m2+12m-1)=0,
解得m=-或m=.
因为直线l1与椭圆相切于第三象限内的点G,所以m=-,所以2x2+8x+8=0,xG=-2,
所以yG=-(xG+1)-=-1,
所以点G的坐标为(-2,-1),直线OG的斜率为,|PG|2=.
当直线l2的斜率不存在时,|PM||PN|=,所以|PG|2≠|PM|·|PN|.
当直线l2的斜率存在时,设直线l2的方程为y+=k(x+1),M(x1,y1),N(x2,y2).
由得(4k2+1)x2+(8k2-12k)x+4k2-12k+1=0,
直线l2交椭圆C于M,N两点,Δ=4(28k2+12k-1)>0,
所以k<-或k>,所以x1+x2=,x1x2=.
|PM|==|x1+1|,同理得|PN|=|x2+1|,
所以|PM|·|PN|=(1+k2)|x1+1||x2+1|=(1+k2)|x1x2+(x1+x2)+1|=(1+k2).
所以(1+k2)=,解得k=或k=-,
又k<-或k>,所以k=,所以直线l2与直线OG平行.
圆锥曲线是数学高考的重点之一,题目往往思维量大、计算烦琐,如果掌握一些常用的二级结论,便能简化思维过程,提高解题速度和准确度,节约做题时间,从而轻松拿高分.
焦点弦的问题
典例1 已知椭圆C:+=1(a>b>0)的左、右焦点分别为F1,F2,P为椭圆C上一点,且|PF1|=4|PF2|,则椭圆C的离心率的取值范围是( ).
A., B.,
C.,1 D.,1
根据椭圆的定义结合已知条件解出|PF2|=,|PF1|=,再根据焦半径的取值范围及椭圆的离心率e∈(0,1),即可解出离心率的取值范围.
典例2 已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l1,l2,直线l1与C交于A,B两点,直线l2与C交于D,E两点,则|AB|+|DE|的最小值为( ).
A.16 B.14 C.12 D.10
方法总结:
焦点弦是圆锥曲线的“动脉神经”,涉及离心率、直线斜率(或倾斜角)、定比分点(向量)、焦半径和焦点弦长等有关知识,集数学知识、思想方法和解题策略于一体.解决此类问题的关键:(1)熟悉常用结论,包括结论的推导方法(常用结论见下);(2)设直线、联立方程、设而不求及应用韦达定理或点差法.
1.焦半径公式——坐标式
(1)如图1,椭圆+=1(a>b>0)的左、右焦点分别为F1,F2,离心率为e,点P(x0,y0)为椭圆上的任意一点,则椭圆的焦半径|PF1|和|PF2|可按下面的公式计算:
①|PF1|=a+ex0;②|PF2|=a-ex0(记忆:左加右减).
(2)如图2,双曲线-=1(a>0,b>0)的左、右焦点分别为F1,F2,离心率为e,点P(x0,y0)为双曲线上的任意一点,则双曲线的焦半径|PF1|和|PF2|可按下面的公式计算:①|PF1|=|ex0+a|;②|PF2|=|ex0-a|(记忆:左加右减).
2.焦半径公式——角度式
(1)椭圆的焦半径公式
如图,已知直线l过左焦点F1,且与椭圆交于A,B两点,设∠AF1F2=α,则焦半径|AF1|=;|BF1|=;+=;|AB|=|AF1|+|BF1|=.最长焦点弦为长轴,最短焦点弦为通径.
(2)双曲线的焦半径公式
如图,已知直线l过左焦点F1,且与双曲线左支交于A,B两点,设∠AF1F2=α,则焦半径|AF1|=;|BF1|=;+=;|AB|=|AF1|+|BF1|=.
(3)抛物线y2=2px(p>0)的焦半径公式
|AF|=,|BF|=(F为抛物线的焦点,AB为焦点弦,α为直线AB的倾斜角,且点A在x轴上方,点B在x轴下方).
3.焦点弦分比定值定理
(1)椭圆的焦点弦所在直线被椭圆及短轴所在直线(y轴)所分比之和为定值-.
如图,直线l过椭圆+=1(a>b>0)的左焦点F1,l交椭圆于A,B两点,交y轴于点M(0,t),设=λ1,=λ2,则λ1+λ2为定值-.
(2)双曲线的焦点弦所在直线被曲线及虚轴直线(y轴)所分比之和为定值.
如图,直线l过双曲线-=1(a>0,b>0)的左焦点F1,l交双曲线于A,B两点,交y轴于点M(0,t),设=λ1,=λ2,则λ1+λ2为定值.
(3)过抛物线的焦点弦所在直线被抛物线及顶点处的切线(y轴)所分比之和为定值-1.
如图,直线l过抛物线y2=2px(p>0)的焦点F,l交抛物线于A,B两点,交y轴于点M(0,t),
设=λ1,=λ2,则λ1+λ2为定值-1.
1.已知椭圆E:+=1(a>b>0)的左、右焦点分别为F1(-c,0),F2(c,0),点M在椭圆E外,线段MF1与E相交于点P,若点P的坐标为(x,y),证明:|PF1|=a+x.
2.已知椭圆C:+=1(a>b>0)的左、右焦点分别为F1,F2,椭圆C的短轴长为2,离心率为.点P(x0,y0)为椭圆C上的一个动点,直线PF1与椭圆C的另一个交点为A,直线PF2与椭圆C的另一个交点为B,设=λ1,=λ2.
(1)求椭圆C的方程.
(2)证明:λ1+λ2为定值.
等角的性质
典例3 设椭圆C:+=1的右焦点为F,过F的直线l与C交于A,B两点,点M的坐标为(3,0).
(1)当l与x轴垂直时,求直线AM的方程.
(2)设O为坐标原点,证明:∠OMA=∠OMB.
方法总结:
圆锥曲线中证明角度相等常用的定理有角平分线定理、余弦定理、斜率等.解决方法如下:
1.将角度问题转化为斜率问题.设直线方程为y=kx+m时要讨论斜率是否存在;设直线方程为ty+m=x时要注意该方程无法表示倾斜角为0°的直线.
2.利用等角性质定理:
(1)椭圆等角定理:过椭圆+=1(a>b>0)长轴上任意一点N(t,0)(t≠0)的一条弦的端点与对应点G,0的连线所成的角被焦点所在直线平分.
(2)双曲线等角定理:过双曲线-=1(a>0,b>0)实轴上任意一点N(t,0)(t≠0)的一条弦的端点与对应点G,0的连线所成的角被焦点所在直线平分.
(3)抛物线等角定理:过抛物线y2=2px(p>0)对称轴上任意一点N(a,0)(a>0)的一条弦的端点与对应点G(-a,0)的连线所成的角被对称轴平分.
如果题目符合等角性质定理的条件,那么对于客观题可直接运用,对于主观题,可结合定理正向、逆向思维,加快解题进程.
已知点A是圆C:(x-1)2+y2=16上的任意一点,点F(-1,0),线段AF的垂直平分线交AC于点P.
(1)求动点P的轨迹E的方程.
(2)若过点G(3,0)且斜率不为0的直线l交(1)中轨迹E于M,N两点,O为坐标原点,点B(2,0).问:x轴上是否存在定点T,使得∠MTO=∠NTB恒成立.若存在,请求出点T的坐标;若不存在,请说明理由.
切线、切点弦方程
典例4 (1)已知抛物线C:x2=4y的焦点为F,A是抛物线C上的一点,且点A在第一象限,若|AF|=4,则抛物线C在点A处的切线方程为( ).
A.x-y-3=0 B.2x-y-1=0
C.x-y-1=0 D.x-y-2=0
(2)已知抛物线C:y2=2px(p>0)上的一点处的切线方程为y-x-1=0,A,B为C上两动点,且|AB|=6,则AB的中点M到y轴的距离的取值范围为( ).
A.[2,+∞) B.,+∞
C.[3,+∞) D.,+∞
(3)已知P(x0,y0)(x0≠0)是抛物线C1:y2=-4x上一点,过点P作抛物线C2:y2=4x的两条切线PM,PN,切点分别为M,N,H为线段MN的中点,F为C2的焦点,则( ).
A.若x0=-1,则直线MN经过点F
B.直线PH⊥y轴
C.点H的轨迹方程为y2=x
D.∠PFM=∠PFN
(1)设A(x1,y1),先根据抛物线的定义解出A点坐标;接下来的思路有两条:一是运用抛物线上的点的切线方程结论直接求解;二是根据导函数的几何意义求出切线斜率,由点斜式写出方程.
(2)思路一:根据抛物线上的点的切线方程结论,求得p,接着设出A(x1,y1),B(x2,y2),表示出点M到y轴的距离d,然后利用抛物线的定义,将其转化为两条焦半径的和,结合图形易得d≥2,从而得解.思路二:通过求导数,设切点,求出p=2.后同思路一.
(3)利用抛物线上的点的切线方程结论,先表示出切线方程,联立方程,得直线MN的方程为y0y=2(x0+x),解得y=,从而得P,,可判定A,B;再由点H,,可得轨迹方程,判定C;由向量的坐标运算得cos∠PFM==,cos∠PFN=,判定D.
方法总结:
1.椭圆与切线
(1)点M(x0,y0)在椭圆+=1(a>b>0)上,过点M作椭圆的切线,切线方程为+=1.
(2)点M(x0,y0)在椭圆+=1(a>b>0)外,过点M作椭圆的两条切线,切点分别为A,B,则切点弦AB的直线方程为+=1.
(3)点M(x0,y0)在椭圆+=1(a>b>0)内,过点M作椭圆的弦AB(不过椭圆中心),分别过A,B作椭圆的切线,则两条切线的交点P的轨迹方程为+=1.
2.双曲线与切线
(1)点M(x0,y0)在双曲线-=1(a>0,b>0)上,过点M作双曲线的切线,切线方程为-=1.
(2)点M(x0,y0)在双曲线-=1(a>0,b>0)外,过点M作双曲线的两条切线,切点分别为A,B,则切点弦AB的直线方程为-=1.
(3)点M(x0,y0)在双曲线-=1(a>0,b>0)内,过点M作双曲线的弦AB(不过双曲线中心),分别过A,B作双曲线的切线,则两条切线的交点P的轨迹方程为-=1.
3.抛物线与切线
(1)点M(x0,y0)在抛物线y2=2px(p>0)上,过点M作抛物线的切线,切线方程为y0y=p(x+x0).
(2)点M(x0,y0)在抛物线y2=2px(p>0)外,过点M作抛物线的两条切线,切点分别为A,B,则切点弦AB的直线方程为y0y=p(x+x0).
(3)点M(x0,y0)在抛物线y2=2px(p>0)内,过点M作抛物线的弦AB,分别过A,B作抛物线的切线,则两条切线的交点P的轨迹方程为y0y=p(x+x0).
1.与抛物线x2=2y和圆x2+(y+1)2=1都相切的直线的条数为( ).
A.0 B.1 C.2 D.3
2.已知直线y=x+m与抛物线C:y2=8x相切于点P,过P作两条斜率互为相反数的直线,这两条直线与C的另一个交点分别为A,B,直线y=2x-4与C交于M,N两点,则( ).
A.m=4
B.线段AB中点的纵坐标为-4
C.直线AB的斜率为-1
D.直线PM,PN的斜率之积为4
3.已知椭圆C:+=1(a>b>0)的离心率为,短轴长为2.
(1)求椭圆C的方程;
(2)设O为坐标原点,过点P-1,-分别作直线l1,l2,直线l1与椭圆相切于第三象限内的点G,直线l2交椭圆C于M,N两点,若|PG|2=|PM|·|PN|,判断直线l2与直线OG的位置关系,并说明理由.
参考答案
拓展培优(五) 圆锥曲线中常用的二级结论
考向1 焦点弦的问题
典例1 D
【解析】(法一)因为|PF1|=4|PF2|,|PF1|+|PF2|=2a,所以4|PF2|+|PF2|=2a,故|PF2|=,|PF1|=.
因为|PF1|∈[a-c,a+c],所以a-c≤≤a+c,
即1-e≤≤1+e,解得e≥,又因为椭圆的离心率e∈(0,1),所以e∈,1.
(法二)设点P的坐标为(x0,y0),因为|PF1|=4|PF2|,所以a+ex0=4(a-ex0),整理得e=,因为0
【解析】设l1的倾斜角为θ,不妨设θ∈,那么|AB|==,因为l1⊥l2,所以l2的倾斜角为θ++或θ-,|DE|==,求|AB|+|DE|的最小值,即求4+在0,上的最小值,因为4+=,所以令f(θ)=.
当sin θcos θ取得最大值,即θ=时,f(θ)取得最小值,最小值为f==16.
故|AB|+|DE|的最小值为16.
培优精练
1.解析 由题意可知|PF1|=,|PF2|=,
则-=4cx,
因为|PF1|+|PF2|=2a,即|PF2|=2a-|PF1|,
所以-(2a-|PF1|)2=4cx,整理得4a|PF1|=4a2+4cx,
所以|PF1|=a+x.
2.解析 (1)由题意知2b=2,得b=,又===,解得a=,
所以椭圆C的方程为+=1.
(2)如图,由(1)知F1(-1,0),F2(1,0),设A(x1,y1),B(x2,y2),
则=(-1-x0,-y0),=(x1+1,y1),=(1-x0,-y0),=(x2-1,y2),
由=λ1,得所以
又点A(x1,y1)在椭圆上,所以+=1,即+=.
又+=1,所以+1-=,即(1+x0+λ1)2+3--3=0.
将其展开,得到-2+2(1+x0)λ1+(1+x0)2+3-=0,即-2+2(1+x0)λ1+2x0+4=0.
从而-(1+x0)λ1-x0-2=0,即(λ1+1)(λ1-2-x0)=0,
易知λ1>0,所以λ1-2-x0=0,得λ1=2+x0,
同理,由=λ2,得所以
又点B(x2,y2)在椭圆上,所以+=1,即+=.
又+=1,所以+1-=,即(1-x0+λ2)2+3--3=0.
将其展开,得到-2+2(1-x0)λ2+(1-x0)2+3-=0,即-2+2(1-x0)λ2-2x0+4=0.
从而-(1-x0)λ2+x0-2=0,即(λ2+1)(λ2-2+x0)=0,
易知λ2>0,所以λ2-2+x0=0,得λ2=2-x0,所以λ1+λ2=4,即λ1+λ2为定值.
考向2 等角的性质
典例3
【解析】(1)由题意得a2=3,b2=2,c2=a2-b2=1,所以c=1,则F(1,0).
当l与x轴垂直时,直线l的方程为x=1.
联立直线与椭圆C的方程,得解得或
所以点A的坐标为1,或1,-.
当点A的坐标为1,时,可得kAM==-,所以直线AM的方程为y=-(x-3),整理可得x+y-3=0;
当点A的坐标为1,-时,可得kAM==,所以直线AM的方程为y=(x-3),整理可得x-y-3=0.
综上所述,直线AM的方程为x+y-3=0或x-y-3=0.
(2)
(法一)当直线l与x轴重合时,∠OMA=∠OMB=0°,结论成立.
当直线l与x轴不重合时,可设直线l的方程为x=my+1.
设A(x1,y1),B(x2,y2),
由可得(2m2+3)y2+4my-4=0.
显然Δ>0,由韦达定理可知且x1=my1+1,x2=my2+1.
因为my1y2-(y1+y2)=---=0,
所以my1y2=y1+y2.
所以kMA+kMB=+====0,
所以直线MA,MB的倾斜角互补,
所以∠OMA=∠OMB.
综上所述,∠OMA=∠OMB.
(法二)当l与x轴重合时,∠OMA=∠OMB=0°,
当l与x轴垂直时,OM为AB的垂直平分线,∴∠OMA=∠OMB,
当l与x轴不重合也不垂直时,设l的方程为y=k(x-1),k≠0,
联立y=k(x-1)和+=1,得(3k2+2)x2-6k2x+3k2-6=0.
设A(x1,y1),B(x2,y2),则x1<,x2<,且x1+x2=,x1x2=,y1=k(x1-1),y2=k(x2-1),
所以kMA+kMB=+=,
而2kx1x2-4k(x1+x2)+6k=(3k2-6-12k2+9k2+6)=0,进而kMA+kMB=0,
故MA,MB的倾斜角互补,所以∠OMA=∠OMB.
综上所述,∠OMA=∠OMB.
培优精练
【解析】(1)由圆C:(x-1)2+y2=16,可得圆心坐标为C(1,0),半径r=4,
如图所示,线段AF的垂直平分线交AC于点P,
所以|PF|+|PC|=|PA|+|PC|=4>|FC|=2,
根据椭圆的定义,可知点P的轨迹是以F,C为焦点的椭圆,且2a=4,2c=2,
可得a=2,c=1,则b==,
所以动点P的轨迹方程为+=1.
(2)由题意知直线l的斜率不为0.
当直线l与x轴垂直时,无交点M,N,舍去.
当直线l与x轴不重合也不垂直时,设直线l的方程为y=k(x-3),且k≠0,
由整理得(3+4k2)x2-24k2x+36k2-12=0,由Δ>0,解得-
根据椭圆的对称性,不妨令点M,N在x轴上方,且x2>x1,
假设存在T(t,0),使得∠MTO=∠NTB恒成立,即tan∠MTO=tan∠NTB恒成立,显然x1
又由+=,
得t(y1+y2)-x1y2-x2y1=0,
所以t======,
所以存在点T,0,使得∠MTO=∠NTB恒成立.
考向3 切线、切点弦方程
典例4 (1)A (2)A (3)ABD
【解析】(1)(法一)设A(x1,y1),由x2=4y,得p=2,所以抛物线的准线方程为y=-1.
由抛物线的定义可得|AF|=y1+1=4,得y1=3,代入x2=4y,得x1=±2,
又点A在第一象限,所以x1=2,所以点A的坐标为(2,3),
所以抛物线C:x2=4y在点A处的切线方程为2x=2(y+3),即x-y-3=0.
(法二)同法一得A(2,3),由x2=4y,得y=x2,所以y'=x,所以抛物线C在点A处的切线方程的斜率为×2=,
所以抛物线C在点A处的切线方程为y-3=(x-2),即x-y-3=0.
(2)(法一)因为抛物线C:y2=2px(p>0)上的一点D(x0,y0)处的切线方程为y0y=p(x+x0),即y0y=px+,整理可得y-x-=0,又由题意知该切线方程为y-x-1=0,所以可得y0=p=2,故C的方程为y2=4x.
如图,设点A(x1,y1),B(x2,y2),则M,,点M到y轴的距离d==-1=-1≥-1=2,
当且仅当线段AB经过点F时,等号成立.故AB的中点M到y轴的距离的取值范围为[2,+∞).
(法二)依题意知,切线的斜率为1,故切点必在第一象限,设切点为(x0,y0)(x0>0,y0>0),即,y0,由y=求导可得y'=,
则=1,即=1,化简得y0=p,故切点为,p,代入y-x-1=0中,解得p=2,故C的方程为y2=4x.
以下同法一,可得AB的中点M到y轴的距离的取值范围为[2,+∞).
(3)设M(x1,y1),N(x2,y2),
则过点M的切线方程为y1y=2(x1+x),过点N的切线方程为y2y=2(x2+x),
由题意知这两条切线交于点P(x0,y0),则
从而直线MN的方程为y0y=2(x0+x).
若x0=-1,则直线MN经过点F(1,0),A正确.
因为点M,N在C2上,所以
所以由
解得y=,
即y0=,从而x0=,即P,.
因为H为线段MN的中点,所以H,,
所以PH⊥y轴,B正确.
因为点H,,==-x0=,=y0,
所以点H的轨迹方程为y2=x(x≠0),C错误.
因为=(x0-1,y0),=(x1-1,y1),=(x2-1,y2),
所以·=(x0-1,y0)·(x1-1,y1)=x0x1-x1-x0+1+y0y1=x0x1-x1-x0+1+2(x0+x1)=(x0+1)(x1+1).
又|MF|=x1+1,所以cos ∠PFM==,
同理可得cos ∠PFN=,从而∠PFM=∠PFN,D正确.故选ABD.
培优精练
1.D
【解析】设直线与抛物线x2=2y相切的切点坐标为t,t2,由y=x2求导得y'=x,
因此抛物线x2=2y在点t,t2处的切线方程为y-t2=t(x-t),即tx-y-t2=0,
依题意,此切线与圆x2+(y+1)2=1相切,于是=1,解得t=0或t=±2,所以所求切线的条数为3.故选D.
2.BCD
【解析】对于A,由得x2+(2m-8)x+m2=0,
由Δ=(2m-8)2-4m2=0,解得m=2,故A错误;
对于B,由m=2,得x2-4x+4=0,故x=2,y=2+2=4,故P点坐标为(2,4),
设lPA:y=k(x-2)+4,则lPB:y=-k(x-2)+4,k≠0,
联立lPA与抛物线的方程,得消去x可得ky2-8y+32-16k=0,
Δ=64-4k(32-16k)=64(k-1)2>0,即k≠1,则有yA+4=,即yA=-4,
同理可得yB=--4,故==-4,故B正确;
对于C,kAB=====-1,故C正确;
对于D,由题意可得kPM====,
同理可得kPN=,则kPM·kPN=·=,
联立lMN与抛物线的方程,得消去x可得y2-4y-16=0,
故yM+yN=4,yMyN=-16,
即有kPM·kPN===4,故D正确.故选BCD.
3.解析 (1)由题意得解得
所以椭圆C的方程为+=1.
(2)直线l2与直线OG平行.证明如下:
显然直线l1的斜率存在,设直线l1的方程为y+=m(x+1).
由得(4m2+1)x2+(8m2-12m)x+4m2-12m+1=0.
因为直线l1与椭圆相切,
所以Δ=(8m2-12m)2-4(4m2+1)(4m2-12m+1)=4(28m2+12m-1)=0,
解得m=-或m=.
因为直线l1与椭圆相切于第三象限内的点G,所以m=-,所以2x2+8x+8=0,xG=-2,
所以yG=-(xG+1)-=-1,
所以点G的坐标为(-2,-1),直线OG的斜率为,|PG|2=.
当直线l2的斜率不存在时,|PM||PN|=,所以|PG|2≠|PM|·|PN|.
当直线l2的斜率存在时,设直线l2的方程为y+=k(x+1),M(x1,y1),N(x2,y2).
由得(4k2+1)x2+(8k2-12k)x+4k2-12k+1=0,
直线l2交椭圆C于M,N两点,Δ=4(28k2+12k-1)>0,
所以k<-或k>,所以x1+x2=,x1x2=.
|PM|==|x1+1|,同理得|PN|=|x2+1|,
所以|PM|·|PN|=(1+k2)|x1+1||x2+1|=(1+k2)|x1x2+(x1+x2)+1|=(1+k2).
所以(1+k2)=,解得k=或k=-,
又k<-或k>,所以k=,所以直线l2与直线OG平行.
同课章节目录
