【高考题型分类突破】微专题02 立体几何中的动态问题 2025年高考数学二轮专题复习 学案(含答案)
文档属性
| 名称 | 【高考题型分类突破】微专题02 立体几何中的动态问题 2025年高考数学二轮专题复习 学案(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 221.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-14 00:00:00 | ||
图片预览




文档简介
微专题02 立体几何中的动态问题
立体几何中的动态问题是指空间图形中的某些点、线、面的位置是不确定的,是一类可变的开放性问题.由于位置的不确定性,学生在解题时容易遇到困难,常规的思考方式和解题方法可能不太适用.这类问题要求学生具备较强的空间想象能力和灵活的思维转换能力,能够多角度分析问题.
最值(范围)问题
典例1如图所示,在三棱锥P-ABC中,BC⊥平面PAC,PA⊥AB,PA=AB=4,且E为PB的中点,AF⊥PC于点F,当AC变化时,三棱锥P-AEF体积的最大值是( ).
A. B. C. D.
方法总结:
将待解决的立体几何中的最值问题转化为一个变量或多个变量的函数问题,借助函数求最值的方法来解决立体几何中的最值问题.此外,用变量表示出立体几何中待求的问题后,也常利用基本不等式的方法加以解决.
已知正方体ABCD-A1B1C1D1的棱长为2,P为线段C1D1上的动点,则三棱锥P-BCD的外接球半径的取值范围为( ).
A.,2 B.,
C., D.,
翻折问题
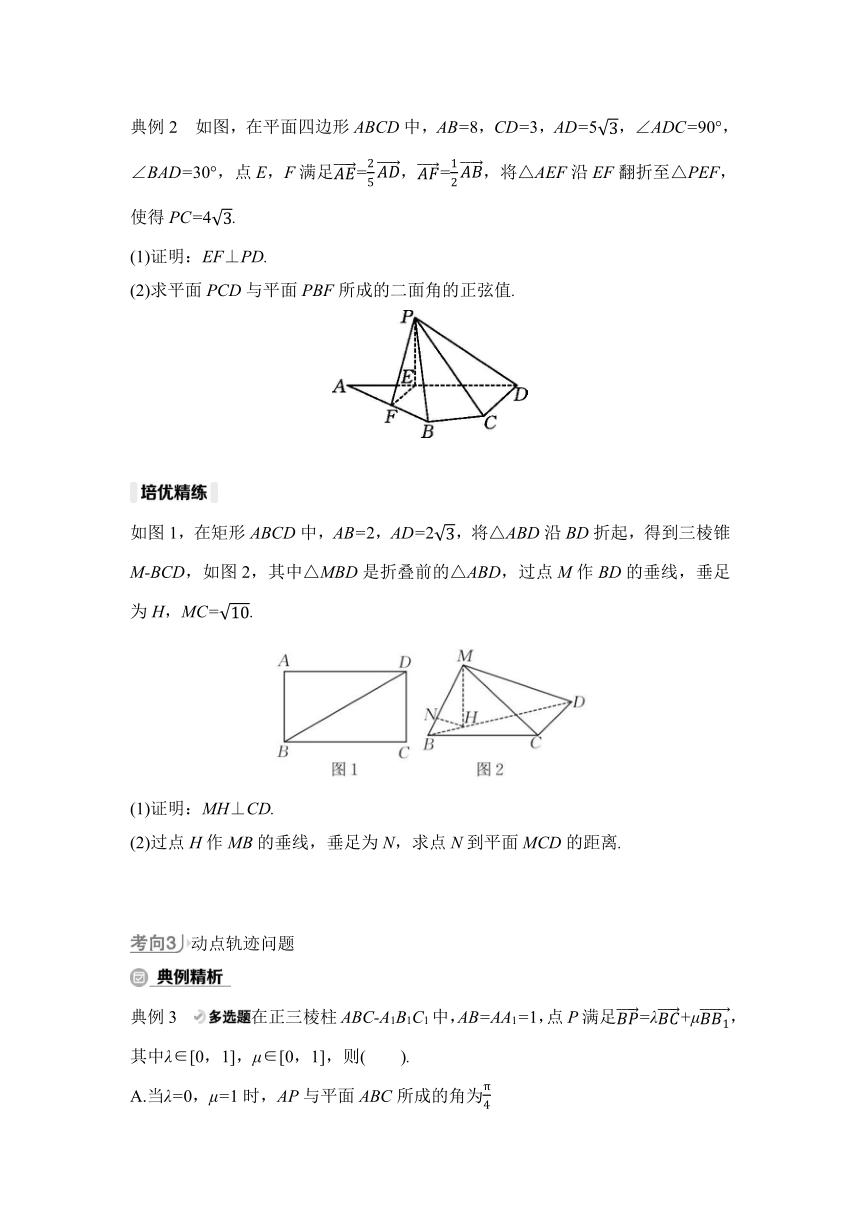
典例2 如图,在平面四边形ABCD中,AB=8,CD=3,AD=5,∠ADC=90°,∠BAD=30°,点E,F满足=,=,将△AEF沿EF翻折至△PEF,使得PC=4.
(1)证明:EF⊥PD.
(2)求平面PCD与平面PBF所成的二面角的正弦值.
如图1,在矩形ABCD中,AB=2,AD=2,将△ABD沿BD折起,得到三棱锥M-BCD,如图2,其中△MBD是折叠前的△ABD,过点M作BD的垂线,垂足为H,MC=.
(1)证明:MH⊥CD.
(2)过点H作MB的垂线,垂足为N,求点N到平面MCD的距离.
动点轨迹问题
典例3 在正三棱柱ABC-A1B1C1中,AB=AA1=1,点P满足=λ+μ,其中λ∈[0,1],μ∈[0,1],则( ).
A.当λ=0,μ=1时,AP与平面ABC所成的角为
B.当λ=时,有且仅有一个点P,使得A1P⊥BP
C.当λ=1,μ=时,平面AB1P⊥平面A1AB
D.若AP=1,则点P的轨迹长度为
方法总结:
方法总结:
(1)几何法:根据平面图形的性质判定.
(2)定义法:转化为平面轨迹问题,用圆锥曲线的定义判定或用代数法计算.
(3)特殊值法:根据空间图形线段的长度关系取特殊值或特殊位置排除.
已知P是边长为1的正方体ABCD-A1B1C1D1表面上的动点,若直线AP与平面ABCD所成角的大小为,则点P的轨迹长度为( ).
A.3
B.2+π
C.(4+π)
D.2+
参考答案
微专题02 立体几何中的动态问题
考向1 最值(范围)问题
典例1 C
【解析】在三棱锥P-ABC中,由BC⊥平面PAC,得BC⊥AC.
又AB=4,所以AC2+BC2=AB2=16.
由题意可知V三棱锥P-AEF=V三棱锥E-PAF=·S△PAF·.
因为BC⊥平面PAC,PA 平面PAC,所以BC⊥PA.又PA⊥AB,AB∩BC=B,AB,BC 平面ABC,所以PA⊥平面ABC,所以PA⊥AC.
又AF⊥PC,所以△PAF∽△PCA,
所以==.
又S△PCA=·AC·PA,PA=4,
所以S△PAF=,
所以V三棱锥E-PAF=·.
设AC=a,0所以V三棱锥E-PAF=·.
令m=a2+16,易知16令x=,则x∈,,
所以V三棱锥E-PAF=·,
令f(x)=-512x2+48x-1由二次函数f(x)=-512x2+48x-1的性质知,当x=时,f(x)有最大值,最大值为,
所以V三棱锥E-PAF的最大值为×=,故三棱锥P-AEF体积的最大值是.故选C.
培优精练 C
【解析】
如图,连接AC,BD,且AC交BD于点E,易得E为△BCD的外心,连接A1C1,B1D1,且A1C1交B1D1于点F,连接EF,易知EF⊥平面BCD,∴三棱锥P-BCD的外接球的球心O在EF上.
设△PCD的外接圆的圆心为O',连接CO',CO,OO',则OO'⊥平面PCD.由正方体ABCD-A1B1C1D1中的棱BC⊥平面CC1D1D,得OO'∥BC.
又E,F分别是BD,B1D1的中点,∴OO'=1.
设△PCD的外接圆半径为r,三棱锥P-BCD的外接球半径为R,则R2=1+r2.
设PC1=x,x∈[0,2],则S△PCD=2=PC·PDsin∠CPD,
∴==.
又r==,
∴r2=.
设f(x)=(x2-4x+8)(x2+4),x∈[0,2],
则f'(x)=4(x3-3x2+6x-4).
设g(x)=f'(x),则g'(x)=12(x2-2x+2)>0,
∴f'(x)在[0,2]上单调递增,又f'(1)=0,
∴f(x)在[0,1]上单调递减,在[1,2]上单调递增.
又f(1)=25,f(0)=f(2)=32,
∴f(x)∈[25,32],∴r2∈,2,
∴R=∈,.故选C.
考向2 翻折问题
典例2
【解析】(1)由AB=8,AD=5,=,=,得AE=2,AF=4.
因为∠BAD=30°,所以在△AEF中,由余弦定理,得EF2=AE2+AF2-2AE·AFcos∠BAD=12+16-2×2×4×=4,所以AE2+EF2=AF2,所以AE⊥EF,即EF⊥AD,所以EF⊥PE,EF⊥DE.
又PE∩DE=E,且PE,DE 平面PDE,所以EF⊥平面PDE.又PD 平面PDE,所以EF⊥PD.
(2)连接CE,由∠ADC=90°,ED=3,CD=3,得CE2=ED2+CD2=36,所以CE=6.
在△PEC中,PC=4,PE=2,EC=6,故EC2+PE2=PC2,所以PE⊥EC.
由(1)知PE⊥EF,又EC∩EF=E,EC,EF 平面ABCD,所以PE⊥平面ABCD.
又ED 平面ABCD,所以PE⊥ED,则PE,EF,ED两两垂直,建立如图所示的空间直角坐标系,
则E(0,0,0),P(0,0,2),D(0,3,0),C(3,3,0),F(2,0,0),A(0,-2,0).由F是AB的中点,得B(4,2,0),所以=(3,3,-2),=(0,3,-2),=(4,2,-2),=(2,0,-2).
设平面PCD和平面PBF的法向量分别为n=(x1,y1,z1),m=(x2,y2,z2),
则
令y1=2,x2=,得x1=0,z1=3,y2=-1,z2=1,所以n=(0,2,3)是平面PCD的一个法向量,m=(,-1,1)是平面PBF的一个法向量,
所以|cos|===.
设平面PCD和平面PBF所成的二面角的平面角为θ,则sin θ==,即平面PCD与平面PBF所成的二面角的正弦值为.
培优精练
【解析】
(1)如图,连接CH.由MB=CD=2,MD=BC=2,∠BMD=∠BCD=90°,得BD=4,∠MDB=∠DBC=30°,MH=,BH=1.
在△BCH中,由余弦定理,得CH==.
因为MH2+CH2=10=MC2,所以MH⊥CH.
又MH⊥BD,CH∩BD=H,CH,BD 平面BCD,所以MH⊥平面BCD.
又CD 平面BCD,所以MH⊥CD.
(2)在△MBD中,由NH⊥MB,MD⊥MB,得NH∥MD.因为MD 平面MCD,NH 平面MCD,所以NH∥平面MCD,所以点N到平面MCD的距离等于点H到平面MCD的距离.设点B到平面MCD的距离为h,点H到平面MCD的距离为d.
因为==,所以d=h.
又cos∠MDC==,所以sin∠MDC=,S△MCD=×2×2×=,S△BCD=×2×2=2.
由V三棱锥B-MCD=V三棱锥M-BCD,得S△MCD·h=S△BCD·MH,即h=2×,解得h=.
所以点N到平面MCD的距离d=h=.
考向3 动点轨迹问题
典例3 ACD
【解析】
如图1,当λ=0,μ=1时,点P与点B1重合,由已知得B1B⊥平面ABC,所以∠B1AB就是AP与平面ABC所成的角,因为AB=AA1=1,所以tan∠B1AB==1,又∠B1AB∈0,,所以∠B1AB=,即AP与平面ABC所成的角为,故A正确.
当λ=时,取线段BC,B1C1的中点分别为M,M1,连接MM1,如图2,因为=+μ,即=μ,所以∥,则点P在线段MM1上,设MP=x(0≤x≤1),则PM1=1-x,
则BP2=BM2+MP2=2+x2,A1P2=A1+P=+(1-x)2,A1B2=2,
若A1P⊥BP,则A1B2=BP2+A1P2,则2=+x2++(1-x)2,整理得x(x-1)=0,解得x=1或x=0,则当点P与点M或M1重合时,A1P⊥BP,即当λ=时,存在两个点P,使得A1P⊥BP,故B错误.
当λ=1,μ=时,=+,则=,所以P是CC1的中点,取BC的中点为Q,B1C1的中点为H,以Q为原点,QA,QB,QH所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,如图3,则A,0,0,B0,,0,B10,,1,P0,-,,
所以=-,,0,==(0,0,1),=-,,1,=-,-,.
设平面A1AB和平面AB1P的法向量分别为m=(x1,y1,z1),n=(x2,y2,z2),
则
令x1=1,z2=2,可得m=(1,,0)是平面A1AB的一个法向量,n=(,-1,2)是平面AB1P的一个法向量.
因为m·n=-=0,所以m⊥n,即平面AB1P⊥平面A1AB,故C正确.
因为AP=1,且=λ+μ,λ∈[0,1],μ∈[0,1],所以点P在侧面BCC1B1上,
由选项C分析可知,AQ⊥平面BCC1B1,AQ=,所以点P的轨迹是以Q为圆心,为半径的半圆,轨迹长度为,故D正确.故选ACD.
培优精练 D
【解析】
若点P在正方形A1B1C1D1内,过点P作PP'⊥平面ABCD,交点为P',连接AP',A1P,如图1,
则∠PAP'为直线AP与平面ABCD所成的角,则∠PAP'=,又PP'=1,所以PA=,所以PA1=1,则点P的轨迹为以A1为圆心,1为半径的部分圆(落在正方形A1B1C1D1内的部分).
若点P在正方形ABB1A1内或正方形ADD1A1内,轨迹分别为线段AB1和AD1,因为点P不可能落在其他三个正方形内,所以点P的轨迹如图2所示.
故点P的轨迹长度为2+×2π×1=2+.
立体几何中的动态问题是指空间图形中的某些点、线、面的位置是不确定的,是一类可变的开放性问题.由于位置的不确定性,学生在解题时容易遇到困难,常规的思考方式和解题方法可能不太适用.这类问题要求学生具备较强的空间想象能力和灵活的思维转换能力,能够多角度分析问题.
最值(范围)问题
典例1如图所示,在三棱锥P-ABC中,BC⊥平面PAC,PA⊥AB,PA=AB=4,且E为PB的中点,AF⊥PC于点F,当AC变化时,三棱锥P-AEF体积的最大值是( ).
A. B. C. D.
方法总结:
将待解决的立体几何中的最值问题转化为一个变量或多个变量的函数问题,借助函数求最值的方法来解决立体几何中的最值问题.此外,用变量表示出立体几何中待求的问题后,也常利用基本不等式的方法加以解决.
已知正方体ABCD-A1B1C1D1的棱长为2,P为线段C1D1上的动点,则三棱锥P-BCD的外接球半径的取值范围为( ).
A.,2 B.,
C., D.,
翻折问题
典例2 如图,在平面四边形ABCD中,AB=8,CD=3,AD=5,∠ADC=90°,∠BAD=30°,点E,F满足=,=,将△AEF沿EF翻折至△PEF,使得PC=4.
(1)证明:EF⊥PD.
(2)求平面PCD与平面PBF所成的二面角的正弦值.
如图1,在矩形ABCD中,AB=2,AD=2,将△ABD沿BD折起,得到三棱锥M-BCD,如图2,其中△MBD是折叠前的△ABD,过点M作BD的垂线,垂足为H,MC=.
(1)证明:MH⊥CD.
(2)过点H作MB的垂线,垂足为N,求点N到平面MCD的距离.
动点轨迹问题
典例3 在正三棱柱ABC-A1B1C1中,AB=AA1=1,点P满足=λ+μ,其中λ∈[0,1],μ∈[0,1],则( ).
A.当λ=0,μ=1时,AP与平面ABC所成的角为
B.当λ=时,有且仅有一个点P,使得A1P⊥BP
C.当λ=1,μ=时,平面AB1P⊥平面A1AB
D.若AP=1,则点P的轨迹长度为
方法总结:
方法总结:
(1)几何法:根据平面图形的性质判定.
(2)定义法:转化为平面轨迹问题,用圆锥曲线的定义判定或用代数法计算.
(3)特殊值法:根据空间图形线段的长度关系取特殊值或特殊位置排除.
已知P是边长为1的正方体ABCD-A1B1C1D1表面上的动点,若直线AP与平面ABCD所成角的大小为,则点P的轨迹长度为( ).
A.3
B.2+π
C.(4+π)
D.2+
参考答案
微专题02 立体几何中的动态问题
考向1 最值(范围)问题
典例1 C
【解析】在三棱锥P-ABC中,由BC⊥平面PAC,得BC⊥AC.
又AB=4,所以AC2+BC2=AB2=16.
由题意可知V三棱锥P-AEF=V三棱锥E-PAF=·S△PAF·.
因为BC⊥平面PAC,PA 平面PAC,所以BC⊥PA.又PA⊥AB,AB∩BC=B,AB,BC 平面ABC,所以PA⊥平面ABC,所以PA⊥AC.
又AF⊥PC,所以△PAF∽△PCA,
所以==.
又S△PCA=·AC·PA,PA=4,
所以S△PAF=,
所以V三棱锥E-PAF=·.
设AC=a,0
令m=a2+16,易知16
所以V三棱锥E-PAF=·,
令f(x)=-512x2+48x-1
所以V三棱锥E-PAF的最大值为×=,故三棱锥P-AEF体积的最大值是.故选C.
培优精练 C
【解析】
如图,连接AC,BD,且AC交BD于点E,易得E为△BCD的外心,连接A1C1,B1D1,且A1C1交B1D1于点F,连接EF,易知EF⊥平面BCD,∴三棱锥P-BCD的外接球的球心O在EF上.
设△PCD的外接圆的圆心为O',连接CO',CO,OO',则OO'⊥平面PCD.由正方体ABCD-A1B1C1D1中的棱BC⊥平面CC1D1D,得OO'∥BC.
又E,F分别是BD,B1D1的中点,∴OO'=1.
设△PCD的外接圆半径为r,三棱锥P-BCD的外接球半径为R,则R2=1+r2.
设PC1=x,x∈[0,2],则S△PCD=2=PC·PDsin∠CPD,
∴==.
又r==,
∴r2=.
设f(x)=(x2-4x+8)(x2+4),x∈[0,2],
则f'(x)=4(x3-3x2+6x-4).
设g(x)=f'(x),则g'(x)=12(x2-2x+2)>0,
∴f'(x)在[0,2]上单调递增,又f'(1)=0,
∴f(x)在[0,1]上单调递减,在[1,2]上单调递增.
又f(1)=25,f(0)=f(2)=32,
∴f(x)∈[25,32],∴r2∈,2,
∴R=∈,.故选C.
考向2 翻折问题
典例2
【解析】(1)由AB=8,AD=5,=,=,得AE=2,AF=4.
因为∠BAD=30°,所以在△AEF中,由余弦定理,得EF2=AE2+AF2-2AE·AFcos∠BAD=12+16-2×2×4×=4,所以AE2+EF2=AF2,所以AE⊥EF,即EF⊥AD,所以EF⊥PE,EF⊥DE.
又PE∩DE=E,且PE,DE 平面PDE,所以EF⊥平面PDE.又PD 平面PDE,所以EF⊥PD.
(2)连接CE,由∠ADC=90°,ED=3,CD=3,得CE2=ED2+CD2=36,所以CE=6.
在△PEC中,PC=4,PE=2,EC=6,故EC2+PE2=PC2,所以PE⊥EC.
由(1)知PE⊥EF,又EC∩EF=E,EC,EF 平面ABCD,所以PE⊥平面ABCD.
又ED 平面ABCD,所以PE⊥ED,则PE,EF,ED两两垂直,建立如图所示的空间直角坐标系,
则E(0,0,0),P(0,0,2),D(0,3,0),C(3,3,0),F(2,0,0),A(0,-2,0).由F是AB的中点,得B(4,2,0),所以=(3,3,-2),=(0,3,-2),=(4,2,-2),=(2,0,-2).
设平面PCD和平面PBF的法向量分别为n=(x1,y1,z1),m=(x2,y2,z2),
则
令y1=2,x2=,得x1=0,z1=3,y2=-1,z2=1,所以n=(0,2,3)是平面PCD的一个法向量,m=(,-1,1)是平面PBF的一个法向量,
所以|cos
设平面PCD和平面PBF所成的二面角的平面角为θ,则sin θ==,即平面PCD与平面PBF所成的二面角的正弦值为.
培优精练
【解析】
(1)如图,连接CH.由MB=CD=2,MD=BC=2,∠BMD=∠BCD=90°,得BD=4,∠MDB=∠DBC=30°,MH=,BH=1.
在△BCH中,由余弦定理,得CH==.
因为MH2+CH2=10=MC2,所以MH⊥CH.
又MH⊥BD,CH∩BD=H,CH,BD 平面BCD,所以MH⊥平面BCD.
又CD 平面BCD,所以MH⊥CD.
(2)在△MBD中,由NH⊥MB,MD⊥MB,得NH∥MD.因为MD 平面MCD,NH 平面MCD,所以NH∥平面MCD,所以点N到平面MCD的距离等于点H到平面MCD的距离.设点B到平面MCD的距离为h,点H到平面MCD的距离为d.
因为==,所以d=h.
又cos∠MDC==,所以sin∠MDC=,S△MCD=×2×2×=,S△BCD=×2×2=2.
由V三棱锥B-MCD=V三棱锥M-BCD,得S△MCD·h=S△BCD·MH,即h=2×,解得h=.
所以点N到平面MCD的距离d=h=.
考向3 动点轨迹问题
典例3 ACD
【解析】
如图1,当λ=0,μ=1时,点P与点B1重合,由已知得B1B⊥平面ABC,所以∠B1AB就是AP与平面ABC所成的角,因为AB=AA1=1,所以tan∠B1AB==1,又∠B1AB∈0,,所以∠B1AB=,即AP与平面ABC所成的角为,故A正确.
当λ=时,取线段BC,B1C1的中点分别为M,M1,连接MM1,如图2,因为=+μ,即=μ,所以∥,则点P在线段MM1上,设MP=x(0≤x≤1),则PM1=1-x,
则BP2=BM2+MP2=2+x2,A1P2=A1+P=+(1-x)2,A1B2=2,
若A1P⊥BP,则A1B2=BP2+A1P2,则2=+x2++(1-x)2,整理得x(x-1)=0,解得x=1或x=0,则当点P与点M或M1重合时,A1P⊥BP,即当λ=时,存在两个点P,使得A1P⊥BP,故B错误.
当λ=1,μ=时,=+,则=,所以P是CC1的中点,取BC的中点为Q,B1C1的中点为H,以Q为原点,QA,QB,QH所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,如图3,则A,0,0,B0,,0,B10,,1,P0,-,,
所以=-,,0,==(0,0,1),=-,,1,=-,-,.
设平面A1AB和平面AB1P的法向量分别为m=(x1,y1,z1),n=(x2,y2,z2),
则
令x1=1,z2=2,可得m=(1,,0)是平面A1AB的一个法向量,n=(,-1,2)是平面AB1P的一个法向量.
因为m·n=-=0,所以m⊥n,即平面AB1P⊥平面A1AB,故C正确.
因为AP=1,且=λ+μ,λ∈[0,1],μ∈[0,1],所以点P在侧面BCC1B1上,
由选项C分析可知,AQ⊥平面BCC1B1,AQ=,所以点P的轨迹是以Q为圆心,为半径的半圆,轨迹长度为,故D正确.故选ACD.
培优精练 D
【解析】
若点P在正方形A1B1C1D1内,过点P作PP'⊥平面ABCD,交点为P',连接AP',A1P,如图1,
则∠PAP'为直线AP与平面ABCD所成的角,则∠PAP'=,又PP'=1,所以PA=,所以PA1=1,则点P的轨迹为以A1为圆心,1为半径的部分圆(落在正方形A1B1C1D1内的部分).
若点P在正方形ABB1A1内或正方形ADD1A1内,轨迹分别为线段AB1和AD1,因为点P不可能落在其他三个正方形内,所以点P的轨迹如图2所示.
故点P的轨迹长度为2+×2π×1=2+.
同课章节目录
