核心考点通关 第六章 第3节 与圆有关的计算 学案(含答案)2025年中考数学一轮教材梳理(陕西)
文档属性
| 名称 | 核心考点通关 第六章 第3节 与圆有关的计算 学案(含答案)2025年中考数学一轮教材梳理(陕西) |  | |
| 格式 | docx | ||
| 文件大小 | 225.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-15 18:21:37 | ||
图片预览

文档简介
第3节 与圆有关的计算
(2024.T23(1)考查,3分)
陕西省2024年在压轴题中以填空题的形式考查了一次,上一次考查是在2012年,陕西中考变化很大,对此部分内容仍不可忽视.
【回归教材·过基础】
【知识体系】
【知识清单】
知识点与圆有关的计算 轮考
与圆有关的计算
方法 公式法 直接和差法 构造和差法 等面积转化法
图示
计算 公式 S阴影=S扇形MEN S阴影=S△ABC -S扇形CAD S阴影=S△OBC-S扇形BDO S阴影=S扇形OCD
【真题精粹·重变式】
考向1弧长的计算
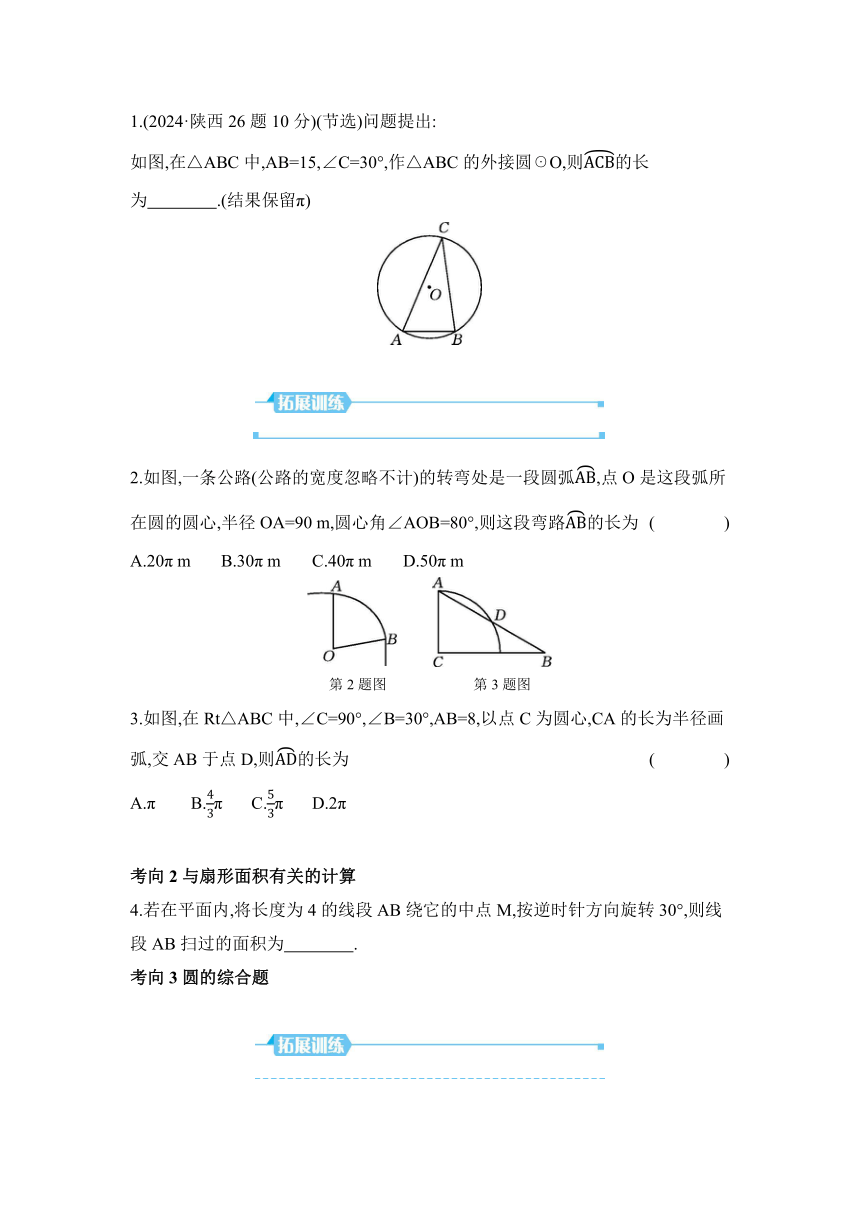
1.(2024·陕西26题10分)(节选)问题提出:
如图,在△ABC中,AB=15,∠C=30°,作△ABC的外接圆☉O,则的长为 .(结果保留π)
2.如图,一条公路(公路的宽度忽略不计)的转弯处是一段圆弧,点O是这段弧所在圆的圆心,半径OA=90 m,圆心角∠AOB=80°,则这段弯路的长为 ( ) A.20π m B.30π m C.40π m D.50π m 第2题图 第3题图 3.如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,以点C为圆心,CA的长为半径画弧,交AB于点D,则的长为 ( ) A.π B.π C.π D.2π
考向2与扇形面积有关的计算
4.若在平面内,将长度为4的线段AB绕它的中点M,按逆时针方向旋转30°,则线段AB扫过的面积为 .
考向3圆的综合题
5.(2023·陕西26题10分)(1)如图1,在△OAB中,OA=OB,∠AOB=120°,AB=24.若☉O的半径为4,点P在☉O上,点M在AB上,连接PM,求线段PM的最小值. (2)如图2,五边形ABCDE是某市工业新区的外环路,新区管委会在点B处,点E处是该市的一个交通枢纽.已知∠A=∠ABC=∠AED=90°,AB=AE=10 000 m,BC=DE=6 000 m.根据新区的自然环境及实际需求,现要在矩形AFDE区域内(含边界)修
一个半径为30 m的圆型环道☉O.过圆心O,作OM⊥AB,垂足为M,与☉O交于点N,连接BN,点P在☉O上,连接PE.其中,线段BN,PE及MN是要修的三条道路,要在所修道路BN,PE之和最短的情况下,使所修道路MN最短,试求此时环道☉O的圆心O到AB的距离OM的长.
参考答案
回归教材·过基础
知识清单
①2πr ② ③πr2 ④
真题精粹·重变式
1.25π 2.C 3.B 4.π
5.解析:(1)如图1,连接OP,OM,过点O作OM'⊥AB,垂足为M',
则OP+PM≥OM.
∵☉O的半径为4,
∴PM≥OM-4≥OM'-4.
∵OA=OB,∠AOB=120°,
∴∠A=30°,
∴OM'=AM'·tan 30°=12tan 30°=4,
∴PM≥OM'-4=4-4,
∴线段PM的最小值为4-4.
(2)如图2,分别在BC,AE上作BB'=AA'=r=30 m,
连接A'B',B'O,OP,OE,B'E.
∵OM⊥AB,BB'⊥AB,ON=BB',
∴四边形BB'ON是平行四边形,
∴BN=B'O.
∵B'O+OP+PE≥B'O+OE≥B'E,
∴BN+PE≥B'E-r,
∴当点O在B'E上时,BN+PE取得最小值.
作☉O',使圆心O'在B'E上,半径r=30 m,
作O'M'⊥AB,垂足为M',并与A'B'交于点H,
∴O'H∥A'E,
∴△B'O'H∽△B'EA',
∴=.
∵☉O'在矩形AFDE区域内(含边界),
∴当☉O'与FD相切时,B'H最短,即B'H=10 000-6 000+30=4 030(m),
此时,O'H也最短.
∵M'N'=O'H,
∴M'N'也最短.
∴O'H==
=4 017.91(m),
∴O'M'=O'H+30=4 047.91(m),
∴此时环道☉O的圆心O到AB的距离OM的长为4 047.91 m.
(2024.T23(1)考查,3分)
陕西省2024年在压轴题中以填空题的形式考查了一次,上一次考查是在2012年,陕西中考变化很大,对此部分内容仍不可忽视.
【回归教材·过基础】
【知识体系】
【知识清单】
知识点与圆有关的计算 轮考
与圆有关的计算
方法 公式法 直接和差法 构造和差法 等面积转化法
图示
计算 公式 S阴影=S扇形MEN S阴影=S△ABC -S扇形CAD S阴影=S△OBC-S扇形BDO S阴影=S扇形OCD
【真题精粹·重变式】
考向1弧长的计算
1.(2024·陕西26题10分)(节选)问题提出:
如图,在△ABC中,AB=15,∠C=30°,作△ABC的外接圆☉O,则的长为 .(结果保留π)
2.如图,一条公路(公路的宽度忽略不计)的转弯处是一段圆弧,点O是这段弧所在圆的圆心,半径OA=90 m,圆心角∠AOB=80°,则这段弯路的长为 ( ) A.20π m B.30π m C.40π m D.50π m 第2题图 第3题图 3.如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,以点C为圆心,CA的长为半径画弧,交AB于点D,则的长为 ( ) A.π B.π C.π D.2π
考向2与扇形面积有关的计算
4.若在平面内,将长度为4的线段AB绕它的中点M,按逆时针方向旋转30°,则线段AB扫过的面积为 .
考向3圆的综合题
5.(2023·陕西26题10分)(1)如图1,在△OAB中,OA=OB,∠AOB=120°,AB=24.若☉O的半径为4,点P在☉O上,点M在AB上,连接PM,求线段PM的最小值. (2)如图2,五边形ABCDE是某市工业新区的外环路,新区管委会在点B处,点E处是该市的一个交通枢纽.已知∠A=∠ABC=∠AED=90°,AB=AE=10 000 m,BC=DE=6 000 m.根据新区的自然环境及实际需求,现要在矩形AFDE区域内(含边界)修
一个半径为30 m的圆型环道☉O.过圆心O,作OM⊥AB,垂足为M,与☉O交于点N,连接BN,点P在☉O上,连接PE.其中,线段BN,PE及MN是要修的三条道路,要在所修道路BN,PE之和最短的情况下,使所修道路MN最短,试求此时环道☉O的圆心O到AB的距离OM的长.
参考答案
回归教材·过基础
知识清单
①2πr ② ③πr2 ④
真题精粹·重变式
1.25π 2.C 3.B 4.π
5.解析:(1)如图1,连接OP,OM,过点O作OM'⊥AB,垂足为M',
则OP+PM≥OM.
∵☉O的半径为4,
∴PM≥OM-4≥OM'-4.
∵OA=OB,∠AOB=120°,
∴∠A=30°,
∴OM'=AM'·tan 30°=12tan 30°=4,
∴PM≥OM'-4=4-4,
∴线段PM的最小值为4-4.
(2)如图2,分别在BC,AE上作BB'=AA'=r=30 m,
连接A'B',B'O,OP,OE,B'E.
∵OM⊥AB,BB'⊥AB,ON=BB',
∴四边形BB'ON是平行四边形,
∴BN=B'O.
∵B'O+OP+PE≥B'O+OE≥B'E,
∴BN+PE≥B'E-r,
∴当点O在B'E上时,BN+PE取得最小值.
作☉O',使圆心O'在B'E上,半径r=30 m,
作O'M'⊥AB,垂足为M',并与A'B'交于点H,
∴O'H∥A'E,
∴△B'O'H∽△B'EA',
∴=.
∵☉O'在矩形AFDE区域内(含边界),
∴当☉O'与FD相切时,B'H最短,即B'H=10 000-6 000+30=4 030(m),
此时,O'H也最短.
∵M'N'=O'H,
∴M'N'也最短.
∴O'H==
=4 017.91(m),
∴O'M'=O'H+30=4 047.91(m),
∴此时环道☉O的圆心O到AB的距离OM的长为4 047.91 m.
同课章节目录
