核心考点通关 第四章 第6节 解直角三角形及其应用 学案(含答案)2025年中考数学一轮教材梳理(陕西)
文档属性
| 名称 | 核心考点通关 第四章 第6节 解直角三角形及其应用 学案(含答案)2025年中考数学一轮教材梳理(陕西) | 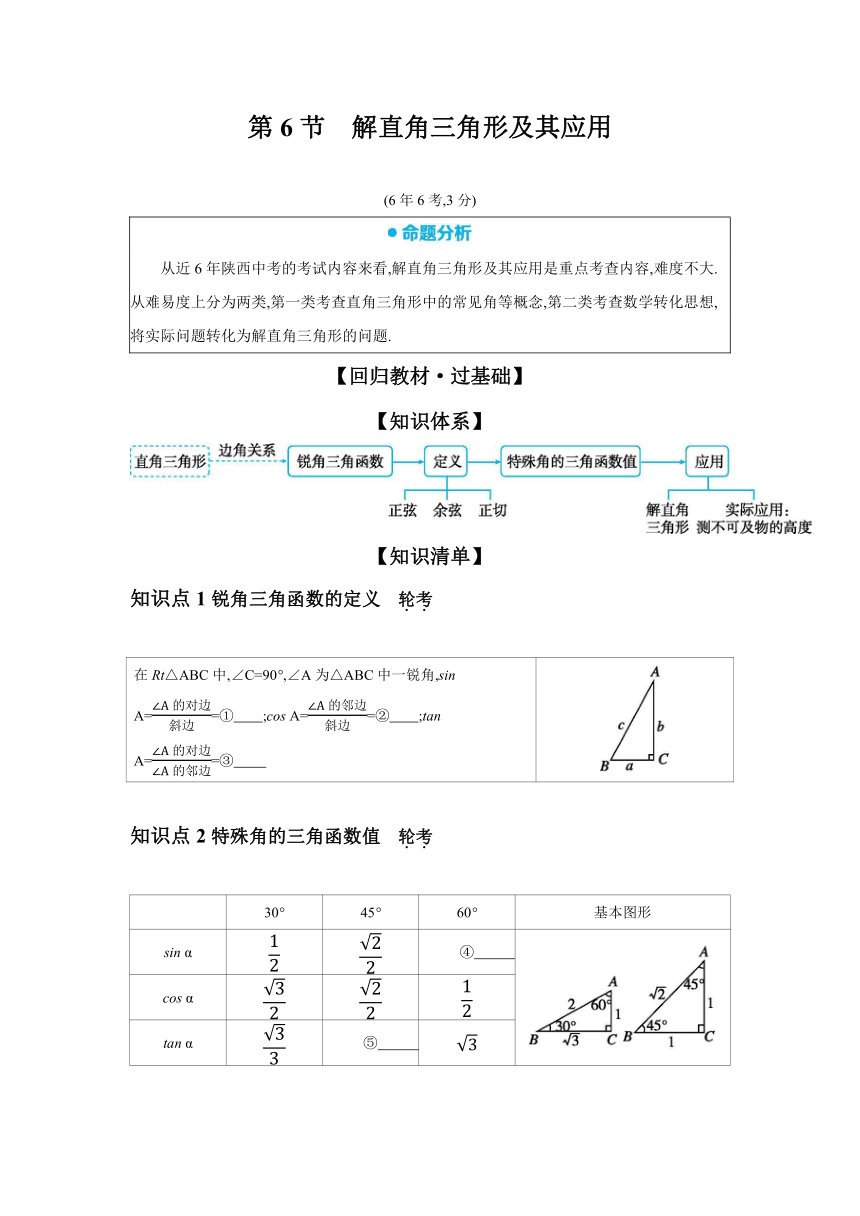 | |
| 格式 | docx | ||
| 文件大小 | 291.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-15 18:29:18 | ||
图片预览


文档简介
第6节 解直角三角形及其应用
(6年6考,3分)
从近6年陕西中考的考试内容来看,解直角三角形及其应用是重点考查内容,难度不大.从难易度上分为两类,第一类考查直角三角形中的常见角等概念,第二类考查数学转化思想,将实际问题转化为解直角三角形的问题.
【回归教材·过基础】
【知识体系】
【知识清单】
知识点1锐角三角函数的定义 轮考
在Rt△ABC中,∠C=90°,∠A为△ABC中一锐角,sin A==① ;cos A==② ;tan A==③
知识点2特殊角的三角函数值 轮考
30° 45° 60° 基本图形
sin α ④
cos α
tan α ⑤
知识点3解直角三角形 常考
【真题精粹·重变式】
考向1特殊角的三角函数值
1.计算:×+4×|1-|sin 60°-.
考向2直角三角形的边角关系 6年3考
2.(2019·陕西6题3分)如图,在△ABC中,∠B=30°,∠C=45°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E.若DE=1,则BC的长为 ( )
A.2+ B.+
C.+2 D.3
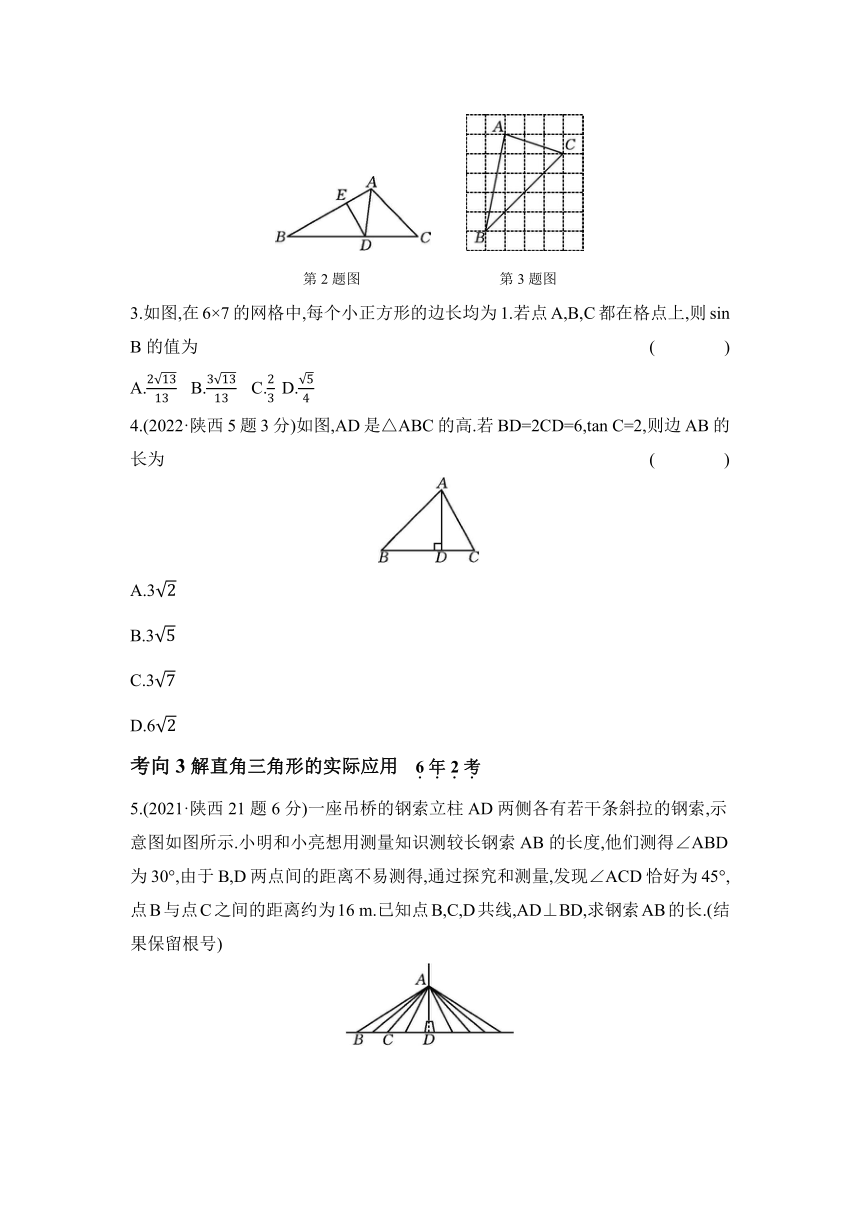
第2题图 第3题图
3.如图,在6×7的网格中,每个小正方形的边长均为1.若点A,B,C都在格点上,则sin B的值为 ( )
A. B. C. D.
4.(2022·陕西5题3分)如图,AD是△ABC的高.若BD=2CD=6,tan C=2,则边AB的长为 ( )
A.3
B.3
C.3
D.6
考向3解直角三角形的实际应用 6年2考
5.(2021·陕西21题6分)一座吊桥的钢索立柱AD两侧各有若干条斜拉的钢索,示意图如图所示.小明和小亮想用测量知识测较长钢索AB的长度,他们测得∠ABD为30°,由于B,D两点间的距离不易测得,通过探究和测量,发现∠ACD恰好为45°,点B与点C之间的距离约为16 m.已知点B,C,D共线,AD⊥BD,求钢索AB的长.(结果保留根号)
6.(2023·陕西21题6分)一天晚上,小明和爸爸带着测角仪和皮尺去公园测量一景观灯(灯杆底部不可到达)的高AB.如图,当小明爸爸站在点D处时,他在该景观灯照射下的影子长为DF,测得DF=2.4 m;当小明站在爸爸影子的顶端F处时,测得点A的仰角
α为26.6°.已知爸爸的身高CD=1.8 m,小明眼睛到地面的距离EF=1.6 m,点F,D,B在同一条直线上,EF⊥FB,CD⊥FB,AB⊥FB.求该景观灯的高AB.(参考数据:sin 26.6°≈0.45,cos 26.6°≈0.89,tan 26.6°≈0.50)
7.(2024·陕西21题6分)如图,一座小山顶的水平观景台的海拔为1 600 m,小明想利用这个观景台测量对面山顶C点处的海拔.他在该观景台上选定了一点A,在点A处测得点C的仰角∠CAE=42°,再在AE上选一点B,在点B处测得点C的仰角α=45°,AB=10 m.求山顶C点处的海拔.(小明身高忽略不计,参考数据:sin 42°≈0.67,cos 42°≈0.74,tan 42°≈0.90)
参考答案
回归教材·过基础
知识清单
① ② ③ ④ ⑤1 ⑥90° ⑦c2 ⑧sin B
⑨ ⑩越陡
真题精粹·重变式
1.解析:原式=2+4×-1×-2
=2+6-2-2
=4.
2.A 3.A 4.D
5.解析:在△ADC中,设AD=x m.
∵AD⊥BD,∠ACD=45°,
∴CD=AD=x.
在△ADB中,AD⊥BD,∠ABD=30°,
∴AD=BDtan 30°,
即x=(16+x),
解得x=8+8,
∴AB=2AD=(16+16)m.
答:钢索AB的长为(16+16)m.
6.解析:
如图,过点E作EH⊥AB,垂足为H,得矩形EFBH.
由题意得EH=FB,EF=BH=1.6 m.
设EH=FB=x m,
在Rt△AEH中,∠AEH=26.6°,
∴AH=EH·tan 26.6°≈0.5x(m),
∴AB=AH+BH=(0.5x+1.6)m.
∵CD⊥FB,AB⊥FB,
∴∠CDF=∠ABF=90°.
∵∠CFD=∠AFB,
∴△CDF∽△ABF,
∴=,
∴=,
∴AB=0.75x,
∴0.75x=0.5x+1.6,
解得x=6.4,
∴AB=0.75x=4.8(m),
∴该景观灯的高AB约为4.8 m.
7.解析:如图,过点C作CD⊥AE,交AE的延长线于点D.
设BD=x m.
∵AB=10 m,∴AD=AB+BD=(x+10)m.
在Rt△BCD中,∠CBD=45°,∴CD=BD·tan 45°=x m.
在Rt△ACD中,∠A=42°,∴CD=AD·tan 42°≈0.9(x+10) m,
∴x=0.9(x+10),解得x=90,∴CD=90 m.
∵小山顶的水平观景台的海拔为1 600 m,
∴山顶C点处的海拔约为1 600+90=1 690(m).
(6年6考,3分)
从近6年陕西中考的考试内容来看,解直角三角形及其应用是重点考查内容,难度不大.从难易度上分为两类,第一类考查直角三角形中的常见角等概念,第二类考查数学转化思想,将实际问题转化为解直角三角形的问题.
【回归教材·过基础】
【知识体系】
【知识清单】
知识点1锐角三角函数的定义 轮考
在Rt△ABC中,∠C=90°,∠A为△ABC中一锐角,sin A==① ;cos A==② ;tan A==③
知识点2特殊角的三角函数值 轮考
30° 45° 60° 基本图形
sin α ④
cos α
tan α ⑤
知识点3解直角三角形 常考
【真题精粹·重变式】
考向1特殊角的三角函数值
1.计算:×+4×|1-|sin 60°-.
考向2直角三角形的边角关系 6年3考
2.(2019·陕西6题3分)如图,在△ABC中,∠B=30°,∠C=45°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E.若DE=1,则BC的长为 ( )
A.2+ B.+
C.+2 D.3
第2题图 第3题图
3.如图,在6×7的网格中,每个小正方形的边长均为1.若点A,B,C都在格点上,则sin B的值为 ( )
A. B. C. D.
4.(2022·陕西5题3分)如图,AD是△ABC的高.若BD=2CD=6,tan C=2,则边AB的长为 ( )
A.3
B.3
C.3
D.6
考向3解直角三角形的实际应用 6年2考
5.(2021·陕西21题6分)一座吊桥的钢索立柱AD两侧各有若干条斜拉的钢索,示意图如图所示.小明和小亮想用测量知识测较长钢索AB的长度,他们测得∠ABD为30°,由于B,D两点间的距离不易测得,通过探究和测量,发现∠ACD恰好为45°,点B与点C之间的距离约为16 m.已知点B,C,D共线,AD⊥BD,求钢索AB的长.(结果保留根号)
6.(2023·陕西21题6分)一天晚上,小明和爸爸带着测角仪和皮尺去公园测量一景观灯(灯杆底部不可到达)的高AB.如图,当小明爸爸站在点D处时,他在该景观灯照射下的影子长为DF,测得DF=2.4 m;当小明站在爸爸影子的顶端F处时,测得点A的仰角
α为26.6°.已知爸爸的身高CD=1.8 m,小明眼睛到地面的距离EF=1.6 m,点F,D,B在同一条直线上,EF⊥FB,CD⊥FB,AB⊥FB.求该景观灯的高AB.(参考数据:sin 26.6°≈0.45,cos 26.6°≈0.89,tan 26.6°≈0.50)
7.(2024·陕西21题6分)如图,一座小山顶的水平观景台的海拔为1 600 m,小明想利用这个观景台测量对面山顶C点处的海拔.他在该观景台上选定了一点A,在点A处测得点C的仰角∠CAE=42°,再在AE上选一点B,在点B处测得点C的仰角α=45°,AB=10 m.求山顶C点处的海拔.(小明身高忽略不计,参考数据:sin 42°≈0.67,cos 42°≈0.74,tan 42°≈0.90)
参考答案
回归教材·过基础
知识清单
① ② ③ ④ ⑤1 ⑥90° ⑦c2 ⑧sin B
⑨ ⑩越陡
真题精粹·重变式
1.解析:原式=2+4×-1×-2
=2+6-2-2
=4.
2.A 3.A 4.D
5.解析:在△ADC中,设AD=x m.
∵AD⊥BD,∠ACD=45°,
∴CD=AD=x.
在△ADB中,AD⊥BD,∠ABD=30°,
∴AD=BDtan 30°,
即x=(16+x),
解得x=8+8,
∴AB=2AD=(16+16)m.
答:钢索AB的长为(16+16)m.
6.解析:
如图,过点E作EH⊥AB,垂足为H,得矩形EFBH.
由题意得EH=FB,EF=BH=1.6 m.
设EH=FB=x m,
在Rt△AEH中,∠AEH=26.6°,
∴AH=EH·tan 26.6°≈0.5x(m),
∴AB=AH+BH=(0.5x+1.6)m.
∵CD⊥FB,AB⊥FB,
∴∠CDF=∠ABF=90°.
∵∠CFD=∠AFB,
∴△CDF∽△ABF,
∴=,
∴=,
∴AB=0.75x,
∴0.75x=0.5x+1.6,
解得x=6.4,
∴AB=0.75x=4.8(m),
∴该景观灯的高AB约为4.8 m.
7.解析:如图,过点C作CD⊥AE,交AE的延长线于点D.
设BD=x m.
∵AB=10 m,∴AD=AB+BD=(x+10)m.
在Rt△BCD中,∠CBD=45°,∴CD=BD·tan 45°=x m.
在Rt△ACD中,∠A=42°,∴CD=AD·tan 42°≈0.9(x+10) m,
∴x=0.9(x+10),解得x=90,∴CD=90 m.
∵小山顶的水平观景台的海拔为1 600 m,
∴山顶C点处的海拔约为1 600+90=1 690(m).
同课章节目录
