2024-2025学年人教版数学九年级上册期末培优训练(含答案)
文档属性
| 名称 | 2024-2025学年人教版数学九年级上册期末培优训练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 490.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-16 14:32:36 | ||
图片预览



文档简介
2024-2025学年人教版数学九年级上册期末培优训练
一、单选题(共10题;共30分)
1.(3分)如果关于的方程无实数根,则的取值范围是( )
A. B.且 C. D.且
2.(3分)在平面直角坐标系中,以点为圆心,3为半径的圆( )
A.与x轴相交,与y轴相切 B.与x轴相离,与y轴相切
C.与x轴相离,与y轴相交 D.与x轴相切,与y轴相离
3.(3分)下列说法正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.形如的式子叫做二次根式
C.对角线相等的四边形是矩形
D.关于中心对称的两个图形是全等的
4.(3分)已知直角三角形的两条直角边长恰好是方程的两个根,则此直角三角形斜边长是( )
A.13 B.5 C. D.
5.(3分)如图,四边形 是正方形, ,点 P 为射线 上一点,连接 ,将 绕点 P 顺时针旋转得到线段 ,过 B 作 平行线交 延长线于 F ,设 长为 x ,四边形 的面积为 y ,下列图象能正确反映出 y 与 x 函数关系的是( )
A. B.
C. D.
6.(3分)如图,O是等边内一点,,,,将线段BO以点B为旋转中心逆时针旋转60°得到线段,则的度数为( )
A.100° B.120° C.130° D.150°
7.(3分)下列方程是关于x的一元二次方程的是( )
A.x2+xy+2=0 B. C.x2+x+1=0 D.ax2+bx+c=0
8.(3分)关于二次函数y=x2﹣4m x+3 (m是常数),有以下说法:
①不管m是什么实数,该函数图象的顶点一定在函数y=﹣x2 +3的图象上;②若该函数图象与x轴相交于点(a,0), (b, 0) (aA.①② B.②③ C.①③ D.①②③
9.(3分)已知菱形ABCD的边长为5,两条对角线交于O点,且OA、OB的长分别是关于的方程的根,则m等于( )
A. B. C. D.
10.(3分)如图是二次函数(是常数,)图象的一部分,与轴的交点在点和之间,对称轴是直线.对于下列说法:①;②;③;④(为实数),其中正确的是( )
A.①②④ B.①② C.②③④ D.③④
二、填空题(共7题;共25分)
11.(3分)一个不透明的袋中装有除颜色外均相同的9个红球、3个白球、若干个绿球,每次摇匀后随机摸出一个球,记下颜色后再放回袋中,经过大量重复试验后,发现摸到绿球的频率稳定在0.4,则袋中约有绿球 个.
12.(6分)点与圆的位置关系有点在圆内,点在圆 ,点在圆 三种,可以用点到 的距离和半径的大小关系来判断.
13.(3分)如图,五个半径为2的圆,圆心分别是点A,B,C,D,E,则图中阴影部分的面积和是 .
14.(3分)已知满足,,且,则的值为 .
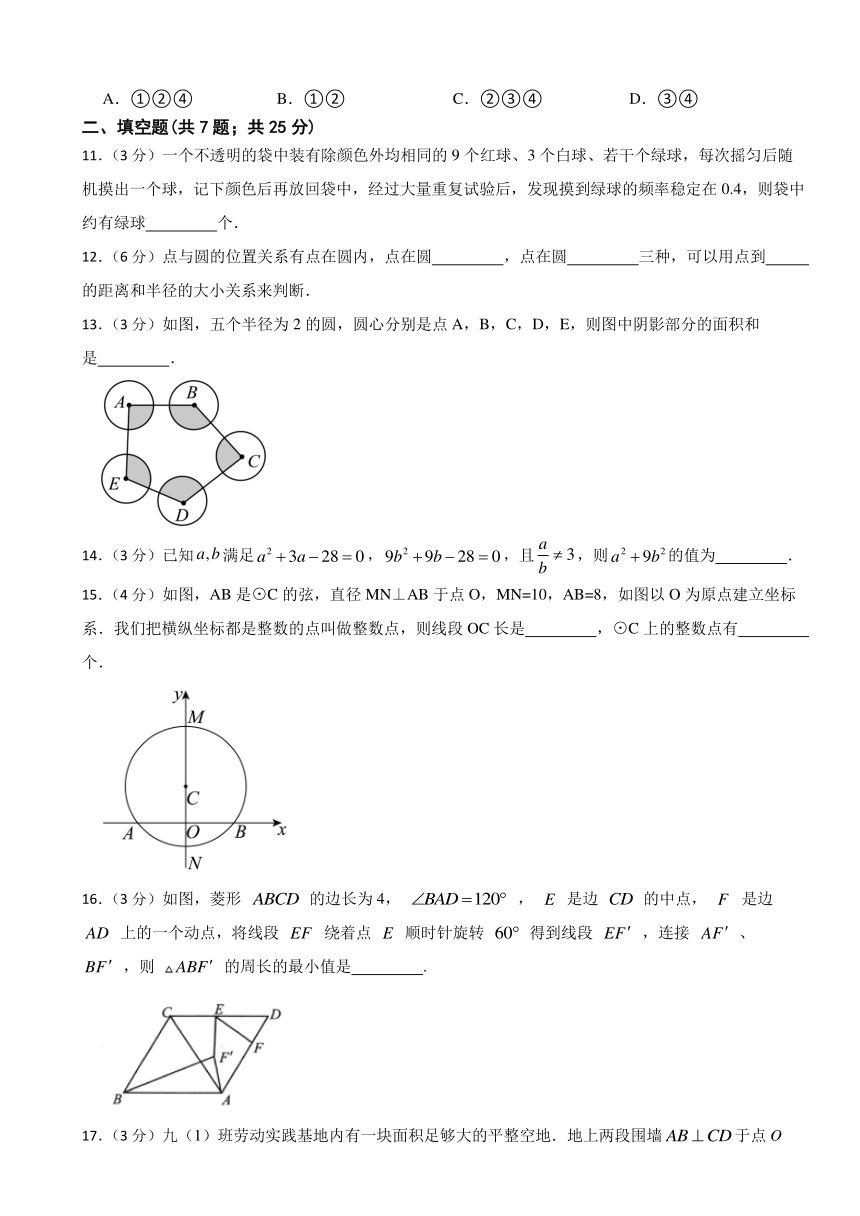
15.(4分)如图,AB是⊙C的弦,直径MN⊥AB于点O,MN=10,AB=8,如图以O为原点建立坐标系.我们把横纵坐标都是整数的点叫做整数点,则线段OC长是 ,⊙C上的整数点有 个.
16.(3分)如图,菱形 的边长为4, , 是边 的中点, 是边 上的一个动点,将线段 绕着点 顺时针旋转 得到线段 ,连接 、 ,则 的周长的最小值是 .
17.(3分)九(1)班劳动实践基地内有一块面积足够大的平整空地.地上两段围墙于点O(如图),其中上的段围墙空缺.同学们测得m,m,m,m,m.班长买来可切断的围栏m,准备利用已有围墙,围出一块封闭的矩形菜地,则该菜地最大面积是 .
三、解答题(共6题;共45分)
18.(6分)已知等腰三角形的一腰和底边的长是关于x的方程的两个实数根.
①时,求的周长;
②当为等边三角形时,求m的值.
19.(7分)不透明的袋子中装有红球、黄球、蓝球各一个,这些球除颜色外无其他差别.
(1)(3分)从袋子中随机摸出一个球,摸到蓝球的概率是___________;
(2)(4分)从袋子中随机摸出一个球后,放回并摇匀,再随机摸出一个球.求两次摸到的球的颜色为“一红一黄”的概率.
20.(7分)已知一元二次方程.
(1)(3分)若方程有两个实数根,求的范围;
(2)(4分)若方程的两个实数根为,,且,求的值.
21.(8分)如图,AB是⊙O的直径,弦CD⊥AB于点E,G是上任意一点,连结AD,AG,GD.
(1)(4分)找出图中与∠G相等的角(不添加其它线),并说明理由;
(2)(4分)若点C是的中点,且CD=AG,求∠G的度数.
22.(8分)如图所示,已知抛物线 y=(x-2)(x+a)(a>0)与x轴交于点A,B,与y轴交于点C,且点A在点B的左侧,连接AC,BC.
(1)(4分)若抛物线过点 M(-2,-2),求实数a的值;
(2)(4分)在(1)的条件下,求出△ABC的面积.
23.(9分)如图1,在平面直角坐标中,抛物线与x轴交于点、两点,与y轴交于点C,连接,直线交y轴于点M.P为直线上方抛物线上一动点,过点P作x轴的垂线,分别交直线、于点E、F.
(1)(3分)求抛物线的表达式;
(2)(3分)当点P落在抛物线的对称轴上时,求的面积;
(3)(3分)若点N为y轴上一动点,当四边形为矩形时,求点N的坐标;
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】D
4.【答案】D
5.【答案】D
6.【答案】D
7.【答案】C
8.【答案】C
9.【答案】A
10.【答案】A
11.【答案】8
12.【答案】上;外;圆心
13.【答案】
14.【答案】65
15.【答案】3;12
16.【答案】
17.【答案】46.4
18.【答案】①;②
19.【答案】(1)
(2)
20.【答案】(1)
(2)
21.【答案】(1)解:和相等的角是.
证明如下:
∵是的直径且,
∴,
∴.
(2)解:连接,
∵,
∴,
∵是的直径且,
∴,则,
∵ 点C是的中点,
∴,
∴,
∴,
∴,
∴,
∴.
22.【答案】(1)解:将(-2,-2)代入抛物线解析式,得(-2-2)(-2+a)=-2,
解得a=4.
(2)解:由(1),知抛物线解析式为y=(x-2)(x+4),
当y=0时,得(x-2)(x+4)=0,
解得x1=2,x2=-4.
∵点A在点B的左侧,
∴点A的坐标为(-4,0),点B的坐标为(2,0).
当x=0时,得y=-2,
∴点C的坐标为(0,-2).
∴S△ABC=×|4-(-2)|×2=6.
23.【答案】(1)
(2)
(3)
一、单选题(共10题;共30分)
1.(3分)如果关于的方程无实数根,则的取值范围是( )
A. B.且 C. D.且
2.(3分)在平面直角坐标系中,以点为圆心,3为半径的圆( )
A.与x轴相交,与y轴相切 B.与x轴相离,与y轴相切
C.与x轴相离,与y轴相交 D.与x轴相切,与y轴相离
3.(3分)下列说法正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.形如的式子叫做二次根式
C.对角线相等的四边形是矩形
D.关于中心对称的两个图形是全等的
4.(3分)已知直角三角形的两条直角边长恰好是方程的两个根,则此直角三角形斜边长是( )
A.13 B.5 C. D.
5.(3分)如图,四边形 是正方形, ,点 P 为射线 上一点,连接 ,将 绕点 P 顺时针旋转得到线段 ,过 B 作 平行线交 延长线于 F ,设 长为 x ,四边形 的面积为 y ,下列图象能正确反映出 y 与 x 函数关系的是( )
A. B.
C. D.
6.(3分)如图,O是等边内一点,,,,将线段BO以点B为旋转中心逆时针旋转60°得到线段,则的度数为( )
A.100° B.120° C.130° D.150°
7.(3分)下列方程是关于x的一元二次方程的是( )
A.x2+xy+2=0 B. C.x2+x+1=0 D.ax2+bx+c=0
8.(3分)关于二次函数y=x2﹣4m x+3 (m是常数),有以下说法:
①不管m是什么实数,该函数图象的顶点一定在函数y=﹣x2 +3的图象上;②若该函数图象与x轴相交于点(a,0), (b, 0) (a
9.(3分)已知菱形ABCD的边长为5,两条对角线交于O点,且OA、OB的长分别是关于的方程的根,则m等于( )
A. B. C. D.
10.(3分)如图是二次函数(是常数,)图象的一部分,与轴的交点在点和之间,对称轴是直线.对于下列说法:①;②;③;④(为实数),其中正确的是( )
A.①②④ B.①② C.②③④ D.③④
二、填空题(共7题;共25分)
11.(3分)一个不透明的袋中装有除颜色外均相同的9个红球、3个白球、若干个绿球,每次摇匀后随机摸出一个球,记下颜色后再放回袋中,经过大量重复试验后,发现摸到绿球的频率稳定在0.4,则袋中约有绿球 个.
12.(6分)点与圆的位置关系有点在圆内,点在圆 ,点在圆 三种,可以用点到 的距离和半径的大小关系来判断.
13.(3分)如图,五个半径为2的圆,圆心分别是点A,B,C,D,E,则图中阴影部分的面积和是 .
14.(3分)已知满足,,且,则的值为 .
15.(4分)如图,AB是⊙C的弦,直径MN⊥AB于点O,MN=10,AB=8,如图以O为原点建立坐标系.我们把横纵坐标都是整数的点叫做整数点,则线段OC长是 ,⊙C上的整数点有 个.
16.(3分)如图,菱形 的边长为4, , 是边 的中点, 是边 上的一个动点,将线段 绕着点 顺时针旋转 得到线段 ,连接 、 ,则 的周长的最小值是 .
17.(3分)九(1)班劳动实践基地内有一块面积足够大的平整空地.地上两段围墙于点O(如图),其中上的段围墙空缺.同学们测得m,m,m,m,m.班长买来可切断的围栏m,准备利用已有围墙,围出一块封闭的矩形菜地,则该菜地最大面积是 .
三、解答题(共6题;共45分)
18.(6分)已知等腰三角形的一腰和底边的长是关于x的方程的两个实数根.
①时,求的周长;
②当为等边三角形时,求m的值.
19.(7分)不透明的袋子中装有红球、黄球、蓝球各一个,这些球除颜色外无其他差别.
(1)(3分)从袋子中随机摸出一个球,摸到蓝球的概率是___________;
(2)(4分)从袋子中随机摸出一个球后,放回并摇匀,再随机摸出一个球.求两次摸到的球的颜色为“一红一黄”的概率.
20.(7分)已知一元二次方程.
(1)(3分)若方程有两个实数根,求的范围;
(2)(4分)若方程的两个实数根为,,且,求的值.
21.(8分)如图,AB是⊙O的直径,弦CD⊥AB于点E,G是上任意一点,连结AD,AG,GD.
(1)(4分)找出图中与∠G相等的角(不添加其它线),并说明理由;
(2)(4分)若点C是的中点,且CD=AG,求∠G的度数.
22.(8分)如图所示,已知抛物线 y=(x-2)(x+a)(a>0)与x轴交于点A,B,与y轴交于点C,且点A在点B的左侧,连接AC,BC.
(1)(4分)若抛物线过点 M(-2,-2),求实数a的值;
(2)(4分)在(1)的条件下,求出△ABC的面积.
23.(9分)如图1,在平面直角坐标中,抛物线与x轴交于点、两点,与y轴交于点C,连接,直线交y轴于点M.P为直线上方抛物线上一动点,过点P作x轴的垂线,分别交直线、于点E、F.
(1)(3分)求抛物线的表达式;
(2)(3分)当点P落在抛物线的对称轴上时,求的面积;
(3)(3分)若点N为y轴上一动点,当四边形为矩形时,求点N的坐标;
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】D
4.【答案】D
5.【答案】D
6.【答案】D
7.【答案】C
8.【答案】C
9.【答案】A
10.【答案】A
11.【答案】8
12.【答案】上;外;圆心
13.【答案】
14.【答案】65
15.【答案】3;12
16.【答案】
17.【答案】46.4
18.【答案】①;②
19.【答案】(1)
(2)
20.【答案】(1)
(2)
21.【答案】(1)解:和相等的角是.
证明如下:
∵是的直径且,
∴,
∴.
(2)解:连接,
∵,
∴,
∵是的直径且,
∴,则,
∵ 点C是的中点,
∴,
∴,
∴,
∴,
∴,
∴.
22.【答案】(1)解:将(-2,-2)代入抛物线解析式,得(-2-2)(-2+a)=-2,
解得a=4.
(2)解:由(1),知抛物线解析式为y=(x-2)(x+4),
当y=0时,得(x-2)(x+4)=0,
解得x1=2,x2=-4.
∵点A在点B的左侧,
∴点A的坐标为(-4,0),点B的坐标为(2,0).
当x=0时,得y=-2,
∴点C的坐标为(0,-2).
∴S△ABC=×|4-(-2)|×2=6.
23.【答案】(1)
(2)
(3)
同课章节目录
