8.3.2 用多种正多边形 课件(共16张PPT)
文档属性
| 名称 | 8.3.2 用多种正多边形 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-17 07:13:07 | ||
图片预览




文档简介
(共16张PPT)
8.3 用正多边形铺设地面
2.用多种正多边形
掌握用多种正多边形拼成平面的规律及其运用.(重点)
1.在正三角形、正方形、正五边形、正六边形、正八边形中取一种,可以铺满地板的有哪些?
2.用同种正多边形瓷砖能不留空隙,不重叠地铺满地板的关键是什么?
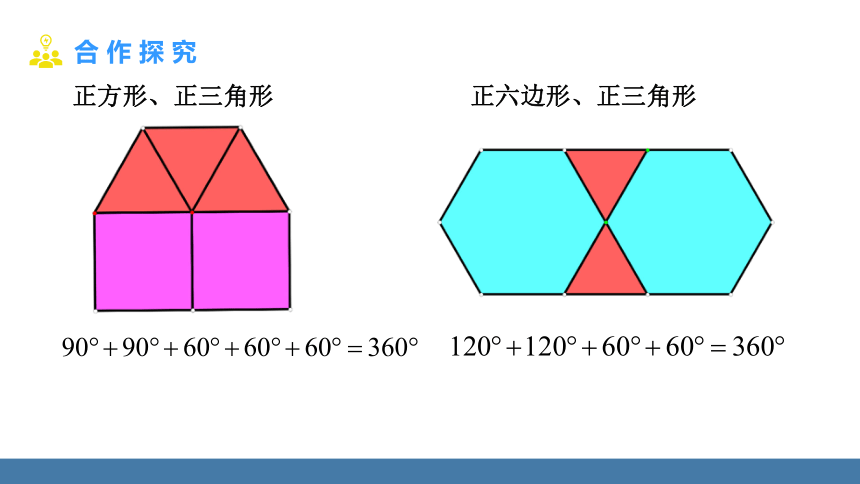
正三角形、正方形、正六边形
正多边形的每个内角都能被 360°整除.
知识点1 用两种正多边形铺设地面
问题 从正三角形、正方形、正五边形、正六边形、正八边形、正十边形、正十二边形……中任取两种进行组合是否能铺满地面呢?
正方形、正三角形
正六边形、正三角形
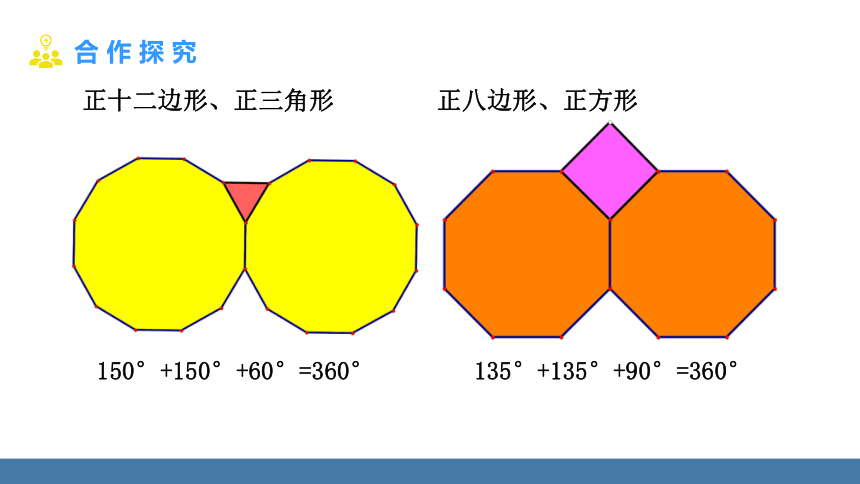
正十二边形、正三角形
150°+150°+60°=360°
正八边形、正方形
135°+135°+90°=360°
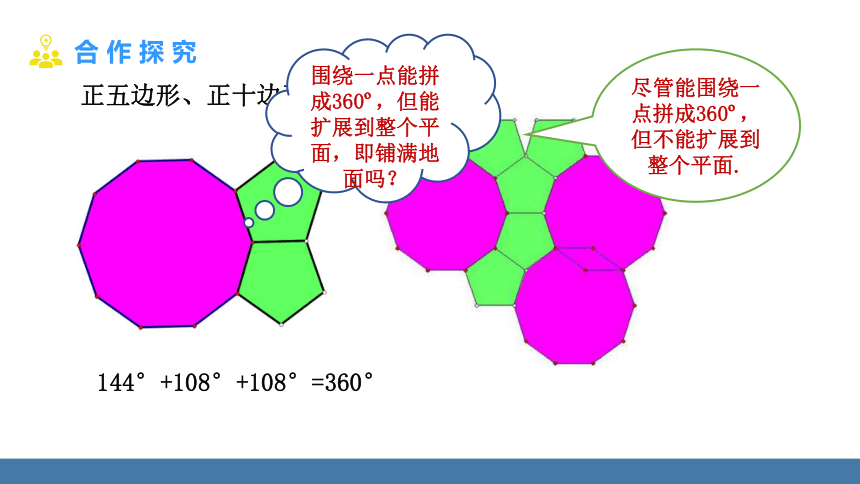
正五边形、正十边形
围绕一点能拼成360 ,但能扩展到整个平面,即铺满地面吗?
144°+108°+108°=360°
尽管能围绕一点拼成360 ,但不能扩展到整个平面.
知识点2 用两种以上正多边形铺设地面
问题 从正三角形、正方形、正五边形、正六边形、正八边形、正十边形、正十二边形……中任取几种进行组合是否能铺满地面呢?
正六边形、正方形、正三角形
120°+90°+90°+60°=360°
正十二边形、正方形、正六边形
150°+120°+90°=360°
正十二边形、正方形、正三角形
150°+90°+60°+60°=360°
多种正多边形应该满足什么样的条件才能铺满地面?
注:有时几种正多边形的组合能围绕一点拼成周角,但不能扩展到整个平面,即不能铺满平面.如:正五边形与正十边形的组合.
模型:
正多边形 1 的个数×正多边形 1 的内角度数 +
正多边形 2 的个数×正多边形 2 的内角度数 +… = 360
需满足围绕一点拼在一起的多种正多边形的内角之和为 360 .
例1 你能说说用正方形和正六边形不能镶嵌成一个平面图案的原因吗?
解:正方形的一个内角为 90°,正六边形的一个内角为 120°,
设若能进行平面镶嵌时正方形有x个,正六边形有y个,且x、y都是正整数,
则 90x + 120y = 360,
此时找不到同时满足x、y均为正整数的解,
故正方形和正六边形不能平面镶嵌.
方法总结 用任意几种正多边形铺满地面时,根据铺满地面的正多边形的种类,列出关于这几种正多边形的二元一次方程或三元一次方程,求其正整数解,方程有几组正整数解,就有几种铺设方法.没有整数解,则不能密铺.
1.现要选用两种不同的正多边形地砖铺地板,若选择了正四边形,
则可以再选择的正多边形是( )
A.正七边形 B.正五边形 C.正六边形 D.正八边形
2.用正三角形和正六边形铺成平面,共有不同的拼法是( )
A.1个 B.2个 C.3个 D.4个
D
B
3.在下列正多边形组合中,不能铺满地面的是( )
A.正八边形和正方形 B.正五边形和正八边形
C.正六边形和正三角形 D.正三角形和正方形
B
4.一幅美丽的图案,在某个顶点处由四个边长相等的正多边形铺满,其中的三个分别为正三角形、正方形、正六边形,那么另外一个为( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
5.利用边长相等的正三角形和正六边形的地砖镶嵌地面时,在每个顶点周围有 a 块正三角形和 b 块正六边形的地砖 (ab ≠ 0),则 a + b 的值为( )
A. 3 或 4 B. 4 或 5 C. 5 或 6 D. 4
B
B
围绕一点拼在一起的多种正多边形的内角之和为360°.
多种正多边形拼成平面条件
8.3 用正多边形铺设地面
2.用多种正多边形
掌握用多种正多边形拼成平面的规律及其运用.(重点)
1.在正三角形、正方形、正五边形、正六边形、正八边形中取一种,可以铺满地板的有哪些?
2.用同种正多边形瓷砖能不留空隙,不重叠地铺满地板的关键是什么?
正三角形、正方形、正六边形
正多边形的每个内角都能被 360°整除.
知识点1 用两种正多边形铺设地面
问题 从正三角形、正方形、正五边形、正六边形、正八边形、正十边形、正十二边形……中任取两种进行组合是否能铺满地面呢?
正方形、正三角形
正六边形、正三角形
正十二边形、正三角形
150°+150°+60°=360°
正八边形、正方形
135°+135°+90°=360°
正五边形、正十边形
围绕一点能拼成360 ,但能扩展到整个平面,即铺满地面吗?
144°+108°+108°=360°
尽管能围绕一点拼成360 ,但不能扩展到整个平面.
知识点2 用两种以上正多边形铺设地面
问题 从正三角形、正方形、正五边形、正六边形、正八边形、正十边形、正十二边形……中任取几种进行组合是否能铺满地面呢?
正六边形、正方形、正三角形
120°+90°+90°+60°=360°
正十二边形、正方形、正六边形
150°+120°+90°=360°
正十二边形、正方形、正三角形
150°+90°+60°+60°=360°
多种正多边形应该满足什么样的条件才能铺满地面?
注:有时几种正多边形的组合能围绕一点拼成周角,但不能扩展到整个平面,即不能铺满平面.如:正五边形与正十边形的组合.
模型:
正多边形 1 的个数×正多边形 1 的内角度数 +
正多边形 2 的个数×正多边形 2 的内角度数 +… = 360
需满足围绕一点拼在一起的多种正多边形的内角之和为 360 .
例1 你能说说用正方形和正六边形不能镶嵌成一个平面图案的原因吗?
解:正方形的一个内角为 90°,正六边形的一个内角为 120°,
设若能进行平面镶嵌时正方形有x个,正六边形有y个,且x、y都是正整数,
则 90x + 120y = 360,
此时找不到同时满足x、y均为正整数的解,
故正方形和正六边形不能平面镶嵌.
方法总结 用任意几种正多边形铺满地面时,根据铺满地面的正多边形的种类,列出关于这几种正多边形的二元一次方程或三元一次方程,求其正整数解,方程有几组正整数解,就有几种铺设方法.没有整数解,则不能密铺.
1.现要选用两种不同的正多边形地砖铺地板,若选择了正四边形,
则可以再选择的正多边形是( )
A.正七边形 B.正五边形 C.正六边形 D.正八边形
2.用正三角形和正六边形铺成平面,共有不同的拼法是( )
A.1个 B.2个 C.3个 D.4个
D
B
3.在下列正多边形组合中,不能铺满地面的是( )
A.正八边形和正方形 B.正五边形和正八边形
C.正六边形和正三角形 D.正三角形和正方形
B
4.一幅美丽的图案,在某个顶点处由四个边长相等的正多边形铺满,其中的三个分别为正三角形、正方形、正六边形,那么另外一个为( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
5.利用边长相等的正三角形和正六边形的地砖镶嵌地面时,在每个顶点周围有 a 块正三角形和 b 块正六边形的地砖 (ab ≠ 0),则 a + b 的值为( )
A. 3 或 4 B. 4 或 5 C. 5 或 6 D. 4
B
B
围绕一点拼在一起的多种正多边形的内角之和为360°.
多种正多边形拼成平面条件
