9.1.3 作轴对称图形 课件(共20张PPT)
文档属性
| 名称 | 9.1.3 作轴对称图形 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-17 07:10:00 | ||
图片预览





文档简介
(共20张PPT)
9.1.3 作轴对称图形
1. 能按要求作出简单平面图形关于直线对称的图形,探索作一般的轴对称图形的方法;(重点)
2. 探究较复杂的轴对称图形的作法.(难点)
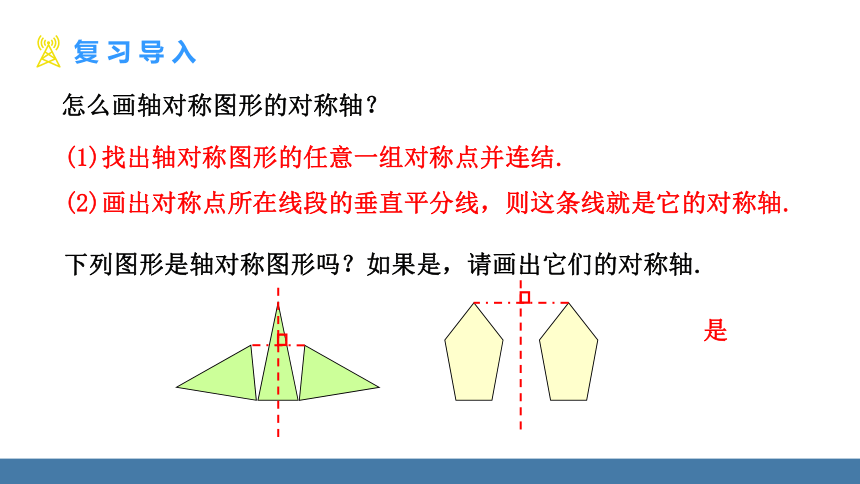
怎么画轴对称图形的对称轴?
(1)找出轴对称图形的任意一组对称点并连结.
(2)画出对称点所在线段的垂直平分线,则这条线就是它的对称轴.
下列图形是轴对称图形吗?如果是,请画出它们的对称轴.
是
我们本节课就来研究一下如何画轴对称图形.
将画好的轴对称图形遮掉左边一半或右边一半后,你能还原出原来的图形来吗?
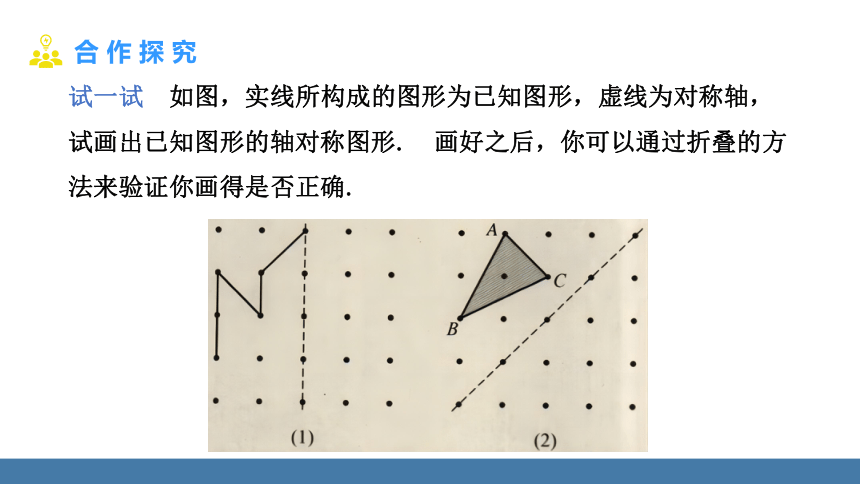
试一试 如图,实线所构成的图形为已知图形,虚线为对称轴,试画出已知图形的轴对称图形. 画好之后,你可以通过折叠的方法来验证你画得是否正确.
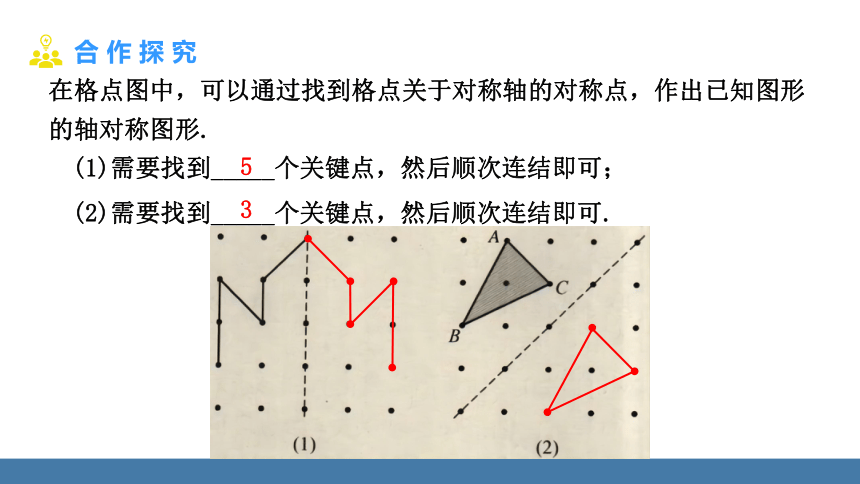
在格点图中,可以通过找到格点关于对称轴的对称点,作出已知图形的轴对称图形.
(1)需要找到_____个关键点,然后顺次连结即可;
(2)需要找到_____个关键点,然后顺次连结即可.
5
3
做一做 如果没有上述的格点图辅助,我们该如何做呢?如图,已知点 A 和直线l,试画出点 A 关于直线l 的对称点 A′.
﹒
l
A
﹒
A′
O
作法:
(1) 过点 A 作l的垂线,垂足为点 O;
(2) 在垂线上l的另一侧截取 OA′= OA.
则点 A′ 就是点 A 关于直线l 的对应点.
知识点1 画已知点的对称点
前面我们已经能利用尺规作图,作已知线段的垂直平分线,作已知角的平分线,那么如何利用尺规作图,过已知点作出已知直线的垂线?
已知点与已知直线可以有两种不同的位置关系:点在直线上;点在直线外.现分别按这两种情况作图.
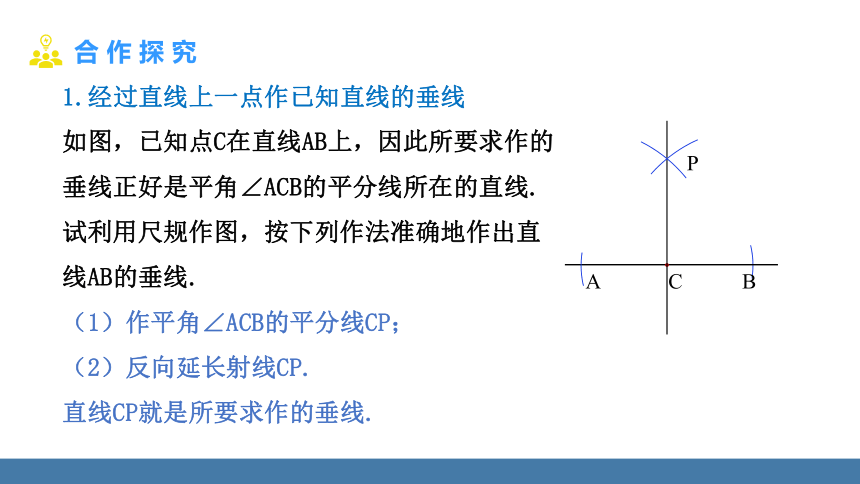
如图,已知点C在直线AB上,因此所要求作的垂线正好是平角∠ACB的平分线所在的直线.
试利用尺规作图,按下列作法准确地作出直线AB的垂线.
(1)作平角∠ACB的平分线CP;
(2)反向延长射线CP.
直线CP就是所要求作的垂线.
C
B
A
P
1.经过直线上一点作已知直线的垂线
如图,经过已知直线AB外一点C,试利用尺规作图,按下列作法准确地作出直线AB的垂线.
(1)以点C为圆心、适当长(大于点C到直线AB的距离)为半径作弧,交直线AB于M、N两点;
(2)分别以点M、N为圆心,相同长(大于线段MN长的一半)为半径作弧,两弧相交于点P;
(3)作直线CP.
直线CP就是所要求作的垂线.
C
B
A
M
N
P
2.经过直线外一点作已知直线的垂线
如图,点P在∠O的一边上,试过点P作该角两边的垂线.
A
O
P
B
如图,PA、PB即为所求作的垂线.
知识点2 画轴对称图形
例1 已知△ABC和直线l,作出△ABC关于直线l 对称的图形.
你能否从上面的画法中得到启示,帮助你解决例题?
分析:△ABC可以由三个顶点的位置确定,只要能分别画出这三个顶点关于直线l 的对应点,连结这些对应点,就能得到要作的图形.
A
B
C
作法:(1) 过点 A 作直线 l 的垂线,垂足为点 O,在垂线上截取 OA′ = OA,A′就是点 A 关于直线 l 的对应点;
(3) 连结 A′B′,B′C′,C′A′,得到△A′B′C′即为所求.
(2) 同理,分别画出点 B,C关于直线 l 的对应点 B′,C′;
A
B
C
A′
B′
C′
O
1.画轴对称图形的依据:
对称轴是对称点连线的垂直平分线,即一对对称点到对称轴的距离相等,所以只要过一个点向对称轴画垂线并截取相等的垂线段便可以得到它的对称点.
2.画轴对称图形的方法步骤:
(1)找出已知图形中的特殊点 (如线段的端点、角的顶点、折线的拐点等);
(2)作出特殊点关于对称轴的对称点;
(3)依次连结各对称点,得到的图形就是所要求作的图形.
1.下面是四位同学作△ABC关于直线MN的轴对称图形,其中正确的
是( )
B
2.下列说法中,正确的是( )
A.作一个图形的对称图形只能作一个
B.作一个图形的对称图形能作有限个
C.因为选取对称轴的位置不同,所以作一个图形的对称图形可有无数个
D.不规则的,复杂的图形不存在对称轴
C
3.如图,△ABC和△A′B′C′关于直线MN对称,其中点 A,A′是一组对称点,AA′交MN于点O,若AA′=8cm,则 A′O =____cm,∠A′OM =____度.
4
90
4.如图是由三个小正方形组成的图形,若在图中补画一个小正方形使补画后的图形为轴对称图形,则共有____种补法.
4
5. 在平面镜里看到其对面墙上电子钟示数如图所示,那么实际时间是_________.
5:01
6. 如图,作△ABC边BC上的高.
A
B
C
D
AD就是要求作的高.
1.画轴对称图形的依据:
对称轴是对称点连线的垂直平分线,即一对对称点到对称轴的距离相等,所以只要过一个点向对称轴画垂线并截取相等的垂线段便可以得到它的对称点.
2.画轴对称图形的方法步骤:
(1)找出已知图形中的特殊点 (如线段的端点、角的顶点、折线的拐点等);
(2)作出特殊点关于对称轴的对称点;
(3)依次连结各对称点,得到的图形就是所要求作的图形.
9.1.3 作轴对称图形
1. 能按要求作出简单平面图形关于直线对称的图形,探索作一般的轴对称图形的方法;(重点)
2. 探究较复杂的轴对称图形的作法.(难点)
怎么画轴对称图形的对称轴?
(1)找出轴对称图形的任意一组对称点并连结.
(2)画出对称点所在线段的垂直平分线,则这条线就是它的对称轴.
下列图形是轴对称图形吗?如果是,请画出它们的对称轴.
是
我们本节课就来研究一下如何画轴对称图形.
将画好的轴对称图形遮掉左边一半或右边一半后,你能还原出原来的图形来吗?
试一试 如图,实线所构成的图形为已知图形,虚线为对称轴,试画出已知图形的轴对称图形. 画好之后,你可以通过折叠的方法来验证你画得是否正确.
在格点图中,可以通过找到格点关于对称轴的对称点,作出已知图形的轴对称图形.
(1)需要找到_____个关键点,然后顺次连结即可;
(2)需要找到_____个关键点,然后顺次连结即可.
5
3
做一做 如果没有上述的格点图辅助,我们该如何做呢?如图,已知点 A 和直线l,试画出点 A 关于直线l 的对称点 A′.
﹒
l
A
﹒
A′
O
作法:
(1) 过点 A 作l的垂线,垂足为点 O;
(2) 在垂线上l的另一侧截取 OA′= OA.
则点 A′ 就是点 A 关于直线l 的对应点.
知识点1 画已知点的对称点
前面我们已经能利用尺规作图,作已知线段的垂直平分线,作已知角的平分线,那么如何利用尺规作图,过已知点作出已知直线的垂线?
已知点与已知直线可以有两种不同的位置关系:点在直线上;点在直线外.现分别按这两种情况作图.
如图,已知点C在直线AB上,因此所要求作的垂线正好是平角∠ACB的平分线所在的直线.
试利用尺规作图,按下列作法准确地作出直线AB的垂线.
(1)作平角∠ACB的平分线CP;
(2)反向延长射线CP.
直线CP就是所要求作的垂线.
C
B
A
P
1.经过直线上一点作已知直线的垂线
如图,经过已知直线AB外一点C,试利用尺规作图,按下列作法准确地作出直线AB的垂线.
(1)以点C为圆心、适当长(大于点C到直线AB的距离)为半径作弧,交直线AB于M、N两点;
(2)分别以点M、N为圆心,相同长(大于线段MN长的一半)为半径作弧,两弧相交于点P;
(3)作直线CP.
直线CP就是所要求作的垂线.
C
B
A
M
N
P
2.经过直线外一点作已知直线的垂线
如图,点P在∠O的一边上,试过点P作该角两边的垂线.
A
O
P
B
如图,PA、PB即为所求作的垂线.
知识点2 画轴对称图形
例1 已知△ABC和直线l,作出△ABC关于直线l 对称的图形.
你能否从上面的画法中得到启示,帮助你解决例题?
分析:△ABC可以由三个顶点的位置确定,只要能分别画出这三个顶点关于直线l 的对应点,连结这些对应点,就能得到要作的图形.
A
B
C
作法:(1) 过点 A 作直线 l 的垂线,垂足为点 O,在垂线上截取 OA′ = OA,A′就是点 A 关于直线 l 的对应点;
(3) 连结 A′B′,B′C′,C′A′,得到△A′B′C′即为所求.
(2) 同理,分别画出点 B,C关于直线 l 的对应点 B′,C′;
A
B
C
A′
B′
C′
O
1.画轴对称图形的依据:
对称轴是对称点连线的垂直平分线,即一对对称点到对称轴的距离相等,所以只要过一个点向对称轴画垂线并截取相等的垂线段便可以得到它的对称点.
2.画轴对称图形的方法步骤:
(1)找出已知图形中的特殊点 (如线段的端点、角的顶点、折线的拐点等);
(2)作出特殊点关于对称轴的对称点;
(3)依次连结各对称点,得到的图形就是所要求作的图形.
1.下面是四位同学作△ABC关于直线MN的轴对称图形,其中正确的
是( )
B
2.下列说法中,正确的是( )
A.作一个图形的对称图形只能作一个
B.作一个图形的对称图形能作有限个
C.因为选取对称轴的位置不同,所以作一个图形的对称图形可有无数个
D.不规则的,复杂的图形不存在对称轴
C
3.如图,△ABC和△A′B′C′关于直线MN对称,其中点 A,A′是一组对称点,AA′交MN于点O,若AA′=8cm,则 A′O =____cm,∠A′OM =____度.
4
90
4.如图是由三个小正方形组成的图形,若在图中补画一个小正方形使补画后的图形为轴对称图形,则共有____种补法.
4
5. 在平面镜里看到其对面墙上电子钟示数如图所示,那么实际时间是_________.
5:01
6. 如图,作△ABC边BC上的高.
A
B
C
D
AD就是要求作的高.
1.画轴对称图形的依据:
对称轴是对称点连线的垂直平分线,即一对对称点到对称轴的距离相等,所以只要过一个点向对称轴画垂线并截取相等的垂线段便可以得到它的对称点.
2.画轴对称图形的方法步骤:
(1)找出已知图形中的特殊点 (如线段的端点、角的顶点、折线的拐点等);
(2)作出特殊点关于对称轴的对称点;
(3)依次连结各对称点,得到的图形就是所要求作的图形.
