9.3.2 旋转的特征 课件(共19张PPT)
文档属性
| 名称 | 9.3.2 旋转的特征 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-17 07:11:11 | ||
图片预览



文档简介
(共19张PPT)
9.3.2 旋转的特征
1. 掌握旋转的特征;(重点)
2. 能用旋转的特征解决旋转作图的相关问题.(难点)
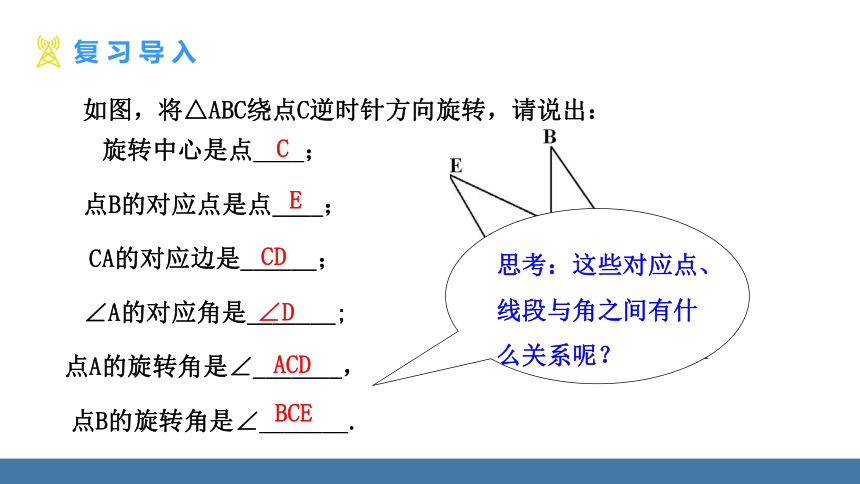
如图,将△ABC绕点C逆时针方向旋转,请说出:
旋转中心是点____;
点B的对应点是点____;
CA的对应边是______;
∠A的对应角是_______;
点A的旋转角是∠_______,
点B的旋转角是∠_______.
C
E
CD
∠D
ACD
BCE
思考:这些对应点、线段与角之间有什么关系呢?
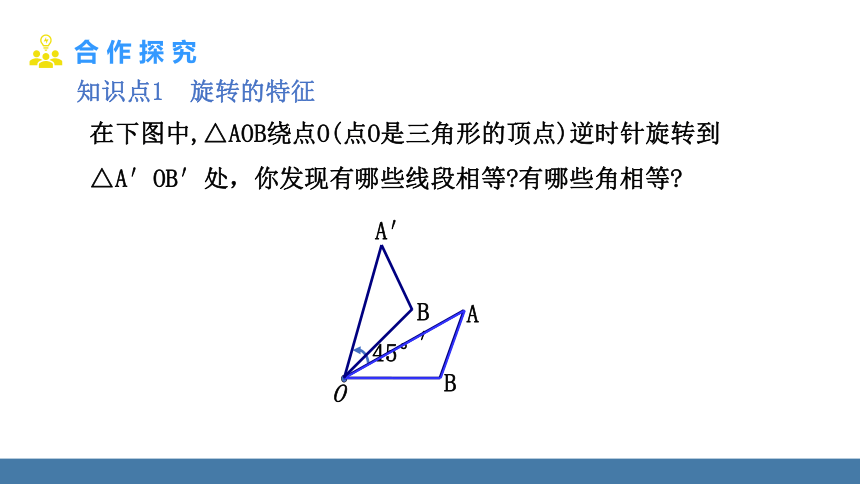
知识点1 旋转的特征
在下图中,△AOB绕点O(点O是三角形的顶点)逆时针旋转到△A′OB′处,你发现有哪些线段相等 有哪些角相等
45°
A′
B′
O
A
B
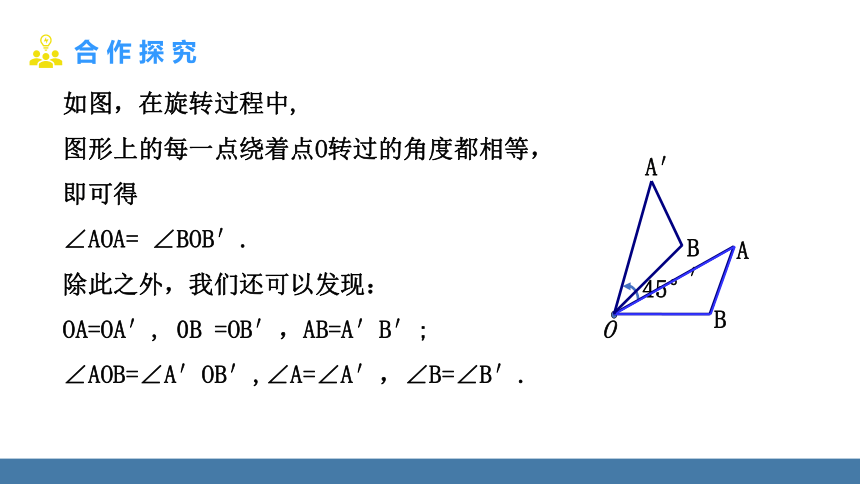
如图,在旋转过程中,
图形上的每一点绕着点O转过的角度都相等,即可得
∠AOA= ∠BOB′.
除此之外,我们还可以发现:
OA=OA′, 0B =OB′,AB=A′B′;
∠AOB=∠A′OB′,∠A=∠A′,∠B=∠B′.
45°
A′
B′
O
A
B
A′
B′
C′
O
60°
B
C
A
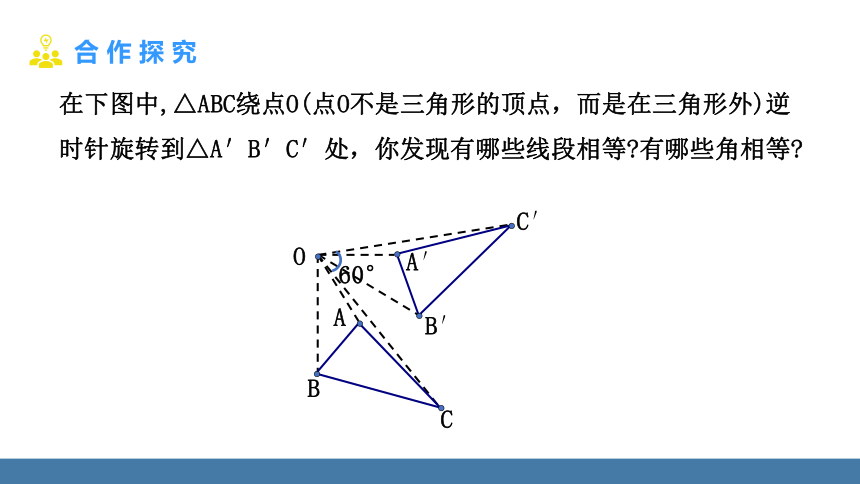
在下图中,△ABC绕点O(点O不是三角形的顶点,而是在三角形外)逆时针旋转到△A′B′C′处,你发现有哪些线段相等 有哪些角相等
A′
B′
C′
O
60°
B
C
A
如图,在旋转过程中,我们也可以发现类似的结果:
∠AOA′=∠BOB′=∠COC′;
OA=______,OB=______,OC=______;
AB=______,BC=______,CA=______;
∠CAB=__________,∠ABC=__________,
∠BCA=__________.
OA′
OB′
OC′
A′B′
B′C′
C′A′
∠C′A′B′
∠A′B′C′
∠B′C′A′
旋转的特征:
(1)图形中每一点都绕旋转中心按同一旋转方向旋转了同样大小的角度,都等于旋转角;
(2)对应点到旋转中心的距离相等;
(3)对应线段相等,对应角相等;
(4)旋转不改变图形的大小和形状.
2.如右图所示,将△ABC绕点A逆时针旋转60°得到△AB′C′,若AC⊥B′C′,则∠C的度数是 .
30°
1.如左图,点D是等边△ABC内一点, 若将△ABD旋转到△ACP, 则旋转中心是 ; 旋转角是 = 度,若连结DP,则△ADP是 三角形.
点A
∠BAC
60
等边
A
B
C
D
P
例1 如图所示,在8×8的正方形网格中有一个△ABC,画出以点B为旋转中心,将△ABC按顺时针方向旋转90°后的图形(画图不写画法).
解:如图所示,△A′BC′即为所求.
知识点2 旋转作图
归纳总结
旋转作图的方法:
(1)先确定图形的关键点;
(2)利用旋转的特征画出关键点的对应点;
(3)按原图形中的方式顺次连结对应点.
画图时一定要注意旋转中心、旋转方向和旋转角度.
1.如图所示,在由边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°,请画出旋转后得到的△AB′C′.
解:旋转后得到的△AB′C′如图所示.
2.如图所示,△ABC是等腰直角三角形,∠ACB=90°,画出将△ABC以点A为旋转中心,逆时针旋转45°后的图形.
解:如图所示,△AB′C′就是所画的图形.
做一做 如图,作△ABC和过点P的两条直线PQ、PR. 作出△ABC关于PQ对称的△A′B′C′,再画出△A′B′C′关于PR对称的△A″B″C″.
B
A
C
P
R
A′
B′
C′
A′′
B′′
C′′
观察△ABC和△△A″B″C″,你能发现这两个三角形有什么关系吗?
△A″B″C″可以看作是把△ABC绕点P旋转2倍∠QPR得到的.
Q
①相同:都是一种运动;运动前后不改变图形的形状和大小.
B
A
C
O
②不同
图形变换 运动方向 运动量的衡量
平移 直线 移动一定距离
旋转 顺时针或逆时针 转动一定的角度
平移和旋转的异同
1.一个图形经过平移或旋转,有以下的说法:①对应线段平行;②对应线段相等; ③对应角相等; ④图形的形状和大小都没有发生变化,其中正确的是( )
A、①②③ B、①②④ C、①③④ D、②③④
D
2.如图所示,在△ABC中,∠ACB=90°,∠A=30°,将△ABC绕点C逆时针旋转90°得到△DEC,则∠AED的度数为( )
A.105° B.120° C.135° D.150°
B
3.如图所示,在4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1.则它的旋转中心一定是( )
A.点A B.点B C.点C D.点D
B
4.如图所示,四边形ABCD是正方形,△ADE旋转后能与△ABF重合.旋转中心是哪一点 顺时针旋转了多少度
解:旋转中心是点A,顺时针旋转了90°.
5.如图所示,请画出将△ABC绕点D按顺时针方向旋转90°后的图形.
解:如图所示,△A′B′C′就是所画的三角形.
旋转的特征
对应线段相等,对应角相等
对应点到旋转中心的距离相等
旋转角都相等
9.3.2 旋转的特征
1. 掌握旋转的特征;(重点)
2. 能用旋转的特征解决旋转作图的相关问题.(难点)
如图,将△ABC绕点C逆时针方向旋转,请说出:
旋转中心是点____;
点B的对应点是点____;
CA的对应边是______;
∠A的对应角是_______;
点A的旋转角是∠_______,
点B的旋转角是∠_______.
C
E
CD
∠D
ACD
BCE
思考:这些对应点、线段与角之间有什么关系呢?
知识点1 旋转的特征
在下图中,△AOB绕点O(点O是三角形的顶点)逆时针旋转到△A′OB′处,你发现有哪些线段相等 有哪些角相等
45°
A′
B′
O
A
B
如图,在旋转过程中,
图形上的每一点绕着点O转过的角度都相等,即可得
∠AOA= ∠BOB′.
除此之外,我们还可以发现:
OA=OA′, 0B =OB′,AB=A′B′;
∠AOB=∠A′OB′,∠A=∠A′,∠B=∠B′.
45°
A′
B′
O
A
B
A′
B′
C′
O
60°
B
C
A
在下图中,△ABC绕点O(点O不是三角形的顶点,而是在三角形外)逆时针旋转到△A′B′C′处,你发现有哪些线段相等 有哪些角相等
A′
B′
C′
O
60°
B
C
A
如图,在旋转过程中,我们也可以发现类似的结果:
∠AOA′=∠BOB′=∠COC′;
OA=______,OB=______,OC=______;
AB=______,BC=______,CA=______;
∠CAB=__________,∠ABC=__________,
∠BCA=__________.
OA′
OB′
OC′
A′B′
B′C′
C′A′
∠C′A′B′
∠A′B′C′
∠B′C′A′
旋转的特征:
(1)图形中每一点都绕旋转中心按同一旋转方向旋转了同样大小的角度,都等于旋转角;
(2)对应点到旋转中心的距离相等;
(3)对应线段相等,对应角相等;
(4)旋转不改变图形的大小和形状.
2.如右图所示,将△ABC绕点A逆时针旋转60°得到△AB′C′,若AC⊥B′C′,则∠C的度数是 .
30°
1.如左图,点D是等边△ABC内一点, 若将△ABD旋转到△ACP, 则旋转中心是 ; 旋转角是 = 度,若连结DP,则△ADP是 三角形.
点A
∠BAC
60
等边
A
B
C
D
P
例1 如图所示,在8×8的正方形网格中有一个△ABC,画出以点B为旋转中心,将△ABC按顺时针方向旋转90°后的图形(画图不写画法).
解:如图所示,△A′BC′即为所求.
知识点2 旋转作图
归纳总结
旋转作图的方法:
(1)先确定图形的关键点;
(2)利用旋转的特征画出关键点的对应点;
(3)按原图形中的方式顺次连结对应点.
画图时一定要注意旋转中心、旋转方向和旋转角度.
1.如图所示,在由边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°,请画出旋转后得到的△AB′C′.
解:旋转后得到的△AB′C′如图所示.
2.如图所示,△ABC是等腰直角三角形,∠ACB=90°,画出将△ABC以点A为旋转中心,逆时针旋转45°后的图形.
解:如图所示,△AB′C′就是所画的图形.
做一做 如图,作△ABC和过点P的两条直线PQ、PR. 作出△ABC关于PQ对称的△A′B′C′,再画出△A′B′C′关于PR对称的△A″B″C″.
B
A
C
P
R
A′
B′
C′
A′′
B′′
C′′
观察△ABC和△△A″B″C″,你能发现这两个三角形有什么关系吗?
△A″B″C″可以看作是把△ABC绕点P旋转2倍∠QPR得到的.
Q
①相同:都是一种运动;运动前后不改变图形的形状和大小.
B
A
C
O
②不同
图形变换 运动方向 运动量的衡量
平移 直线 移动一定距离
旋转 顺时针或逆时针 转动一定的角度
平移和旋转的异同
1.一个图形经过平移或旋转,有以下的说法:①对应线段平行;②对应线段相等; ③对应角相等; ④图形的形状和大小都没有发生变化,其中正确的是( )
A、①②③ B、①②④ C、①③④ D、②③④
D
2.如图所示,在△ABC中,∠ACB=90°,∠A=30°,将△ABC绕点C逆时针旋转90°得到△DEC,则∠AED的度数为( )
A.105° B.120° C.135° D.150°
B
3.如图所示,在4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1.则它的旋转中心一定是( )
A.点A B.点B C.点C D.点D
B
4.如图所示,四边形ABCD是正方形,△ADE旋转后能与△ABF重合.旋转中心是哪一点 顺时针旋转了多少度
解:旋转中心是点A,顺时针旋转了90°.
5.如图所示,请画出将△ABC绕点D按顺时针方向旋转90°后的图形.
解:如图所示,△A′B′C′就是所画的三角形.
旋转的特征
对应线段相等,对应角相等
对应点到旋转中心的距离相等
旋转角都相等
