9.2.2 平移的特征 课件(共15张PPT)
文档属性
| 名称 | 9.2.2 平移的特征 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-17 08:49:19 | ||
图片预览




文档简介
(共15张PPT)
9.2.2 平移的特征
1.理解平移的特征.(重点)
2.能根据所给条件作简单的平面图形平移后的图形.(难点)
如图,在画平行线的时候,有时为了需要,将直尺与三角尺放在倾斜的位置上.
动手做做:
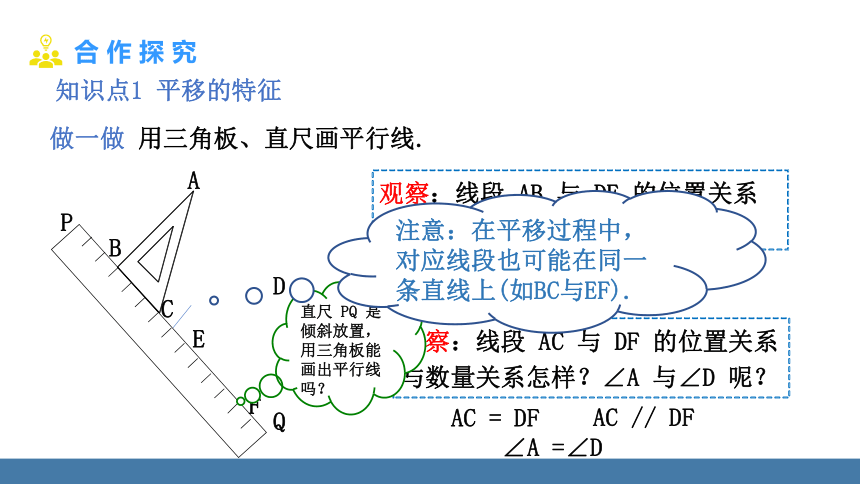
做一做 用三角板、直尺画平行线.
P
Q
D
E
F
A
观察:线段 AB 与 DE 的位置关系与数量关系怎样?∠B 与∠E 呢?
AB // DE
AB = DE
∠B =∠E
观察:线段 AC 与 DF 的位置关系与数量关系怎样?∠A 与∠D 呢?
AC // DF
AC = DF
∠A =∠D
B
C
F
直尺 PQ 是倾斜放置,用三角板能画出平行线吗?
注意:在平移过程中,对应线段也可能在同一条直线上(如BC与EF).
知识点1 平移的特征
归纳 平移的特征:
平移后的图形与原来图形的对应线段平行 (或在同一条直线上)且相等,对应角相等,图形的形状和大小不变.
注意:
(1)连结对应点的线段的长度就是平移距离(上述中的BE);
(2)从原图上一点到其对应点的方向即起始点到终止点的方向为平移方向;
(3)平移前后图形的对应边平行且相等,对应角相等.
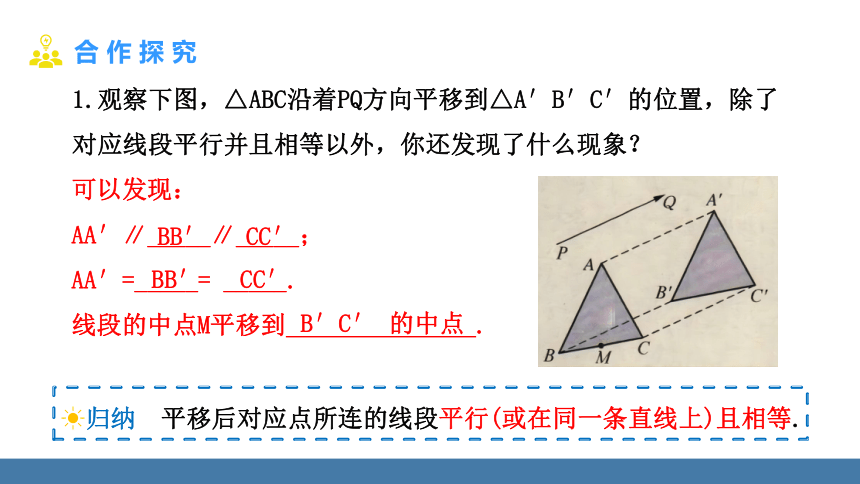
1.观察下图,△ABC沿着PQ方向平移到△A′B′C′的位置,除了对应线段平行并且相等以外,你还发现了什么现象?
可以发现:
AA′∥_____∥_____;
AA′=_____= _____.
线段的中点M平移到 .
BB′
CC′
BB′
CC′
B′C′ 的中点
归纳 平移后对应点所连的线段平行(或在同一条直线上)且相等.
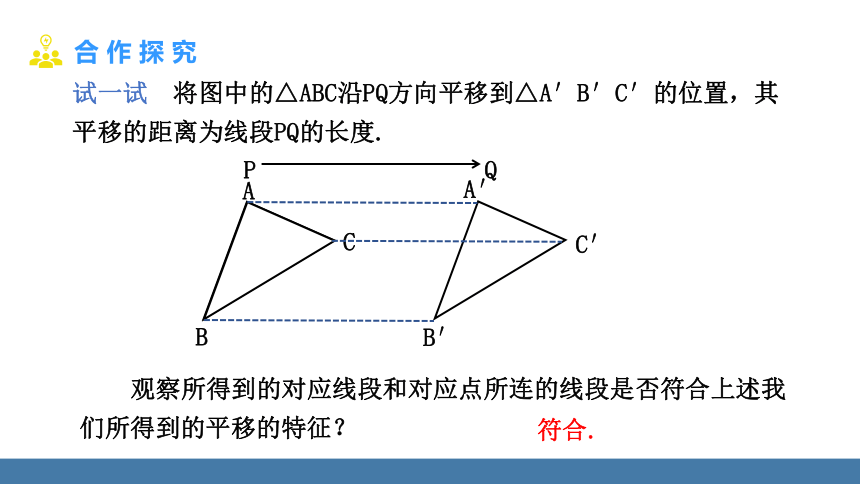
试一试 将图中的△ABC沿PQ方向平移到△A′B′C′的位置,其平移的距离为线段PQ的长度.
P Q
A
B
C
A′
B′
C′
观察所得到的对应线段和对应点所连的线段是否符合上述我们所得到的平移的特征?
符合.
例 如图,将△ABC平移到△A′B′C′的位置.指出平移的方向,并量出平移的距离.(精确到1mm)
解:由于点A与点A′是一对对应点,因此,如图,连结AA′,平移的方向就是点A到点A′的方向,平移的距离就是线段AA′的长,经测量可知,约25mm.
知识点2 平移作图
试一试 在如图的方格纸中,作出将图中的△ABC向右平移4格后的△A′B′C′,然后再作出将△A′B′C′向上平移3格后的△A″B″C″.
A
B
C
A′
B′
C′
A′′
B′′
C′′
△A″B″C″是否可以看成是△ABC经过一次平移而得到的?如果是,那么平移的方向和距离分别是什么?
A
B
C
A′
B′
C′
A′′
B′′
C′′
可以看成是△ABC经过一次平移而得到的,平移方向是沿点C到点C″或点A到点A″或点B到点B″的方向,平移距离是线段CC″或线段AA″或线段BB″的长度.
1.如图在一块长为12m,宽为6m的长方形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是2m)则空白部分表示的草地面积是( )
A. 70 B. 60
C. 48 D. 18
B
2.如图,将△ABC沿BC方向平移2cm得到△DEF,若△ABC的周长为16cm,则四边形ABFD的周长为( )
A. 16 cm B. 18 cm
C. 20 cm D. 22 cm
C
3.如左图,AD是△ABC的中线,将△ABC沿射线BC方向平移2cm得到△EDF,则DC的长为_____ cm.
2
4.如右图,根据图中的数据,计算阴影部分的面积为 _____.
104
5.如图所示,平移四边形ABCD,使点A移动到点A′,画出平移后的四边形A′B′C′D′,并指出平移的方向和平移的距离.
解:(1)连接AA′;
(2)过点B、C、D分别作AA′的平行线l1、l2、l3;
(3)在l1上截取BB′= AA′,在l2,l3上按同样的方法截取CC′=AA′,DD′= AA′;
(4)连结A′B′、B′C′、C′D′、D′A′得到的四边形A′B′C′D′即为所求的四边形,如图所示.
平移的方向为射线AA′的方向,平移的距离为线段AA′的长.
平移的特征
1.平移后的图形与原来图形的对应线段平行 (或在同一条直线上)且相等,对应角相等,图形的形状与大小不变.
2.平移后对应点所连的线段平行且相等.
9.2.2 平移的特征
1.理解平移的特征.(重点)
2.能根据所给条件作简单的平面图形平移后的图形.(难点)
如图,在画平行线的时候,有时为了需要,将直尺与三角尺放在倾斜的位置上.
动手做做:
做一做 用三角板、直尺画平行线.
P
Q
D
E
F
A
观察:线段 AB 与 DE 的位置关系与数量关系怎样?∠B 与∠E 呢?
AB // DE
AB = DE
∠B =∠E
观察:线段 AC 与 DF 的位置关系与数量关系怎样?∠A 与∠D 呢?
AC // DF
AC = DF
∠A =∠D
B
C
F
直尺 PQ 是倾斜放置,用三角板能画出平行线吗?
注意:在平移过程中,对应线段也可能在同一条直线上(如BC与EF).
知识点1 平移的特征
归纳 平移的特征:
平移后的图形与原来图形的对应线段平行 (或在同一条直线上)且相等,对应角相等,图形的形状和大小不变.
注意:
(1)连结对应点的线段的长度就是平移距离(上述中的BE);
(2)从原图上一点到其对应点的方向即起始点到终止点的方向为平移方向;
(3)平移前后图形的对应边平行且相等,对应角相等.
1.观察下图,△ABC沿着PQ方向平移到△A′B′C′的位置,除了对应线段平行并且相等以外,你还发现了什么现象?
可以发现:
AA′∥_____∥_____;
AA′=_____= _____.
线段的中点M平移到 .
BB′
CC′
BB′
CC′
B′C′ 的中点
归纳 平移后对应点所连的线段平行(或在同一条直线上)且相等.
试一试 将图中的△ABC沿PQ方向平移到△A′B′C′的位置,其平移的距离为线段PQ的长度.
P Q
A
B
C
A′
B′
C′
观察所得到的对应线段和对应点所连的线段是否符合上述我们所得到的平移的特征?
符合.
例 如图,将△ABC平移到△A′B′C′的位置.指出平移的方向,并量出平移的距离.(精确到1mm)
解:由于点A与点A′是一对对应点,因此,如图,连结AA′,平移的方向就是点A到点A′的方向,平移的距离就是线段AA′的长,经测量可知,约25mm.
知识点2 平移作图
试一试 在如图的方格纸中,作出将图中的△ABC向右平移4格后的△A′B′C′,然后再作出将△A′B′C′向上平移3格后的△A″B″C″.
A
B
C
A′
B′
C′
A′′
B′′
C′′
△A″B″C″是否可以看成是△ABC经过一次平移而得到的?如果是,那么平移的方向和距离分别是什么?
A
B
C
A′
B′
C′
A′′
B′′
C′′
可以看成是△ABC经过一次平移而得到的,平移方向是沿点C到点C″或点A到点A″或点B到点B″的方向,平移距离是线段CC″或线段AA″或线段BB″的长度.
1.如图在一块长为12m,宽为6m的长方形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是2m)则空白部分表示的草地面积是( )
A. 70 B. 60
C. 48 D. 18
B
2.如图,将△ABC沿BC方向平移2cm得到△DEF,若△ABC的周长为16cm,则四边形ABFD的周长为( )
A. 16 cm B. 18 cm
C. 20 cm D. 22 cm
C
3.如左图,AD是△ABC的中线,将△ABC沿射线BC方向平移2cm得到△EDF,则DC的长为_____ cm.
2
4.如右图,根据图中的数据,计算阴影部分的面积为 _____.
104
5.如图所示,平移四边形ABCD,使点A移动到点A′,画出平移后的四边形A′B′C′D′,并指出平移的方向和平移的距离.
解:(1)连接AA′;
(2)过点B、C、D分别作AA′的平行线l1、l2、l3;
(3)在l1上截取BB′= AA′,在l2,l3上按同样的方法截取CC′=AA′,DD′= AA′;
(4)连结A′B′、B′C′、C′D′、D′A′得到的四边形A′B′C′D′即为所求的四边形,如图所示.
平移的方向为射线AA′的方向,平移的距离为线段AA′的长.
平移的特征
1.平移后的图形与原来图形的对应线段平行 (或在同一条直线上)且相等,对应角相等,图形的形状与大小不变.
2.平移后对应点所连的线段平行且相等.
