9.5 图形的全等 课件(共22张PPT)
文档属性
| 名称 | 9.5 图形的全等 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-17 00:00:00 | ||
图片预览




文档简介
(共22张PPT)
9.5 图形的全等
1.理解全等图形的定义.
2.探究全等图形的性质与判定.(难点)
3.从全等图形的判定到全等三角形的判定.(重点)
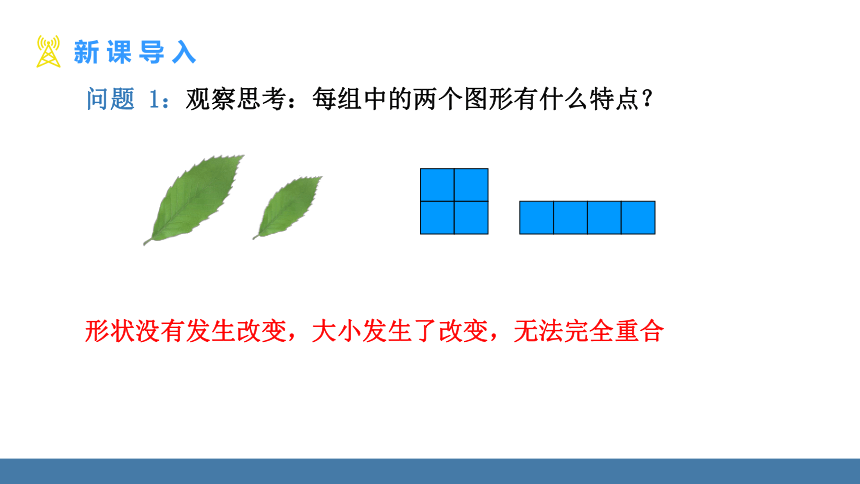
问题 1:观察思考:每组中的两个图形有什么特点?
形状没有发生改变,大小发生了改变,无法完全重合
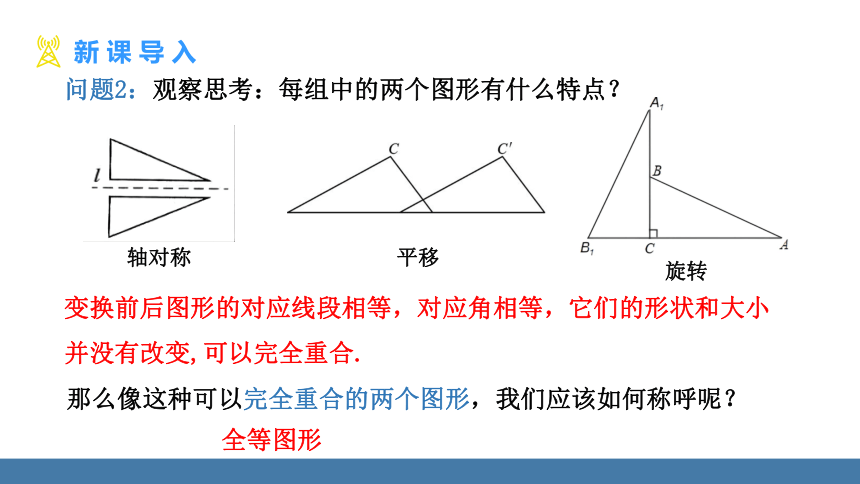
问题2:观察思考:每组中的两个图形有什么特点?
轴对称
平移
旋转
变换前后图形的对应线段相等,对应角相等,它们的形状和大小并没有改变,可以完全重合.
那么像这种可以完全重合的两个图形,我们应该如何称呼呢?
全等图形
回到问题1中,下列两组图形是不是全等图形,为什么?
两个图形形状相同,但大小不同
两个图形面积相同,但形状不同
它们不能重合,不是全等图形
注意:全等图形的特征是完全重合.
知识点1 全等图形
我们知道,同一底片冲洗出来的相同尺寸的两张照片是全等的,不同尺寸的两张是不全等的.
如图:已知△ABC.
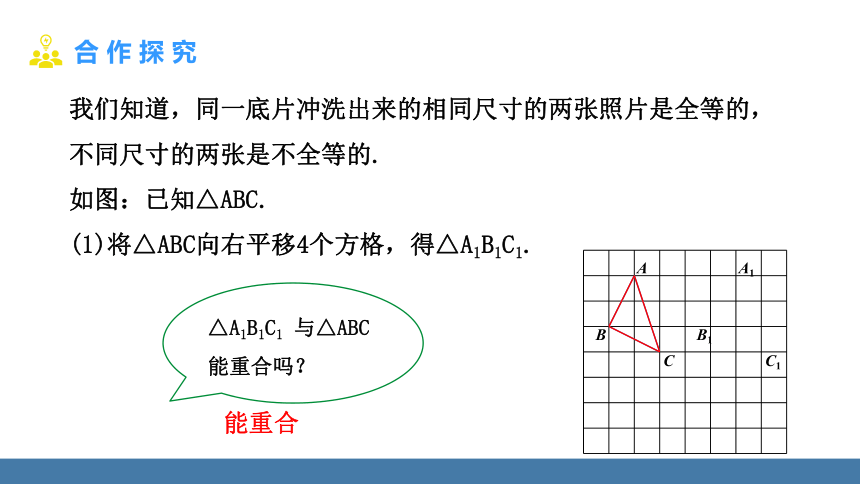
(1)将△ABC向右平移4个方格,得△A1B1C1.
A
B
C
A1
B1
C1
能重合
△A1B1C1 与△ABC 能重合吗?
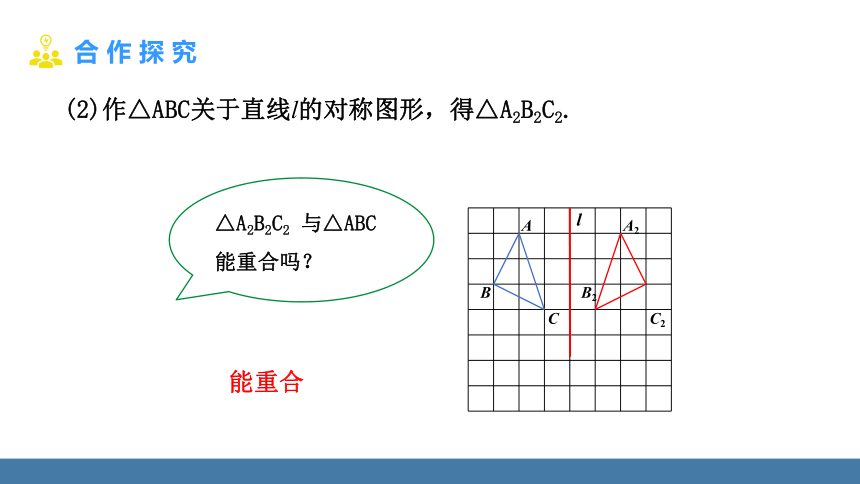
(2)作△ABC关于直线l的对称图形,得△A2B2C2.
A
B
C
A2
B2
C2
l
能重合
△A2B2C2 与△ABC 能重合吗?
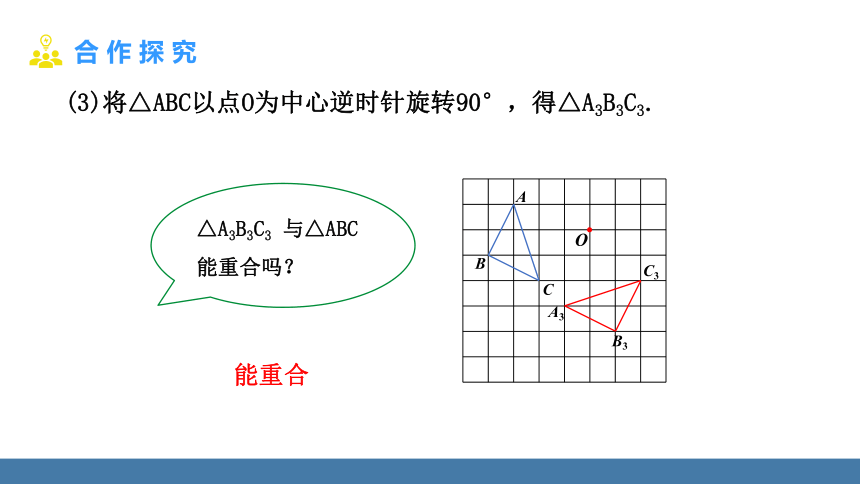
(3)将△ABC以点O为中心逆时针旋转90°,得△A3B3C3.
A
B
C
A3
B3
C3
O
能重合
△A3B3C3 与△ABC 能重合吗?
归纳
1.两个能够完全重合的图形称为全等图形.
2.图形经过轴对称、平移或旋转等变换所得到的新图形一定与原图形全等.
3.两个全等图形经过轴对称、平移或旋转等变换后一定能够互相重合.
例1 下列叙述中错误的是( )
A. 能够重合的图形称为全等图形
B. 全等图形的形状和大小都相同
C. 所有正方形都是全等图形
D. 形状和大小都相同的两个图形是全等图形
C
观察图中的两对多边形,每对中的其中一个可以经过怎样的变换和另一个图形重合?
知识点2 全等多边形的性质和判定
归纳 两对多边形都是全等图形,也称为全等多边形. 两个全等的多边形,经过变换而重合,相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角.
如下图中的两个五边形是全等的,记作五边形ABCDE≌五边形 A′B′C′D′E′(这里,符号“≌”表示全等,读作“全等于”).
点A与点A′、点B与点B′、点C与点C′、点D与点D′、点E与点E′分别是对应顶点.
归纳
全等多边形的性质:
全等多边形的对应边相等,对应角相等.
全等多边形的判定方法:
边、角分别对应相等的两个多边形称为全等多边形.
全等三角形的性质:
全等三角形的对应边、对应角分别相等.
全等三角形的判定方法:
如果两个三角形的边、角分别对应相等,那么这两个三角形全等.
知识点3 全等三角形的性质
如图所示,△ABC≌△DEF,且∠A=∠D,∠B=∠E.你能指出它们之间其他的对应顶点、对应角和对应边吗?
解:对应顶点:_____________________________________;
对应边:________________________________;
对应角:________________________________.
点A 与点D、
点B 与点E、
点C 与点F
AB与DE、
BC与EF、
CA与ED
∠A与∠D、
∠B与∠E、
∠C与∠F
例2 如图,△ABC沿着BC的方向平移至△DEF,∠A=80°,∠B=60°,求∠F的度数.
解:由图形平移的特征,可知△ABC与△DEF的形状与大小相同,即△ABC≌△DEF.
∴∠D=∠A= 80°(全等三角形的对应角相等).
同理∠DEF=∠B=60°.
又∵∠D+∠DEF+∠F= 180°(三角形的内角和等于180°),
∴∠F=180°-∠D-∠DEF
=180°- 80°- 60°= 40°
1.下列说法正确的是( )
①用一张像纸冲洗出来的10张1寸像片是全等图形;
②我国国旗上的4颗小五角星是全等图形;
③所有的正方形是全等图形;
④全等图形的面积一定相等.
A.1个 B.2个 C.3个 D.4个
C
2.如图,已知△ABC和△DCB全等,AB和DC是对应边,BC是公共边,说出这两个全等三角形的其他对应边和对应角以及对应顶点.
B
D
A
C
对应边:AC对应DB,BC对应CB
对应角:∠A对应∠D,∠ABC对应∠DCB,∠ACB对应∠DBC
对应顶点:A对应D,C对应B,B对应C
3.已知△ABC≌△DEF,△ABC的周长是40cm,AB=10cm,BC=16cm,求DF的长度.
解:∵ △ABC ≌ △DEF(已知)
∴AC = DF(全等三角形的对应边等) ∵△ABC 的周长是 40cm,
AB=10cm,BC=16cm, (已知)
∴ AC =40-10-16 = 14(cm),
∴ DF=14cm.
A
B
C
D
E
F
4.如图,△ABC绕顶点A逆时针旋转30°至△ADE,∠B=40°,∠DAC=50°.求∠E的度数.
A
B
C
D
E
解:∵△ABC绕顶点A逆时针旋转30°至△ADE,
∴△ABC ≌ △ADE,∠BAD = 30°,∠C =∠E.
∵∠DAC = 50°,
∴∠BAC =∠BAD +∠DAC = 80°.
又∵∠B = 40°,
∴∠C = 180°-∠B -∠BAC =60°.
∴∠E = 60°.
定义
全等图形
能够完全重合的两个图形
对应角相等,对应边相等
性质
全等三角形
性质:对应边、角分别相等.
判定方法:边、角分别对应相等,则三角形全等.
9.5 图形的全等
1.理解全等图形的定义.
2.探究全等图形的性质与判定.(难点)
3.从全等图形的判定到全等三角形的判定.(重点)
问题 1:观察思考:每组中的两个图形有什么特点?
形状没有发生改变,大小发生了改变,无法完全重合
问题2:观察思考:每组中的两个图形有什么特点?
轴对称
平移
旋转
变换前后图形的对应线段相等,对应角相等,它们的形状和大小并没有改变,可以完全重合.
那么像这种可以完全重合的两个图形,我们应该如何称呼呢?
全等图形
回到问题1中,下列两组图形是不是全等图形,为什么?
两个图形形状相同,但大小不同
两个图形面积相同,但形状不同
它们不能重合,不是全等图形
注意:全等图形的特征是完全重合.
知识点1 全等图形
我们知道,同一底片冲洗出来的相同尺寸的两张照片是全等的,不同尺寸的两张是不全等的.
如图:已知△ABC.
(1)将△ABC向右平移4个方格,得△A1B1C1.
A
B
C
A1
B1
C1
能重合
△A1B1C1 与△ABC 能重合吗?
(2)作△ABC关于直线l的对称图形,得△A2B2C2.
A
B
C
A2
B2
C2
l
能重合
△A2B2C2 与△ABC 能重合吗?
(3)将△ABC以点O为中心逆时针旋转90°,得△A3B3C3.
A
B
C
A3
B3
C3
O
能重合
△A3B3C3 与△ABC 能重合吗?
归纳
1.两个能够完全重合的图形称为全等图形.
2.图形经过轴对称、平移或旋转等变换所得到的新图形一定与原图形全等.
3.两个全等图形经过轴对称、平移或旋转等变换后一定能够互相重合.
例1 下列叙述中错误的是( )
A. 能够重合的图形称为全等图形
B. 全等图形的形状和大小都相同
C. 所有正方形都是全等图形
D. 形状和大小都相同的两个图形是全等图形
C
观察图中的两对多边形,每对中的其中一个可以经过怎样的变换和另一个图形重合?
知识点2 全等多边形的性质和判定
归纳 两对多边形都是全等图形,也称为全等多边形. 两个全等的多边形,经过变换而重合,相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角.
如下图中的两个五边形是全等的,记作五边形ABCDE≌五边形 A′B′C′D′E′(这里,符号“≌”表示全等,读作“全等于”).
点A与点A′、点B与点B′、点C与点C′、点D与点D′、点E与点E′分别是对应顶点.
归纳
全等多边形的性质:
全等多边形的对应边相等,对应角相等.
全等多边形的判定方法:
边、角分别对应相等的两个多边形称为全等多边形.
全等三角形的性质:
全等三角形的对应边、对应角分别相等.
全等三角形的判定方法:
如果两个三角形的边、角分别对应相等,那么这两个三角形全等.
知识点3 全等三角形的性质
如图所示,△ABC≌△DEF,且∠A=∠D,∠B=∠E.你能指出它们之间其他的对应顶点、对应角和对应边吗?
解:对应顶点:_____________________________________;
对应边:________________________________;
对应角:________________________________.
点A 与点D、
点B 与点E、
点C 与点F
AB与DE、
BC与EF、
CA与ED
∠A与∠D、
∠B与∠E、
∠C与∠F
例2 如图,△ABC沿着BC的方向平移至△DEF,∠A=80°,∠B=60°,求∠F的度数.
解:由图形平移的特征,可知△ABC与△DEF的形状与大小相同,即△ABC≌△DEF.
∴∠D=∠A= 80°(全等三角形的对应角相等).
同理∠DEF=∠B=60°.
又∵∠D+∠DEF+∠F= 180°(三角形的内角和等于180°),
∴∠F=180°-∠D-∠DEF
=180°- 80°- 60°= 40°
1.下列说法正确的是( )
①用一张像纸冲洗出来的10张1寸像片是全等图形;
②我国国旗上的4颗小五角星是全等图形;
③所有的正方形是全等图形;
④全等图形的面积一定相等.
A.1个 B.2个 C.3个 D.4个
C
2.如图,已知△ABC和△DCB全等,AB和DC是对应边,BC是公共边,说出这两个全等三角形的其他对应边和对应角以及对应顶点.
B
D
A
C
对应边:AC对应DB,BC对应CB
对应角:∠A对应∠D,∠ABC对应∠DCB,∠ACB对应∠DBC
对应顶点:A对应D,C对应B,B对应C
3.已知△ABC≌△DEF,△ABC的周长是40cm,AB=10cm,BC=16cm,求DF的长度.
解:∵ △ABC ≌ △DEF(已知)
∴AC = DF(全等三角形的对应边等) ∵△ABC 的周长是 40cm,
AB=10cm,BC=16cm, (已知)
∴ AC =40-10-16 = 14(cm),
∴ DF=14cm.
A
B
C
D
E
F
4.如图,△ABC绕顶点A逆时针旋转30°至△ADE,∠B=40°,∠DAC=50°.求∠E的度数.
A
B
C
D
E
解:∵△ABC绕顶点A逆时针旋转30°至△ADE,
∴△ABC ≌ △ADE,∠BAD = 30°,∠C =∠E.
∵∠DAC = 50°,
∴∠BAC =∠BAD +∠DAC = 80°.
又∵∠B = 40°,
∴∠C = 180°-∠B -∠BAC =60°.
∴∠E = 60°.
定义
全等图形
能够完全重合的两个图形
对应角相等,对应边相等
性质
全等三角形
性质:对应边、角分别相等.
判定方法:边、角分别对应相等,则三角形全等.
