人教版数学八年级上册数学几何九大模型(含答案)
文档属性
| 名称 | 人教版数学八年级上册数学几何九大模型(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-16 19:07:24 | ||
图片预览

文档简介
人教数学八年级上册数学几何模型
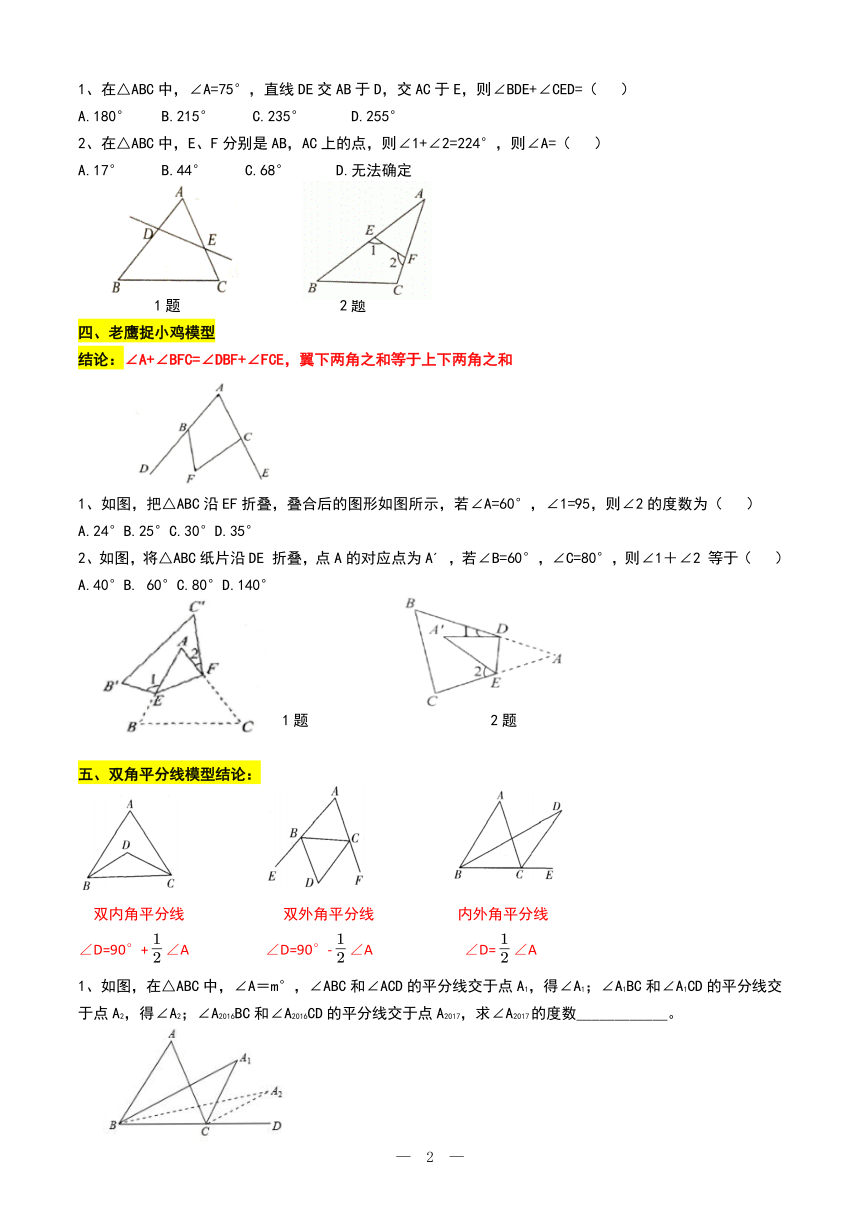
一、8字模型
结论:①∠A+∠B=∠C+∠D;②AB+CD<AD+BC
斜8字型(蝴蝶型) 燕尾型
1、如图,已知D是△ABC的BC边的延长线上一点,DF⊥AB,交AB于点F,交AC于点E,∠A=56°,∠D=30°,则∠ACB的度数为_________
2、如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为_________
3、求:∠CAD+∠B+∠C+∠D+∠E=_________
1题 2题 3题
燕尾(飞镖)模型
结论:∠BDC=∠A+∠B+∠C
1、将一副直角三角板如图放置,使两直角边重合,则∠1的度数为__________
2、如图,是一块不规则的纸片,∠ABC=∠DEF=80°,则∠A+∠C+∠D+∠F的度数为__________
3、如图,求∠A+∠B+∠C+∠D+∠E+∠F= .
1题 2题 3题
A字模型
结论:∠DBC+∠ECB=180°+∠A
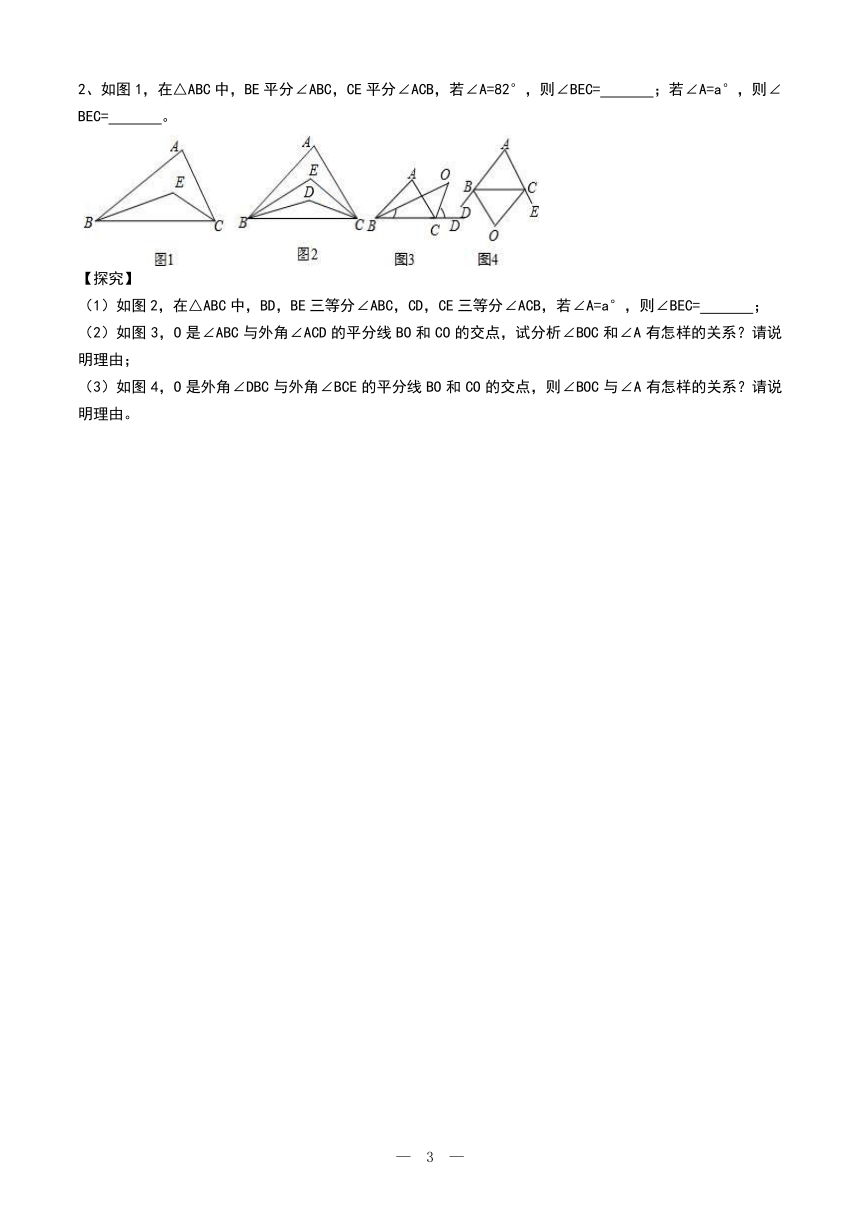
1、在△ABC中,∠A=75°,直线DE交AB于D,交AC于E,则∠BDE+∠CED=( )
A.180° B.215° C.235° D.255°
2、在△ABC中,E、F分别是AB,AC上的点,则∠1+∠2=224°,则∠A=( )
A.17° B.44° C.68° D.无法确定
1题 2题
老鹰捉小鸡模型
结论:∠A+∠BFC=∠DBF+∠FCE,翼下两角之和等于上下两角之和
1、如图,把△ABC沿EF折叠,叠合后的图形如图所示,若∠A=60°,∠1=95,则∠2的度数为( )
A.24°B.25°C.30°D.35°
2、如图,将△ABC纸片沿DE 折叠,点A的对应点为A ,若∠B=60°,∠C=80°,则∠1+∠2 等于( )
A.40°B. 60°C.80°D.140°
1题 2题
五、双角平分线模型结论:
双内角平分线 双外角平分线 内外角平分线
∠D=90°+∠A ∠D=90°-∠A ∠D=∠A
如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;∠A2016BC和∠A2016CD的平分线交于点A2017,求∠A2017的度数____________。
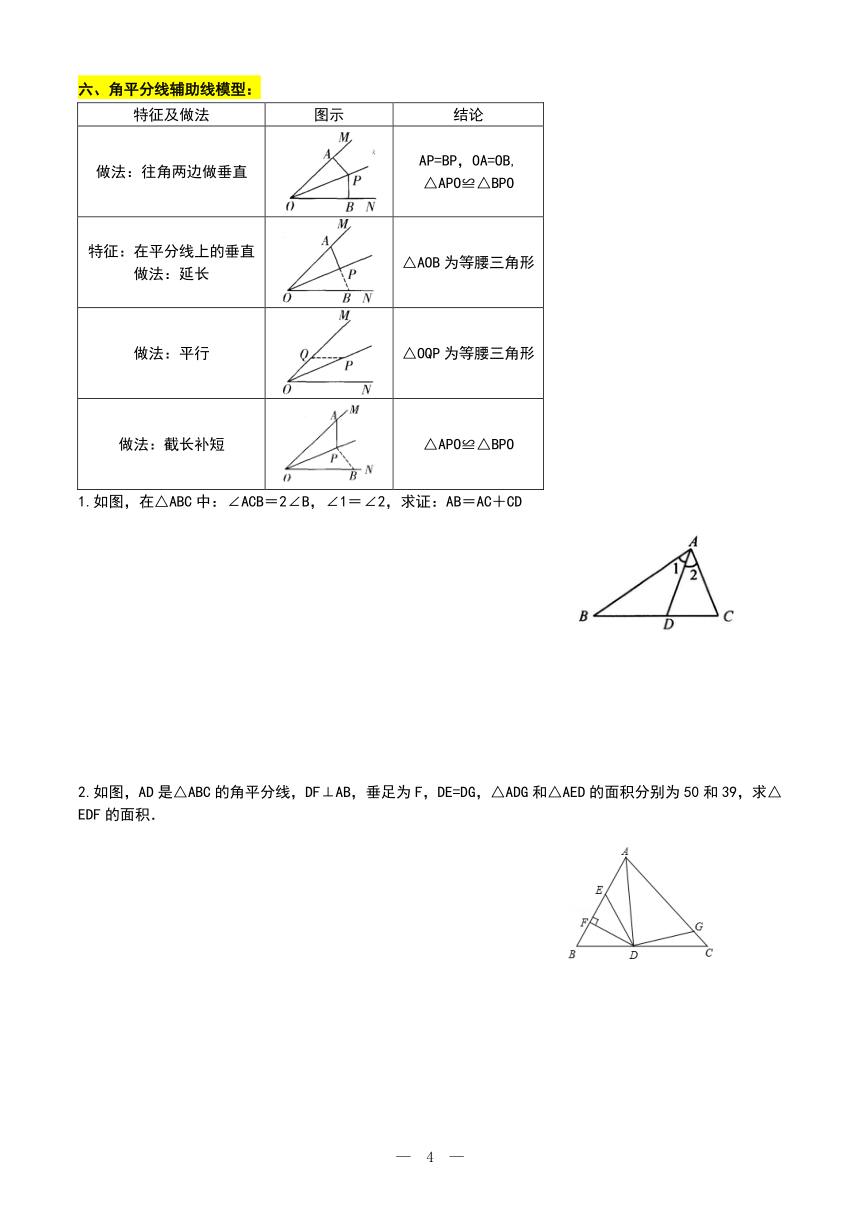
2、如图1,在△ABC中,BE平分∠ABC,CE平分∠ACB,若∠A=82°,则∠BEC= ;若∠A=a°,则∠BEC= 。
【探究】
(1)如图2,在△ABC中,BD,BE三等分∠ABC,CD,CE三等分∠ACB,若∠A=a°,则∠BEC= ;
(2)如图3,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC和∠A有怎样的关系?请说明理由;
(3)如图4,O是外角∠DBC与外角∠BCE的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?请说明理由。
六、角平分线辅助线模型:
特征及做法 图示 结论
做法:往角两边做垂直 AP=BP,OA=OB,△APO≌△BPO
特征:在平分线上的垂直做法:延长 △AOB为等腰三角形
做法:平行 △OQP为等腰三角形
做法:截长补短 △APO≌△BPO
1.如图,在△ABC中:∠ACB=2∠B,∠1=∠2,求证:AB=AC+CD
2.如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和39,求△EDF的面积.
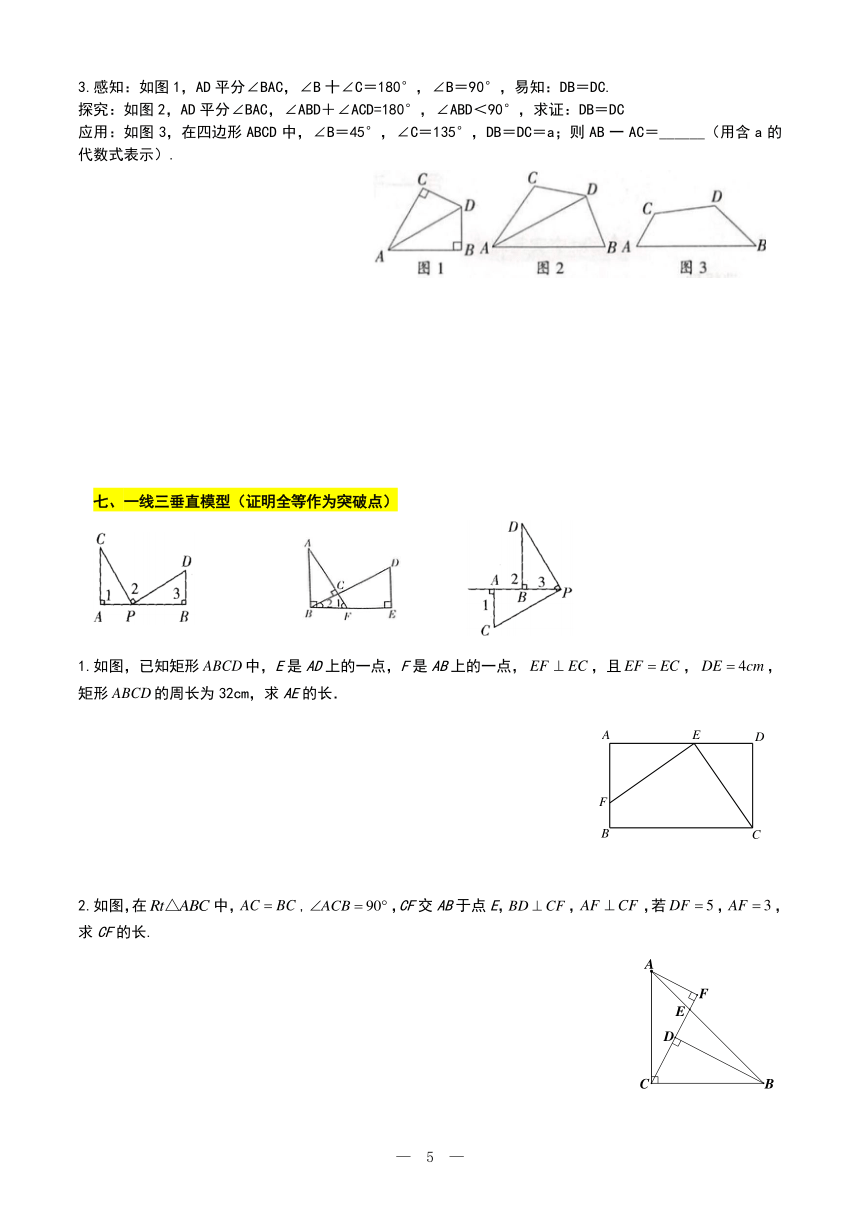
3.感知:如图1,AD平分∠BAC,∠B十∠C=180°,∠B=90°,易知:DB=DC.
探究:如图2,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC
应用:如图3,在四边形ABCD中,∠B=45°,∠C=135°,DB=DC=a;则AB一AC=______(用含a的代数式表示).
一线三垂直模型(证明全等作为突破点)
1.如图,已知矩形中,E是AD上的一点,F是AB上的一点,,且,,矩形的周长为32cm,求AE的长.
2.如图,在中,,,CF交AB于点E,,,若,,求CF的长.
3.在△ABC中, HYPERLINK "https://so1./t018541046cf5835602.png" INCLUDEPICTURE \d "https://so1./t018541046cf5835602.png" \* MERGEFORMATINET , HYPERLINK "https://so1./t01cfd15abf0129b146.png" INCLUDEPICTURE \d "https://so1./t01cfd15abf0129b146.png" \* MERGEFORMATINET ,直线 HYPERLINK "https://so1./t011c320d7a76a66a2f.png" INCLUDEPICTURE \d "https://so1./t011c320d7a76a66a2f.png" \* MERGEFORMATINET 经过点 HYPERLINK "https://so1./t01bcbe236d3844d8a3.png" INCLUDEPICTURE \d "https://so1./t01bcbe236d3844d8a3.png" \* MERGEFORMATINET ,且 HYPERLINK "https://so1./t01e7e7c33e74f6ccc2.png" INCLUDEPICTURE \d "https://so1./t01e7e7c33e74f6ccc2.png" \* MERGEFORMATINET 于 HYPERLINK "https://so1./t013d33c17583aa3653.png" INCLUDEPICTURE \d "https://so1./t013d33c17583aa3653.png" \* MERGEFORMATINET , HYPERLINK "https://so1./t0108779c5c4f1c6199.png" INCLUDEPICTURE \d "https://so1./t0108779c5c4f1c6199.png" \* MERGEFORMATINET 于E.
(1)当直线 HYPERLINK "https://so1./t011c320d7a76a66a2f.png" INCLUDEPICTURE \d "https://so1./t011c320d7a76a66a2f.png" \* MERGEFORMATINET 绕点 HYPERLINK "https://so1./t01bcbe236d3844d8a3.png" INCLUDEPICTURE \d "https://so1./t01bcbe236d3844d8a3.png" \* MERGEFORMATINET 旋转到图1的位置时,求证: ① HYPERLINK "https://so1./t01dae8d1aae5e62c63.png" INCLUDEPICTURE \d "https://so1./t01dae8d1aae5e62c63.png" \* MERGEFORMATINET ≌ HYPERLINK "https://so1./t01c3f3950d9e293d3c.png" INCLUDEPICTURE \d "https://so1./t01c3f3950d9e293d3c.png" \* MERGEFORMATINET ;② HYPERLINK "https://so1./t017f5779b5a247f342.png" INCLUDEPICTURE \d "https://so1./t017f5779b5a247f342.png" \* MERGEFORMATINET .
HYPERLINK "https://so1./t01cd0af55d8062e745.jpg" INCLUDEPICTURE \d "https://so1./t01cd0af55d8062e745.jpg" \* MERGEFORMATINET
(2)当直线 HYPERLINK "https://so1./t0161a71de270fd501a.png" INCLUDEPICTURE \d "https://so1./t0161a71de270fd501a.png" \* MERGEFORMATINET 绕点 HYPERLINK "https://so1./t0141783f5abb185299.png" INCLUDEPICTURE \d "https://so1./t0141783f5abb185299.png" \* MERGEFORMATINET 旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.
HYPERLINK "https://so1./t015471a3fb3a11a510.jpg" INCLUDEPICTURE \d "https://so1./t015471a3fb3a11a510.jpg" \* MERGEFORMATINET
八、“手拉手”全等模型
在直线ABC的同一侧作两个等边三角形△ABD和△BCE,连接AE与CD:
结论:
△ABE≌△DBC
AE=DC
AE与DC的夹角为60。
△AGB≌△DFB
△EGB≌△CFB
BH平分∠AHC
GF∥AC
1、如果两个等边三角形△ABD和△BCE,连接AE与CD,证明:
△ABE≌△DBC
AE=DC
AE与DC的夹角为60。
AE与DC的交点设为H,BH平分∠AHC
2、如果两个等边三角形△ABD和△BCE,连接AE与CD,证明:
(1)△ABE≌△DBC
(2)AE=DC
(3)AE与DC的夹角为60。
(4)AE与DC的交点设为H,BH平分∠AHC
九、将军饮马中四大模型——最短路径问题
题型一 求两条线段和的最小值
题型二 求两条线段差的最大值
题型三 求三条线段和的最小值(双动点问题)
题型四 最值问题的实际应用
【知识梳理】
一 两定点在直线的异侧
问题1 作法 图形 原理
在直线l上找一点P,使得PA+PB的和最小。 连接AB,与直线l的交点P即为所求。 两点之间,线段最短,此时PA+PB的和最小。
二 两定点在直线的同侧
问题2:将军饮马 作法 图形 原理
在直线l上找一点P,使得PA+PB的和最小。 作B关于直线l的对称点C,连AC,与直线l的交点P即为所求。 化折为直;两点之间,线段最短,此时PA+PB的和AC最小。
三 两动点一定点问题
问题3:两个动点 作法 图形 原理
点P在锐角∠AOB的内部,在OA边上找一点C,在OB边上找一点D,使得PC+PD+CD和最小。 作P关于OA的对称点P1,作P关于OB的对称点P2,连接P1P2 。 两点之间,线段最短,此时PC+PD+CD的和最小。
四 造桥选址问题
问题4:造桥选址 作法 图形 原理
直线m∥n,在m,n上分别求点M、N,使MN⊥m,MN⊥n,且AM+MN+BN的和最小。 将点A乡向下平移MN的长度得A1,连A1B,交n于点N,过N作NM⊥m于M。 两点之间,线段最短,此时AM+MN+BN的最小值为A1B+MN。
【题型1:两定一动——作图】
1、(2023 海淀区一模)在一条沿直线铺设的电缆两侧有甲、乙两个小区,现要求在上选取一点P,向两个小区铺设电缆.下面四种铺设方案中,使用电缆材料最少的是( )
A.B.C.D.
【题型2:造桥选址问题】
2、如图,和B两地在一条河的两岸,现要在河上造一座桥MN,使从A到B的路径AMNB最短的是假定河的两岸是平行线,桥与河岸垂直)( )
【题型3:两定一动-求周长/线段和最小值/角度】
3、如图,是等边三角形,D,E分别是边的中点,连接,点P是上一动点,若,则的最小值是( )
A.2B.4C.8D.16
4、如图,直线是中边的垂直平分线,点是直线上的一动点.若,,,则周长的最小值是( )
A.9 B.10 C.10.5 D.11
5、如图,MN是等边三角形ABC的一条对称轴,D为AC的中点,点P是直线MN上的一个动点,当PC+PD最小时,∠PCD的度数是( )
A.30°B.15°C.20°D.35°
【题型4:两动一定-求周长/线段和最小值/角度】
6、如图,点P在∠AOB的内部,点M、N分别是点P关于直线OA、OB的对称点,线段MN交OA,OB于点E,F。
若MN=20cm,求△PEF的周长;
若∠AOB=35°,求∠EPF的度数.
7、如图,四边形ABCD中,∠C=50°,∠B=∠D=90°,E、F分别是BC、DC上的点,当△AEF的周长最小时,求∠EAF的度数
答案解析
一、8字模型
1、∠ACD+∠D=∠A+∠AFE 即∠ACD+30=56+90°,∠ACD=116°,∠ACB=180-116=64°
2、∠A+∠B+∠C+∠D+∠E+∠F等于两个中间三角形的内角和,即360°
3、
二燕尾(飞镖)模型
根据模型,∠1=对顶角=30°+45°+90°=165°
3、∠B+∠F=115°-∠A ∠C+∠E=115°-∠D
∠A+∠B+∠C+∠D+∠E+∠F=∠A+∠D+115°-∠A+115°-∠D=230°
三A字模型
选C ∠BDE+∠CED=180°+∠A=180+75=255
选B ∠A=∠1+∠2-180=224-180=44°
四老鹰捉小鸡模型
选B 延长B’E,C’F交于M,∠1+∠2=∠M+∠A且∠M=∠A,∠2=60+60-95=25°
选C ∠1+∠2=∠A’+∠A=2∠A=2x(180°-60-80)=80°
五、双角平分线模型结论:
1、
2、
六、角平分线辅助线模型:
1、证明:方法1:在AB上取AE=AC,连接DE,∵AE=AC,∠1=∠2,且AD=AD,∴△ACD≌△AED(SAS),∴ED=CD,∠AED=∠C=2∠B,又∵∠AED=∠B+∠BDE,∴∠B=∠BDE,∴EB=ED,即△BED为等腰三角形.∴BE=ED=CD,∴AB=AE+EB=AC
2、
3、
一线三垂直模型
1、
2、
3、解:(1)证明:①∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=90°,
∴∠DAC+∠DCA=∠DCA+∠BCE=90°,
∴∠DAC=∠ECB,
在△ADC和△CEB中,
∠ADC=∠BEC,
∠DAC=∠ECB,
AC=BC,
∴△ADC≌△CEB(AAS);
②∴△ADC≌△CEB
∴AD=CE,CD=BE,
∵DE=CD+CE,
∴DE=AD+BE;
(2)不成立,理由如下,
由(1)可得,同理可证△ADC≌△CEB,
∴CD=BE,AD=CE,
∵DE=CE-CD,
∴DE=AD-BE.
八、手拉手模型
1、
2、
九、将军饮马模型
1.A
【分析】根据两点之间线段最短即可得出答案.
【详解】解:甲、乙位于直线的两侧,
根据两点之间线段最短,连接甲、乙两点,与直线交于点,点即为所求;故选A.
【点睛】本题考查两点之间线段最短的公理,解题的关键是分析题中两点的位置是在直线的同侧还是异侧,在异侧连接两点即可,在同侧需做其中一点的对称点再连接.
2.B
【分析】根据两点之间线段最短、垂线段最短即可得.
【详解】解:由两点之间线段最短、垂线段最短可知,煤炭加工厂到两个村庄路径最短的是:
.
故选:B.
【点睛】本题考查了两点之间线段最短、垂线段最短,熟练掌握两点之间线段最短、垂线段最短是解
3.C
【分析】连接,由对称性知,,则,当P、B、E三点共线时,最小,从而求得最小值.
【详解】解:连接,如图,
由对称性知,,
∴,
当P、B、E三点共线时,最小,最小值为线段的长.
∵是等边三角形,D,E分别是边的中点,
∴,
即的最小值为8;
故选:C.
4.A
【分析】根据垂直平分线的性质,所以周长.
【详解】∵直线m是中边的垂直平分线,
∴
∴周长
∵两点之间线段最短
∴
∴的周长
∵,
∴周长最小为
故选:A
5.C
【分析】作点E关于AD对称的点M,连接CM,与AD交于点F,推出EF+CF最小时即为CM,再根据等边三角形的性质可得结果.
【详解】解:作点E关于AD对称的点M,连接CM,与AD交于点F,
∵△ABC是等边三角形,AD⊥BC,
∴M在AB上,
∴MF=EF,
∴EF+CF=MF+CF=CM,
即此时EF+CF最小,且为CM,
∵AE=2,
∴AM=2,即点M为AB中点,
∴∠ECF=30°,
故选C.
【点睛】本题考查了轴对称最短路线问题,等边三角形的性质,等腰三角形的性质等知识点的应用,找到CM是解题的关键.
6.解:因为点M,N分别是点P关于直线OA,OB的对称点,所以ME=PE,NF=PF.所以PE+EF+PF=ME+EF+NF=MN=20 cm,即△PEF的周长是20 cm.
解:如图,设MP与OA相交于点R,PN与OB相交于点T.
由(1)知ME=PE,PF=NF,所以∠M=∠EPM,∠N=∠FPN.
所以∠PEF=2∠M,∠PFE=2∠N.
因为∠PRE=∠PTF=90°,所以在四边形OTPR中,∠MPN+∠AOB=180°.
因为∠MPN+∠M+∠N=180°,所以∠M+∠N=∠AOB=35°.
所以∠EPF=180°-(∠PEF+∠PFE)=180°-2(∠M+∠N)=180°-35°×2=110°
7.图,作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于E,交CD于F,则A′A″即为△AEF的周长的最小值.连接AC
因为∠ABC+∠BCA+∠BAC=180°,∠ADC+∠DCA+∠DAC=180°,∠ABC=90°,∠ADC=90°,∠BCA+∠DCA=50°,
所以∠BAC+∠DAC=130°,即∠DAB=130°.
所以∠A′+∠A″=180°-∠DAB=50°.
因为∠A′=∠EAA′,∠FAD=∠A″,
所以∠EAA′+∠A″AF=50°.
所以∠EAF=130°-50°=80°
一、8字模型
结论:①∠A+∠B=∠C+∠D;②AB+CD<AD+BC
斜8字型(蝴蝶型) 燕尾型
1、如图,已知D是△ABC的BC边的延长线上一点,DF⊥AB,交AB于点F,交AC于点E,∠A=56°,∠D=30°,则∠ACB的度数为_________
2、如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为_________
3、求:∠CAD+∠B+∠C+∠D+∠E=_________
1题 2题 3题
燕尾(飞镖)模型
结论:∠BDC=∠A+∠B+∠C
1、将一副直角三角板如图放置,使两直角边重合,则∠1的度数为__________
2、如图,是一块不规则的纸片,∠ABC=∠DEF=80°,则∠A+∠C+∠D+∠F的度数为__________
3、如图,求∠A+∠B+∠C+∠D+∠E+∠F= .
1题 2题 3题
A字模型
结论:∠DBC+∠ECB=180°+∠A
1、在△ABC中,∠A=75°,直线DE交AB于D,交AC于E,则∠BDE+∠CED=( )
A.180° B.215° C.235° D.255°
2、在△ABC中,E、F分别是AB,AC上的点,则∠1+∠2=224°,则∠A=( )
A.17° B.44° C.68° D.无法确定
1题 2题
老鹰捉小鸡模型
结论:∠A+∠BFC=∠DBF+∠FCE,翼下两角之和等于上下两角之和
1、如图,把△ABC沿EF折叠,叠合后的图形如图所示,若∠A=60°,∠1=95,则∠2的度数为( )
A.24°B.25°C.30°D.35°
2、如图,将△ABC纸片沿DE 折叠,点A的对应点为A ,若∠B=60°,∠C=80°,则∠1+∠2 等于( )
A.40°B. 60°C.80°D.140°
1题 2题
五、双角平分线模型结论:
双内角平分线 双外角平分线 内外角平分线
∠D=90°+∠A ∠D=90°-∠A ∠D=∠A
如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;∠A2016BC和∠A2016CD的平分线交于点A2017,求∠A2017的度数____________。
2、如图1,在△ABC中,BE平分∠ABC,CE平分∠ACB,若∠A=82°,则∠BEC= ;若∠A=a°,则∠BEC= 。
【探究】
(1)如图2,在△ABC中,BD,BE三等分∠ABC,CD,CE三等分∠ACB,若∠A=a°,则∠BEC= ;
(2)如图3,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC和∠A有怎样的关系?请说明理由;
(3)如图4,O是外角∠DBC与外角∠BCE的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?请说明理由。
六、角平分线辅助线模型:
特征及做法 图示 结论
做法:往角两边做垂直 AP=BP,OA=OB,△APO≌△BPO
特征:在平分线上的垂直做法:延长 △AOB为等腰三角形
做法:平行 △OQP为等腰三角形
做法:截长补短 △APO≌△BPO
1.如图,在△ABC中:∠ACB=2∠B,∠1=∠2,求证:AB=AC+CD
2.如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和39,求△EDF的面积.
3.感知:如图1,AD平分∠BAC,∠B十∠C=180°,∠B=90°,易知:DB=DC.
探究:如图2,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC
应用:如图3,在四边形ABCD中,∠B=45°,∠C=135°,DB=DC=a;则AB一AC=______(用含a的代数式表示).
一线三垂直模型(证明全等作为突破点)
1.如图,已知矩形中,E是AD上的一点,F是AB上的一点,,且,,矩形的周长为32cm,求AE的长.
2.如图,在中,,,CF交AB于点E,,,若,,求CF的长.
3.在△ABC中, HYPERLINK "https://so1./t018541046cf5835602.png" INCLUDEPICTURE \d "https://so1./t018541046cf5835602.png" \* MERGEFORMATINET , HYPERLINK "https://so1./t01cfd15abf0129b146.png" INCLUDEPICTURE \d "https://so1./t01cfd15abf0129b146.png" \* MERGEFORMATINET ,直线 HYPERLINK "https://so1./t011c320d7a76a66a2f.png" INCLUDEPICTURE \d "https://so1./t011c320d7a76a66a2f.png" \* MERGEFORMATINET 经过点 HYPERLINK "https://so1./t01bcbe236d3844d8a3.png" INCLUDEPICTURE \d "https://so1./t01bcbe236d3844d8a3.png" \* MERGEFORMATINET ,且 HYPERLINK "https://so1./t01e7e7c33e74f6ccc2.png" INCLUDEPICTURE \d "https://so1./t01e7e7c33e74f6ccc2.png" \* MERGEFORMATINET 于 HYPERLINK "https://so1./t013d33c17583aa3653.png" INCLUDEPICTURE \d "https://so1./t013d33c17583aa3653.png" \* MERGEFORMATINET , HYPERLINK "https://so1./t0108779c5c4f1c6199.png" INCLUDEPICTURE \d "https://so1./t0108779c5c4f1c6199.png" \* MERGEFORMATINET 于E.
(1)当直线 HYPERLINK "https://so1./t011c320d7a76a66a2f.png" INCLUDEPICTURE \d "https://so1./t011c320d7a76a66a2f.png" \* MERGEFORMATINET 绕点 HYPERLINK "https://so1./t01bcbe236d3844d8a3.png" INCLUDEPICTURE \d "https://so1./t01bcbe236d3844d8a3.png" \* MERGEFORMATINET 旋转到图1的位置时,求证: ① HYPERLINK "https://so1./t01dae8d1aae5e62c63.png" INCLUDEPICTURE \d "https://so1./t01dae8d1aae5e62c63.png" \* MERGEFORMATINET ≌ HYPERLINK "https://so1./t01c3f3950d9e293d3c.png" INCLUDEPICTURE \d "https://so1./t01c3f3950d9e293d3c.png" \* MERGEFORMATINET ;② HYPERLINK "https://so1./t017f5779b5a247f342.png" INCLUDEPICTURE \d "https://so1./t017f5779b5a247f342.png" \* MERGEFORMATINET .
HYPERLINK "https://so1./t01cd0af55d8062e745.jpg" INCLUDEPICTURE \d "https://so1./t01cd0af55d8062e745.jpg" \* MERGEFORMATINET
(2)当直线 HYPERLINK "https://so1./t0161a71de270fd501a.png" INCLUDEPICTURE \d "https://so1./t0161a71de270fd501a.png" \* MERGEFORMATINET 绕点 HYPERLINK "https://so1./t0141783f5abb185299.png" INCLUDEPICTURE \d "https://so1./t0141783f5abb185299.png" \* MERGEFORMATINET 旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.
HYPERLINK "https://so1./t015471a3fb3a11a510.jpg" INCLUDEPICTURE \d "https://so1./t015471a3fb3a11a510.jpg" \* MERGEFORMATINET
八、“手拉手”全等模型
在直线ABC的同一侧作两个等边三角形△ABD和△BCE,连接AE与CD:
结论:
△ABE≌△DBC
AE=DC
AE与DC的夹角为60。
△AGB≌△DFB
△EGB≌△CFB
BH平分∠AHC
GF∥AC
1、如果两个等边三角形△ABD和△BCE,连接AE与CD,证明:
△ABE≌△DBC
AE=DC
AE与DC的夹角为60。
AE与DC的交点设为H,BH平分∠AHC
2、如果两个等边三角形△ABD和△BCE,连接AE与CD,证明:
(1)△ABE≌△DBC
(2)AE=DC
(3)AE与DC的夹角为60。
(4)AE与DC的交点设为H,BH平分∠AHC
九、将军饮马中四大模型——最短路径问题
题型一 求两条线段和的最小值
题型二 求两条线段差的最大值
题型三 求三条线段和的最小值(双动点问题)
题型四 最值问题的实际应用
【知识梳理】
一 两定点在直线的异侧
问题1 作法 图形 原理
在直线l上找一点P,使得PA+PB的和最小。 连接AB,与直线l的交点P即为所求。 两点之间,线段最短,此时PA+PB的和最小。
二 两定点在直线的同侧
问题2:将军饮马 作法 图形 原理
在直线l上找一点P,使得PA+PB的和最小。 作B关于直线l的对称点C,连AC,与直线l的交点P即为所求。 化折为直;两点之间,线段最短,此时PA+PB的和AC最小。
三 两动点一定点问题
问题3:两个动点 作法 图形 原理
点P在锐角∠AOB的内部,在OA边上找一点C,在OB边上找一点D,使得PC+PD+CD和最小。 作P关于OA的对称点P1,作P关于OB的对称点P2,连接P1P2 。 两点之间,线段最短,此时PC+PD+CD的和最小。
四 造桥选址问题
问题4:造桥选址 作法 图形 原理
直线m∥n,在m,n上分别求点M、N,使MN⊥m,MN⊥n,且AM+MN+BN的和最小。 将点A乡向下平移MN的长度得A1,连A1B,交n于点N,过N作NM⊥m于M。 两点之间,线段最短,此时AM+MN+BN的最小值为A1B+MN。
【题型1:两定一动——作图】
1、(2023 海淀区一模)在一条沿直线铺设的电缆两侧有甲、乙两个小区,现要求在上选取一点P,向两个小区铺设电缆.下面四种铺设方案中,使用电缆材料最少的是( )
A.B.C.D.
【题型2:造桥选址问题】
2、如图,和B两地在一条河的两岸,现要在河上造一座桥MN,使从A到B的路径AMNB最短的是假定河的两岸是平行线,桥与河岸垂直)( )
【题型3:两定一动-求周长/线段和最小值/角度】
3、如图,是等边三角形,D,E分别是边的中点,连接,点P是上一动点,若,则的最小值是( )
A.2B.4C.8D.16
4、如图,直线是中边的垂直平分线,点是直线上的一动点.若,,,则周长的最小值是( )
A.9 B.10 C.10.5 D.11
5、如图,MN是等边三角形ABC的一条对称轴,D为AC的中点,点P是直线MN上的一个动点,当PC+PD最小时,∠PCD的度数是( )
A.30°B.15°C.20°D.35°
【题型4:两动一定-求周长/线段和最小值/角度】
6、如图,点P在∠AOB的内部,点M、N分别是点P关于直线OA、OB的对称点,线段MN交OA,OB于点E,F。
若MN=20cm,求△PEF的周长;
若∠AOB=35°,求∠EPF的度数.
7、如图,四边形ABCD中,∠C=50°,∠B=∠D=90°,E、F分别是BC、DC上的点,当△AEF的周长最小时,求∠EAF的度数
答案解析
一、8字模型
1、∠ACD+∠D=∠A+∠AFE 即∠ACD+30=56+90°,∠ACD=116°,∠ACB=180-116=64°
2、∠A+∠B+∠C+∠D+∠E+∠F等于两个中间三角形的内角和,即360°
3、
二燕尾(飞镖)模型
根据模型,∠1=对顶角=30°+45°+90°=165°
3、∠B+∠F=115°-∠A ∠C+∠E=115°-∠D
∠A+∠B+∠C+∠D+∠E+∠F=∠A+∠D+115°-∠A+115°-∠D=230°
三A字模型
选C ∠BDE+∠CED=180°+∠A=180+75=255
选B ∠A=∠1+∠2-180=224-180=44°
四老鹰捉小鸡模型
选B 延长B’E,C’F交于M,∠1+∠2=∠M+∠A且∠M=∠A,∠2=60+60-95=25°
选C ∠1+∠2=∠A’+∠A=2∠A=2x(180°-60-80)=80°
五、双角平分线模型结论:
1、
2、
六、角平分线辅助线模型:
1、证明:方法1:在AB上取AE=AC,连接DE,∵AE=AC,∠1=∠2,且AD=AD,∴△ACD≌△AED(SAS),∴ED=CD,∠AED=∠C=2∠B,又∵∠AED=∠B+∠BDE,∴∠B=∠BDE,∴EB=ED,即△BED为等腰三角形.∴BE=ED=CD,∴AB=AE+EB=AC
2、
3、
一线三垂直模型
1、
2、
3、解:(1)证明:①∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=90°,
∴∠DAC+∠DCA=∠DCA+∠BCE=90°,
∴∠DAC=∠ECB,
在△ADC和△CEB中,
∠ADC=∠BEC,
∠DAC=∠ECB,
AC=BC,
∴△ADC≌△CEB(AAS);
②∴△ADC≌△CEB
∴AD=CE,CD=BE,
∵DE=CD+CE,
∴DE=AD+BE;
(2)不成立,理由如下,
由(1)可得,同理可证△ADC≌△CEB,
∴CD=BE,AD=CE,
∵DE=CE-CD,
∴DE=AD-BE.
八、手拉手模型
1、
2、
九、将军饮马模型
1.A
【分析】根据两点之间线段最短即可得出答案.
【详解】解:甲、乙位于直线的两侧,
根据两点之间线段最短,连接甲、乙两点,与直线交于点,点即为所求;故选A.
【点睛】本题考查两点之间线段最短的公理,解题的关键是分析题中两点的位置是在直线的同侧还是异侧,在异侧连接两点即可,在同侧需做其中一点的对称点再连接.
2.B
【分析】根据两点之间线段最短、垂线段最短即可得.
【详解】解:由两点之间线段最短、垂线段最短可知,煤炭加工厂到两个村庄路径最短的是:
.
故选:B.
【点睛】本题考查了两点之间线段最短、垂线段最短,熟练掌握两点之间线段最短、垂线段最短是解
3.C
【分析】连接,由对称性知,,则,当P、B、E三点共线时,最小,从而求得最小值.
【详解】解:连接,如图,
由对称性知,,
∴,
当P、B、E三点共线时,最小,最小值为线段的长.
∵是等边三角形,D,E分别是边的中点,
∴,
即的最小值为8;
故选:C.
4.A
【分析】根据垂直平分线的性质,所以周长.
【详解】∵直线m是中边的垂直平分线,
∴
∴周长
∵两点之间线段最短
∴
∴的周长
∵,
∴周长最小为
故选:A
5.C
【分析】作点E关于AD对称的点M,连接CM,与AD交于点F,推出EF+CF最小时即为CM,再根据等边三角形的性质可得结果.
【详解】解:作点E关于AD对称的点M,连接CM,与AD交于点F,
∵△ABC是等边三角形,AD⊥BC,
∴M在AB上,
∴MF=EF,
∴EF+CF=MF+CF=CM,
即此时EF+CF最小,且为CM,
∵AE=2,
∴AM=2,即点M为AB中点,
∴∠ECF=30°,
故选C.
【点睛】本题考查了轴对称最短路线问题,等边三角形的性质,等腰三角形的性质等知识点的应用,找到CM是解题的关键.
6.解:因为点M,N分别是点P关于直线OA,OB的对称点,所以ME=PE,NF=PF.所以PE+EF+PF=ME+EF+NF=MN=20 cm,即△PEF的周长是20 cm.
解:如图,设MP与OA相交于点R,PN与OB相交于点T.
由(1)知ME=PE,PF=NF,所以∠M=∠EPM,∠N=∠FPN.
所以∠PEF=2∠M,∠PFE=2∠N.
因为∠PRE=∠PTF=90°,所以在四边形OTPR中,∠MPN+∠AOB=180°.
因为∠MPN+∠M+∠N=180°,所以∠M+∠N=∠AOB=35°.
所以∠EPF=180°-(∠PEF+∠PFE)=180°-2(∠M+∠N)=180°-35°×2=110°
7.图,作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于E,交CD于F,则A′A″即为△AEF的周长的最小值.连接AC
因为∠ABC+∠BCA+∠BAC=180°,∠ADC+∠DCA+∠DAC=180°,∠ABC=90°,∠ADC=90°,∠BCA+∠DCA=50°,
所以∠BAC+∠DAC=130°,即∠DAB=130°.
所以∠A′+∠A″=180°-∠DAB=50°.
因为∠A′=∠EAA′,∠FAD=∠A″,
所以∠EAA′+∠A″AF=50°.
所以∠EAF=130°-50°=80°
同课章节目录
